下载文档原格式
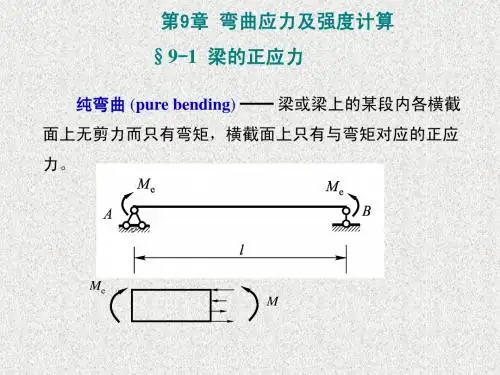
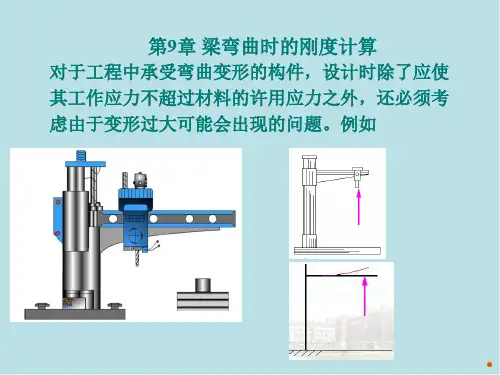
第9章弯曲刚度问题9.1 基本概念9.1.1 梁弯曲后的挠曲线吊车梁若变形过大，将使小车行走困难，还会引起梁的严重振动。
因此，必须对梁的变形加以限制若梁的变形在弹性范围内，梁的轴线在梁弯曲后变为一条连续光滑曲线，该曲线称为弹性曲线或挠度曲线，简称弹性线或挠曲线。
挠曲线：梁变形后的轴线。
性质：连续、光滑、弹性、极其平坦的平面曲线。
9.1.2梁的挠度与转角设有一具有纵向对称面的悬臂梁，在自由端处作用一集中力F p。
F p力作用在梁的纵向对称面内，使梁发生平面弯曲。
一、挠度与转角梁的变形可用以下两个基本量来度量。
tan"二dw ,、w(x)二 w ‘ dxtan0-W⑴挠度挠度：横截面形心沿垂直于轴线方向的位移梁轴线上各点（各截面）的挠度w 随着点（截面）的位置 x 的不同而改变，即各截面的挠度是截面位置坐标x 的函数。
因小变形时，u 与w 相比为高阶无穷小，故忽略不计。
、挠度w 于转角二间的关系w = w(x)d挠曲线方程 单位：mm挠度 w 符号规定：向下为正⑵转角，向上为负。
转角：横截面绕中性轴转过的角度。
用“，”表示。
梁不同横截面其转角是不相同的，二是横截面位置坐标x 的函数 6 = &(兀)转角方程 单位：rad71的符号规定：由变形前的横截面转到变形后，顺时针为正；逆时针为负。
⑶ 水平位移：横截面形心沿水平方向的位移，用 u 表示。
9.2 小挠度微分方程及其积分9.2.1 小挠度微分方程1梁发生平面弯曲时，其轴线由直线变成一条曲率为7的平面曲线1 M 1 M (x)纯弯曲EI细长梁横力弯曲(x) El12d w d2w M(x)2dx2El 由高数知(x)dxM (x)与W的符号总是相反的JElM (x)dx C _______ 转角方程dw w解上二阶微分方程可求得挠度 w ，再根据dx，可求得截面转角71。
等截面梁：EI =常数。
Elw …M (x) Elw dx …M (x)dxElw = El — - 严(x)dx C Elw dx 二[j M (x)dx]dx Cdx Elw 二 」| M (x)dx]dx Cx Dd 2w M (x) dx 2 El尸EIw” = -M (工)求梁的变形：d 2w Eldx 2-M (x)挠曲线近似微分方程1 5 / 28w[ M (x)dx]dx Cx DE| i i ''____ 挠度方程其中C 、D 为积分常数。
工程力学中的弯曲刚度与刚度优化设计工程力学中的弯曲刚度是指材料、结构或系统在受到弯曲作用时的抵抗变形的能力。
弯曲刚度是工程设计中非常重要的一个参数，影响着结构的稳定性、安全性和使用寿命。
本文将详细介绍工程力学中的弯曲刚度的概念、计算方法以及刚度优化设计的应用。
一、弯曲刚度的概念与计算方法1. 弯曲刚度的概念弯曲刚度是指材料或结构在受到弯曲作用时所表现出的抵抗变形的能力。
一般来说，弯曲刚度可以通过弯曲刚度系数（bending stiffness）来表示，它是弯曲力矩对应的曲率和截面惯性矩的比值。
2. 弯曲刚度的计算方法计算弯曲刚度的方法根据不同的工程问题和结构类型而有所不同。
对于一维梁的弯曲刚度计算，可以使用梁的基本弯曲理论，根据梁的几何形状、材料的力学性质以及施加载荷的形式进行计算。
对于复杂的结构或系统，可以使用有限元分析等数值方法进行计算。
二、刚度优化设计的概念与方法1. 刚度优化设计的概念刚度优化设计是指在满足工程要求的前提下，通过合理设计结构的尺寸和布局，以提高结构的弯曲刚度。
刚度优化设计可以使结构在承受荷载时变形较小，增强结构的稳定性和抗震性能，提高结构的使用寿命。
2. 刚度优化设计的方法刚度优化设计的方法分为直接优化方法和参数化优化方法两种。
直接优化方法主要是通过对结构的形状、截面和材料等进行优化，以提高结构的弯曲刚度。
参数化优化方法则是通过对结构的参数进行调整，以实现刚度的优化设计。
常用的优化算法有遗传算法、蚁群算法等。
三、刚度优化设计的应用案例1. 建筑结构的刚度优化设计在建筑结构设计中，刚度优化设计可以减少结构的变形和振动，提高结构的整体稳定性和抗震性能。
通过对结构的布局、尺寸和材料等进行优化，可以达到节约材料、降低成本的效果。
2. 机械结构的刚度优化设计在机械结构设计中，刚度优化设计可以提高机械系统的精度和稳定性，减少机械运动过程中的变形和振动。
通过优化机械结构的刚度，可以提高机械系统的工作效率和使用寿命。
