工程力学-第9章习题课共48页文档
- 格式:ppt
- 大小:4.26 MB
- 文档页数:24


工程力学第9章答案第9章弹性杆件横截面上的切应力分析9-1 扭转切应力公式p /)(I M x ρρτ=的应用范围有以下几种,试判断哪一种是正确的。
(A )等截面圆轴,弹性范围内加载;(B )等截面圆轴;(C )等截面圆轴与椭圆轴;(D )等截面圆轴与椭圆轴,弹性范围内加载。
正确答案是 A 。
解:p )(I M x ρρτ=在推导时利用了等截面圆轴受扭后,其横截面保持平面的假设,同时推导过程中还应用了剪切胡克定律,要求在线弹性范围加载。
9-2 两根长度相等、直径不等的圆轴承受相同的扭矩受扭后,轴表面上母线转过相同的角度。
设直径大的轴和直径小的轴的横截面上的最大切应力分别为max 1τ和max 2τ,切变模量分别为G 1和G 2。
试判断下列结论的正确性。
(A )max 1τ>max 2τ;(B )max 1τ<max 2τ;(C )若G 1>G 2,则有max 1τ>max 2τ;(D )若G 1>G 2,则有max 1τ<max 2τ。
正确答案是 C 。
解:因两圆轴等长,轴表面上母线转过相同角度,指切应变相同,即γγγ==21由剪切胡克定律γτG =知21G G >时,max 2max 1ττ>。
9-3 承受相同扭矩且长度相等的直径为d 1的实心圆轴与内、外径分别为d 2、)/(222D d D =α的空心圆轴,二者横截面上的最大切应力相等。
关于二者重之比(W 1/W 2)有如下结论,试判断哪一种是正确的。
(A )234)1(α-;(B ))1()1(234αα--;(C ))1)(1(24αα--;(D ))1/()1(2324αα--。
正确答案是 D 。
解:由max 2max1ττ=得)1(π16π1643231α-=D M d M xx即31421)1(α-=D d(1))1(222212121α-==D d A A W W (2)(1)代入(2),得2324211)1(αα--=W W9-4 由两种不同材料组成的圆轴,里层和外层材料的切变模量分别为G 1和G 2,且G 1 = 2G 2。







第9章平面体系的几何组成分析习题.【解】若上部结构与地基之间的连接比较多(N4),能够考虑先将上部结构中的某•刚片与地基连成一个大刚片。
然后,在考虑这个大刚片与上部其它杆件的连接。
本例中,上部结构与地基之间用4个约束连接。
杆件ABE与地基之间用钗A和一根不同过该絞的链杆B相连,组成几何不变体系,且没有多余约束。
所以,能够将杆件ABE与地基看成一个没有多余约束的大刚片。
杆件FCD用三根既不相互平行又不相交于一点的链杆(链杆EF、链杆C、链杆D)与这个大刚片相连,组成一个更大的几何不变体系,且没有多余约束。
杆件ABE与地基之间用平行链杆A和一根不同过该絞的链杆B相连,组成几何不变体系,且没有多余约束。
将杆件ABE与地基看成一个没有多余约束的大刚片。
杆件FCD用三根既不相互平行又不相交于一点的链杆(链杆EF、链杆C、链杆D)与这个大刚片相连,组成一个更大的几何不变体系,且没有多余约束。
-I*羡诊为习题(C)图若上部结构中有皎接三角形,能够考虑将这些三角形看成刚片,然后在进行分析。
刚片I与地基组成•个没有多余约束的大刚片。
这个大刚片与刚片II用三根既不相互平行又不相交于一点的链杆相连,组成一个更大的几何不变体系,且没有多余约束。
习题(d)图将扩大的三角形看成刚片。
先分析一部分:左边的刚片与地基组成一个大刚片ABCD。
增加二元体:在大刚片ABCD上增加二元体DE杆和链杆E,组成一个更大的刚片。
此刚片与刚片GH1F由三根延长线交于H点的链杆(杆件CG、杆件FE、链杆1)相连。
故,体系为瞬变体系。
若上部结构与地基之间用三个约束连接,且符合几何不变体系的组成规律,能够只分析上部结构。
上部结构的分析结论就是整个体系的分析结论。
若折杆只用两个较与其它物体相连,能够将折杆看成是连接两个钗的直杆。
去掉二元体。
剩下部分为两个刚片用两个钗连接,为几何不变体系,且有一个多余约束。
故,整体体系也为几何不变体系,且有一个多余约束。
第九章刚体的平面运动第一节刚体平面运动的概述和运动分解教学时数:1学时教学目标:1、明确刚体平面运动的特征2、掌握研究平面运动的方法3、能够正确判断机构中作平面运动的刚体教学重点:掌握研究平面运动的方法教学难点:掌握研究平面运动的方法教学方法:板书+PowerPoint一.平面运动的概念引例1:汽车沿直线行驶时,车轮的运动(图10.1)车轮的运动随着车身的平动+相对车身的转动。
引例2.曲柄连杆机构的连杆AB的运动引例3.板擦在黑板上的任意运动上述运动有何共性?平面运动定义:刚体运动时其上任一点到某一固定平面的距离始终保持不变,也就是说刚体内的各点都在平行于固定平面的某一平面内运动。
2.力学模型简化如图所示,刚体作平面运动时,刚体上所有与空间某固定平面距离相等的点所构成的平面图形就保持在它自身所在的平面内运动。
A 点代表21A A 线段的运动 B 点代表21B B 线段的运动 平面图形S 代表刚体运动结论:刚体的平面运动可以简化为平面图形在其自身平面内的运动。
3、运动方程确定平面图形S 在Oxy 坐标系内的位置只需确定任一线段AB 在Oxy 中的位置确定AB 线段的位置,需确定坐标),,(ϕA A y x ,,A 点称为基点。
所以平面运动的运动方程:)()()(t t y y t x x A A A A A ϕϕ=== (1)上式称为刚体的平面运动方程。
分析运动方程可知,平面运动包函了平动和定轴转动这两种基本运动形式,即:平面运动是平动和转动的合成运动。
4、运动的分解及分解运动的特性分析特例分析:在方程(1)中,若C =ϕ则“S ”作平动 ,若⎩⎨⎧==21C y C x AA 则“S ”作定轴转动一般情况下,平面运动可以看成为由平动和定轴转动的合成。
运动分解:研究对象:平面图形S 静系:固定平面Oxy 。
动系:y x A ''(其中A 是“S ”上一点,y x A ''伴随A 作平动,是虚构的一坐标系)。
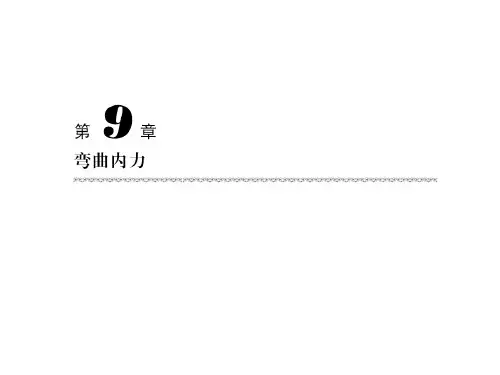
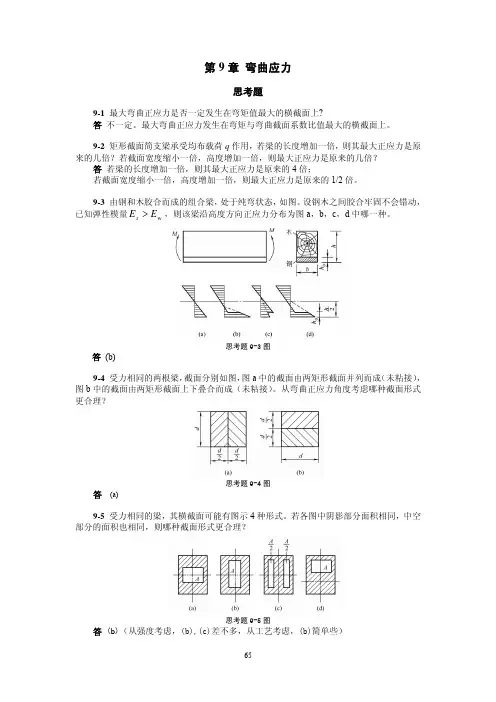
习题9-1图 (b-1)(a-1) 习题9-2图 习题9-2图(a)第9章 应力状态分析9-1 木制构件中的微元受力如图所示,其中所示的角度为木纹方向与铅垂方向的夹角。
试求: 1.面内平行于木纹方向的切应力;2.垂直于木纹方向的正应力。
解:(a )平行于木纹方向切应力 6.0))15(2cos(0))15(2sin(2)6.1(4=︒-⨯⋅+︒-⨯---=''y x τMPa垂直于木纹方向正应力84.30))15(2cos(2)6.1(42)6.1(4-=+︒-⨯---+-+-='x σMPa(b )切应力08.1))15(2cos(25.1-=︒-⨯-=''y x τMPa 正应力625.0))15(2sin()25.1(-=︒-⨯--='x σMPa9-2 层合板构件中微元受力如图所示,各层板之间用胶粘接,接缝方向如图中所示。
若已知胶层切应力不得超过1MPa 。
试分析是否满足这一要求。
解:55.1))60(2cos(5.0))60(2sin(2)1(2-=︒-⨯⋅+︒-⨯---=''y x τMPa 1MPa 55.1||>=''y x τMPa ,不满足。
9-3 结构中某点处的应力状态为两种应力状态的叠加结果。
试求叠加后所得应力状态的主应力、面内最大切应力和该点处的最大切应力。
解:左微元⎪⎪⎪⎩⎪⎪⎪⎨⎧-='-='-=-='+=--+='000000022cos 122sin )2sin(222cos 10)2cos(22σθσσσσθθστσθθσσσx yxyx叠加 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+'=-=+=+=+'=''000022c o s 1022s i n 022c o s 3σθσσσθττσθσσσy y y x xy x x 面内最大切应力:θσσστcos 2021max=-=' 该点最大切应力:031max 2cos 12σθσστ+=-= 左微元0023))30(2sin()(ττσ=︒-⨯-='x ,0230τσσ-='-='x y ,2))30(2cos(00τττ=︒-⨯='xy 右微元0023)302sin()(ττσ=︒⨯-=''x,0230τσσ-=''-=''xy ,2))30(2cos()(00τττ-=︒⨯-=''xy 叠加 03τσσσ='+'=y x x ,03τσσσ-=''+'=yy y ,0=''+'=xy xy xy τττ 013τσ=,02=σ,033τσ-= 面内031max32||τσστ=-='该点031max32||τσστ=-=(a) (a) 习题9-6图习题9-4图 (a)习题9-5图(a)习题9-7图 习题9-7解图习题9-8图 (a) (b) 习题9-9图 (c)(c)叠加[]⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡︒-⨯--+==--+==⎥⎦⎤⎢⎣⎡︒-⨯--+-++=MPa 30))45(2sin(2)30(5070MPa 1010)3050(0MPa 90))45(2cos(2)30(502)30(5080xy y x σσσ主应力0MPa 0MPa100304)]100(90[212109022231=⎩⎨⎧=⨯+-±+=⎭⎬⎫σσσ面内及该点:5021002||||31max max=-=-=='σσττMPa9-4 已知平面应力状态的最大正应力发生在与外力作用的自由表面AB 相垂直的面上,其值为0σ。