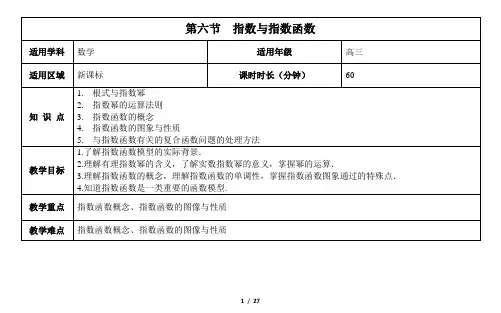
指数与指数函数(教案)
- 格式:docx
- 大小:408.19 KB
- 文档页数:11

《指数函数》的优秀教案最新9篇高一数学《指数函数》优秀教案篇一我本节课说课的内容是高中数学第一册第二章第六节“指数函数”的第一课时——指数函数的定义,图像及性质。
我将尝试运用新课标的理念指导本节课的教学。
新课标指出,学生是教学的主体,教师的教要应本着从学生的认知规律出发,以学生活动为主线,在原有知识的基础上,建构新的知识体系。
我将以此为基础从教材分析,教学目标分析,教法学法分析和教学过程分析这几个方面加以说明。
一、教材分析1、教材的地位和作用:函数是高中数学学习的重点和难点,函数的贯穿于整个高中数学之中。
本节课是学生在已掌握了函数的一般性质和简单的指数运算的基础上,进一步研究指数函数,以及指数函数的图像与性质,同时也为今后研究对数函数以及等比数列的性质打下坚实的基础。
因此,本节课的内容十分重要,它对知识起到了承上启下的作用。
2、教学的重点和难点:根据这一节课的内容特点以及学生的实际情况,我将本节课教学重点定为指数函数的图像、性质及其运用,本节课的难点是指数函数图像和性质的发现过程,及指数函数图像与底的关系。
二、教学目标分析基于对教材的理解和分析,我制定了以下的教学目标:1、知识目标(直接性目标):理解指数函数的定义,掌握指数函数的图像、性质及其简单应用。
2、能力目标(发展性目标):通过教学培养学生观察、分析、归纳等思维能力,体会数形结合和分类讨论,增强学生识图用图的'能力。
3、情感目标(可持续性目标):通过学习,使学生学会认识事物的特殊性与一般性之间的关系,培养学生勇于提问,善于探索的思维品质。
三、教法学法分析1、教学策略:首先从实际问题出发,激发学生的学习兴趣。
第二步,学生归纳指数的图像和性质。
第三步,典型例题分析,加深学生对指数函数的理解。
2、教学:贯彻引导发现式教学原则,在教学中既注重知识的直观素材和背景材料,又要激活相关知识和引导学生思考、探究、创设有趣的问题。
3、教法分析:根据教学内容和学生的状况,本节课我采用引导发现式的教学方法并充分利用多媒体辅助教学。
教学过程一、课堂导入英国的马尔萨斯曾提出“人口增长模型”。
他指出,如果人口按照指数函数的规律增长,那么100年后地球上的每个人肩上都会站着一个人。
“人口按指数增长会有那么快吗?指数函数是怎样的函数二、复习预习1.二次函数的图像与性质2.二次函数在闭区间上的最值3.二次函数、一元二次方程、一元二次不等式的关系4.幂函数的概念、幂函数的图象和性质三、知识讲解考点1 根式(1)根式的概念:(2)两个重要公式:①na n=⎩⎪⎨⎪⎧a,n为奇数,|a|=⎩⎨⎧a(a≥0),-a(a<0),n为偶数;②(na)n=a(注意a必须使na有意义).考点2 有理数指数幂(1)幂的有关概念:①正分数指数幂:a mn=na m(a>0,m,n∈N*,且n>1);②负分数指数幂:amn=1amn=1na m(a>0,m,n∈N*,且n>1);③0的正分数指数幂等于0,0的负分数指数幂无意义.(2)有理数指数幂的性质:①a r a s=a r+s(a>0,r,s∈Q);②(a r)s=a rs(a>0,r,s∈Q);③(ab)r=a r b r(a>0,b>0,r∈Q).考点3 指数函数的图象与性质四、例题精析 【例题1】【题干】化简下列各式(其中各字母均为正数).121121332··a b a b ---⎛⎫ ⎪; (2)56a 13·b -2·⎝⎛⎭⎫-3a 12-b -1÷⎝⎛⎭⎫4a 23·b -312.【答案】(1)110(2)a 4a(3)a【解析】(1)原式=111133221566·a b a ba b--==a111326---·b115236+-=1a.(2)原式=-52a16-b-3÷⎝⎛⎭⎫4a23·b-312=-54a16-·b-3÷⎝⎛⎭⎫a13b32-=-54a12-·b32-.=-54·1ab3=-5ab4ab2.【例题2】【题干】函数y=a x-a(a>0,且a≠1)的图象可能是()【答案】 C【解析】当x=1时,y=a1-a=0,∴函数y=a x-a的图象过定点(1,0),结合图象可知选C.【例题3】【题干】设a>0且a≠1,函数y=a2x+2a x-1在[-1,1]上的最大值是14,求a的值.【解析】令t =a x (a >0且a ≠1),则原函数化为y =(t +1)2-2(t >0).①当0<a <1时,x ∈[-1,1],t =a x∈⎣⎢⎡⎦⎥⎤a ,1a , 此时f (t )在⎣⎢⎡⎦⎥⎤a ,1a 上为增函数. 所以f (t )max =f ⎝ ⎛⎭⎪⎫1a =⎝ ⎛⎭⎪⎫1a +12-2=14. 所以⎝ ⎛⎭⎪⎫1a +12=16,即a =-15或a =13. 又因为a >0,所以a =13.②当a >1时,x ∈[-1,1],t =a x ∈⎣⎢⎡⎦⎥⎤1a ,a , 此时f (t )在⎣⎢⎡⎦⎥⎤1a ,a 上是增函数.所以f (t )max =f (a )=(a +1)2-2=14, 解得a =3(a =-5舍去).综上得a =13或a =3.五、课堂运用【基础】1.化简-x3x的结果是()A.--x B.x C.-x D.-x-x3x=--x3x2=--x.解析:选A依题意知x<0,∴2.函数y =⎝ ⎛⎭⎪⎫13x 2 的值域是( ) A .(0,+∞) B .(0,1)C .(0,1]D .[1,+∞)解析:选C ∵x 2≥0,∴⎝ ⎛⎭⎪⎫13x 2≤1,即值域是(0,1].3.设函数f (x )定义在实数集上,它的图象关于直线x =1对称,且当x ≥1时,f (x )=3x -1,则有( )A .f ⎝ ⎛⎭⎪⎫13<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫23B .f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫13C .f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫13<f ⎝ ⎛⎭⎪⎫32D .f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫13解析:选B 由题设知,当x ≥1时,f (x )=3x -1单调递增,因其图象关于直线x =1对称,∴当x ≤1时,f (x )单调递减.∴f ⎝ ⎛⎭⎪⎫32=f ⎝ ⎛⎭⎪⎫2-32=f ⎝ ⎛⎭⎪⎫12.∴f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫12<f ⎝ ⎛⎭⎪⎫13,即f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫13.【巩固】4.已知函数f(x)=4+a x-1的图象恒过定点P,则点P的坐标是________.解析:令x-1=0,即x=1,则f(1)=5. ∴图象恒过定点P(1,5).答案:(1,5)5.对于函数f(x),如果存在函数g(x)=ax+b(a,b为常数),使得对于区间D上的一切实数x都有f(x)≤g(x)成立,则称函数g(x)为函数f(x)在区间D上的一个“覆盖函数”,设f(x)=2x,g(x)=2x,若函数g(x)为函数f(x)在区间[m,n]上的一个“覆盖函数”,则|m-n|的最大值为________.解析:因为函数f(x)=2x与g(x)=2x的图象相交于点A(1,2),B(2,4),由图可知,[m,n]⊆[1,2],故|m-n|max=2-1=1.答案:1【拔高】6.已知定义域为R的函数f(x)=-2x+b2x+1+a是奇函数.(1)求a,b的值;(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.解:(1)因为f(x)是R上的奇函数,所以f(0)=0,即-1+b2+a=0,解得b=1.从而有f(x)=-2x+1 2x+1+a.又由f(1)=-f(-1)知-2+14+a=--12+11+a,解得a=2.(2)由(1)知f(x)=-2x+12x+1+2=-12+12x+1,由上式易知f(x)在R上为减函数,又因为f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k).因为f(x)是R上的减函数,由上式推得t2-2t>-2t2+k.即对一切t∈R有3t2-2t-k>0,从而Δ=4+12k<0,解得k<-1 3.7.若函数y=lg(3-4x+x2)的定义域为M.当x∈M时,求f(x)=2x+2-3×4x的最值及相应的x的值.解:y =lg (3-4x +x 2),∴3-4x +x 2>0,解得x <1或x >3.∴M ={x |x <1,或x >3}.f (x )=2x +2-3×4x =4×2x -3×(2x )2.令2x =t ,∵x <1或x >3,∴t >8或0<t <2.∴y =4t -3t 2=-3⎝ ⎛⎭⎪⎫t -232+43(t >8或0<t <2). 由二次函数性质可知:当0<t <2时,f (t )∈⎝ ⎛⎦⎥⎤-4,43, 当t >8时,f (t )∈(-∞,-160),∴当2x =t =23,即x =log 223时,f (x )max =43.综上可知,当x =log 223时,f (x )取到最大值为43,无最小值.课程小结1.分数指数幂与根式的关系:分数指数幂与根式可以相互转化,通常利用分数指数幂的意义把根式的运算转化为幂的运算,从而简化计算过程.2.指数函数的单调性是由底数a的大小决定的,因此解题时通常对底数a按0<a<1和a>1进行分类讨论.。

2.1.1 指数与指数幂的运算(一)(一)教学目标1.知识与技能(1)理解n次方根与根式的概念;(2)正确运用根式运算性质化简、求值;(3)了解分类讨论思想在解题中的应用.2.过程与方法通过与初中所学的知识(平方根、立方根)进行类比,得出n次方根的概念,进而学习根式的性质.3.情感、态度与价值观(1)通过运算训练,养成学生严谨治学,一丝不苟的学习习惯;(2)培养学生认识、接受新事物的能力.(二)教学重点、难点1.教学重点:(1)根式概念的理解;(2)掌握并运用根式的运算性质.2.教学难点:根式概念的理解.(三)教学方法:本节概念性较强,为突破根式概念的理解这一难点,使学生易于接受,故可以从初中已经熟悉的平方根、立方根的概念入手,由特殊逐渐地过渡到一般的n次方根的概念,在得出根式概念后,要引导学生注意它与n次方根的关系,并强调说明根式是n次方根的一种表示形式,加强学生对概念的理解,并引导学生主动参与了教学活动.故本节课可以采用类比发现,学生合作交流,自主探索的教学方法.(四)教学过程:一、引入课题1.以折纸问题引入,激发学生的求知欲望和学习指数概念的积极性2.由实例(见教材P48—49)引入,了解指数的意义是什么,指数概念提出的背景,体会引入指数的必要性;3.初中根式的概念;如果一个数的平方等于a,那么这个数叫做a的平方根,如果一个数的立方等于a,那么这个数叫做a的立方根;二、新课教学(一)指数与指数幂的运算1.根式的概念x n ,那么x叫做a的n次方根(n th root),其中n>1,且n∈N*.一般地,如果a当n是奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数.此时,a的n次方根用符号n a表示.式子n a叫做根式(radical),这里n叫做根指数(radical exponent),a叫做被开方数(radicand).当n 是偶数时,正数的n 次方根有两个,这两个数互为相反数.此时,正数a 的正的n 次方根用符号na 表示,负的n 次方根用符号-n a 表示.正的n 次方根与负的n 次方根可以合并成±n a (a >0).由此可得:负数没有偶次方根;0的任何次方根都是0,记作00=n.思考:(课本P 50探究问题)nn a =a 一定成立吗?.(学生活动) 结论:当n 是奇数时,a a nn =当n 是偶数时,⎩⎨⎧<≥-==)0()0(||a a a a a a nn 三.例题讲解例1.(教材P 50例1). 略 补充例题(按情况讲解)例21,a =-a 求的取值范围.例3例4四.巩固练习: 练习 计算下列各式的值.(1)33)(a ;(2 (1n >,且n N *∈)(3)1n >,且n N *∈)五.归纳总结1.根式的概念:若n >1且*n N ∈,则n x a 是的次方根.x n 为奇数时, n 为偶数时,x =2.掌握两个公式:,n n 为奇数时(0)||(0)a a n a a a ≥⎧==⎨-<⎩为偶数时 六.课后作业: 七.板书设计:(略) 八.课后反思:2.1.2 指数与指数幂的运算(二)(一)教学目标1.知识与技能(1)理解分数指数幂的概念;(2)掌握分数指数幂和根式之间的互化;(3)掌握分数指数幂的运算性质;(4)培养学生观察分析、抽象等的能力.2.过程与方法通过与初中所学的知识进行类比,得出分数指数幂的概念,和指数幂的性质.3.情感、态度与价值观(1)培养学生观察分析,抽象的能力,渗透“转化”的数学思想;(2)通过运算训练,养成学生严谨治学,一丝不苟的学习习惯;(3)让学生体验数学的简洁美和统一美.(二)教学重点、难点1.教学重点:(1)分数指数幂的理解;(2)掌握并运用分数指数幂的运算性质;2.教学难点:分数指数幂概念的理解(三)教学方法发现教学法1.经历由利用根式的运算性质对根式的化简,注意发现并归纳其变形特点,进而由特殊情形归纳出一般规律.2.在学生掌握了有理指数幂的运算性质后,进一步推广到实数范围内.由此让学生体会发现规律,并由特殊推广到一般的研究方法.(四)教学过程:一.引入课题1.n次方根的定义记法nnnnaa ⎧⎪⎨±⎪⎩为奇数为偶数2.根式:n a3. 3.{,||,a n a n 为奇数为偶数巩固强化知识点,为本节课的教学奠定知识基础 二.新课讲授1.回顾正整数指数幂导出探究的问题 能否这样表示?指出当根式的被开方数能被根指数整除时,根式可以表示为分数指数幂的形式,能否将这个结论推广到正数的正分数指数幂的形式上去? 2.分数指数幂 正数的分数指数幂的意义规定:)1,,,0(*>∈>=n N n m a a an m nm)1,,,0(11*>∈>==-n N n m aa aanmnm nm0的正分数指数幂等于0,0的负分数指数幂没有意义指出:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂. 3.有理指数幂的运算性质(1)r a ·s r ra a +=),,0(Q s r a ∈>; (2)rs s ra a=)(),,0(Q s r a ∈>; (3)s r ra a ab =)(),0,0(Q r b a ∈>>.三.例题讲解引导学生解决本课开头实例问题例题.(教材P 51例2、例3、例4、例5) 补充例题 例1计算(1).)01.0(41225325.02120-⎪⎭⎫⎝⎛⋅+⎪⎭⎫ ⎝⎛--==412510)2()1(a a 34432552)()(aa a a ==412510aa ==)0()0(>>a a ()4315220aaa a ===>(1)5.1213241)91()6449()27()0001.0(---+-+; 例2.化简下列各式:(1)313315383327----÷÷a a a a a a ;(2)33323323134)21(248a ab a abb b a a ⨯-÷++-. 说明:让学生熟练掌握根式与分数指数幂的互化和有理指数幂的运算性质运用. 巩固练习:(教材P 54练习1-3) 4. 无理指数幂结合教材P 52实例利用逼近的思想理解无理指数幂的意义.指出:一般地,无理数指数幂),0(是无理数αα>a a是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.有理数指数幂推广到无理数指数幂,进而推广到整个实数范围,说明可以用指数的运算来解决生活中的实际问题.四.课堂小结1. 正数的正分数指数幂的意义2. 正数的负分数指数幂的意义3. 运算性质五.课后作业 六.板书设计(略) 七.课后反思:2.1.3 指数函数及其性质(一)(一)教学目标1.知识与技能了解指数函数模型的实际背景,理解指数函数的概念,掌握指数函数的图象. 2.过程与方法能借助计算器或计算机画出具体指数函数的图象,探索指数函数图象特征. 3.情感、态度与价值观在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型,激发学生学习数学的兴趣,努力培养学生的创新意识.(二)教学重点、难点1.教学重点:指数函数的概念和图象. 2.教学难点:指数函数的概念和图象. (三)教学方法采用观察、分析、归纳、抽象、概括,自主探究,合作交流的教学方法,通过各种教学媒体(如计算机或计算器),调动学生参与课堂教学的主动性和积极性. (四)教学过程 一.复习引入1. 在本章的开头,问题(1)中时间x 与GDP 值中的1.073(20)x y x x =∈≤与问题(2)中时间t 和C-14含量P 的对应关系]t 51301P=[()2,请问这两个函数有什么共同特征. 2. 这两个函数有什么共同特征157301][()]2t P =t57301把P=[()变成2,从而得出这两个关系式中的底数是一个正数,自变量为指数,即都可以用x y a =(a >0且a ≠1来表示).二.新课讲授 1.指数函数的定义 一般地,函数x y a =(a >0且a ≠1)叫做指数函数(exponential function),其中x 是自变量,函数的定义域为R .提问:在下列的关系式中,哪些不是指数函数,为什么?(1)22x y += (2)(2)x y =- (3)2x y =-(4)x y π= (5)2y x = (6)24y x = (7)x y x = (8)(1)x y a =- (a >1,且2a ≠)小结:根据指数函数的定义来判断说明:因为a >0,x 是任意一个实数时,xa 是一个确定的实数,所以函数的定义域为实数集R .000,0xx a a x a ⎧>⎪=⎨≤⎪⎩x当时,等于若当时,无意义若a <0,如1(2),,8x y x x =-=1先时,对于=等等,6在实数范围内的函数值不存在.若a =1,11,x y == 是一个常量,没有研究的意义,只有满足(0,1)x y a a a =>≠且的形式才能称为指数函数,5,,3,31x x x a y x y y +===+1xx为常数,象y=2-3,y=2等等,不符合(01)x y a a a =>≠且的形式,所以不是指数函数2.指数函数的性质我们在学习函数的单调性的时候,主要是根据函数的图象,即用数形结合的方法来研究. 先来研究a >1的情况 下面我们通过用计算机完成以下表格,并且用计算机画出函数2x y =的图象再研究,0<a <1的情况,用计算机完成以下表格并绘出函数1()2x y =的图象.从图中我们看出12()2x x y y ==与的图象有什么关系?通过图象看出12()2x x y y y ==与的图象关于轴对称,实质是2xy =上的x,y 点(-)x y x,y y 1与=()上点(-)关于轴对称.2讨论: 1.12()2x x y y ==与的图象关于y 轴对称,所以这两个函数是偶函数,对吗?2.画出115,3,(),()35x xx x y y y y ====的函数图象.问题:1:从画出的图象中,你能发现函数的图象与底数间有什么样的规律.x x.问题2:根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大(小)值、奇偶性. 问题3:指数函数x y a =(a >0且a ≠1),当底数越大时,函数图象间有什么样的关系.指数函数的图象和性质x y a =三.例题讲解例1 比较下列各题中两个数的大小:(1) 3 0.8 ,30.7(2) 0.75-0.1, 0.750.1四.课堂练习练习p58 1,2五.板书设计六.课后反思:2.1.2 指数函数及其性质(二) (一)教学目标 1.知识与技能: (1)理解指数函数的概念和意义,根据图象理解和掌握指数函数的性质.(2)体会具体到一般数学讨论方式及数形结合的思想;2.过程与方法:展示函数图象,让学生通过观察,进而研究指数函数的性质.3.情感、态度与价值观(1)让学生了解数学来自生活,数学又服务于生活的哲理.(2)培养学生观察问题,分析问题的能力.(二)教学重点、难点1.教学重点:指数函数的概念和性质及其应用.2.教学难点:指数函数性质的归纳,概括及其应用.(三)教学方法采用观察、分析、归纳、抽象、概括,自主探究,合作交流的教学方法,利用多媒体教学,使学生通过观察图象,总结出指数函数的性质,调动学生参与课堂教学的主动性和积极性.从而培养学生的观察能力,概括能力.(四)教学过程一.复习引入复习指数函数的概念和图象.1.指数函数的定义2.指数函数的图象问题:根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大(小)值、奇偶性.问题:指数函数x y a (a >0且a ≠1),当底数越大时,函数图象间有什么样的关系.二.新科讲授一.例题讲解题型一:单调区间的求法例1:求下列函数的单调区间:(1)223x x y a +-=; (2)10.21x y =- 题型二:与指数有关的定义域(值域)问题 例2 :(1)求下列函数的定义域、值域(1)y=22)21(++-x x ; (2)110.3x y -=; (3)513x y -=(2).求函数4225x x y =-⋅+,[0,2]x ∈的最大值和最小值.练习 求函数2233x x y -++=的定义域、值域并指出单调区间.题型三:与指数函数有关的图象问题1.如图指数函数①x y a =②x y b =③x y c =④x y d =的图象,则 ( ) (A )01a b c d <<<<<(B )01b a d c <<<<<(C )1a b c d <<<<(D )01a b d c <<<<<题型四:指数函数图象与方程和不等式例4:(2)求方程24x x +=的解的个数练习:补充例题 例题:已知f(x)=11+-x x a a (a>0,且a 1≠)(1)求f(x)的定义域和值域; (2)判断f(x)的奇偶性;(3)讨论f(x)的单调性;练习:已知21()21x x f x -=+. (1)讨论()f x 的奇偶性; (2)讨论()f x 的单调性. 二.课堂练习1.函数2651()()3x x f x -+=的单调递减区间为( ). A. (,)-∞+∞ B. [3,3]- C. (,3]-∞ D. [3,)+∞2.定义运算()() , .a a b a b b a b ≤⎧⎪*=⎨>⎪⎩ 则函数()12x f x =*的值域为 . 3:设a 是实数,2()()21x f x a x R =-∈+, (1)求a 的值,使函数()f x 为奇函数(2)试证明:对于任意,()a f x 在R 为增函数;三.课后作业四.板书设计五.课后反思。

指数与指数函数一、学习目标1、理解n资助方根、根式、分数指数幂概念,会对根式、分数指数幂进行互化;2、掌握分数指数幂的运算性质,熟练运用性质进行化简、求值;3、培养化归意识,思维的灵活性和严密性;4、掌握指数函数的根念;5、掌握指数函数的图像、性质;6、能利用指数函数的性质比较幂的大小;7、培养学生的应用意识。
二、例题分析第一阶梯[例1]求下列各式的值;分析:根式可化为分数指数幂形式,利用分数指数幂运算性质计算。
解:说明:既含有分数指数幂,又有根式,一般把根式统一化成分数指数幂的形式,便于计算,如果根式中根指数不同,也应化成分数指数幂的形式。
例2、指出下列函数中哪些是指数函数;(1)y=4x; (2)y=x4; (3)y=-4x; (4)y=(-4)x; (5)y=πx;(7)y=xx;分析:根据指数函数定义进行判断。
解:(1)、(5)为指数函数;(2)不是指数函数;(3)是-1与指数函数4x的乘积;(4)中底数-4<0,∴不是指数函数;(6)中指数不是自变量x,而是x的函数x2;(7)中底数x不是常数。
它们都不符合指数函数的定义。
说明:指数函数严格限定在y=ax(a>0且a≠1)这一结构,(2)(3)(4)(6)(7)均不是指数函数,不具备指数函数的基本性质。
第二阶梯例3、A、1B、2a-1C、1或2a-1D、0思路分析:根据根式的意义直接进行判断.解:(2)取a=0,b=1,A不成立;取a=0,b=-1,C不成立;取a=-1,b=-1,D不成立;因为a2+b2≥0,所以B正确,故选B.答案:(1)C (2)B例4、函数f(x)=x2-bx+c满足f(1+x)=f(1-x),且f(0)=3,则f(bx)与f(cx)的大小关系是_______。
思路分析:利用二次函数、指数函数的单调性,结合函数的有关知识进行解答。
解答:∵f(1+x)=f(1-x),∴f(x)的对称轴为x=1,由此得b=2,又∵f(0)=3,∴c=3.∴f(x)=x2-2x+3在(-∞,1)内递减,在(1,+∞)内递增。

指数与指数函数教案教案标题:指数与指数函数教案教案目标:1. 理解指数的概念和基本性质;2. 掌握指数运算的基本法则;3. 理解指数函数的定义和特点;4. 能够应用指数函数解决实际问题。
教学重点:1. 指数的定义和基本性质;2. 指数运算的基本法则;3. 指数函数的定义和特点。
教学难点:1. 指数函数的应用问题解决。
教学准备:1. 教材:包含有关指数和指数函数的相关知识的教材;2. 教具:计算器、白板、彩色粉笔等。
教学过程:一、导入(5分钟)1. 引入指数的概念,通过实例解释指数的含义和作用;2. 提问学生对指数的了解程度,激发学生的学习兴趣。
二、讲解指数的定义和基本性质(15分钟)1. 讲解指数的定义,包括底数、指数和幂的概念;2. 介绍指数的基本性质,如指数为0时的计算规则、指数为正数时的计算规则等;3. 通过例题演示指数运算的基本法则。
三、指数运算练习(15分钟)1. 给学生分发练习题,要求他们完成指数运算的计算和简化;2. 引导学生互相讨论解题思路和方法;3. 随堂检查学生的练习成果,及时纠正错误。
四、讲解指数函数的定义和特点(15分钟)1. 介绍指数函数的定义,包括指数为变量的函数形式;2. 解释指数函数的特点,如增长率、图像特征等;3. 通过图像展示指数函数的变化规律。
五、指数函数应用实例分析(15分钟)1. 给学生提供一些实际问题,要求他们运用指数函数解决;2. 引导学生分析问题,建立数学模型;3. 鼓励学生互相交流和分享解题思路。
六、小结与拓展(10分钟)1. 总结指数与指数函数的重点内容和学习要点;2. 提出一些拓展问题,激发学生进一步思考;3. 鼓励学生自主学习相关知识,拓宽数学视野。
教学反馈:1. 教师及时纠正学生在课堂上的错误,解答学生提出的问题;2. 教师评价学生的参与度和学习成果;3. 学生填写教学反馈表,反馈课堂教学的效果和自身的学习感受。
教学延伸:1. 布置相关练习作业,巩固学生的学习成果;2. 鼓励学生使用计算器和其他工具进行指数函数的实际计算;3. 推荐相关参考书籍和网站,供学生进一步学习。

指数与指数函数教学目标:掌握指数运算(高考要求A )及指数函数的有关概念(高考要求B ). 教学重难点:熟悉指数运算,掌握指数函数图像性质及其应用。
教学过程: 一.知识要点: 1.指数运算(1) 根式的定义:若一个数的n 次方等于),1(*∈>N n n a 且,则这个数称a 的n 次方根。
即若a x n =,则x 称a 的n 次方根()1*∈>N n n 且, ① 当n 为奇数时,n a 的次方根记作n a ;②当n 为偶数时,负数a 没有n 次方根,而正数a 有两个n 次方根且互为相反数,记作)0(>±a a n 。
(2)根式性质:①a a n n =)(;②当n 为奇数时,a a n n =;③当n(0)||(0)a a a a a ≥⎧==⎨-<⎩。
(3)幂运算法则:①∈⋅⋅⋅=n a a a a n ( N *) ②)0(10≠=a a ;n 个 ③∈=-p aap p(1Q ,4)m a a a n m n m,0(>=、∈n N *且)1>n 。
(4)幂运算性质: ①r a a a a sr s r ,0(>=⋅+、∈s Q );②r a a a s r s r ,0()(>=⋅、∈s Q ); ③∈>>⋅=⋅r b a b a b a r r r ,0,0()( Q )。
(注)上述性质对r 、∈s R 均适用。
2.指数函数:(1) 指数函数定义:函数)1,0(≠>=a a a y x 且称指数函数,函数的定义域为R ;函数的值域为),0(+∞; (2)函数图像及性质:①指数函数的图象都经过点(0,1),且图象都在第一、二象限;②当10<<a 时函数为减函数,当1>a 时函数为增函数。
③指数函数都以x 轴为渐近线(当10<<a 时,图象向左无限接近x 轴,当1>a 时,图象向右无限接近x 轴);④对于相同的)1,0(≠>a a a 且,函数x x a y a y -==与的图象关于y 轴对称。


2.1.2 指数函数及其性质(1)三维目标一、知识与技能1.掌握指数函数的概念、图象和性质..能借助计算机或计算器画指数函数的图象. 3.能由指数函数图象探索并理解指数函数的性质. 二、过程与方法1.在学习的过程中体会研究具体函数及其性质的过程和方法,如具体到一般的过程,数形结合的方法等.2.通过探讨指数函数的底数a >0,且a ≠1的理由,明确数学概念的严谨性和科学性,做一个具备严谨科学态度的人.三、情感态度与价值观1.通过实例引入指数函数,激发学生学习指数函数的兴趣,体会指数函数是一类重要的函数模型,并且有广泛的用途,逐步培养学生的应用意识.2.在教学过程中,通过现代信息技术的合理应用,让学生体会到现代信息技术是认识世界的有效手段. 教学重点指数函数的概念和性质. 教学难点用数形结合的方法从具体到一般地探索、概括指数函数的性质. 教具准备多媒体、学案. 教学过程(一)新课导学探究一:指数函数的概念问题1:细胞分裂时,第一次由1个分裂成2个(即 12),第2次由2个分裂成4个(即 ),第3次由4个分裂成8个(即 ),如此下去,如果第x 次分裂得到 个细胞,那么细胞个数y 与次数x 的关系式是问题2:《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭。
”请你写出截取x 次后,木棰剩余量y 关于x 的关系式是【讨论】:(1)这两个关系式是否构成函数?我们发现:在两个关系式中,每给一个自变量都有唯一的一个函数值和它对应,因此关系式2x y= 和 1()2xy = 都是函数关系式。
(2)这是我们学过的哪个函数?如果不是,你能否根据该函数的特征给它起个恰当的名字?我们发现: 函数2x y= 和 1()2xy =在在形式上是是相同的,解析式的右边都是指数式,且自变量都在指数位置上。
底数是常数,指数是自变量。
结论:函数2x y= 和 1()2x y =都是函数y =a x 的具体形式.函数y =a x是一类重要的函数模型,并且有广泛的用途,它可以解决好多生活中的实际问题,这就是我们下面所要研究的一类重要函数模型——指数函数. (引入新课,书写课题)(二)概念讲解指数函数的概念:一般地,函数y =a x (a >0,a ≠1)叫做指数函数,其中x 是自变量,函数的定义域是R . 思考:1、指数函数解析式的结构特征: ①xa 前面的系数为:1 ②a 的取值范围:a >0,a ≠1③指数只含x2:为什么规定10≠>a a 且呢?否则会出现什么情况呢?①当0=a ,ⅰ若0>x ,则00=xⅱ若0≤x ,则x0无意义,如:21-=x ,则010102121===-y 无意义。

指数函数教案设计一、教学目标知识与技能:1. 理解指数函数的定义和性质。
2. 掌握指数函数的图象和应用。
3. 学会解决与指数函数相关的问题。
过程与方法:1. 通过观察、分析和归纳,探索指数函数的性质。
2. 利用指数函数模型解决实际问题。
情感态度价值观:1. 培养学生的数学思维能力。
2. 激发学生对数学的兴趣和好奇心。
二、教学内容第一节:指数函数的定义与性质1. 引入指数函数的概念。
2. 分析指数函数的性质:单调性、奇偶性、周期性。
第二节:指数函数的图象1. 绘制常见指数函数的图象。
2. 分析指数函数图象的特点。
第三节:指数函数的应用1. 应用指数函数解决实际问题。
2. 利用指数函数模型进行预测和计算。
三、教学方法采用问题驱动法、案例教学法和讨论法。
通过提出问题、分析问题、解决问题的过程,引导学生主动探索指数函数的性质和应用。
利用实际案例,让学生体验数学与生活的紧密联系。
通过小组讨论,培养学生的合作能力和口头表达能力。
四、教学资源1. 教案、PPT课件。
2. 指数函数相关案例资料。
3. 计算器、白板等教学工具。
五、教学评价1. 课堂参与度:观察学生在课堂上的发言和提问情况,评估学生的参与程度。
2. 作业完成情况:检查学生作业的完成质量和速度。
3. 小组讨论:评估学生在讨论中的表现,包括观点阐述、合作能力和解决问题的能力。
4. 课后反馈:收集学生对课堂内容和教学方法的反馈,以便进行教学改进。
六、教学安排第一节:指数函数的定义与性质(45分钟)1. 引入指数函数的概念(10分钟)2. 分析指数函数的性质:单调性、奇偶性、周期性(25分钟)3. 练习与讨论(10分钟)第二节:指数函数的图象(45分钟)1. 绘制常见指数函数的图象(20分钟)2. 分析指数函数图象的特点(20分钟)3. 练习与讨论(5分钟)第三节:指数函数的应用(45分钟)1. 应用指数函数解决实际问题(20分钟)2. 利用指数函数模型进行预测和计算(20分钟)3. 练习与讨论(5分钟)七、教学反思在授课过程中,注意观察学生的反应,根据学生的实际情况调整教学节奏和内容。

指数函数教案(精选多篇)第一篇:指数函数教案.doc一.思考题1.来回答其变化的过程和答案2.过ppt来讲解思考题二、问题1.接说出指数函数2.学来思考问题23.出指数函数的概念三.例题1.下题目,叫学生思考几秒钟,请学生来回答。
2.学生的回答进行分析四.思考1.第一个思考,引导学生说出图像的做法,2.学生来画出4个图像3.图像进行补充4.函数的三要素来分析图像的性质5.图像上的到恒过的点及单调性6.行底数互为倒数的函数图像的比较、得到对称的性质(换算)7.行底数不同大小的比较,说明其大小的变化五.例题先思考,再请同学来回答,再进行点评六、总结七、布置作业第二篇:《指数函数概念》教案《指数函数概念》教案(一)情景设置,形成概念1、引例1:折纸问题:让学生动手折纸观察:①对折的次数x与所得的层数y之间的关系,得出结论y=2x②对折的次数x与折后面积y之间的关系(记折前纸张面积为1),得出结论y=(1/2)x引例2:《庄子。
天下篇》中写到:“一尺之棰,日取其半,万世不竭”。
请写出取x次后,木棰的剩留量与y与x的函数关系式。
2、形成概念:形如y=ax(a>0且a≠1)的函数称为指数函数,定义域为x∈r。
提出问题:为什么要限制a>0且a≠1?这一点让学生分析,互相补充。
分a﹤=0,a=1讨论。
1)a<0时,y=(-3)x对于x=1/2,1/4,??(-3)x无意义。
2)a=0时,x>0时,ax=0;x≤0时无意义。
3)a=1时,a= 1=1是常量,没有研究的必要。
(二)发现问题、深化概念问题:判断下列函数是否为指数函数。
1)y=-3x2)y=31/x3) y=31+x4) y=(-3)x5) y=3-x=(1/3) x1、1)ax的前面系数为1; 2)自变量x在指数位置; 3)a>0且a≠1。
2、问题中4)y=(-3)x的判定,引出上面讨论的问题:即指数函数的概念中为什么要规定a>0且a≠1。

指数与指数函数教学目标:掌握指数运算(高考要求A )及指数函数的有关概念(高考要求B ). 教学重难点:熟悉指数运算,掌握指数函数图像性质及其应用。
教学过程: 一.知识要点: 1.指数运算(1) 根式的定义:若一个数的n 次方等于),1(*∈>N n n a 且,则这个数称a 的n 次方根。
即若a x n =,则x 称a 的n 次方根()1*∈>N n n 且, ① 当n 为奇数时,n a 的次方根记作n a ;②当n 为偶数时,负数a 没有n 次方根,而正数a 有两个n 次方根且互为相反数,记作)0(>±a a n 。
(2)根式性质:①a a n n =)(;②当n 为奇数时,a a n n =;③当n(0)||(0)a a a a a ≥⎧==⎨-<⎩。
(3)幂运算法则:①∈⋅⋅⋅=n a a a a n ( N *) ②)0(10≠=a a ;n 个 ③∈=-p aap p(1Q ,4)m a a a n m n m,0(>=、∈n N *且)1>n 。
(4)幂运算性质: ①r a a a a sr s r ,0(>=⋅+、∈s Q );②r a a a s r s r ,0()(>=⋅、∈s Q ); ③∈>>⋅=⋅r b a b a b a r r r ,0,0()( Q )。
(注)上述性质对r 、∈s R 均适用。
2.指数函数:(1) 指数函数定义:函数)1,0(≠>=a a a y x 且称指数函数,函数的定义域为R ;函数的值域为),0(+∞; (2)函数图像及性质:①指数函数的图象都经过点(0,1),且图象都在第一、二象限;②当10<<a 时函数为减函数,当1>a 时函数为增函数。
③指数函数都以x 轴为渐近线(当10<<a 时,图象向左无限接近x 轴,当1>a 时,图象向右无限接近x 轴);④对于相同的)1,0(≠>a a a 且,函数x x a y a y -==与的图象关于y 轴对称。
指数函数Module 1HobbiesUnit 1 What’s your hobby?一、兴趣爱好的词组:1.play computer games玩电脑游戏2.play music玩音乐3. collect stamps 集邮4.keep pets养宠物5.make model ships做轮船模型6. read books读书7.take photos 照相8.make cakes做蛋糕9. plant trees种树10. grow flowers种花11.listen to music听音乐12. singing,唱歌13.dancing跳舞14.drawing画画15.play the piano弹钢琴16.play chess下棋17. play basketball 打篮球…二、课文短语:1.make model ships 做轮船模型2.love making 喜欢制作3.more than 20 ships 超过20艘轮船4.collect stamps 集邮5.keep pets 养宠物6. Three birds 三只鸟7.play music 玩音乐8. every day 每天9.read books 读书10. every night 每天晚上11.play computer games 玩电脑游戏12.about 50 games 大约50个游戏13.take photos 照相14.during my holiday 在我的假期里三、句型:1. What’s your hobby?2. Do you like…?Yes, I do. / No, I don’t.3. I love/like…I like/love dancing .4. I enjoy …I enjoy listening to music.5. My (favourite) hobby is …6. …is my (favourite) hobby.7. Is your hobby keeping pets?Yes, it’s. / No, it isn’t.Unit 2 His hobby is drawing一、课文短语:1.a great painter 一个伟大的画家2.draw cartoons 画漫画3.coloured pencils 彩色的铅笔4.his pet dog 他的宠物狗5.in the sky 在天空中6.birthday cards 生日卡片7.for his friends 给他的朋友们8.on their birthday 在他们的生日9.interesting people 有趣的人物10.beautiful places 美丽的风景11.in every room 在每一个房间12.in her house 在她的房子里13.二、句型:14.1. What’s Mike’s hobby?His hobby is …15.2. When does Mike usually draw? Mike通常在什么时候画画?He usually draws ….16.3. What does Mike give his friends for their birthday?17.4. What present does Amy give to T om?18.5. What does she want to do when she grows up?She wants to be a writer.19.三、重点精析:20.1. grow up 成长,长大want to do…想要做…21.如:When Lucy grows up she wants to be an English teacher.22.当露丝长大后,她想成为一名英语教师。
指数与指数函数一、教学目标1.理解分数指数的概念,掌握有理指数幂的运算性质. 2.掌握指数函数的概念,图象和性质.二、重点、难点讲解1. 指数 (1)根式若x n=a(n>1,且*∈N n ),则x 叫做a 的n 次方根.当n 为奇数时,a 的n 次方根是n a .当n 为偶数时,若a>0,a 的n 次方根有2个,这两个方根互为相反数,即n a ±,其中正的一个n a 叫做a 的n 次算术根;若a=0,0的n 次方根只有一个,是0;若a<0,a 的n 次方根不存在(在实数范围内).当n 为奇数时,a a n n =.当n 为偶数时,=nna ⎩⎨⎧-a a(2)指数概念的推广①零指数.若运用指数运算法则,0a aa a nn nn==÷-,又有1=÷n n a a ,因此规定)0(10≠=a a .②负整数指数.若运用指数运算法则,n nnna aa a a --==÷=÷001,又有n n aa 11=÷,因此规定),0(1*-∈>=N n a aa n n . ③正分数指数.若运用指数运算法则,m n nm nnm a aa ==⋅)(,因此规定).1,,,0(>∈>=*n N n m a a an m nm 且④负分数指数,若运用指数运算法则,nm nm nm nm aaaa a--==÷=÷001,又有nm nm aa11=÷,因此规定)1,,,0(11>∈>==*-n N n m a a aanmnm nm 且且.⑤无理数指数,若a>0 ,p 是无理数,则a p也表示一个实数(因知识的原因,教材中对具体的规定已省略)(3)指数运算法则若a>0,b>0,Q s r ∈,,则有下列指数运算法则: ①sr sraa a +=⋅;(a ≥0), (a<0).xy 图11-11y=2y=10y=x xx 1②rss r a a =)(; ③rr r b a ab =)(.实际上上述法则当r,s 为无理数时也成立. 2.指数函数(1)形如y=a x)1,0(≠>a a 的函数叫做指数函数,因此xx y y π==,)31(都是指数函数,而x x y y 4,32-=⋅=均不能称为指数函数.(2)在y=a x中,当0≤a 时a x可能无意义,当a>0时x 可以取任何实数,当a=1时,)(1R x a x∈=,无研究价值,且这时11==xy 不存在反函数,因此规定y=a x中.1,0≠>a a 且(3)指数函数的图象和性质x a y =0 < a < 1 a > 1图 象性 质定义域 R值域(0 , +∞)定点过定点(0,1),即x = 0时,y = 1(1)a > 1,当x > 0时,y > 1;当x < 0时,0 < y < 1。
3..有理数指数幂 (1)幂的有关概念①正整数指数幂:)(a n a a a a a n 个⋅⋅⋅⋅⋅⋅⋅= (n ∈N *); ②零指数幂:a 0=1(a ≠0);③负整数指数幂:a -p=1ap (a ≠0,p ∈N *);④正分数指数幂:nm a =n m a (a >0,m 、n ∈ N *,且n >1); ⑤负分数指数幂:nmnm nm a aa11==-(a >0,m 、n ∈N *且n >1).⑥0的正分数指数幂等于0,0的负分数指数幂没有意义. (2)有理数指数幂的性质①n m n m a a a +=⋅ ②()n m nm a a ⋅= ()m m m b a ab ⋅= ④n m n m a a a -=÷例1.计算:2.化简(式中各字母均为正数):二:指数函数的图象与性质 1.定义:函数)1,0(≠>=a a ay x叫做指数函数,其中x 是自变量,函数的定义域为R.例1:判断下列函数是否是指数函数(1)5x y = (2)x y )5(-= (3)xy 52⋅=(4) 25+=xy (5)25+=x y (6)x y 25=答案:只有(6)是点评:按定义检验,注意(1)自变量的位置(2) a 的范围例2:求下列函数的定义域: (1)442x y -= (2)||2()3x y =2.性质:y =a xa >1 0<a <1图象定义域 R 值域 (0,+∞) 性质过定点(0,1)x <0时,0<y <1x <0时,y >1.在(-∞,+∞)上是增函数当x >0时,0<y <1; 当x >0时,y >1; 在(-∞,+∞)上是减函数例3:比较下列各题中两个值的大小:例4.(1)下图是指数函数①x y a = ②x y b = ③x y c = ④x y d =的图象,判断,,,a b c d1.33.09.07.13和)(35.27.17.11和)(2.01.08.08.02--和)(x y b =x y c =<1和a >1进行分类讨论.(2)换元时注意换元后“新元”的范围. 三个关键点画指数函数y =a x (a >0,且a ≠1)的图象,应抓住三个关键点:(1,a ),(0,1),⎪⎭⎫⎝⎛-a 11,课堂双基自测1.(2011·山东):若点(a,9)在函数y =3x的图象上,则tana π6的值为( ).A .0 B.33 C .1 D. 32.(2012·湖南) 函数f (x )=2|x -1|的图象是( ).3.若函数f (x )=12x +1,则该函数在(-∞,+∞)上是( ).A .单调递减无最小值B .单调递减有最小值C .单调递增无最大值D .单调递增有最大值4.(2012·天津) 已知 32121=+-a a ,则a +a -1=______;a 2+a -2=________. 作业:一、选择题1.下列函数一定是指数函数的是( )A .y =5x +1 ;B .y =x 4C .y =3-xD .y =2·3x2.函数131-⎪⎭⎫⎝⎛=x y 的值域是( )A .(-∞,0) ;B .(0,1];C .[1,+∞) ;D .(-∞,1]3.已知a =30.2,b =53,c =3-0.2,则a ,b ,c 三者的大小关系是( )A .a >b >c ;B .b >a >c ;C .c >a >b ;D .b >c >a。
指数与指数函数考纲要求:指数的概念及运算(B);指数函数的图像与性质(B) 知识梳理:1、指数的相关概念及运算;2、指数函数的定义: ;3、指数函数的图像与性质:基础训练:1、化简:3421413223)(a bb a ab b a ⋅= .)0,0(>>b a2、已知xx x f -+=22)(,若3)(=a f ,则=)2(a f . 3、0>∀x ,函数xa x f )1()(2-=的值总大于1,则实数a 的范围是 .4、函数m x f x -=--12)(的图象与x 轴有公共点时,实数m 的范围是 .例题选讲:例1、求下列函数的定义域、值域、增区间:⑴114.0-=x y ; ⑵153-=x y ; ⑶12+=xy . 定义域: 定义域: 定义域: 值 域: 值 域: 值 域: 增区间: 增区间: 增区间: 例2、已知函数)10(12)(2≠>-+=a a a a x f xx且在]1,1[-上的最大值为14,求实数a 的值.例3、画函数13-=x y 的图象,并用图象回答:k 为何值时,方程kx =-13无解?恰有一解?有两解?例4、已知函数[]11()()2()3,1,193x x f x a x =-+∈-)(R a ∈. ⑴求()()f x h a 的最小值;⑵是否存在实数m ,同时满足条件:①3m n >>;②当()h a 的定义域为[,]n m 时值域为22[,]n m ;若存在,求出,m n 的值;若不存在,说明理由.巩固练习:1、已知,9,91==b a 则315383327a a a a ⋅÷--的值为若⎩⎨⎧>≤=)0(ln )0()(x x x e x g x ,则=))21((g g .2、已知14)(-+=x ax f 的图象恒过定点P ,则点P 的坐标为 .3、已知函数121)(+-=x a x f 为奇函数,则=a .4、t x f x +=+13)(的图象不经过第二象限,则t 的取值范围为 .5、函数⎩⎨⎧≥<-+-=)0()0(33)(x a x a x x f x在R 上递减,则a 的范围是 .6、已知定义域为R 的函数a b x f x x ++-=+122)(是奇函数. ⑴求b a ,的值; ⑵判断并证明函数)(x f 的单调性;知 识 技 能 方 法⑶若对R t ∈∀,不等式0)2()2(22<-+-k t f t t f 恒成立,求k 的范围.。
指数与指数函数一、根式 1.根式的概念2.两个重要公式(1)n a n=⎩⎨⎧a , n 为奇数,|a |=⎩⎪⎨⎪⎧a (a ≥0),-a (a <0), n 为偶数;(2)(n a )n =a (注意a 必须使na 有意义). 二、有理数指数幂1.幂的有关概念(1)正分数指数幂:a m n =na m (a >0,m ,n ∈N *,且n >1);(2)负分数指数幂:a -m n =1a m n =1na m (a >0,m ,n ∈N *,且n >1);(3)0的正分数指数幂等于0,0的负分数指数幂没有意义. 2.有理数指数幂的性质 (1)a r a s=a r +s (a >0,r ,s ∈Q);(2)(a r )s =a rs (a >0,r ,s ∈Q); (3)(ab )r =a r b r (a >0,b >0,r ∈Q). 三、指数函数的图象和性质[基础自测]1.[(-2)6]12-(-1)0的结果为( )A .-9B .7C .-10D .9解析:选B 原式=(26)12-1=7.2.函数f (x )=1-2x 的定义域是( ) A .(-∞,0] B .[0,+∞) C .(-∞,0)D .(-∞,+∞)解析:选A ∵1-2x ≥0,∴2x ≤1,∴x ≤0. 3.已知函数f (x )=4+a x -1的图象恒过定点P ,则点P 的坐标是( ) A .(1,5) B .(1,4) C .(0,4)D .(4,0)解析:选A 当x =1时,f (x )=5.4.若函数y =(a 2-3a +3)·a x 是指数函数,则实数a 的值为________. 解析:∵a 2-3a +3=1,∴a =2或a =1(舍). 答案:25.若函数y =(a 2-1)x 在(-∞,+∞)上为减函数,则实数a 的取值范围是________. 解析:由题意知0<a 2-1<1,即1<a 2<2, 得-2<a <-1或1<a < 2. 答案:(-2,-1)∪(1,2)[例1] 化简下列各式(其中各字母均为正数). (1)(a 23·b -1)-12·a -12·b 136a ·b 5;(2)⎝⎛⎭⎫2790.5+0.1-2+⎝⎛⎭⎫21027-23-3π0+3748. [自主解答] (1)原式=a -13b 12·a -12b 13a 16b 56=a -13-12-16·b 12+13-56=1a.(2)原式=⎝⎛⎭⎫25912+10.12+⎝⎛⎭⎫6427-23-3+3748=53+100+916-3+3748=100. 总结:指数式的化简求值问题,要注意与其他代数式的化简规则相结合,遇到同底数幂相乘或相除,可依据同底数幂的运算规则进行,一般情况下,宜化负指数为正指数,化根式为分数指数幂.对于化简结果,形式力求统一.变式练习1.计算:(1)(0.027)-13-⎝⎛⎭⎫-17-2+⎝⎛⎭⎫27912-(2-1)0; (2)⎝⎛⎭⎫14-12·(4ab -1)30.1-2(a 3b -3)12.解:(1)原式=⎝⎛⎭⎫271 000-13-(-1)-2⎝⎛⎭⎫17-2+⎝⎛⎭⎫25912-1 =103-49+53-1=-45. (2)原式=412·432100·a 32·a -32·b 32·b -32=425a 0·b 0=425.[例2] 函数y =a x -a (a >0,且a ≠1)的图象可能是( )[自主解答] 法一:令y =a x -a =0,得x =1,即函数图象必过定点(1,0),符合条件的只有选项C.法二:当a >1时,y =a x -a 是由y =a x 向下平移a 个单位,且过(1,0),排除选项A 、B ; 当0<a <1时,y =a x -a 是由y =a x 向下平移a 个单位,因为0<a <1,故排除选项D. [答案] C总结:1.与指数函数有关的函数的图象的研究,往往利用相应指数函数的图象,通过平移、对称变换得到其图象.2.一些指数方程、不等式问题的求解,往往利用相应的指数型函数图象数形结合求解.变式练习2.(1)在同一坐标系中,函数y =2x 与y =⎝⎛⎭⎫12x 的图象之间的关系是( ) A .关于y 轴对称 B .关于x 轴对称 C .关于原点对称D .关于直线y =x 对称(2)方程2x =2-x 的解的个数是________.解析:(1)∵y =⎝⎛⎭⎫12x =2-x ,∴它与函数y =2x 的图象关于y 轴对称. (2)方程的解可看作函数y =2x 和y =2-x 的图象交点的横坐标,分别作出这两个函数图象(如图).由图象得只有一个交点,因此该方程只有一个解. 答案:(1)A (2)1[例3] 已知函数f (x )=⎝⎛⎭⎫23|x |-a.则函数f (x )的单调递增区间为________,单调递减区间为________.[自主解答] 令t =|x |-a ,则f (x )=⎝⎛⎭⎫23t ,不论a 取何值,t 在(-∞,0]上单调递减,在[0,+∞)上单调递增, 又y =⎝⎛⎭⎫23t 是单调递减的,因此f (x )的单调递增区间是(-∞,0], 单调递减区间是[0,+∞). [答案] (-∞,0] [0,+∞)在本例条件下,若f (x )的最大值等于94,则a =______.解析:由于f (x )的最大值是94,且94=⎝⎛⎭⎫23-2,所以g (x )=|x |-a 应该有最小值-2, 从而a =2. 答案:2总结:求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归纳为内层函数相关的问题加以解决.变式练习1.(1)已知a =20.2,b =0.40.2,c =0.40.6,则( ) A .a >b >c B .a >c >b C .c >a >bD .b >c >a(2)已知函数f (x )=e |x -a |(a 为常数).若f (x )在区间[1,+∞)上是增函数,则a 的取值范围是________.解析:(1)由0.2<0.6,0.4<1,并结合指数函数的图象可知0.40.2>0.40.6,即b >c ;因为a =20.2>1,b =0.40.2<1,所以a >b .综上,a >b >c .(2)结合函数图象求解.因为y =e u 是R 上的增函数,所以f (x )在[1,+∞)上单调递增,只需u =|x -a |在[1,+∞)上单调递增,由函数图象可知a ≤1.答案:(1)A (2)(-∞,1]课后练习A 组1.下列函数中值域为正实数集的是( ) A .y =-5x B .y =⎝⎛⎭⎫131-xC .y =⎝⎛⎭⎫12x -1D .y =1-2x解析:选B ∵1-x ∈R ,y =⎝⎛⎭⎫13x的值域是正实数集, ∴y =⎝⎛⎭⎫131-x 的值域是正实数集.2.已知f (x )=2x +2-x ,若f (a )=3,则f (2a )等于( )A .5B .7C .9D .11解析:选B 由f (a )=3得2a +2-a =3, 两边平方得22a +2-2a+2=9,即22a +2-2a=7,故f (2a )=7.3.函数f (x )=2|x -1|的图象是( )解析:选B ∵f (x )=⎩⎪⎨⎪⎧2x -1,x ≥1,⎝⎛⎭⎫12x -1,x <1,∴根据分段函数即可画出函数图象.4.已知f (x )=3x -b (2≤x ≤4,b 为常数)的图象经过点(2,1),则f (x )的值域( )A .[9,81]B .[3,9]C .[1,9]D .[1,+∞)解析:选C 由f (x )过定点(2,1)可知b =2,因f (x )=3x-2在[2,4]上是增函数,可知C 正确.5.设函数f (x )=a-|x |(a >0,且a ≠1),f (2)=4,则( ) A .f (-2)>f (-1) B .f (-1)>f (-2) C .f (1)>f (2)D .f (-2)>f (2)解析:选A ∵f (2)=4,∴a-|2|=4,∴a =12,∴f (x )=⎝⎛⎭⎫12-|x |=2|x |,∴f (x )是偶函数,当x ≥0时,f (x )=2x是增函数,∴x <0时,f (x )是减函数,∴f (-2)>f (-1).6.若(2m +1)12>(m 2+m -1)12,则实数m 的取值范围是( )A.⎝ ⎛⎦⎥⎤-∞,5-12 B.⎣⎢⎡⎭⎪⎫5-12,+∞C .(-1,2)D.⎣⎢⎡⎭⎪⎫5-12,2解析:选D 因为函数y =x 12的定义域为[0,+∞),且在定义域内为增函数,所以不等式等价于⎩⎪⎨⎪⎧2m +1≥0,m 2+m -1≥0,2m +1>m 2+m -1,解2m +1≥0,得m ≥-12;解m 2+m -1≥0,得m ≤-5-12或m ≥5-12;解2m +1>m 2+m -1,即m 2-m -2<0,得-1<m <2. 综上所述,m 的取值范围是5-12≤m <2. 7.⎝⎛⎭⎫32-13×⎝⎛⎭⎫-760+814×42- ⎝⎛⎭⎫-2323=________.解析:原式=⎝⎛⎭⎫2313×1+234×214-⎝⎛⎭⎫2313=2. 答案:28.已知正数a 满足a 2-2a -3=0,函数f (x )=a x ,若实数m 、n 满足f (m )>f (n ),则m 、n 的大小关系为________.解析:∵a 2-2a -3=0,∴a =3或a =-1(舍). 函数f (x )=a x 在R 上递增,由f (m )>f (n ),得m >n . 答案:m >n9.若函数f (x )=a |2x -4|(a >0,a ≠1)且f (1)=9.则f (x )的单调递减区间是________.解析:由f (1)=9得a 2=9,∴a =3.因此f (x )=3|2x-4|,又∵g (x )=|2x -4|的递减区间为(-∞,2],∴f (x )的单调递减区间是(-∞,2]. 答案:(-∞,2]10.求下列函数的定义域和值域. (1)y =⎝⎛⎭⎫122x -x 2;(2)y = 32x -1-19.解:(1)显然定义域为R.∵2x -x 2=-(x -1)2+1≤1, 且y =⎝⎛⎭⎫12x为减函数. ∴⎝⎛⎭⎫122x -x 2≥⎝⎛⎭⎫121=12.故函数y =⎝⎛⎭⎫122x -x 2的值域为⎣⎡⎭⎫12,+∞. (2)由32x -1-19≥0,得32x -1≥19=3-2,∵y =3x 为增函数,∴2x -1≥-2, 即x ≥-12,此函数的定义域为⎣⎡⎭⎫-12,+∞, 由上可知32x -1-19≥0,∴y ≥0.即函数的值域为[0,+∞).11.函数f (x )=a x (a >0,且a ≠1)在区间[1,2]上的最大值比最小值大a2,求a 的值.解:当a >1时,f (x )=a x 为增函数,在x ∈[1,2]上,f (x )最大=f (2)=a 2,f (x )最小=f (1)=a . ∴a 2-a =a2.即a (2a -3)=0.∴a =0(舍)或a =32>1.∴a =32.当0<a <1时,f (x )=a x 为减函数,在x ∈[1,2]上,f (x )最大=f (1)=a ,f (x )最小=f (2)=a 2. ∴a -a 2=a2.∴a (2a -1)=0,∴a =0(舍)或a =12.∴a =12.综上可知,a =12或a =32.12.函数y =lg(3-4x +x 2)的定义域为M ,当x ∈M 时,求f (x )=2x +2-3×4x 的最值. 解:由3-4x +x 2>0,得x >3或x <1, ∴M ={x |x >3,或x <1},f (x )=-3×(2x )2+2x +2=-3⎝⎛⎭⎫2x -162+2512. ∵x >3或x <1,∴2x >8或0<2x <2, ∴当2x =16,即x =log 216时,f (x )最大,最大值为2512,f (x )没有最小值.B 组1.函数f (x )=a |x +1|(a >0,a ≠1)的值域为[1,+∞),则f (-4)与f (1)的关系是( )A .f (-4)>f (1)B .f (-4)=f (1)C .f (-4)<f (1)D .不能确定解析:选A 由题意知a >1,又f (-4)=a 3,f (1)=a 2,由单调性知a 3>a 2,∴f (-4)>f (1). 2.已知函数f (x )=|2x -1|,a <b <c ,且f (a )>f (c )>f (b ),则下列结论中,一定成立的是________.①a <0,b <0,c <0;②a <0,b ≥0,c >0; ③2-a <2c ;④2a +2c <2.解析:画出函数f (x )=|2x -1|的图象(如图), 由图象可知,a <0,b 的符号不确定,c >0.故①②错;∵f (a )=|2a -1|,f (c )=|2c -1|, ∴|2a -1|>|2c -1|,即1-2a >2c -1, 故2a +2c <2,④成立; 又2a +2c >22a +c ,∴2a +c <1,∴a +c <0,∴-a >c ,∴2-a >2c ,③不成立.答案:④3.已知函数f (x )=⎝⎛⎭⎫13ax 2-4x +3. (1)若a =-1,求f (x )的单调区间; (2)若f (x )有最大值3,求a 的值.解:(1)当a =-1时,f (x )=⎝⎛⎭⎫13-x 2-4x +3, 令t =-x 2-4x +3,由于t (x )在(-∞,-2)上单调递增,在[-2,+∞)上单调递减,而y =⎝⎛⎭⎫13t 在R 上单调递减,所以f (x )在(-∞,-2)上单调递减,在[-2,+∞)上单调递增, 即函数f (x )的递增区间是[-2,+∞),递减区间是(-∞,-2).(2)令h (x )=ax 2-4x +3,f (x )=⎝⎛⎭⎫13h (x ),由于f (x )有最大值3,所以h (x )应有最小值-1,因此必有⎩⎪⎨⎪⎧a >0,12a -164a =-1,解得a =1. 即当f (x )有最大值3时,a 的值等于1.。
指数与指数函数教案一、教学目标1.了解指数的概念,掌握指数的运算法则;2.掌握指数函数的概念,了解指数函数的图像特征;3.能够应用指数和指数函数解决实际问题。
二、教学重点1.指数的概念及运算法则;2.指数函数的概念及图像特征。
三、教学难点1.指数函数的图像特征;2.应用指数和指数函数解决实际问题。
四、教学内容及方法1. 指数的概念及运算法则(1)指数的概念指数是数学中的一个概念,表示一个数的幂次。
例如,a n中的n就是指数,表示a的n次幂。
(2)指数的运算法则指数的运算法则包括:•同底数幂的乘法:a m⋅a n=a m+n;=a m−n;•同底数幂的除法:a ma n•幂的乘法:(a m)n=a mn;=a mn−k;•幂的除法:(a m)na k•负指数:a−n=1;a n•零指数:a0=1。
(3)教学方法通过讲解和例题演示,让学生掌握指数的概念和运算法则。
2. 指数函数的概念及图像特征(1)指数函数的概念指数函数是一种以指数为自变量的函数,通常写作y=a x,其中a是底数,x是指数。
(2)指数函数的图像特征指数函数的图像特征包括:•当a>1时,函数图像上升,且y轴是渐近线;•当0<a<1时,函数图像下降,且x轴是渐近线;•当a=1时,函数图像是一条水平直线。
(3)教学方法通过讲解和绘制指数函数的图像,让学生了解指数函数的概念和图像特征。
3. 应用指数和指数函数解决实际问题(1)应用指数解决实际问题指数在实际问题中的应用包括:•复利计算;•指数增长和指数衰减;•指数函数模型。
(2)应用指数函数解决实际问题指数函数在实际问题中的应用包括:•人口增长模型;•经济增长模型;•生物衰减模型。
(3)教学方法通过讲解和例题演示,让学生掌握应用指数和指数函数解决实际问题的方法。
五、教学评价教学评价包括:•学生课堂表现;•学生作业完成情况;•学生考试成绩。
六、教学反思本次教学中,我采用了讲解、例题演示和绘图等多种教学方法,让学生掌握了指数和指数函数的概念、运算法则和应用方法。
指数与指数函数一、知识讲解考点1根式的概念(1)定义:若一个数的n 次方等于),1(*∈>N n n a 且,则这个数称为a 的n 次方根.即,若a x n =,则x 称a 的n 次方根(*∈>N n n 且1).①当n 为奇数时,n a 的次方根记作na ;②当n 为偶数时,负数a 没有n 次方根,而正数a 有两个n 次方根且互为相反数,记作)0(>±a a n .(2)性质:①a a n n =)(;②当n 为奇数时,a a nn =;③当n 为偶数时,⎩⎨⎧<-≥==)0()0(||a a a a a a n n.考点2幂的有关概念(1)规定:①)(*∈⋅⋅⋅=N n a a a a n;②)0(10≠=a a ,③∈=-p a a pp (1Q ) ④m a a an m nm ,0(>=、*∈N n ,且)1>n(2)性质:①r a a a a sr sr,0(>=⋅+、∈s Q ),②r a aa sr sr ,0()(>=⋅、∈s Q ),③∈>>⋅=⋅r b a b a b a rrr,0,0()( Q )(注)上述性质对r 、∈s R 均适用.考点3指数函数定义:函数)1,0(≠>=a a a y x且叫做指数函数. a >10<a <1二、例题精析【例题1】求下列各式的值:(1)21100;(2)328; (3)239-;(4)4381-.【解析】(1)2110010=)10(=212.(2)3284=2=)2(=2323.(3)239-271=3=)3(=3232--. (4)4381-271=3=)3(=3434--. 【例题2】用分数指数幂的形式表示下列各式(>0) (1)a a3; (2)322a a ·;(3)3a a · 【解析】(1).(2)322aa ·3832+2322===a aa a .(3)3a a ·323431===a a aa .【例题3】计算:25.02121325.0320625.0÷])32.0(×)02.0(÷)008.0(+)945()833[(----. 【解析】 原式=41322132)10000625(]102450)81000()949()278[(÷⨯÷+- 922)2917(21]1024251253794[=⨯+-=÷⨯⨯+-=. 【例题4】化简:.)2(2485332332323323134aa a a ab aaab b b a a ⋅⋅⨯-÷++--a 117333222a a a aa +=⋅==【解析】原式=51312121323131231313123133133131)()(2)2()2()(])2()[(a a a a ab a b b a a b a a ⋅⋅⨯-÷+⋅+- 23231616531313131312)2(a a a a aa ba ab a a =⨯⨯=⨯-⨯-=.提示:这是一组很基本的指数运算的练习题,虽然在考试中这些运算要求并不高,但是数式运算是学习数学的基本功,通过这样的运算练习熟练掌握运算公式、法则,以及学习数式变换的各种技巧.根式运算或根式与指数混合运算时将根式化为指数式运算较为方便,对于计算的结果,不强求统一用什么形式来表示,如果有特殊要求,可根据要求写出结果,但结果不能同时含有根号和分数指数,也不能既有分母又含有负指数. 【例题5】比较下列各组数的大小(1)2277.0与 (2)32与3)21( (3)5.02与25.0 (4)3121⎪⎭⎫⎝⎛,3221⎪⎭⎫ ⎝⎛,3251⎪⎭⎫ ⎝⎛【解析】(1)由2x 在)+∞,0[上是增函数,∵7<7.0,∴227<7.0.(2)由x 2在R 上是增函数,∵3<3-,∴332<2-,即3321<2)(. (3)由x 2在R 上是增函数,∵2>5.0-,∴25.02<2-,即225.05.0=21<2)(.(4)由x )21(在R 上是减函数,∵32<31,∴3231)21(>)21(,又32x 在)+∞,0[上是增函数,∵51>21,∴3232)51(>)21(;故323231)51(>)21(>)21(.【例题6】已知函数11)(+-=x x a a x f ,)0(>a(1)判断函数的奇偶性;(2)求该函数的值域;(3)证明()f x 是R 上的增函数.【解析】(1)∵定义域为x R ∈,且11)(+-=---x x a a x f =xxaa --+-11=)(x f - ∴ )(x f 是奇函数;(2)121)(+-+=x x a a x f =121+-x a ∵1+x a >1,∴ 0<12+xa <2 即函数11)(+-=x x a a x f 的值域为)1,1(-;(3)设1x ,2x R ∈,且1x <2x ,则21x x a a<)(1x f -)(2x f =1111+-x x a a -1122+-x x a a =)1)(1(222121+--x x x x a a a a <0,∴()f x 是R 上的增函数.提示:函数的性质综合问题,需要准确把握定义域、值域、奇偶性、单调性等基本概念,充分运用数形结合、分类讨论、等价转换等数学思想,灵活运用通性通法.三、课堂运用【基础】1.求值下列各式的值:①;②;③;④【解析】① . ②. ③.2381225-51()2-3416()81-2223323338(2)224⨯====1112()21222125(5)555--⨯--====5151(5)1()(2)2322----⨯-===④.2.化简46394369)()(a a ⋅的结果为()A .a 16B .a 8C .a 4D .a 2【解析】原式=461319431619)))((()))(((a a ⋅=22a a ⋅=4a ,故选C .;【巩固】 3.若122-=xa,则xx xx a a a a --++33等于()A .22-1B .2-22C .22+1D .2+1【解析】注意到122+=-xa.∴xx x x aa a a --++33=x x x x a a a a --++33)()(=x x x x x x a a a a a a ---++-+)1)((22 =x x a a 221-+-=122-.选A .4.在下列图象中,二次函数c bx ax y ++=2与函数x aby )(=的图象可能是()【解析】由函数x aby )(=知ab >0,于是抛物线c bx ax y ++=2的对称轴应在y 轴左边,B 、D 两个答案被排除.对于答案C ,显然12-=-a b ,a b =2,函数x aby )(=为增函数,图象与之不符,被淘汰.故选A .提示:从图象看,c =0,关键由a 与b 大小决定.重要的条件是指数函数x ab y )(=的底a b >0,使得对称轴与x 轴的交点横坐标a b 2-<0.再由0<a b <1,便定出ab 2-的位置. 334()344162227()()()81338-⨯--===lg10==【拔高】5.设5.1344.029.01)21(,8,4-===y y y ,则()A .3y >1y >2yB .2y >1y >3yC .1y >2y >3yD .1y >3y >2y【解析】化为同底,再利用单调性即可.∵8.112=y ,32.122=y ,5.132=y ,又∵函数xy 2=是单调增函数,∴1y >3y >2y ,故选D .6.求函数y =3322++-x x的定义域、值域和单调区间.【解析】(1)定义域显然为(-∞,+∞).(2)∵ 4)1(423)(22≤--=-+==x x x x f u , ∴ uy 3=是u 的增函数,∴4330≤<u ,即函数的值域为]81,0(.(3) 当x ≤1 时,u =)(x f 为增函数,uy 3=是u 的增函数,y 由x ↑→u ↑→y ↑∴原函数单调增区间为(-∞,1];当x >1时,u =)(x f 为减函数,u y 3=是u 的增函数,由x ↑→u ↓→y ↓∴原函数单调减区间为[1,+∞).提示:这是复合函数的典型例子.是指数函数与二次函数的复合,由于外层指数函数u y 3=是u 的增函数,所以该函数的单调性由内层函数也就是二次函数223)(x x x f u -+==决定.另一类由基本初等函数经过四则运算而形成的函数,其单调性和奇偶性的判定需采用前面所学办法.四、课程小结(1)指数运算常规方法将小数化为分数,带分数化为假分数,负指数化为正指数,根指数化为分数指数.(2)1,0≠>a a 时,xa y -=与xa y =的图象关于y 轴对称,即x ay )1(=与xa y =的图象关于y 轴对称.(3)指数函数都以x 轴为渐近线(当10<<a 时,图象向左无限接近x 轴,当1>a 时,图象向右无限接近x 轴). (4)比较大小问题的处理方法①看类型 ②化为同底用单调性 ③其它类型找中间量. (5)复合函数的单调性对于复合函数的单调性,可以根据各层函数单调性去判别.五、课后作业【基础】1.求值(1)2325(2)21)425(-(3)41)0081.0(-【解析】(1)125=5=)5(=25323223;(2) 52=)25(=])25[(=)425(121221---;(3) 310=)103(=)1000081(=)0081.0(14141---; 2.指数函数xa x f )1()(2-=是减函数,求实数a 的取值范围. 【答案】)2,1()1,2( --.3.已知指数函数xa x f =)((>0且≠1)的图象过点(3,π),求【解析】由π=)3(f ,得π=3a ,即31=πa ,3=)(x x f π,∴1==)0(0πf ;331==)1(ππf ;ππ1==)3(1--f . 4.求函数151-=xy 的定义域.a a (0),(1),(3)f f f -的值.【答案】)+∞,0( 【巩固】1.计算下列各式(式中字母都是正数)(1); (2). 【解析】(1)原式===4;(2)原式==. 2.计算下列各式(1)(2>0).(1)原式====;(2)原式=.3.已知44221)31)(21(,31aa aa aa a a aa +++++=+求的值.【解析】719)1(312=+⇒=+⇒=+aa aa aa , 47149)1(222=+⇒=+∴aa a a ,])())[((1221212122121212323a aa a a a aa aa a a +⋅-+=+=+∴---211511336622(2)(6)(3)a b a b a b -÷-31884()m n -211115326236[2(6)(3)]ab+-+-⨯-÷-04ab a 318884()()m n -23m n -2(a 111324(25125)25-÷231322(55)5-÷2131322255---1655-5125222362132a aa a a--===⋅1863)11)(1(=⨯=+-+=a a aa ,而512)1(124444=++=+=+aa aa aa ,5200550205)347()218(=⨯=+⨯+=∴原式.4.函数xa y =在]1,0[上的最大值与最小值的和为3,则=a .【答案】=a 2; 5.函数y =121+x 的值域是_____. 【答案】(0,1)【拔高】1.若∈n N *,则=+-+++----12412411n n nn ()A .2B .n-2C .n-12D .n22-【答案】A2.下列各式中正确的是( )【解析】由x y )21(=是减函数,得32)21(<31)21(,答案B 、C 被淘汰.又32)51(<32)21(,故选D .3.函数()xa y 1-=与x a y ⎪⎭⎫ ⎝⎛=1具有不同的单调性,则()311-=a m 与31⎪⎭⎫⎝⎛=a n 的大小关系是()A .m <nB .m =nC .m >nD .不能确定A B C D .<<.<<.<<.<<()()()()()()()()()()()()12151212121515121215121223231313232323132323231311【解析】⇒<<⇒⎩⎨⎧<<<⇒⎪⎩⎪⎨⎧><-101021111a a a aa m <n ; 或⇒>⇒⎩⎨⎧>>⇒⎪⎩⎪⎨⎧<<>-21211011a a a a a m >n .故选D . 4.已知函数2)(x x e e x f --=,2)(xx e e x g -+= (1)判断函数)(x f 、)(x g 的奇偶性;(2)证明()f x 是R 上的增函数;(3)证明:①)2(x f =2)(x f )(x g ;②1)]([)]([22=-x f x g .【解析】(1)(略))(x f 为奇函数,)(x g 为偶函数;(2)x e 是R 上的增函数,x e -是R 上的减函数,∴()f x 是R 上的增函数; (3)证明:①)2(x f =222xx e e --, 2)(x f )(x g =222x x x x e e e e --+⋅-=222xx e e --, ∴ )2(x f =2)(x f )(x g ;②22)]([)]([x f x g -=22]2[]2[xx xx e e e e ----+ =42422222-+-++--x x x x e e e e =1.。