计算材料学第三章原子间相互作用势
- 格式:pdf
- 大小:1.37 MB
- 文档页数:36

第三章探索原子构建物质的奥秘 3.1 原子间的相互作用由量子化学从头计算方法得出不同距离时两个原子间的相互作用能,以势能曲线最低点与量子化学从头计算的最小值相重合的拟合原则,拟合出原子间相互作用对势。
并尝试用原子间相互作用对势研究铁团簇(奥氏体、铁素体和马氏体)的原子平均结合能和最近平衡原子间距。
计算结果表明,这种近似方法对理解金属晶体的相变和许多性能可以提供证据。
如此推断,可以计算Fe-Cr-Mn-C-B系复杂合金的奥氏体的能量变化,并为解释相变的趋势提供参考。
关键词:原子间相互作用势;量子化学从头计算;拟合对势;铁团簇 1.引言由第一性原理量子力学所作的计算可以给出精确的结果。
然而,由于需要很大的计算量来精确求解Schrödinger方程,目前这些方法仅限于研究包含几十个原子的体系。
原子间相互作用势是分子动力学、蒙特卡罗方法模拟计算的基础,也是在原子、分子层次上进行合金设计的重要部分。
原子间相互作用势有很多种,按相互作用的类型划分为两体势(即对势、偶对势)、三体势、四体势、N 体势、嵌入原子势等。
物质(包括各种相,如固相、液相和气相)的许多物理性质既可以通过实验观察和测定,也可以在理论上计算和预测。
另一方面,经验的原子间相互作用势虽不及上述方法精确,但能处理大得多的体系。
对于复杂的材料科学问题的计算机模拟,原子间相互作用势及分子动力学方法占有重要地位[1]。
本文尝试用原子间相互作用对势研究奥氏体、铁素体和马氏体铁团簇的原子平均结合能和最近平衡原子间距,为进行Fe-Cr-Mn-C-B系实用合金的复杂体系的特性的预测提供参考。
2.原子间相互作用对势原子间相互作用对势的简单函数是Lennard-Jones势。
尽管Lennard-Jones型函数仅仅可以用来描述多体势作用最小的稀有气体,而对于象金属晶体这样多体势作用强的晶体被认为是不适用的,但是,作为对复杂体系合金的初步探讨,这种方法很可能对理解许多性能和过程可以提供有益的参考。

一、知识梳理(C)物质的硬度差异,在生产、生活、科研中有着广泛的应用(D)金刚砂(SiC)和金刚石具有同样的硬度【解析】A正确,因为指明是天然的。
B正确,相信随着科学技术的不断发展,一定会有新物质被制备出来。
C正确,可以举出许多例子。
D错,据目前报道,硬度大于金刚石的只有氮化碳。
金刚砂的硬度仅次于金刚石。
故选D。
【答案】D【例2】已知乙酸分子的结构可表示为,下列说法正确的是( )(A)氢原子与氢原子之间存在化学键(B)碳原子与碳原子之间存在化学键(C)氧原子与氧原子之间存在化学键(D)乙酸分子之间存在化学键【解析】由于乙酸是由分子构成的物质,在乙酸的分子内只有相邻的原子之间存在化学键,不相邻的原子同就不存在化学键。
但在乙酸的分子与分子之问是由微弱的范德华力结合,范德华力比化学键的能量小得多。
【答案】B【例3】已知水的分解温度高于1 800℃多,难以分解的原因是________________________。
【解析】由于水分子内氢、氧原子之间存在强烈的相互作用——共价键(如图中的实线部分),所以要破坏氢、氧原子间的共价键,就需要吸收很多的能量,才能使其分解成为H2和O2,因而分解温度很高,需要超过1800℃。
但水分子与水分子之间,存在较弱的相互作用力——氢键(如图中的虚线部分),因此要使水蒸发成为水蒸气,只须破坏氢键及范德华力即可,所需能量较小,所以水的沸点是100℃。
【答案】见解析。
【例4】已知二氧化碳和二氧化硅( SiO2)组成相近,二氧化硅俗称石英。
水晶是一种纯度较高的二氧化硅晶体,试从物理性质上分析两者的差异,思考为什么组成相近的物质性质也有那么大的差异。
【解析】二氧化碳是我们熟悉的物质,所以在对比时不难得出结论。
但关键在如何作全面的对比分析,借助我们平时研究物质的物理性质时的规律,从色、态、味,溶解性、熔、沸点着手,就可以发现它们的反差很大,所以用途也完全不同。
组成相近并不代表组成的物质结构相同,所以物质的性质是由多方面因素综合决定的。






晶体的结合能、内能、原子间相互作用势能之间的区别晶体是由大量原子或分子组成的固体材料,它具有一定的结构和周期性,具有一定的热力学性质。
在研究和理解晶体性质的过程中,结合能、内能和原子间相互作用势能是重要的概念。
它们之间存在着一些区别和联系,接下来我将详细介绍这三个概念。
首先,我们来讨论结合能。
结合能是指晶体中各个原子之间的结合程度。
它代表了形成或破坏一个晶体所需要的能量。
结合能的大小可以反映晶体的稳定性和强度。
在晶体中,原子或分子之间通过化学键来相互结合,形成晶体的稳定结构。
不同类型的物质有不同的结合方式,例如离子晶体是通过离子键相互结合,而共价晶体是通过共价键相互结合。
结合能可以通过实验或计算方法来确定,它通常以能量的形式表示,单位为焦耳或电子伏特。
其次,我们来谈谈内能。
内能是指晶体中各个原子或分子的总能量。
它包括晶格振动能、电子能和其他能量形式。
晶体的内能与其温度和压力有关。
在晶体中,原子或分子通过振动和相互作用来形成晶格结构。
晶格振动能是晶体中原子或分子振动的能量,它与温度相关,随着温度的升高而增加。
电子能是晶体中电子的能量,它与原子或分子内部的电子分布和电子运动状态有关。
除了晶格振动能和电子能,晶体中还可能存在其他能量形式,例如电磁能、磁能等。
内能可以通过实验或计算方法来确定,它通常以能量的形式表示,单位为焦耳或电子伏特。
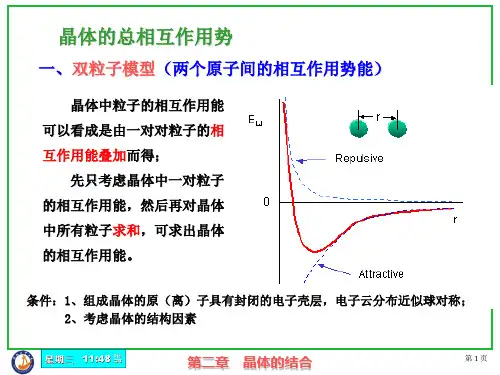
最后,我们来探讨原子间相互作用势能。
原子间相互作用势能是指晶体中相邻原子或分子之间相互作用的能量。
它描述了晶体中原子或分子之间的相互作用强度和性质。
在晶体中,原子或分子之间的相互作用可以通过势能函数来描述,其中吸引势能和排斥势能是两个主要成分。
吸引势能是由于原子或分子之间的吸引力而产生的,它使得晶体能够形成稳定的结构。
排斥势能是由于原子或分子之间的排斥力而产生的,它使得晶体中原子或分子之间保持一定的距离。
原子间相互作用势能可以通过实验或计算方法来确定,它通常以能量的形式表示,单位为焦耳或电子伏特。

第三章晶体热振动与晶体的热学性质3。
1一维单原子链3。
1。
1一维原子间相互作用势图 3—1-1 一维单原子晶格考虑由N 个相同的原子组成的一维晶格,如图 3-1-1 所示,相邻原子间的平衡距离为 a ,第 j 原子的平衡位置用x0j来表示,它偏离平衡位置的位移用 u j来表示,第 j 原子的瞬时位置就可以表示为:(3-1-1)原子间的相互作用势能设为,如果只考虑晶体中原子间的二体相互作用,则晶体总的相互作用能可表示为:(3-1—2)式中是 i 、 j 原子的相对距离,是 i , j 两原子的相对位移,在温度不太高时,原子在平衡位置附近作微振动,相邻原子的相对位移要比其平衡距离小得多,可将展开为:(3-1—3)于是有:(3—1-4)式中第一项是所有原子处于平衡位置上时的总相互作用能,用 U 0来表示,是 U 的极小值,(3-1—5)第二项是的线性项,它的系数为: ,是所有其它原子作用在 i 原子的合力的负值,当所有原子处在平衡位置上时,晶体中任一原子所受到的净作用力应为零,所以在式( 3-1-4 )中不存在位移的线性项。
因此,(3-1-6)式中:(3-1—7)称为力常数。
3。
1。
2 简谐近似下运动方程若在 U 的展开式中,忽略 u 的高次项而仅保留到 u 的平方项,即有(3—1—8)这种近似称为简谐近似。
由此可以得出第 n 原子的运动方程式为:(3-1-9)式中 m 为原子的质量,如果只考虑最近邻的相互作用,在上式中只保留i=n+ 1 和i = n —1 两项,且令,则可得到形式上很简单的运动方程式:(3-1-10)3。
1.3 周期性边界条件对于无限大的晶体,每个原子都有形如式( 3-1—10 )的运动方程,但实际上晶体是有限大的,处在表面上(对一维晶格来说是两端上)的原子所受到的作用与内部原子不同,其运动方程式应有不同,使问题变复杂.为解决这一问题,需要引入边界条件,常用的边界条件是所谓的周期性边界条件,是玻恩—卡曼提出的,又称为玻恩 - 卡曼边界条件。
原子间引力公式范文引力是自然界中最重要的基本力之一,它对我们的生活和科学研究有着重要的影响。
通过研究原子间引力,我们可以了解和解释物质的结构和性质。
在本文中,我将详细讨论原子间引力的公式以及其应用。
首先,我们需要了解原子间引力的概念。
原子间引力是指两个或多个原子之间的相互作用力,这种力的大小取决于原子之间的距离和它们之间的性质。
原子间引力是由于原子之间的静电相互作用而产生的,其中正电荷与负电荷相吸引,正电荷与正电荷或负电荷与负电荷相斥。
这种引力决定了原子的排列方式和物质的物理性质。
F=k(q1*q2)/r^2其中,F表示引力或斥力的大小,k是库仑常数,q1和q2是两个原子上的电荷,r是两个原子之间的距离。
库仑定律指出,原子间引力与电荷的乘积成正比,与两个原子之间的距离的平方成反比。
这意味着,如果两个原子上的电荷增加,它们之间的引力也会增加;如果两个原子之间的距离增加,它们之间的引力会减小。
这个公式的应用非常广泛,不仅可以用来描述原子间引力,还可以用来描述分子间引力、电场、介质的极化等现象。
它为我们解释物质的性质和现象提供了重要的数学工具。
然而,实际情况并非总是简单的,有时我们需要考虑更多的因素来描述原子间引力。
例如,当原子之间存在电荷分布不均匀、极化效应或多极相互作用时,库仑定律需要进行修正。
这些修正包括使用多项式来描述电荷分布、引入极化能量项等。
除了库仑定律之外,还有其他描述引力的公式。
例如,范德瓦尔斯力是一种描述非极性分子或原子之间引力的常见公式,它可以用以下公式表示:F=-(A/r^6)+(B/r^12)其中,F表示引力的大小,A和B是与分子之间的极化和形状相关的常数,r是分子之间的距离。
范德瓦尔斯力公式是原子间引力研究的重要工具,它可以解释很多实际问题,如液体的表面张力、气体的相变等。
总之,原子间引力是一种重要的相互作用力,它决定了物质的结构和性质。
库仑定律和范德瓦尔斯力公式是描述原子间引力的常用公式,它们为我们研究和理解物质的行为提供了重要的数学工具。