相互作用势

分子间的相互作用势能与分子力罗兴垅【摘要】引入相对距离R、相对势能U与相对力F,导出了米势的相对势能U（R）及其相应的相对力F（R）与参数n、m的关系,并精确地绘制了伦纳德-琼斯势的相对势能U（R）曲线及其相应的相对力F（R）曲线和平衡位置附近的近似相对势能U（X）曲线、近似相对力F（X）曲线.%The paper introduces the relative distance,relative potential energy and relative power,derives the relative potential energy of Mie potential and its corresponding relative force and the relationships of parameter n and m,and accurately draws the relative potential energy curve of Leonard-Jones potential and its corresponding relative force curve and near the equilibrium position the approximate relative potential energy curve and the approximate relative force curve.【期刊名称】《赣南师范学院学报》【年(卷),期】2012(033)006【总页数】6页(P57-62)【关键词】米势;雷纳德—琼斯势;相对距离;相对势能;相对力【作者】罗兴垅【作者单位】赣南师范学院物理与电子信息学院,江西赣州341000【正文语种】中文【中图分类】O552物质由分子(或原子)组成，分子热运动和分子间的相互作用是决定物质各种热学性质的基本因素.分子间相互作用的关系很复杂，无法由实验直接测定，从理论(即使是量子理论)上也不容易得到一般性的解决，很难用简单的数学公式表示出来，通常采取的办法是在实验基础上采用简化模型来处理问题［1］.一种常用的模型是假设分子间的相互作用具有球对称性，1907年米(Mie)指出，分子或原子间相互作用势为其中α＞0，β＞0，n＞m ＞0，它们是通过实验确定的常数.式中第一项为排斥势，第二项为吸引势，且排斥势作用半径比吸引势作用半径小，式(1)简称为米势［2］. 在多数情况下，取m=6，n为9～12之间的整数，而以n=12为最佳［3］.1924年，伦纳德－琼斯(Lennard-Jones)又提出了半经验公式式中u0是在平衡位置(r=r0)时的势能的绝对值.式(2)简称为伦纳德－琼斯势［4］. 由于米势、伦纳德－琼斯势中均有一对参数(两种表式分别为α、β或u0、r0)是待定的，与物质有关，对于米势还需选定n、m的值.因此，热学、热力学与统计物理学和固体物理学教材［1－9］一般仅绘制定性的分子势能曲线与分子力曲线.本文探讨米势的相对势能U及其相应的相对力F与参数n、m的关系，并以雷纳德—琼斯势为例，精确地绘制分子势能曲线与力曲线.1 米势1.1 米势由式(1)，可得两分子间的相互作用力在平衡位置r0处，分子所受的力为零.令f(r0)=0，可解得式(4)代入式(1)得在平衡位置r0处，势能为u(r0)，由上式有代入式(6)得由上式可知，米势由四个参数(u0、r0、n、m)确定.若给定某种分子的四个参数(u0、r0、n、m)值，则可绘制该种分子的势能曲线.当时，u(σ)=0，排斥势与吸引势的绝对值相等，且等于根据式(9)、式(10)，可将式(8)改写成如下形式u(r)对r的一阶、二阶导数分别为由式(12)、(13)可知，在平衡位置r0处，势能有极小值u(r0)=－u0，势能曲线拐点位于由上述讨论可知米势的势能曲线特征为：（Ⅰ）当r→0时，u(r)→ +∞;当r→ +∞ 时，u(r)→0;在平衡位置r0(＞σ)处，势能有极小值u(r0)=－u0.（Ⅱ）当0＜r≤σ时，u(r)≥0;当σ ＜r＜+∞ 时，u(r)＜0.（Ⅲ）当0＜r≤r0时，即势能随r的增大而减小;当r0＜r＜+∞ 时，即势能随r的增大而增大.（Ⅳ）势能曲线拐点位于δ(＞r0)处，当0＜r＜δ时，曲线是凹的;当δ＜r＜+∞ 时，曲线是凸的.1.2 米势的相对势能令相对距离R=r/r0，相对势能U(R)=u(R)/u0，则式(8)变为上式表示米势的相对势能仅由二个参数(n、m)确定，与参数(r0、u0)无关.只要给定参数n、m的值，就可以绘制一类分子的相对势能曲线.1.3 米势的近似相对势能在讨论固体、液体中分子的热振动以及固体的热膨胀时，需要知道分子在平衡位置附近的势能曲线形状.为此，将米势u(r)在平衡位置r=r0处(即令r=r0+x)展开成泰勒级数式(8)对r的零阶、一阶、二阶与三阶导数在平衡位置r=r0处的值分别为代入米势u(r)的展开式，并保留到第四项，得上式为米势u(r)的近似式，其成立条件为x≪r0.若令相对距离X=x/r0，相对势能U(X)=u(x)/u0，则式(17)可改写为上式为米势u(r)的近似式，其成立条件为X≪1.若保留到第二项，则势能曲线为抛物线，分子应在平衡位置附近作简谐振动;若保留到第三项，则势能曲线不是抛物线，势能曲线在平衡位置附近不再对称，分子将在平衡位置附近作非简谐振动.1.4 米势的分子力式(4)代入式(3)得令 f0斥=mαr－(m+1)0 ，并由式(7)可得它是平衡位置r0处分子受到的斥力.于是，与米势相应的分子间的相互作用力为当r=r0时，f(r0)=0，排斥力与吸引力的大小相等.由(13)式可知，势能曲线拐点对应于力曲线的“极小值”令，可得力曲线拐点由上述讨论可知米势的力曲线特征为：（Ⅰ）当r→0时，f(r)→ +∞;当时r→ +∞，f(r)→0;在r=δ(对应于势能曲线拐点)处，f(r)有极小值.（Ⅱ）当0＜r≤r0时，f(r)≥0;当r0＜r＜+∞ 时，f(r)＜0.（Ⅲ）当0 ＜r≤ δ时，即f(r)随r的增大而减小;当δ＜r＜+∞ 时，即f(r)随r的增大而增大.（Ⅳ）力曲线拐点位于λ(＞δ)处，当0＜r＜λ时，曲线是凹的;当λ＜r＜+∞ 时，曲线是凸的.1.5 米势的相对分子力令相对距离R=r/r0，相对力F(R)=f(r)/f0斥，则式(20)变为上式表示米势的相对力仅由二个参数(n、m)确定，与参数(r0、u0)无关.只要给定参数n、m的值，就可以绘制一类分子的相对力曲线.1.6 米势的近似相对分子力由式(17)，可得米势的近似分子力为令相对距离X=x/r0，相对分子力F(X)=f(x)/f0斥，则式(24)可改写为(24)式与(25)式的成立条件均为X≪1.2 伦纳德—琼斯势2.1 伦纳德—琼斯势当米势中的m=6、n=12时，米势即为伦纳德－琼斯势令式(8)中的m=6、n=12，上式变为式(2)的形式令式(10)、式(11)中的m=6、n=12，则u斥(σ)=4u0，伦纳德－琼斯势可写成如下形式2.2 伦纳德—琼斯势的相对势能曲线令式(15)中的m=6、n=12，可得伦纳德－琼斯势的相对势能为根据上式，使用数学软件Matlab绘制雷纳德－琼斯势的相对势能曲线以及排斥势、吸引势的相对势能曲线，如图1所示.相对势能曲线是不对称的，平衡位置(R=1)的左边较陡，右边较平坦，势能曲线拐点位于R=1.108 7 处.图1 实线为雷纳德－琼斯势的相对势能曲线(右图中的上、下虚线分别为排斥势、吸引势的相对势能曲线)2.3 伦纳德—琼斯势的相对分子力曲线令式(20)中的m=6、n=12，可得伦纳德－琼斯势的分子力为式中f0斥=12u0/r0是平衡位置r0处分子受到的斥力.令式(23)中的m=6、n=12，可得伦纳德－琼斯势的相对分子力为根据上式，使用数学软件Matlab绘制雷纳德－琼斯势的相对力曲线以及排斥力、吸引力的相对力曲线，如图2所示.相对力曲线也是不对称的，平衡位置(R=1)的左边较陡，右边较平坦，力曲线拐点位于R=1.217 1 处.图2 实线为雷纳德－琼斯势的相对力曲线(右图中的上、下虚线分别为排斥力、吸引力的相对力曲线)表1 部分气体的参数值气体 He H2 Ne Ar Kr N2 O2 CO2 6 0.448 6 r0/nm0.295 2 0.322 2 0.312 1 0.382 2 0.404 1 0.415 1 0.388 4 0.503 6 u0/10 －20J 0.008 321 0.040 30 0.048 16 0.165 3 0.236 0 0.131 2 0.162 8 0.260 8 δ/nm 0.327 3 0.357 2 0.346 0 0.423 8 0.448 0 0.460 2 0.430 6 0.558 3 f(δ σ/nm 0.263 0.287 0.278 0.340 5 0.360 0.369 8 0.34 503 1 0.621 6)/10 －10N 0.007 586 0.033 66 0.041 54 0.116 4 0.157 2 0.085 04 0.112 8 0.139 4 f0斥 /10 －10N 0.033 82 0.150 1 0.185 2 0.519 1 0.700 8 0.379 2 0.根据文献［8］提供的气体参数u0(平衡位置的势能的大小)和σ(排斥势与吸引势的绝对值相等点)的值，利用关系式可计算出平衡位置r0、f(r)的极值点0.224 16)，平衡位置处分子受到的斥力f0斥的值，见表1.2.4 伦纳德—琼斯势的近似相对势能曲线令式(18)中的m=6、n=12，可得伦纳德－琼斯势在平衡位置附近的近似相对势能为其成立条件为X≪1.由它所绘制的雷纳德－琼斯势的近似相对势能曲线如图3中的实线所示.从图3可知，近似的相对势能曲线也是不对称的，平衡位置(X=0)的左边较陡，右边较平坦.2.5 伦纳德—琼斯势的近似相对分子力曲线令式(25)中的m=6、n=12，可得伦纳德－琼斯势在平衡位置附近的近似相对力为由它所绘制的绘制雷纳德－琼斯势的近似相对力曲线如图4中的实线所示.若略去式(32)的第二项，则近似相对力为线性恢复力，其相对力曲线如图4中的虚线所示.由图4可看出，恢复力在平衡位置两边也不对称.当X＞0时，恢复力比线性关系所预期的值小，则当X＜0时，恢复力比线性关系所预期的值大.即两分子间距增大时，吸引力比线性关系所预期的值小，两分子间距减小时，斥力比线性关系所预期的值大.图3 雷纳德－琼斯势的近似相对势能曲线(虚线为抛物线，对应于势能U(X)=－1+36X2)图4 雷纳德－琼斯势的近似相对力曲线(虚线为直线，对应于线性力F(X)=－6X) 本文引入相对距离R、相对势能U与相对力F，导出了米势的相对势能U(R)及其相应的相对力F(R)与参数n、m的关系，并精确地绘制了伦纳德－琼斯势的相对势能U(R)曲线及其相应的相对力F(R)曲线，形象直观准确地显示了它们的变化规律，弥补了热学、热力学与统计物理学和固体物理学教材中仅给出定性的势能曲线与力曲线的不足.结合文献［8］提供的气体参数u0和σ(r0=)的值，可得出一幅直观、清晰、定量的气体分子间势能u或分子力f随分子间距r变化的图像.另外，还导出平衡位置附近的近似相对势能U(X)，相对力F(X)表达式，精确地绘制了伦纳德－琼斯势的近似相对势能曲线、相对力曲线.用简谐近似的方法(F≈－6X)，可解释固体的比热问题.若计入非简谐效应(F≈－6X+63X2)，可定性或定量［10］解释固体的热膨胀现象.【相关文献】［1］黄淑清，聂宜如，申先甲.热学教程［M］.第2版.北京：高等教育出版社，1994：180－185.［2］秦允豪.普通物理学教程热学［M］.第3版.北京：高等教育出版社，2011：34－44. ［3］李洪芳.热学［M］.第2版.北京：高等教育出版社，2001：6－10.［4］汪志诚.热力学·统计物理［M］.第2版.北京：高等教育出版社，1993：335－336.［5］李椿，章立源，钱尚武.热学［M］.北京：高等教育出版社，1978：59－63.［6］常树人.热学［M］.天津：天津大学出版社，2001：89－95.［7］张玉民.热学［M］.第2版.北京：科学出版社，2006：6－9.［8］梁希俠，班士良.统计热力学［M］.第2版.北京：科学出版社.2008.114－115.［9］蒋平，徐至中.固体物理学简明教程［M］.上海：复旦大学出版社.2000.93－96.［10］夏清华.含x2项非线性振子运动的研究［J］.大学物理2005，24(4))：6－7.。

对势能相互作用参数在物理学和化学中，势能相互作用参数被广泛应用于描述原子、分子和化学键之间的相互作用。

这些参数是非常重要的，因为它们能够提供有关分子结构、动力学行为和化学反应的关键信息。

本文将详细介绍势能相互作用参数的概念、应用和意义。

首先，我们来了解一下什么是势能相互作用参数。

简单来说，势能是物体在某个位置上具有的能量。

而势能相互作用参数则是用来描述两个或多个物体之间相互作用的能量参数。

这些参数可以通过不同的方法获得，例如实验测量、理论计算或者通过拟合实验数据得到。

势能相互作用参数在化学和材料研究中占据重要地位。

例如，在分子模拟中，势能相互作用参数被用来计算分子系统中不同原子之间的相互作用能量。

这些参数能够帮助我们研究分子的结构和性质，预测分子的运动和行为，并且模拟和模拟化学反应。

势能相互作用参数也用于分子力学、分子动力学和蒙特卡洛模拟等领域。

势能相互作用参数的选择和开发是一个复杂的过程。

由于不同分子系统和化学键的特性差异，合适的势能相互作用参数应该能够准确地描述系统的物理特性。

为了得到准确可靠的参数，通常需要进行大量的实验数据收集和计算模拟。

此外，优秀的势能相互作用参数应该考虑到分子的电子结构、键长、键角、键扭度等影响分子特性的因素。

势能相互作用参数在实际应用中有着广泛的意义。

首先，它们为科学家们提供了一个深入研究和理解分子结构、物质性质和化学反应机制的关键工具。

通过合理选择和优化势能相互作用参数，科学家们能够模拟和预测分子体系的性质和行为，进而指导实验设计和新材料开发。

其次，势能相互作用参数在计算化学和计算材料学领域起着至关重要的作用。

比如，通过建立基于计算的模型和方法，科学家们能够在计算上替代部分实验过程，节约时间和成本，并为实验提供指导。

最后，势能相互作用参数也为学术界和工业界之间的合作提供了桥梁。

通过共享和比较参数数据，不同机构和领域的研究人员能够相互交流、合作和互补，加快科学研究和技术发展的进程。

高熵合金相互作用势-概述说明以及解释1.引言1.1 概述高熵合金是一种新型的材料，其特点在于其成分中包含了多种原子种类，并且这些原子的摩尔比例相当接近。

相比传统合金而言，高熵合金具有更高的熵值，因此也被称为高熵合金。

由于其特殊的组织结构和化学成分，高熵合金拥有一系列优异的性能，如优异的强度、硬度和耐腐蚀性能。

高熵合金相互作用势是指描述高熵合金中各种原子相互作用的势能函数。

由于高熵合金的特殊组成，其相互作用势的选择与优化对于材料的性能和稳定性具有重要影响。

通过精确地描述原子之间的相互作用，可以更好地理解高熵合金中的晶体结构、热力学性质以及相变行为。

研究高熵合金相互作用势的重要性主要体现在以下几个方面：首先，相互作用势的准确描述是理解高熵合金的物理特性和稳定性的基础。

只有深入了解原子之间的相互作用，才能准确预测高熵合金的结构和性能。

其次，通过优化相互作用势，可以进一步改善高熵合金的性能，例如提高其强度和韧性。

最后，高熵合金相互作用势的研究也为其他领域的材料研究提供了重要的参考和借鉴，例如在催化剂和电池材料等方面的应用。

本文将重点介绍高熵合金相互作用势的定义、相关研究现状以及未来的发展方向。

通过对相互作用势的深入研究和优化，将有助于进一步提高高熵合金的性能，拓展其在材料科学和工程中的应用领域。

1.2文章结构1.2 文章结构本文将按照以下顺序介绍高熵合金相互作用势的相关内容：1. 简介：首先，将对高熵合金的定义及其特点进行简要介绍，以便读者对高熵合金的基本概念有所了解。

2. 相互作用势的重要性：接下来，将重点论述高熵合金相互作用势的重要性。

通过对高熵合金的相互作用势的深入研究，可以为高熵合金的设计和制备提供理论依据，并推动高熵合金领域的发展。

3. 研究现状：在论述高熵合金相互作用势的重要性后，将介绍当前高熵合金相互作用势研究的现状。

通过综述已有的研究成果和方法，读者可以了解高熵合金相互作用势研究的进展，并对其前沿领域有所了解。

分子动能分子势能
分子动能是指分子在运动过程中所具有的能量，是由于分子的运动而产生的能量。

分子动能与分子的质量和速度有关，可以用以下公式来计算：
动能 = 1/2 ×质量 ×速度²
其中，质量表示分子的质量，速度表示分子的速度。

分子势能是指分子所具有的势能，是由于分子之间的相互作用而产生的能量。

分子势能与分子之间的相互作用势能有关，可以用以下公式来计算：
势能 = 距离 ×相互作用势能函数
其中，距离表示分子之间的距离，相互作用势能函数表示描述分子之间相互作用的函数。

需要注意的是，势能函数与具体的分子之间的相互作用有关，因此不同分子的势能函数可能不同。

一、势能定理的准确表述1、推导如图所示，两个物体组成一个孤立系统，它们彼此存在相互作用的保守力，则由动能定理，有1：2221111122W mv mv '=-2：2212221122W mv mv '=-两式相加，有2222211212121111()()2222W W mv mv mv mv ''+=+-+由能量守恒，可知系统势能增量为2222p k 12121111()()2222E E mv mv ''∆=-∆=+-+则有2112p W W E +=-∆2、表述由上述推导可以看出，势能定理的准确表述是：物体间的相互作用保守力的总功，等于这些物体组成的系统的势能的变化的相反数，即pW E =-∆总而不是像高中课本和大部分高中资料表述的那样：重力对物体做的功，等于物体的重力势能的变化的相反数；电场力对电荷做的功，等于电荷电势能变化的相反数。

原则上讲，这些表述犯了两重错误，其一是势能属于相互作用的物体系统，而不是其中的某个物体，其二是等式的左边是相互作用力的总功，而不是其中一个力的功。

二、高中物理中势能定理的特例及其适用条件1、重力势能如右图所示，设想一个小球m 和地球M 组成一个孤立系统，两者原来均静止，现让两者在相互的万有引力作用下运动起来，则由动量守恒，有120mv Mv =-由此可知，两物体的位移满足120mx Mx =-则相互作用的万有引力（设物体在地球表面附近，且相对地球运动距离不大，万有引力可视为恒力）对两物体做的功分别为m ：11W mgx =M ：22W mgx =则系统重力势能的变化量为p 1212()()E W W mg x x mg h∆=-+=-+=-∆其中12h x x ∆=+，即两者的相对位移，或者说以地球为参考系时物体的竖直位移。

从上述分析来看，重力对m 的功，并不等于系统重力势能的变化；但是，我们通常研究的对象的质量m 远小于地球的质量M ，由120mx Mx =-可知，地球可视为几乎不动，121h x x x ∆=+≈，则有p 11E mg h mgx W ∆=-∆≈-=-这就是高中物理教材和大部分资料里面的势能定理——它成立的条件是：m M <<。

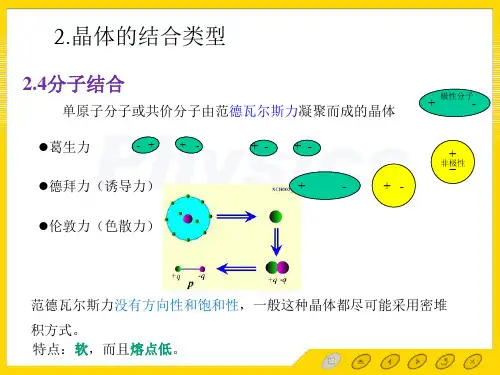
3.3几种典型晶体的结合分散的原子相互结合成晶体的根本原因在于这些原子结合起来后整个系统具有更低的能量。

在结合过程中，有一定的能量W 释放出来，称为晶体的结合能。

如果以分散的原子作为计量相互作用势能的零点，则 -W 就是结合成晶体后系统的相互作用势能。

各种不同的晶体，其结合力的类型和大小是不同的。

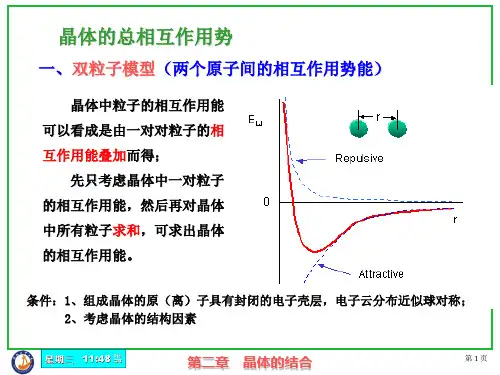
但是在任何晶体中，两个原子之间的相互作用力或相互作用势与它们之间距离的关系在定性上是相同的。

晶体中原子的相互作用可以分为两大类，即吸引作用和排斥作用。

吸引作用是异性电荷之间的库仑引力，排斥作用是由于同性电荷之间的库仑斥力和泡利原理引起的排斥。

在某一适当的距离，两种力平衡，晶格处于稳定状态。

两个原子的相互作用势能通常可以用幂函数描述：()n m rBr A r u +-= (3.3.1)此处r 为两个原子之间的距离，A, B, m, n 皆为大于零的常数，第一项表示吸引能，第二项表示排斥能。

由势能u (r )可以计算相互作用力：()()drr du r f -= (3.3.2)图3.3.1 两个原子之间的相互作用力或相互作用势与它们之间距离的关系相互作用力为零时晶格最稳定，由此可以决定原子之间的平衡距离r 0：()00=⎪⎭⎫⎝⎛r dr r du (3.3.3)内能是晶体体积的函数，设开始原子相距很远，逐渐被压缩相互靠近，体积逐渐缩小，系统的相互作用势能U 逐渐下降，体积缩小到一定程度时，相互作用势能达到极小值。

这时如果再压缩系统，排斥的作用转变为主要的，相互作用势能将上升。

根据功能原理，系统温度不变时外界作功p (-dV )等于相互作用势能的增加dU ：dVdUp -= (3.3.4)在一般情况下，晶体受到的仅是大气压力p 0，由于数量级为大气压的压力对一般固体体积的影响很小，因此可以近似看作零。

由上式得：00≈=-p dVdU(3.3.5) 这个关系确定了平衡晶体的体积。

体积弹性模量的定义为：0V dV dp V B ⎪⎭⎫⎝⎛-= (3.3.6)其中p 为压力，V dV /-为相对体积变化。

利用感生电偶极子推导范德瓦尔斯相互作用势作者：杨镇旭来源：《课程教育研究》2018年第48期【摘要】范德瓦尔斯相互作用是原子间相互作用的一个重要组成部分与表现形式。

本文利用简单的感生电偶极子间的静电相互作用模型，结合量子理论对范德瓦尔斯相互作用势能函数的形式进行定量的推导。

结果表明范德瓦尔斯相互作用源自于静电相互作用的量子力学效应，势能函数随着原子间距离R以1/R6的形式幂函数衰减。

本文为人们理解范德瓦尔斯相互作用提供了一个半定量描述的视角。

【关键词】范德瓦尔斯相互作用谐振子电偶极子【中图分类号】G633.7 【文献标识码】A 【文章编号】2095-3089（2018）48-0232-02一、引言原子间以及分子间相互作用力包括范德瓦尔斯相互作用造成的吸引力、泡利不相容原理造成的斥力、固有电偶极矩间相互作用、氢键等等。

范德瓦尔斯相互作用的研究对人们了解掌握原子级别微观世界中的相互作用有着重要意义。

近些年随着对于诸如石墨烯等二维材料的研究的深入，二维材料层间范德瓦尔斯相互作用对于材料性质的影响越来越受到关注。

范德瓦尔斯相互作用势实际上可以利用原子的感生电偶极子之间的静电相互作用的模型推导得出，该模型同样适用于理解分子间相互作用力。

二、感生电偶极子模型的哈密顿量四、模型的有效性和应用上述讨论中没有考虑原子所处的状态。

从微扰论的观点来看，-A/R6的势能衰减来自于电偶极矩间相互作用的二阶微扰结果。

对于S态的基态原子，电子波函数分布呈完全的球对称，于是不需要考虑电四极矩的对能量的一阶微扰的贡献。

对于非S态的原子，原子具有不为零的轨道角动量与自旋角动量，此时原子有可能具有非零的电四极矩，如果两个相互作用的原子都具有非零的电四极矩，电四极矩之间的相互作用对能量的一阶微扰的结果为1/R5的衰减形式[2]，这一项结果可能是吸引力，也可能是排斥力。

另外，全同粒子之间的交换相互作用也有可能造成能量上的变化。

不过所有的这些未在模型中考虑的因素，在对基态的角动量分量的所有可能取值做平均后，均会为0[2]，因此上述模型中得到的范德瓦尔斯相互作用势的表达式可以比较普适地应用在原子间相互作用的描述之中。

势能概念的探讨党兴菊;张瑶;孙骏【摘要】从宏观的角度看,质点组的势能可以认为是构成质点组的所有质点的势能之和.它可以分为内势能和外势能两部分.其中内势能又称为相互作用势能,质点组内部质点间的相互作用势能仅与质点间的相对位置有关,而与惯性系和坐标系的选择无关;外势能则为保守外场(力)对质点组做功的等效处理,因惯性系和坐标系的不同而改变.由于质点组的内势能的重要性和特殊性,可以直接将其称为质点组的势能.【期刊名称】《高师理科学刊》【年(卷),期】2015(035)012【总页数】5页(P44-48)【关键词】势能;质点;质点组;保守力;相互作用势能【作者】党兴菊;张瑶;孙骏【作者单位】昭通学院物理与电子信息工程学院,云南昭通657000;昭通学院物理与电子信息工程学院,云南昭通657000;昭通学院物理与电子信息工程学院,云南昭通657000【正文语种】中文【中图分类】O313.2文献[1-2]所讨论的都是单个质点的势能.文献[3]没有明确讨论单个质点的势能，文献[4]认为：“势能是属于系统的，势能是由系统内各物体间保守力的作用而存在的.所以说，势能是属于系统的，撇开系统谈单个物体的势能是没有意义的.例如：重力势能是属于地球和物体组成的系统的.应当注意，平常叙述时，常将物体和地球系统的重力势能说成是物体的重力势能，这只是叙述上的简便而已，其实它是属于物体和地球系统的，万有引力势能和弹性势能也是如此.”由此可见，谈论单个质点的势能在理论力学课程、力学课程和普通物理课程中往往存在分歧.根据文献[1-2]，讨论单个质点即文献[4]所指物体的势能是被允许的也是有意义的.那么，在力学课程和普通物理课程中如何理解类似于文献[4]的表述，如何让学生更便于理解和接受，如何有利于学生后继课程的学习，需要作深入的探究. 根据保守力的势能增量为保守力做功的负值，假定质点P在静止状态下受到恒定的保守力F的作用，但因受到约束其位置未发生变化，则F做功为零，势能增量为0.在如此选择的参照系中，质点的势能与时间无关.在相对于P沿F方向作匀速直线运动的惯性系中，P沿F方向位移不为零，从而F 做功不为零，势能增量也就不为0.在这样的参照系中，质点的位置坐标发生了变化，质点的势能相应地也发生了变化，从而质点的势能与时间有关.可见，单个质点的势能因惯性系的不同选择而不同.类似于质点组的动量和动能的定义，可以把质点组的势能定义为质点组中每个质点由于受到保守力的作用而具有的势能之和.在质点组的势能中，特别重要的是由于质点组内部质点间相互作用的保守力而具有的势能，可以把这一部分势能称为质点组的相互作用势能或内势能，在不至于混淆的情形下亦可直接称为质点组的势能.考虑仅由2个质点构成的质点组：设2个质点P与Q构成质点组，它们之间的作用力F和反作用力-F为保守力.在力F作用下，P发生元位移drP；在力-F作用下，Q发生元位移drQ，F对P所做元功为F.drP，-F对Q所做元功为-F.drQ，这2个元功也就是P和Q因F或-F具有的势能在元位移中的元增量.其和为即为该质点组的相互作用势能的增量.文献[3]指出：在很多场合下不再把外力作功dA外作进一步的分解.不过，在有保守力场的情况下，还是经常把外力作功分解为保守外力作的功和非保守外力做的功两部分.所谓“外场”，是指产生这种力场的外部物体非常庞大，内部质点的反作用力对其运动状态的影响可以忽略.如果外场是保守的，则它对系统内部质点i所做的功可写成势能减少的形式：为系统内各质点的外势能总和，即总外势能.可见，文献[3]所谓外势能即为质点组的势能与内势能（相互作用势能）之差，其增量等于质点组外部保守力对质点组内质点所做总功的相反数.上述结论可以推广到任意多个质点构成的质点组.单个质点的势能是否改变，取决于该质点是否在保守力的方向发生位移，而质点组的相互作用势能是否发生改变，则仅取决于在保守力的方向质点是否发生相对位移.在非相对论情形，质点间的相对位移与惯性系的选择无关，从而质点组的相互作用势能也与惯性系的选择无关.这正是质点组的相互作用势能重要性的体现.3.1 万有引力势能设远离其他物体的两质点mA，mB在万有引力作用下相对运动.由于万有引力是有心力，两质点的运动为平面运动.由于两物体都受力作用，因此无论是相对于mA静止还是相对于mB静止的参照系都不是惯性系.但由于两质点远离其他物体，因此两质点的质心系为惯性参照系.在经典力学中，任一时刻两质点的质心位置是唯一确定的.建立坐标系最简单的做法就是选两质点的质心为原点O，选运动平面上的任意射线为极轴建立极坐标系.设在t时刻mA的位矢为rA，位置坐标为（rA，Aθ）；mB的位矢为rB，位置坐标为（rB，Bθ）.由于O为质心，rA，rB并不相互独立，而有如下关系：.两质点的距离选无穷远点为势能零点，由万有引力产生的mA的势能为正是文献[1-4]给出的万有引力势能，亦即质点组的引力相互作用势能.由此可见，万有引力势能确实为构成质点系的两个质点的引力势能之和，其中R为相互施与引力作用的两质点间的距离，与坐标系的选择无关，也和惯性参照系的选择无关.然而，如果在由n+1个质点构成的质点组中，有一个质点的质量m0相对很大而其他质点的质量mi都很小，则尽管所有质点都受到引力作用，但m0所获得的加速度很小而其余质点的加速度则较大，例如：诸行星绕太阳的运动.这时可以忽略m0的加速度，近似把它看做惯性系的参照物，并选它作为原点建立坐标系.这样一来，就可以把m0排除在质点组之外，万有引力势能就不再是由剩下n个质点构成的质点组的相互作用势能，而成为该质点组的外势能，Ri的物理意义相应演变成了质点mi在坐标系中的矢径.而质点组内诸质点间的引力则往往可以忽略，从而引力相互势能也相应可以忽略.这正是解决位于地球表面的物体的力学问题通常所采用的近似方法.3.2 重力势能设质点m受地球重力G作用，由牛顿第三定律，地球也受到质点m的-G的力作用.G和-G互为作用力与反作用力.选取空间中任意点为原点，竖直向上方向为y轴建立坐标系，y轴正向单位矢量为j.由于地球质量远大于质点质量，因而地球因重力而产生的加速度远小于质点的重力加速度，从而可近似把地面参考系视为惯性系.在相对于地面静止的参照系看来，地球不动，-G做功为0，地球的重力势能增量为0；m从坐标为yj处掉落地面，设地面坐标为y0j，G做功为若取地面为重力势能零点，则m在掉落前的重力势能为mg（ y-y0）.自然也可以选取坐标原点处的重力势能为0，则m在空间中同一位置的势能将随着坐标原点的不同而不同.在相对地面沿竖直方向以速度vj作匀速直线运动的参照系来看，在m自高度为y 处从静止掉落地面的过程中，地球沿-G方向移动了取地面与质点m相对距离为0的点为重力势能零点，则m在高度为y处的重力势能为.可见，即便选定了重力势能零点，在不同参照系中，质点和地球的重力势能也并非保持不变；但它们的和即由质点和地球共同构成的质点组的重力势能mgh=mg（ y-y0）则为定值.需要注意的是，作为由质点与地球构成的质点组的相互作用势能（或称内势能）中的h 是指质点与“地面”的竖直距离，这里的“地面”可以是某个山巅、某个海平面，也可以是某个屋顶或某个桌面；而当mgh表示不包括地球的单个质点的重力势能（所谓外势能）时，其中的h则是指质点沿竖直向上方向坐标轴的坐标，显然这一坐标轴上的原点是可以任意选择的.对于地面上由多个质点组成的质点组，在进行力学分析中仍然是把地球本身排除在质点组之外较为简洁，这时质点组的重力势能就成为质点组因重力而产生的外势能.式中hi相应演变成为质点mi在竖直向上方向的坐标轴上的坐标.3.3 弹性势能设质点m系于劲度系数为k的理想弹簧的一端，弹簧的另一端系在固定的质点m′上，选取质点m′所在位置为原点O，沿弹簧的伸长方向为x轴建立坐标系，x轴正向单位矢量为i.则当m从位置A移动到B时，弹力F做的功为式中：x0为m在A点时弹簧的伸长量.若选质点x在A点时弹性势能为0，则质点在任意位置的弹性势能尽管弹簧的各部分在弹力的作用下会发生位移，但因为所考虑的弹簧为理想弹簧，即弹簧的质量为0，因此不能把弹簧的各部分视为质点，而只能把弹簧视为其两端所系质点受力作用的中介.在这种情形下，把固定的m′和运动的m视为一个质点组显然是不必要的.为了使讨论更为清晰起见，设想m′并非固定，而仅与m用理想弹簧相连.可以把由m′和m构成的质点组看作双原子分子的一个经典模型.在弹性力的作用下，和万有引力势能中的讨论类似，应该选择质点组的质心为坐标原点，选过两质点的直线为x轴建立坐标系，并且不失一般性，选取x轴的正向为自m′指向m的方向.于是在振动中m的坐标始终为正值而m′的坐标始终为负值.正是两质点组的弹性势能.此势能只取决于弹簧的劲度系数和弹簧所联系两质点的相对距离的变化，而与两质点的位置坐标无直接关系.然而，在m′固定并且有其他质点一并需要考虑的情形，并无必要把m′纳入质点组，此时弹性势能成为不含m′的质点组的外势能，其中x也相应演变成与m′由弹簧相连的质点沿弹簧伸缩方向偏离平衡位置的坐标.综上所述，讨论单个质点的势能是有意义的，并且质点组的势能即为所有质点势能之和.那么，为什么通常所指的质点组的势能往往是指质点组的相互作用势能即内势能呢？原因之一就是质点组的内势能只取决于质点组内部质点间的相对位置，从而与惯性系和坐标系的选择无关.另一个重要原因就是如文献[3]所指出：“从宏观的角度看，物体系有保守系和非保守系之分，前者机械能守恒，后者则不然.从微观的角度看无所谓耗散力，在一切系统中，粒子与粒子之间的相互作用可通过相互作用势来表达.”“时间均匀性，或者说，时间平移不变性意味着粒子间的相互作用势只与两粒子的相对位置有关，亦即，对于同样的相对位置，粒子间的相互作用势不应随时间而变.在这种情况下系统的总能量（动能+势能）自然是守恒的.”可见，从微观的角度看，所有的相互作用都是保守的，从而质点组的势能中只有内势能才具有决定性的意义.从宏观的角度看，质点组的势能可以认为是构成质点组的所有质点的势能之和.它可以分为内势能和外势能两部分.其中内势能又称为相互作用势能，其大小仅与质点间的相对位置有关，与惯性系和坐标系的选择无关；而外势能为保守外场做功的等效处理，因惯性系和坐标系的不同而改变.由于质点组的内势能的重要性和特殊性，在不会引起混淆的情形可以直接将其称为质点组的势能.【相关文献】[1]梁绍荣，刘昌年，正华.普通物理学（第一分册）·力学[M].3版.北京：高等教育出版社，2005[2]周衍柏.理论力学教程[M].3版.北京：高等教育出版社，2009[3]赵凯华，罗蔚茵.新概念物理教程·力学[M].北京：高等教育出版社，1995[4]马文蔚，周雨青.物理学教程（上册）[M].2版.北京：高等教育出版社，2006。