K2.07-初值定理和终值定理

拉普拉斯变换的基本定理
证明：根据拉氏变换的定义，有
L[ df (t)] df (t)estdt estdf (t)
dt
0 dt
0
est
f (t)
0
s
0
f (t)estdt
sF (s) f (0)
L[ d 2 f (t)] L[ f (t)] L{[ f (t)]} dt 2 sL[ f (t)] f (0) s[sF (s) f (0)] f (0) s2F (s) sf (0) f (0)
0
拉普拉斯变换的基本定理
7.终值定理 如果函数 f (t) 的拉氏变换为 F(s) ，且以下极限值均存在，则有
lim f (t) lim sF(s)
t
s0
证明：根据拉普拉斯变换的微分定理，可知下式成立
L[df (t)] df (t) estdt sF(s) f (0) dt 0 dt
解：三角波可表达为：
f (t) 5t 5(t 2) 101(t 2)
利用实数域的平移定理，对上式求拉氏变换，得：
F(s)
5 s2
5 s2
e2s
10 s
e2s
拉普拉斯变换的基本定理
3.复数域的平移定理
如果函数 f (t) 的拉氏变换为 F(s) ，则对任一常数 a ，有
L[eat f (t)] F (s a)
s2
s 1 ，求
2s 1
f
() 。
解：根据终值定理，可求得
解：
f () lim sF(s) lim
s 1
1
s0
s0 s2 2s 1
小结
1.微分定理 2.平移定理 3.初值定理 4.终值定理

文章标题：深度探析拉普拉斯变换初值定理和终值定理目录：1. 引言2. 拉普拉斯变换初值定理2.1 定义和原理解析2.2 详细推导与举例说明2.3 个人观点与理解3. 拉普拉斯变换终值定理3.1 概念解析3.2 推导及应用范围3.3 个人见解和扩展思考4. 总结与回顾1. 引言拉普拉斯变换初值定理和终值定理是微积分中的重要概念，它们在信号处理、控制理论、电路分析等领域有着广泛的应用。

通过深入探究这两个定理，不仅可以帮助我们加深对拉普拉斯变换的理解，还能为日后的应用打下坚实的基础。

2. 拉普拉斯变换初值定理2.1 定义和原理解析拉普拉斯变换初值定理是指如果函数f(t)在t=0处连续，并且t<0时f(t)=0，则拉普拉斯变换的初值f(0-)等于原函数的初始值f(0)。

2.2 详细推导与举例说明以实际函数为例，对拉普拉斯变换初值定理进行推导和举例说明，可以更加直观地理解这一概念的含义和应用。

2.3 个人观点与理解在我看来，拉普拉斯变换初值定理的重要性在于它可以帮助我们在进行变换计算时更加便捷准确地处理初始值的情况，同时也为我们提供了从初始值到变换结果的直观对应关系。

3. 拉普拉斯变换终值定理3.1 概念解析拉普拉斯变换终值定理是指如果函数f(t)在t=∞时有界，并且在t>0时f(t)有有限个第一类间断点，则拉普拉斯变换的终值lim(s→0)F(s)等于原函数f(t)的终值lim(t→∞)f(t)。

3.2 推导及应用范围通过数学推导和具体应用范例，可以更好地理解拉普拉斯变换终值定理在控制理论、信号处理等领域中的作用和价值。

3.3 个人见解和扩展思考我认为拉普拉斯变换终值定理不仅仅是一种数学工具，更是一种思维方式，它能够帮助我们从全局的角度去理解和分析问题，为我们解决实际问题提供了新的视角和思路。

4. 总结与回顾通过对拉普拉斯变换初值定理和终值定理的深度探讨，我们不仅对这两个定理有了更深入的理解，也为我们今后在工程技术和科学研究中的应用提供了更加丰富的思维方式。

d2 dt 2
r(t)
s2 R(s) sr(0 ) r'(0 )
(s2 3s 2)R(s) (s 5) 2(s 2) s3
R(s) 5 3 1 s 1 s 2 s 3
r(t ) (5et 3e2t e3t ) (t )
例2：LTI因果系统 H (s)
f (t) F(s)
f (at) 1 F( s ),a 0 aa
单边
f (t) F(s)
f (t t0 ) es0t F(s)
es0t f (t) F(s s0 )
f (at) 1 F( s ),a 0 aa
t f ( )d 1 F (S ) G(0 )
Rzi (s)
s2 Rzi (s) sr(0 ) r'(0 )
(s2 3s 2)Rzi (s) s 5
Rzi (s)
(s2
s5 3s 2)
4 3 s1 s2
rzi (t ) (4et 3e2t ) (t )
例1：
已
知
一
线
性
系
统d 2 dt 2

H(
j)
j s

bm sm bm1sm1 b0 sn an1sn1 a0
h(t) H(s)
例1： 已 知 一 线 性 系 统
d2 dt 2
r(t)

3
d dt
r(t)

2r (t )

d dt
e(t )

2e(t )
若r(0 ) 1; r '(0 ) 2;e(t ) 2e 3t (t ),

所以
t 0
lim f (t ) f (0 ) lim sF ( s)
例：已知
求
f1 (t ) f2 (t )
的拉普拉斯变换
F( s)
解：F(s) F1 (s) F2 (s)
1 1 s 1 1 s 1 (s 1)(s 2) (s 1)(s 2) s 2
说明：前面求正余弦信号的拉普拉斯变换时已经用到了线性性。
二．延时（时域平移）
证明：
L f (t )e
α t
α t st f ( t )e e d t F (s α) 0

例：求 e α t cos ω0t 的拉氏变换
解：已知 : L cos(ω0t )u (t )
t
sα 所以 e cos(ω0t )u (t ) 2 ( s α ) 2 ω0 ω0 t 同理 : e sin(ω0t )u (t ) 2 ( s α ) 2 ω0
所以
1 1 F ( s) F1 ( s ) 2 (1 e2 s )2 s 2s
七．s 域微分定理
若
L f (t ) F (s ) d F ( s) L tf (t ) ds n d F ( s) n L (t ) f (t ) d sn
则
n 取正整数
(2)信号一定是右移 (3)表达式
所表示的信号不能用时移性质
二．延时（时域平移）
例：已知
1 f (t ) 0
0<t <t0
其余
求
F( s)
解： 因为
所以
f (t ) u (t ) u (t t 0 )

初值定理和终值定理常用于由F(s)直接求f(0+)和f(∞), 而不必求出原函数f(t)。 初值定理
设函数f(t)不含(t)及其各阶导数（即F(s)为真分式，
若F(s)为假分式化为真分式），
则 f (0) lim f (t) lim sF(s)
t 0
s
终值定理
若f(t)当t →∞时存在，并且 f(t) ← → F(s) , Re[s]>0,
F(s)
1
s2
2s 2 2s
2
1
F1(s)
f
(0)
lim
s
sF1(s)
lim
s
2s2 2s s2 2s 2
2
f
()
lim
s0
sF
(s)
lim
s0
s2
s3 2s
2
0
0<0，则
f () lim sF(s) s0
拉普拉斯变换的性质—初值、终值定理
例1
F(s)
s2
2s 2s
2
f (0) lim sF(s) lim 2s2 2
s
s s 2 2s 2
f () lim sF(s) lim 2s2 0
s0
s0 s 2 2s 2
例2

F(s)
s2
s2 2s 2
拉普拉斯变换的性质—初值、终值定理
知识点K1.10
拉普拉斯变换的性质—初值、终值定理
主要内容： 1.拉普拉斯变换的初值定理 2.拉普拉斯变换的终值定理 基本要求： 1.掌握拉普拉斯变换的初值、终值定理 2.熟练计算初始值和终止值
拉普拉斯变换的性质—初值、终值定理
K1.10 拉普拉斯变换的性质—初值、终值定理

z1 z
z 1
注意：收敛域要求含单位圆。
ቤተ መጻሕፍቲ ባይዱ
4
Xidian University, ICIE. All Rights Reserved
1、初值定理： 如果序列在k<M时，f(k)=0， f(k)←→F(z) ，<|z|<∞ 则序列的初值
f (M ) lim zmF (z) z
对因果序列f(k)， f (0) lim F (z) z
2
Xidian University, ICIE. All Rights Reserved
初值定理和终值定理
证明：


F (z) f (k)zk f (k)zk
k
kM
f (M )zM f (M 1)z(M 1) f (M 2)z(M 2) ...
两边乘zM，得
zM F z f (M ) f (M 1)z1 f (M 2)z2 ...
上式取z→∞，得
f (M ) lim zM F (z) z
3
Xidian University, ICIE. All Rights Reserved
初值定理和终值定理 2、终值定理： 如果序列存在终值，即：
则序列的终值
f () lim f (k) k
f () lim z 1 F (z) lim(z 1)F (z)
知识点K2.07
初值定理和终值定理
初值定理和终值定理
主要内容：
初值定理和终值定理
基本要求：
熟练运用初值定理和终值定理
1
Xidian University, ICIE. All Rights Reserved

函数 u(t t0) 在间断点 t t0 上的导数。
(tt0)ddtu(tt0) 相反，如果对单位脉冲函数(t t0)积分，积分的 结果就是单位阶跃函数u(t t0)
利用脉冲函数的tt0概(t念t，0)d我t们u(t可t以0)对包含不连续
点的函数进行微分，从而得到一些脉冲，这些
脉冲的量值等于每一个相应的不连续点上的量
1 s3
发生在t＝t0时的单位加速度函数通常写成 a(t t0)
a(t)
a(t t0)
8 6 4 2
12 34
0
(a)
t
0
t 0 (b)
t
2. 关于拉氏积分下限的说明 在某些情况下，如果时间函数f (t)在t＝0处有
脉冲函数 (t) ，必须明确地指出拉氏积分的下限 是0－还是0＋。
L[f(t)]0 f(t)esd t t L[f(t)]0 f(t)esd t t00f(t)esd t tL[f(t)]
d2 Ldt2
f(t)s2F(s)s(f0)f(0)
f (0)是df (t)/dt在t＝0时的值
证明：Ld2dft2(t)
est
df (t) dt
0
s
0
df (t) dt
estdt
f (0)s[sF(s) f (0)]
s2F(s)sf(0) f (0)
导出时间函数 f (t)的n阶导数微分性质
(2) 当求解控制系统输入输出微分方程时，求解 的过程得到简化，可以同时获得控制系统的瞬态 分量和稳态分量。
(3) 拉氏变换可把时域中的两个函数的卷积运算 转换为复频域中两函数的乘法运算。
2.1 拉氏变换的概念
2.1.1问题的提出
单位阶 跃函数

拉普拉斯变换的初值定理和终值定理的作用下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!拉普拉斯变换的初值定理和终值定理的作用引言拉普拉斯变换是一种重要的数学工具，在工程、物理、控制论等领域有着广泛的应用。

拉普拉斯变换的性质—初值、终值定理
知识点K1.10
拉普拉斯变换的性质—初值、终值定理
主要内容： 1.拉普拉斯变换的初值定理 2.拉普拉斯变换的终值定理 基本要求： 1.掌握拉普拉斯变换的初值、终值定理 2.熟练计算初始值和终止值
1
拉普拉斯变换的性质—初值、终值定理
ቤተ መጻሕፍቲ ባይዱ
K1.10 拉普拉斯变换的性质—初值、终值定理
初值定理和终值定理常用于由F(s)直接求f(0+)和f(∞), 而不必求出原函数f(t)。 初值定理
设函数f(t)不含(t)及其各阶导数（即F(s)为真分式，
若F(s)为假分式化为真分式），
则 f (0) lim f (t) lim sF(s)
t 0
s
终值定理
若f(t)当t →∞时存在，并且 f(t) ← → F(s) , Re[s]>0,
0<0，则
f () lim sF(s) s0
2
拉普拉斯变换的性质—初值、终值定理
例1
F(s)
s2
2s 2s
2
f (0) lim sF(s) lim 2s2 2
s
s s 2 2s 2
f () lim sF(s) lim 2s2 0
s0
s0 s 2 2s 2
例2
s2 F(s)
s2 2s 2
F(s)
1
2s 2 s2 2s
2
1
F1(s)
f
(0)
lim
s
sF1(s)
lim
s
2s2 2s s2 2s 2
2
f () lim sF(s) lim s3 0
s0
s0 s2 2s 2
3

F(s) 称为象函数（transform function），属复频域 （complex frequency domain） 。象函数F(s) 用大写字母 表示 ，如 I(s)，U(s)。
记号 ℒ [f(t)]表示取拉氏变换。
ℒ -1 [F(s)]表示取拉氏反变换。
机械工程控制基础
拉普拉斯变换及反变换
lim f (t)存在时 ，则
t
f () lim f (t) lim sF(s)
t
s0
机械工程控制基础
拉普拉斯变换及反变换
例1
1
u(t)
t 0
lim s
s
s
1
例2 I(s) 5 2 s1 s2
i(0 ) lim s( 5 2 ) lim( 5 2 ) 3 s s 1 s 2 s 1 1/ s 1 2 / s
机械工程控制基础 二、拉氏变换的优点
应用拉氏变换：
拉普拉斯变换及反变换
• （1）求解方程得到简化。 拉氏变换将“微分”变换成“乘法”，“积分”
变换成“除法”。即将微分方程变成代数方程。
• （2）初始条件自动包含在 变换式里。
机械工程控制基础 拉氏变换已考虑了初始条件
拉普拉斯变换及反变换
LT f (t) F(s)
t
f ( ) d
0
s L
t
0
f
( ) d
t 0
f
( )d积 分上限也应为0-
t 0
S L
t 0
f
(
)
d
∴
L
t
f
0
( ) d
1 s
L
f
(t )
例
机械工程控制基础

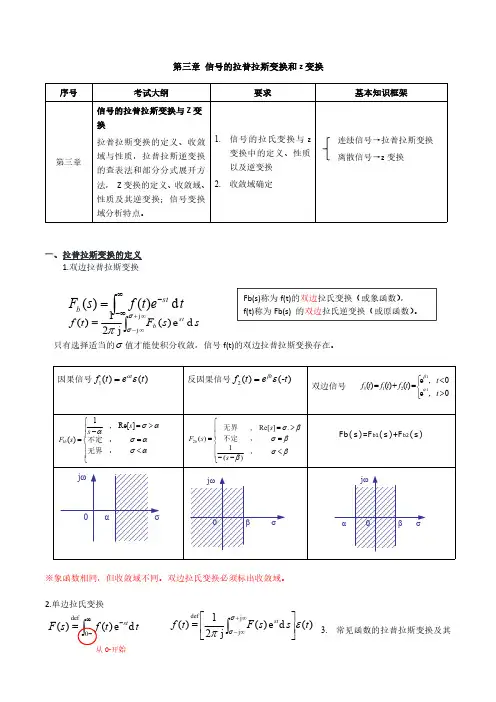
⎰∞∞--=t e t f s F st b d )()(⎰∞--=0def d e )()(t t f s F st)(d e )(j 21)(j j deft s s F t f st επσσ⎥⎦⎤⎢⎣⎡=⎰∞+∞-第三章信号的拉普拉斯变换和z 变换一、拉普拉斯变换的定义1.双边拉普拉斯变换只有选择适当的σ值才能使积分收敛，信号f(t)的双边拉普拉斯变换存在。

※象函数相同，但收敛域不同。

双边拉氏变换必须标出收敛域。

2.单边拉氏变换3.常见函数的拉普拉斯变换及其⎰∞+∞-=j j d e )(j21)(σσπs s F t f st b Fb(s)称为f(t)的双边拉氏变换（或象函数），f(t)称为Fb(s)的双边拉氏逆变换（或原函数）。

从0-开始收敛域二、拉普拉斯变换性质线性性质尺度变换证明：[]⎰∞--=de)()(tatfatf L st，则令atτ=时移特性与尺度变换相结合复频移（s域平移）特性时域的微分特性（微分定理）若f(t)←→F(s),Re[s]>σ0,则f’(t)←→sF(s)–f(0-)证明：()()()())(deedessFfttsft ftt f ststst+-=⎥⎦⎤⎢⎣⎡--='--∞-∞---∞-⎰⎰推广：()()[])0()0()()0(d)(d22----'--='--=⎥⎦⎤⎢⎣⎡fsfsFsffsF sttfL∑-=----=⎥⎦⎤⎢⎣⎡1)(1)0()(d)(d nrrrnnnfssFsttfL若f1(t)←→F1(s)Re[s]>σ1,f2(t)←→F2(s)Re[s]>σ2则a1f1(t)+a2f2(t)←→a1F1(s)+a2F2(s)Re[s]>max(σ1,σ2)若f(t)←→F(s),Re[s]>σ0，且有实数a>0，则f(at)←→)(1asFa若f(t)<----->F(s),Re[s]>σ0,且有实常数t0>0,则f(t-t0)ε(t-t0)<----->e-st0F(s),Re[s]>σ0若f(t)←→F(s),Re[s]>σ0,且有复常数s a=σa+jΩa,则f(t)e s a t←→F(s-s a),Re[s]>σ0+σas-→2：?)(sin ←→t t t ε=三、拉普拉斯逆变换三种方法：（1）查表（2）利用性质（3）部分分式展开-----结合∴......,,321为不同的实数根，n p p p p nn p s K p s K p s K s F -++-+-= 2211)(ip s i i s F p s K =-=)()()(e ]1[1t p s L t p i i ε=--若象函数F(s)是s 的有理分式，可写为1110111.......)(a s a s a s b s b s b s b s F n n n m m m m ++++++++=----若m ≥n （假分式）,可用多项式除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和。

简写 F(s) =
s为复频率
[ f (t)]
复频域函数F(s)(象函数) F(s)(象函数 复频域函数F(s)(象函数)
s = σ + jω
1.复数与复平面 1.复数与复平面
的数， 形如 a + bi ( a , b ∈ R ) 的数，叫做复数
C = {z | z = a + bi, 其中a, b ∈ R )
dn f (t ) [ ]= SnF(S) − Sn−1 f (0− ) −L− f n−1(0− ) dtn
3）.积分性质
设： [ f (t )] = F(s)
： 则 [∫0
t
−
证：令
[∫0 f (t )dt ] = φ(s)
−
−
t
1 f (t)dt] = F(s) s
应用微分性质
d t [ f (t )] = ∫0 f (t)dt dt t F(s) = sφ(s) − ∫0 f (t)dt t=0
[ f2( t )] = F ( S ) 2
= A1F ( S ) + A2F2 ( S ) 1
= ∫0 [A1 f1( t ) + A2 f2( t )]e−stdt 证： A1 f1( t ) + A2 f2 ( t )
∞
[
]
= ∫0 A1 f1( t )e dt + ∫0 A2 f2( t )e dt
t ≥0 t <0
u(t)-----单位阶跃函数
斜坡信号为匀速信号，适于测试匀速系统。
抛物线信号（ 抛物线信号（Parabolic Function） ）
0.5R∗t 2 r(t) = 0.5R∗t ∗u(t) = 0

稳定性分析方法
利用拉普拉斯变换，通过计算系统的极点和零点，判 断系统的稳定性。
电路系统的频率响应分析
频率响应定义
电路系统在不同频率下的输入与输出关系称为频率响应。
频率响应分析方法
通过拉普拉斯变换将时域函数转换为复频域函数，进而分析频率 响应。
频率响应特性
频率响应具有幅度和相位特性，这些特性决定了电路系统在不同 频率下的性能表现。
到该函数的拉普拉斯变换。
拉普拉斯变换具有线性性和时移性等性质，使得复杂电路的分
03
析变得简单。
拉普拉斯变换的性质
1 2 3
线性性
如果函数$f(t)$和$g(t)$的拉普拉斯变换分别为 $F(s)$和$G(s)$，那么对于任意实数$k$和$l$， 有$(kf(t)+lg(t))的拉普拉斯变换=kF(s)+lG(s)$。
04
拉普拉斯变换的逆变换
逆变换的定义和性质
逆变换的定义
如果一个函数f(t)的拉普拉斯变换存在，那么就存在另一个函数g(s)的拉普拉斯 变换等于f(t)，并且g(s)可以通过一定的积分运算从f(t)得到，这个过程就是逆 变换。
逆变换的性质
逆变换具有线性、时移、频移、微分、积分等性质，这些性质在求解逆变换时 非常有用。
时移性
如果函数$f(t)$的拉普拉斯变换为$F(s)$，那么 对于任意实数$a$，有$(f(t-a))的拉普拉斯变换 =e^{-as}F(s)$。
频移性
如果函数$f(t)$的拉普拉斯变换为$F(s)$，那么 对于任意实数$b$，有$(f(t)e^{bt})的拉普拉斯 变换=F(s-b)$。
拉普拉斯变换的应用
拉普拉斯变换的微分性质
微分性质
如果函数f(t)的拉普拉斯变换存在，那么对于实数a，函数f''(t)的拉普拉斯变换等于函数f(t)的拉普拉斯变换乘以 s^2。

机械工程控制基础
• 作业
1、 写出拉普拉斯变换定义式 2、
拉普拉斯变换及反变换
机械工程控制基础
拉普拉斯变换及反变换
1
__
(s-1)2
机械工程控制基础
拉普拉斯变换及反变换
机械工程控制基础
s s
1 s 1 sa
由终值定理得
f () lim sF ( s) lim
s 0 s 0
1 s 0 sa
机械工程控制基础
七、时域卷积性 ： 8时域卷积性
L 若f1 (t ) F1 ( s ), f 2 (t ) F2 ( s ) L 则f1 (t ) f 2 (t ) F1 ( s ) F2 ( s )
机械工程控制基础
(1)
利用
拉普拉斯变换及反变换
ℒ
机械工程控制基础
拉普拉斯变换及反变换
机械工程控制基础
拉普拉斯变换及反变换
机械工程控制基础
拉普拉斯变换及反变换
机械工程控制基础
拉普拉斯变换及反变换
机械工程控制基础
拉普拉斯变换及反变换
机械工程控制基础
拉普拉斯变换及反变换
机械工程控制基础
拉普拉斯变换及反变换
n [ t ] ℒ [ t n 1 ] s
n
机械工程控制基础
拉普拉斯变换及反变换
n ℒ [ t ] ℒ [ t n 1 ] s
n
1 当n＝1， ℒ [t ] 2 ； s 2 2 当n＝2，ℒ [t ] 3 ； s
依次类推， 得 ℒ
机械工程控制基础
常 用 函 数 的 拉 普 拉 斯 变 换 表 δ(t) δn(t) u(t) t tn e-at te-at tne-at e-jwt 1 sn 1/s 1/s2

z 2 X z x 2 z 1 x 1 X
11
第
证明左移位性质 页
根据单边z变换的定义，可得
Zxkm k xkm zk k0
zm xkmzkm k0
令 nkmzm xnzn nm
zmxnznm 1xnzn
n0
n0
zmXzm n01xnzn
X
12
第
(2)右移位性质 页
xkm ,xkm 只是位置 xk的 变长 化度 ，
X
9
第
(1)左移位性质
页
若 x (k )(k ) X (z) z
则 x ( k m )( k ) z m X (z ) m 1 x ( k )z k z
k 0
其中m为正整数
x k 1 ( k ) z z X z 0 x
11页页线性性质移序性质序列乘k性质序列线性加权z域尺度变换性质序列指数加权初值定理终值定理时域卷积定理z域卷积定理自学反映离散信号在时域特性和z域特性之间的关系以上性质无特别说明既适用于单边也适用于双边
1
第二节 Z变换的性质
第 页
反映离散信号在时域特性和z域特性之间的关系 线性性质 移序性质 序列乘K性质（序列线性加权） Z域尺度变换性质（序列指数加权） 时域卷积定理
z域卷积定理（自学）
初值定理
以上性质无特别说明既适用于单边也适用于双边.
X
2
一．线性 (叠加性和齐次性）
第
页
若Zx1(k)X1(z)
zRx1
Zx2(k)X2(z)
zRx2
则Za1x (k)b2x(k)a1 X (z)bX 2(z)
a,b为任意常数。
ROC：一般情况下，取二者的重叠部分

解：F (s) [ (t) 6 e2tu(t) 6 e3tu(t)]estdt
5
5
(t)estdt 6 e2tu(t)estdt 6 e3tu(t)estdt
5
5
F(s) 1 6[
1
1 ]
s2 s 12 ,
2 3
5 s 2 s 3 (s 2)(s 3)
？
则：
f
(at) L
1 a
F ( s ), a
ROC : Rc aR
？
信号 系统 响应
例：设信号f(t)的拉氏变换为F(s)，收敛域:σ>σ0。 求信号 e3t f (2t 1) 的拉氏变换，并标明收敛域。
解： f (t 1) L esF(s), ROC : 0
尺度变换特性
f (2t 1) L 1 es/2F(s / 2), 2
j
区域Ⅰ 区域Ⅱ
s平面
区域 Ⅲ
3
2
？
信号 系统 响应
(1)若收敛域ROC为为区域Ⅰ，即σ <-3，则 f (t) e3tu(t) e2tu(t)
(2)若收敛域ROC为为区域Ⅲ，即σ>2 ，则
f (t) e3tu(t) e2tu(t)
(3)若收敛域ROC为为区域Ⅱ，即-3<σ<2 ，则
f (t) e3tu(t) e2tu(t)
ROC : 20
s域移位特性
e3t f (2t 1) L 1 e(s3)/2F[(s 3) / 2], 2
ROC : 20 3
5.共轭特性
？
信号 系统 响应
若: f (t)L F(s), ROC: R
则: f (t) L F(s), ROC : Rc R

初值定理和终值定理 2、终值定理： 如果序列存在终值，即：
则序列的终值
f () lim f (k) k
f () lim z 1 F (z) lim(z 1)F (z)
z1 z
z 1
注意：收敛域要求含单位圆。
4
时 f(k)=0 的 序 列 。 由 象 函 数 直 接 求 序 列 的 初 值 f(M), f(M+1), … 而不必求得原序列。
1、初值定理： 如果序列在k<M时，f(k)=0， f(k)←→F(z) ，<|z|<∞ 则序列的初值
f (M ) lim zmF (z) z
对因果序列f(k)， f (0) lim F (z) z
初值定理和终值定理
证明：

F (z) f (k)zk f (k)zk
k
kM
f (M )zM f (M 1)z(M 1) f (M 2)z(M 2) ...
两边乘zM，得
zM F z f (M ) f (M 1)z1 f (M 2)z2 ...
上式取z→∞，得
f (M ) lim zM F (z) z 3
熟练运用初值定理和终值定理初值定理和终值定理k207初值定理和终值定理初值定理适用于右边序列即适用于kmm为整数时时fk0的序列
知识点K2.07
初值定理和终值定理
初值定理和终值定理
主要内容：
初值定理和终值定理
基本要求：
熟练运用初值定理和终值定理
1
初值定理和终值定理
K2.07 初值定理和终值定理 初值定理适用于右边序列，即适用于k<M(M为整数)