电学中的变化量

电学变化量问题，难度较大且易错，本文拟结合典型例题进行分类解析说明，希望能对大家有所裨益。

一、同类物理量变化量大小的比较类此类问题是在“当电路状态发生变化时，判定电路各部分电流、电压如何变化”类题目的基础上，进一步发展而来。

因此，处理此类问题时，要首先定性地判定电流、电压如何变化，然后再进行同类物理量变化量大小的比较。

例1 如图1所示电路，电源电压保持不变，当滑动变阻器的滑片P由置于某一位置，向右移动到另一位置时，R1、R2两端的电压变化量分别为△U1和△U2（均取为绝对值），则A．△U1＜△U2B．△U1＞△U2C．△U1＝△U2D．无法判断△U1、△U2哪个大分析与解：当滑动变阻器的滑片P向右移动时，变阻器接入电路的阻值是变大的，根据串联电路电阻的特点，可知电路中的总电阻将变大，又由欧姆定律可知，电路中的电流将变小，定值电阻R0、R2两端的电压也均是变小的。

因电源电压保持不变，其值总等于定值电阻R0、R2两端的电压与变阻器两端的电压之和，既然定值电阻R0、R2两端的电压均变小，所以变阻器两端的电压必是变大的，且定值电阻R0、R2两端的电压减小量之和应与变阻器两端电压的增大量相等，即△U0+△U2=△U1。

于是可知，△U1＞△U2，应选B。

本题中，若定值电阻R0＞R2，则定值电阻R0、R2两端的电压变化量谁大谁小呢？设滑片“置于某一位置”时，电路中的电流为I；滑片向右移动到“另一位置”时，电路中的电流为I‘，则R0、R2两端的电压变化量分别为△U0=（I—I‘）R0，△U2=（I—I‘）R2，即△U0∶△U2=R0∶R2。

因为R0＞R2，所以有△U0＞△U2。

读者不妨自己思考：若滑动变阻器的滑动触片是向左移动的，△U0、△U1、△U2的关系又将怎样？（答案：△U1＞△U0＞△U2）例2如图2所示电路中，电源电压保持不变，闭合开关S，当滑动变阻器R1的滑动触片向左移动时，电流表A和A1的读数都将发生变化。

电学变化量问题知识点一：两个电阻组成的串联电路(一) 电压变化量之间的关系➢当滑片向右滑动时，R 2增大，R 总增大，I 减小，电压表V 1的示数减小，电压表V 2的示数增加。

➢因为电源电压保持不变，所以电压表V 1示数的减少量等于电压表V 2示数的增加量，即21U U ∆=∆(二) 变化量之间的比值(三) 结论： ➢电源电压保持不变，所以21U U ∆=∆；➢ 定值电阻两端的电压变化量与电流变化量的比值不变，比值为此定值电阻，即IU R ∆∆=11 ➢滑动变阻器两端的电压变化量和电流变化量之比等于除滑变之外其他定值电阻，即IU R ∆∆=21知识点二：三个电阻组成的串联电路(一) 电压变化量之间的关系➢ 电源电压保持不变U U U U =++321 312U U U ∆+∆=∆∴，➢ 在R 1、R 2两端并联一个电压表V 4，UU U =+3434U U ∆=∆∴；➢ 在R 2、R 3两端并联一个电压表V 5，U U U =+51 15U U ∆=∆∴(二) 变化量之间的比值(三) 结论：➢ 电表示数之比的变化情况由电压表所测的电阻决定，如果测的是定值电阻，则示数之比不变；如果测的是滑动变阻器，则示数之比的变化情况与电阻的变化相同。

➢ 变化量之比均为定值电阻，所以变化量之比都不变。

定值电阻两端的电压变化量和电流变化量之比等于其定值电阻，滑动变阻器两端的电压变化量和电流变化量之比等于除滑变之外其他定值电阻（之和）。

(四) 变化量大小比较 已知321R R R >>，则321,,U U U ∆∆∆的大小关系为：312U U U ∆>∆>∆(五) 比例计算312131U U U U R R ∆∆== 知识点三：电功率变化量(一)定值电阻电功率的变化量②……………①……………12111211R I P R I P '='=1211111111111212112112111R I UI U U I R I R I I R I I I I R I I R I R I P P P ⋅∆>∆⋅∆>⎪⎭⎫ ⎝⎛+'⋅∆=⎪⎭⎫ ⎝⎛+'⋅∆=⋅⎪⎭⎫ ⎝⎛+'⎪⎭⎫ ⎝⎛-'=⋅⎪⎪⎭⎫ ⎝⎛-'=-'=-'=∆同理：1211R U I I U P ∆>⎪⎭⎫ ⎝⎛+'⋅∆=∆(二) 总功率的变化量I U P ∆⋅=∆【题型分类】1.同类变化量大小比较2.电表示数之比与电表变化量之比3.变化量计算4.电功率变化量【专题讲练】1. 同类变化量大小比较（2011延庆一模）11.图4是小李探究电路变化的实验电路，其中R1、R2为定值电阻，R0为滑动变阻器，R max为滑动变阻器的最大阻值。

电量与电流的关系公式电量与电流是电学中两个重要的物理量，它们之间存在着密切的关系。

在电学中，电量通常指的是电荷量，用符号Q表示，单位是库仑（C）。

而电流是单位时间内通过导体横截面的电荷量，用符号I 表示，单位是安培（A）。

根据电学的基本原理，电流的大小与电荷量的变化有着直接的关系。

当单位时间内通过导体横截面的电荷量增加时，电流的大小也会增加；反之，当单位时间内通过导体横截面的电荷量减少时，电流的大小也会减小。

因此，可以得出电流与电荷量之间的关系公式如下：I = ΔQ/Δt式中，I表示电流，ΔQ表示单位时间内通过导体横截面的电荷量的变化量，Δt表示时间的变化量。

根据这个关系公式，我们可以得出以下几个结论。

当电荷量不变时，电流的大小也不变。

这是因为单位时间内通过导体横截面的电荷量不变，所以电流的大小也保持不变。

当电荷量增加时，电流的大小也会增加。

这是因为单位时间内通过导体横截面的电荷量增加，所以电流的大小也会增加。

当电荷量减少时，电流的大小也会减小。

这是因为单位时间内通过导体横截面的电荷量减少，所以电流的大小也会减小。

电量与电流之间存在着直接的关系，即电流的大小与单位时间内通过导体横截面的电荷量的变化量成正比。

这个关系公式为I = ΔQ/Δt。

根据这个公式，我们可以推导出许多电学中的重要定律和规律，如欧姆定律、基尔霍夫定律等。

电量与电流的关系公式在电学领域有着广泛的应用。

它不仅可以帮助我们理解电流的产生和传输过程，还可以用于计算电路中的各种参数。

因此，掌握电量与电流的关系公式对于学习和应用电学知识来说非常重要。

我们要注意的是，电量与电流的关系公式只是电学中的一个基础公式，它描述了电流与电荷量之间的关系。

在实际应用中，还需要结合其他电学定律和规律进行综合分析和计算。

因此，在学习和应用电学知识时，我们需要深入理解电量与电流的关系公式，并将其与其他相关知识相结合，以便更好地理解和应用电学知识。

高中物理电学公式大全电学公式在高中物理知识中所占比重较大，是高中学生学习的重点内容。

下面店铺给大家带来高中物理电学公式，希望对你有帮助。

高中物理电场公式1.两种电荷、电荷守恒定律、元电荷：(e=1.60×10-19C);带电体电荷量等于元电荷的整数倍2.库仑定律：F=kQ1Q2/r2(在真空中){F:点电荷间的作用力(N)，k:静电力常量k=9.0×109Nm2/C2，Q1、Q2:两点电荷的电量(C)，r:两点电荷间的距离(m)，方向在它们的连线上，作用力与反作用力，同种电荷互相排斥，异种电荷互相吸引｝3.电场强度：E=F/q(定义式、计算式){E：电场强度(N/C)，是矢量(电场的叠加原理)，q：检验电荷的电量(C)｝4.真空点(源)电荷形成的电场E=kQ/r2 {r：源电荷到该位置的距离(m)，Q：源电荷的电量｝5.匀强电场的场强E=UAB/d {UAB:AB两点间的电压(V)，d:AB两点在场强方向的距离(m)｝6.电场力：F=qE {F:电场力(N)，q:受到电场力的电荷的电量(C)，E:电场强度(N/C)｝7.电势与电势差：UAB=φA-φB，UAB=WAB/q=-ΔEAB/q8.电场力做功：WAB=qUAB=Eqd{WAB:带电体由A到B时电场力所做的功(J)，q:带电量(C)，UAB:电场中A、B两点间的电势差(V)(电场力做功与路径无关),E:匀强电场强度,d:两点沿场强方向的距离(m)｝9.电势能：EA=qφA {EA:带电体在A点的电势能(J)，q:电量(C)，φA:A点的电势(V)｝10.电势能的变化ΔE AB=EB-EA {带电体在电场中从A位置到B位置时电势能的差值｝11.电场力做功与电势能变化ΔEAB=-WAB=-QuAb (电势能的增量等于电场力做功的负值)12.电容C=Q/U(定义式,计算式) {C:电容(F)，Q:电量(C)，U:电压(两极板电势差)(V)｝13.平行板电容器的电容C=εS/4πkd(S:两极板正对面积，d:两极板间的垂直距离，ε：介电常数)14.带电粒子在电场中的加速(V0=0)：W=ΔEK或qU=mVt2/2，Vt=(2qU/m)1/215.带电粒子沿垂直电场方向以速度V0进入匀强电场时的偏转(不考虑重力作用的情况下)类平抛运动;垂直电场方向:匀速直线运动L=V0t，平行电场方向:初速度为零的匀加速直线运动d=at2/2，a=F/m=qE/m高中物理恒定电流公式1.电流强度：I=q/t{I:电流强度(A)，q:在时间t内通过导体横载面的电量(C)，t:时间(s)｝2.欧姆定律：I=U/R {I:导体电流强度(A)，U:导体两端电压(V)，R:导体阻值(Ω)｝3.电阻、电阻定律：R=ρL/S{ρ:电阻率(Ω?m)，L:导体的长度(m)，S:导体横截面积(m2)｝4.闭合电路欧姆定律：I=E/(r+R)或E=Ir+IR也可以是E=U内+U 外{I:电路中的总电流(A)，E:电源电动势(V)，R:外电路电阻(Ω)，r:电源内阻(Ω)｝;5.电功与电功率：W=UIt，P=UI{W:电功(J)，U:电压(V)，I:电流(A)，t:时间(s)，P:电功率(W)｝;6.焦耳定律：Q=I2Rt{Q:电热(J)，I:通过导体的电流(A)，R:导体的电阻值(Ω)，t:通电时间(s)｝;7.纯电阻电路中:由于I=U/R,W=Q，因三此W=Q=UIt=I2Rt=U2t/R;8.电源总动率、电源输出功率、电源效率：P总=IE，P出=IU，η=P出/P总{I:电路总电流(A)，E:电源电动势(V)，U:路端电压(V)，η：电源效率｝9.电路的串/并联串联电路(P、U与R成正比) 并联电路(P、I与R 成反比)电阻关系(串同并反) R串=R1+R2+R3+ 1/R并=1/R1+1/R2+1/R3+电流关系 I总=I1=I2=I3 I并=I1+I2+I3+电压关系 U总=U1+U2+U3+ U总=U1=U2=U3功率分配 P总=P1+P2+P3+ P总=P1+P2+P3+10.欧姆表测电阻：(1)电路组成 (2)测量原理两表笔短接后,调节R0使电表指针满偏，得Ig=E/(r+Rg+R0);接入被测电阻Rx后通过电表的电流为Ix=E/(r+Rg+R0+Rx)=E/(R中+Rx);由于Ix与Rx对应，因此可指示被测电阻大小(3)使用方法:机械调零、选择量程、欧姆调零、测量读数{注意挡位(倍率)｝、拨off挡。

微梯度和微电位微梯度和微电位是两个在科学研究中常用的概念，它们在不同领域有着不同的应用。

本文将分别介绍微梯度和微电位的定义、特点以及应用，并探讨它们在科学研究中的重要性。

一、微梯度微梯度指的是一个非常小的梯度，即在一个非常短的距离内，某个物理量的变化量。

在物理学、化学、生物学等领域中，微梯度常常用于描述一种物理量随空间位置的变化情况。

它可以帮助研究者更加准确地了解物质的分布规律。

在物理学中，微梯度可以用来描述电场、磁场、温度场等的变化情况。

例如，在电场中，微梯度可以用来表示电势的变化率，即单位距离内电势的变化量。

在化学反应中，微梯度可以用来描述反应速率随位置的变化情况。

在生物学中，微梯度常常用于描述细胞内各种物质的浓度分布，从而揭示细胞内的生物过程。

微梯度的研究对于科学研究具有重要意义。

首先，微梯度可以帮助研究者更加准确地描述物质的分布规律，从而揭示物质运动的机制。

其次，微梯度可以用来研究物质的传输过程，有助于优化工艺和设计新的材料。

此外，微梯度还可以用来研究生物体内的各种生理过程，对于深入理解生命现象具有重要意义。

二、微电位微电位是指在一个非常小的区域内，电势的变化量。

微电位常常用于描述神经元活动、电化学反应、电化学传感器等领域中的电势变化。

在神经生理学中，微电位可以用来研究神经元的活动，从而揭示神经系统的工作机制。

在电化学反应中，微电位可以用来研究电化学反应的动力学过程，从而优化反应条件和提高反应效率。

在电化学传感器中，微电位可以用来测量各种离子或分子的浓度，从而实现对生物、化学、环境等领域的监测。

微电位的研究对于科学研究和技术应用具有重要意义。

首先，微电位可以帮助研究者更加准确地了解电势的变化规律，从而揭示电化学反应、神经系统等的工作机制。

其次，微电位可以用来设计和制造电化学传感器，实现对各种物质的灵敏检测。

此外，微电位还可以用来研究电化学储能、电化学合成等领域，为能源领域的发展提供新的思路和方法。

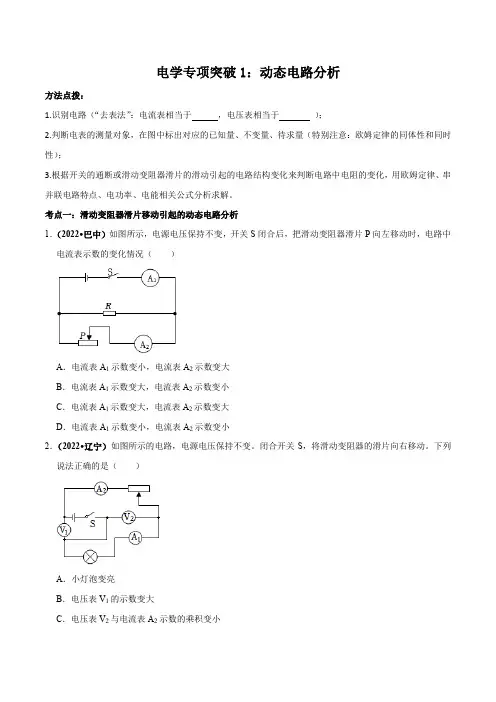
电学专项突破1：动态电路分析方法点拨：1.识别电路（“去表法”：电流表相当于，电压表相当于）；2.判断电表的测量对象，在图中标出对应的已知量、不变量、待求量（特别注意：欧姆定律的同体性和同时性）；3.根据开关的通断或滑动变阻器滑片的滑动引起的电路结构变化来判断电路中电阻的变化，用欧姆定律、串并联电路特点、电功率、电能相关公式分析求解。

考点一：滑动变阻器滑片移动引起的动态电路分析1．（2022•巴中）如图所示，电源电压保持不变，开关S闭合后，把滑动变阻器滑片P向左移动时，电路中电流表示数的变化情况（）A．电流表A1示数变小，电流表A2示数变大B．电流表A1示数变大，电流表A2示数变小C．电流表A1示数变大，电流表A2示数变大D．电流表A1示数变小，电流表A2示数变小2．（2022•辽宁）如图所示的电路，电源电压保持不变。

闭合开关S，将滑动变阻器的滑片向右移动。

下列说法正确的是（）A．小灯泡变亮B．电压表V1的示数变大C．电压表V2与电流表A2示数的乘积变小D．电压表V1与电流表A1示数之比不变3．（2022•通辽）如图所示电路，电源电压保持不变，开关S闭合后，在滑动变阻器滑片P向左移动的过程中，下列说法正确的是（）A．电压表V1示数变小，电压表V2示数不变，电流表A示数变小B．电压表V1示数变小，电压表V2示数变大，电压表V1的示数与电流表A的示数之比变小C．电压表V2示数不变，电流表A示数变大，电压表V1的示数与电流表A的示数之比变大D．电压表V1示数变小，电压表V2示数不变，电压表V2的示数与电流表A的示数之比变小4．（2022•遂宁）夏季汛期来临，某科技小组设计了一个监测观音湖水位的装置。

其原理如图甲，电路中电源电压保持不变，R0为定值电阻；R是竖直放置的长条形电阻片，浮子可带动金属滑杆AP在竖直方向上下移动，AP与R组成滑动变阻器（最大阻值60Ω），当电流表的示数达到某一数值时提醒监测员水位达到警戒值。

2017年第16期（总第256期）教育界/ EDUCATION CIRCLE▲课例评点电学变化量问题和力学变化量问题在中学物理中是典型变化量问题。

各地区在中考中凡是涉及此类问题，对学生来说都是比较难的。

不但学生对此类问题不好解答，失分高，对于教师来说在相关问题的教学上也感到很头疼。

在此，通过对两道变化量问题处理给大家提供一些思路。

例1：（2016·大连·14）如图所示，电源电压不变，闭合开关S ，滑动变阻器的滑片P 位于b 端，此时电阻R 1和R 2的功率相等，将滑动变阻器滑片P 从b 端滑到中点，下列说法正确的是（ ）A.电路的总电阻变小B.电阻R 1的功率小于电阻R 2的功率C.电阻R 1的电流变化量小于电阻R 2的电流变化量D.滑动变阻器的电流变化量小于电阻R 2的电流变化量【问题】这是典型的动态电路问题，学生存在问题：1.不知从滑动变阻器电阻变化入手利用整体和部分方法分析电路电阻变化；2.不会用串并联电路电压特点判断电阻两端的电压变化关系；3.不会由电压变化关系根据∆I =∆U /R 判断它们的电流变化关系。

【分析】1.由图知，R 与R 1并联再与R 2串联，根据滑片移动方向知R 连入阻值的变化，由串联和并联电路特点分析总电阻的变化；2.由滑片的移动方向知R 的连入电阻的变化，先判断并联部分的电阻变化，再根据串联电路的分压原理判断两部分电压变化，由P = U 2/R 和P 位于b 端时两电阻功率相等，可判断R 1与R 2的功率大小关系；3.由电路特点判断通过R 1与R 2的电流关系，由P =I 2R 和P 位于b 端时两电阻功率相等，判断两电阻的大小关系，由串联电路电压特点判断两电阻的电压变化关系，由欧姆定律判断两电阻的电流变化关系；4.由并联电路电压特点可知R 与R 1的电压变化关系，根据滑片移动知R 电阻的变化，由I = U /R 判断它们的电流变化关系。

本题考查了串联和并联电路特点、欧姆定律以及电功率公式的应用。

电学变化量的规律
1.定值电阻的阻值等于其两端电压变化量与电流变化量的比值，即 R=ΔU/ΔI,而滑动变阻器的阻值不等于其两端电压变化量与电流变化量的比值，即R滑≠ΔU/ΔI。

2.当电路中只有一个定值电阻与一个滑动变阻器时，移动滑片，定值电阻两端的电压变化量等于滑动变阻器两端的电压变化量。

3.当电路中有两个定值电阻与一个滑动变阻器时，移动滑片，滑动变阻器两端的电压变化量最大，且等于另两个定值电阻两端的电压变化量之和，而定值电阻阻值大的电压变化量也大，且电压变化量之比等于电阻之比。

4.当电压表测两个电阻的电压时，其示数变化量等于另一个电阻的电压变化量。

5.功率的变化量
（1）定值电阻的功率变化量ΔP ≠ΔU·ΔI，应根据R=ΔU/ΔI求出阻值，再跟据 P=U2/R或P=I2R 算出两次的功率，求差。

（2）总功率的变化量ΔP 总=U总·ΔI。