当前位置：文档之家 › 工程光学第三章

工程光学第三章

  • 格式：ppt
  • 大小：753.00 KB
  • 文档页数：88

下载文档原格式

  / 88

合集下载

工程光学第3章

工程光学第3章

tan U ' tan U n 1 n'
(3-21) (3-22) (3-23)
图3-19 nn时的节点
7
在同一介质中，f
'f
xJ f '
xJ ' f
平行于光轴的光线入射光学系统，当光学系统绕通过 像方节点J’的轴线摆动时，像点位置不变。
H J H' J' F'


H ' F ' H1 ' F1 ' F ' H 2 ' F1 ' H 2
f ' f ' 1 f 2 ' xF ' f 2
图3-22 两光组组合
f f ' xF ' 2 2
(3-25) (3-26)
f '
f1 ' f 2 '
(3-27) (3-28)
xF
近轴区适用的光学不变量(拉赫不变量)：
J nuy n ' u ' y '
像方焦距与 物方焦距之 比等于相应 相应 介质折射率 之比。
y y' ( f f ) tan U ( f ' f ') tan U ' y' y
fyu f ' y ' u ' f' n' f n fy tan U f ' y ' tan U '


1... i ... K
(3-12)
l tan U h l ' tan U '
( x f ) tan U ( x ' f ') tan U '

工程光学第二,三 章(合肥工业大学)

工程光学第二,三 章(合肥工业大学)
R/2
R
1.5 1 1.5 1 l '1 R
l1 ' 3R
图2-12a
即无穷远物体经第一面后成实像，是一个实物成实像的过 程，其像位于距玻璃球前表面的右侧3R处，同时位于距第 二面的右侧R处。由于第一面的像是第二面的物，又因为 其位于第二面的右侧，因此对于第二面而言是个虚物。
第一节 理想光学系统的共线理论
例3-1 如图3-1，已知Q、Q′为某理想光学 系统的一对共轭面， 并且已知该共轭面的垂 轴放大率，同时已知该系统的另外两对共轭 物像点C、C′和D、D′，试求图中任一物点P 的像点。
图 3-1
第一节 理想光学系统的共线理论
解：由P点过C点和D点分别作两条光线⑴和⑵，交Q 面于A点和B点,由于共轭面的垂轴放大率已知，根据 推论③，故容易得到Q′面上的A′点和B′点，即AB 和A′B′为这对共轭面上的一对共轭物像。根据推 论①，光线⑴的共轭光线⑴′必经过A′点和C′点， 光线⑵的共轭光线⑵′必经过B′点和D′点，得到 光线⑴′和⑵′的相交点P′,即为所求之像。
第四节 共轴球面系统的成像
l 2 l '1 d 3R 2R R ，r2 R 第二次成像， ' n2 1.5 ， n2 1
代入公式得
1 1.5 1 1.5 l2 ' R R
得 l2 ' R 2 即最终会聚于第二面的右侧 R 2 处，对第二 面而言，是一个虚物成实像的过程。
1 1 2 R 代入公式：l ' R R ，得 l 2 ' 2 3
R/2 R/3
R
即经第二面反射后成像于反射面左 图2-12b 侧 R 3 处，虚物成实像 第三次成像，光线从右到左，为了与符号规则一致，可将系统翻转 180°来计算第三次成像,此时有 l3 5R 3 , r3 R， n 1.5，n3 ' 1 1 1.5 1 1.5 代入公式得 l ' 5R / 3 R 得 l3 ' 5R / 2 2.5R

工程光学课件第03章

工程光学课件第03章

第三节 反射棱镜
（二）屋脊棱镜
奇数次反射使得物体成镜像，偶数次反射使物体成原像。 如果需得到与物体一致的像，而又不宜增加反射棱镜时，可用交线位 于棱镜光轴面内的两个相互垂直的反射面取代其中一个反射面，使垂直 于主截面的坐标被这二个相互垂直的反射面依次反射而改变方向，从而 得到物体的一致像。这两个相互垂直的反射面叫做屋脊面，带有屋脊面 的棱镜称为屋脊棱镜。 常用的屋脊棱镜有直角屋脊棱镜、半五角屋脊棱镜、五角屋脊棱镜、 斯密特屋脊棱镜等。
亦即同心光束经平行平板后变成了非同心光束。因此平行
平板不能成完善像。
L2 L1 L1 d
第二节 平行平板
二、平行平板的等效光学系统
平行平板在近轴区内以细光束成像时，由于I1及I1'都很小，其 余弦值可用1代替，于是近轴区内的轴向位移为
l d (1 1 )
n
平行平板在近轴区以细光束成像是
L
完善的。不管物体位置如何，其像 P
2
ß只与α有关
出射光线 不稳定
第二节 平行平板
一、平行平板的成像特性
n1 sin I1 n1 sin I1 n2 sin I2 n2 sin I2
B
n1 n2 1，n1 n2 n
I 2
I2
E
F
I1
nsisninI1I
2
n
s s
in in
I1 I 2
I1 U1 U2
A1( A2 ) A1 A2
（四）棱镜的组合——复合棱镜 1、分光棱镜
第三节 反射棱镜
2、分色棱镜
3、转向棱镜
第三节 反射棱镜
第三节 反射棱镜
第三节 反射棱镜
4、双像棱镜
第三节 反射棱镜

工程光学第3章

工程光学第3章
f f 通常用 表示，其符号遵从符号规则，像方焦距 的起算原点是像方
主点 。设入射光线AB的投射高度为h，出射光线 H
U
的孔径角为 E F
,由图可知
f = tgU
h
图2-5 像方焦点、像方主点和像方焦距
1.3 无限远轴外物点发出的光线
无限远轴外物点发出的、能进入光学系统的光线总是相互平行
1．理想光学系统理论
理想光学系统理论是在1841年由高斯所提出来的，所以理想光 学系统理论又被称为“高斯光学理论”。 （1）在理想光学系统中，任何一个物点发出的光线在系统的作 用下所有的出射光线仍然相交于一点，也就是说每一个物点对应于 唯一的一个像点。这种物像对应关系叫做“共轭”。 （2）如果光学系统的物空间和像空间都是均匀透明介质，则入 射光线和出射光线均为直线，根据光的直线传播定律，由点对应唯 一像点可推出直线成像为直线、平面成像为平面。这种点对应点、 直线对应直线、平面对应平面的理论称为共线成像理论。
图2-8 物方主面与像方之间的关系
一对主平面以及像方焦点 F 和物方焦点 F 称为共轴光学系统的基
点。它们构成了一个光学系统的基本模型，不同的光学系统，其基点
的相对位置不同，焦距不等。如果已知一个共轴光学系统的一对主平 面和两个焦点位置，它的成像性质就完全确定，所以，通常总是用一
对主平面和两个焦点位置来代表一个光学系统，如图2-9所示。
垂轴放大率、轴向放 大率、角放大率
三个放大率之间的关系； 多光组光学系统放大率与各
个光组放大率之间的关系
透镜
掌握透镜焦距的计算方法
透镜的分类； 正透镜和负透镜的焦距特点
把光学系统在近轴区成完善像的理论推广到任意大的空间，以任意 宽的光束都成完善像的光学系统称理想光学系统。本章主要介绍理想光 学系统的主要光学参数、成像关系和放大率、理想光学系统的光组组合 和透镜。

工程光学基础-第三章

工程光学基础-第三章

第一节 平面镜成像
P
三
、
双
I1
平
面
的 O2 I2
成 像
I2
A
I1
O1
q
P 由O1O2M 外角定理： 2I2 2I1 2 2(I1 I2 )
由O1O2N 外角定理：
I1 I2 q q (I1 I2 )
q
N
β=2θ
q
M
β≤90
P
第一节 平面镜成像
双平面镜的应用（两次反射棱镜）
两次反射棱镜就是双平面镜
作用：与屋脊垂直的坐标单独改变一次方向，相当于增加一次反射
第三节 反射棱镜
屋脊面的成像特性：
位于主截面内的物体，经屋 脊面后，其像与无屋脊面时所成 像一样，垂直于主截面的物体， 其像与无屋脊面时所成像相反 。增加一次反射，使系统总的 反射次数由奇数变成偶数，从 而达到物像相似的要求。
第三节 反射棱镜
2、二次反射棱镜
第三节 反射棱镜
1）半五角棱镜（α=22.5，β=45） 2）30直角棱镜（α=30，β=60） 以上两种多用于显微镜的转像系统
第三节 反射棱镜
——相当于夹角为 α的双平面镜系统，成一致像，入射光线与出射光线
夹角为2α x 光轴转1800
z y
z′ y′ x′
（a）等腰直角棱镜
(b)五角棱镜
（一）基本定义 第三节 反射棱镜
工作面 入射面、出射面、反射面
棱
工作面的交线
主截面 垂直于棱的截面 （光轴截面：主截面与光轴重合）
棱镜光轴：光学系统的光轴在 棱镜中的部分，如ABC
C
A
B
光轴长度：棱镜光轴的几何长度； 如AB+BC

大学工程光学第三章

大学工程光学第三章

达夫棱镜(只用于平行光路）
L 2nD 2n 2 1 1 2(2n 2 1) D 2n 2 1 1
L
d L cosi '
3.2平行平板
工程光学
平行平板是由两个相互平行的折射平面组成的光学零件
出射光线平行于入射光线，即光线经平行平板后方向 不变
d
l1
l2 '
l2 '
工程光学
1.棱镜展开后玻璃板的两个表面必须平行。
2.如果棱镜位于会聚光束中，则光轴必须和棱镜的入射 及出射表面相垂直。 如果棱镜位于平行光束中，则只要满足第一个要求。
L:光轴在棱镜中的长度 ( 一般即为等效平板的厚度 )
工程光学
一次反射等腰直角棱镜 L=D
二次反射等腰直角棱镜 L=2D
工程光学
五角棱镜
L＝3.414D
屋脊棱镜：对奇次反射的反射棱镜，为避免镜像，可 加一个屋脊。 两屋脊面的夹角必须等于90°
工程光学
由物坐标求像坐标 ： 原则：①光轴方向 z' 不变 ②垂直于主截面的坐标 x‘ 视屋脊个数而定， 无屋脊或屋脊为偶数个则x‘不改变方向，若屋脊为 奇数个则x‘反向。 ③ y‘ 坐标根据总反射次数而定（屋脊反射算 两次），奇数次反射成镜像，偶数次反射成一致像。
普罗Ⅱ型棱镜组
工程光学
别汉棱镜组
工程光学
角锥棱镜 角锥棱镜的三个反射面两两互成直角，使光线转过 180 度。
工程光学
工程光学
工程光学
2.棱镜的展开方法：在棱镜主截面内，按反射面的 顺序，以反射面与主截面的交线为轴，依次按反射 面顺序做镜像，便可得到棱镜的等效平行玻璃平板。
工程光学
为了使棱镜和共轴球面系统组合以后，仍然能保持共轴 球面系统的特性，必须对棱镜的结构提出一定的要求：

工程光学知识点整理

工程光学知识点整理

工程光学课件总结班级:姓名:学号:目录第一章几何光学基本原理 (1)第一节光学发展历史 (1)第二节光线和光波 (1)第三节几何光学基本定律 (3)第四节光学系统的物象概念 (6)第二章共轴球面光学系统 (7)第一节符号规则 (7)第二节物体经过单个折射球面的成像 (8)第三节近轴区域的物像放大率 (10)第四节共轴球面系统成像 (12)第二章理想光学系统 (14)第一节理想光学系统的共线理论 (14)第二节无限远轴上物点与其对应像点F’---像方焦点 (14)第三节理想光学系统的物像关系 1, 作图法求像 (17)第四节理想光学系统的多光组成像 (22)第五节实际光学系统的基点和基面 (25)第六节习题 (27)第四章平面系统 (27)第一节平面镜 (27)第二节反射棱镜 (28)第三节平行平面板 (29)第四节习题 (30)第五章光学系统的光束限制 (31)第一节概述 (31)第二节孔径光栅 (33)第三节视场光栅 (34)第四节景深 (35)第五节习题 (35)第八章典型光学系统 (36)第一节眼睛的光学成像特性 (36)第二节放大镜 (39)第三节显微镜系统 (41)第四节望远镜系统 (45)第五节目镜 (46)第六节摄影系统 (48)第七节投影系统 (49)第八节光学系统外形尺寸计算 (50)第九节光学测微原理 (53)第一章几何光学基本原理光和人类的生产活动和生活有着十分密切的关系, 光学是人类最古老的科学之一。

对光的每一种描述都只是光的真实情况的一种近似。

研究光的科学被称为“光学”（optics）, 可以分为三个分支:几何光学物理光学量子光学第一节光学发展历史1，公元前300年, 欧几里得论述了光的直线传播和反射定律。

2，公元前130年, 托勒密列出了几种介质的入射角和反射角。

3，1100年, 阿拉伯人发明了玻璃透镜。

4，13世纪, 眼镜开始流行。

5，1595年, 荷兰著名磨镜师姜森发明了第一个简陋的显微镜。

工程光学第三章共41页

工程光学第三章共41页
在O1O2N中, I1' I2 因此, 2
10
上述性质也可以结合单平面镜旋转成 像特点，很容易论证。
I
1
-I1’’
=2
11
根据这一性质，如果双面镜的夹角固定， 当入射光线方向一定时，双面镜绕其棱边 旋转时，出射光线方向始终保持不变。
这一性质用于双面镜折转光路非常有利， 其优点在于，只需加工并调整好双面镜的 夹角，而对双面镜的安置精度要求不高， 不像单个反射镜折转光路时调整困难。
2f'
测量微小位移:
y2f'2f'x2f'xKx
aa
其中,K为光学杠杆的放大倍数.
9
三、双平面镜成像
性质：在双平面镜系 统中，出射光线和入 射光线的夹角与入射 角无关，只取决于双 面镜的夹角α。 公式:β＝2α
N
M
QO
1
-I2’ -I1 I1’ I2
P
O
R
2
在O1O2M中, (I1I1')(I2 I2' ) 2(I1' I2)
TdsinI1(1tta an nII1 1 ')dsinI1(1n cc o o ssII11 ')
17
由像的位置 L' d(1 tan I1' ) 可知:
tan I1
轴向位移△L’随入射角I1，(即孔径角U1) 的不同而变化.
这表明:轴上点发出的不同孔径的光线经 平板后与光轴的交点不同。因此,平行平板 不能成完善像。
tanU 1
15
➢光线经平行平板后方向不变； ➢平板是个无光焦度元件，
不会使物体放大或缩小， 在系统中对光焦度无贡献。
16
光线经平行平板后，产生侧向位移△T和

(工程光学教学课件)第3章 平面与平面系统

(工程光学教学课件)第3章 平面与平面系统

半透半反膜
蓝光
红光
100%
50%
50%
分光棱镜
白光
ab
绿光
分色棱镜
转像棱镜
➢ 主要特点：出射光轴与入射光轴平行，实现完全倒像，并能折转很 长的光路在棱镜中。
➢ 应用：可用于望远镜光学系统中实现倒像。
x y
z
x
x z y
y z
y z
x x
yz
y z x
a) 普罗I型转像棱镜
b) 普罗II型转像棱镜
图 3-18 转像棱镜
将玻璃平板的出射平面及出射光路HA一起沿光轴平移l，则CD与EF重合，出射光线
在G点与入射光线重合，A与A重合。
PA
Байду номын сангаас
EC
这表明:光线经过玻璃平板的光路与无折射的通过 空气层ABEF的光路完全一样。这个空气层就称为 平行平板的等效空气平板。其厚度为：
Q
H
G
A
A
l
ddld/n
L
B d FD
d
例题：一个平行平板，折射率n=1.5，厚度d，一束会聚光入射，定点为M ，M距平行平板前表面的距离为60mm，若此光束经平行平板成像与M‘， 并且有M’与M相距10/8mm，求厚度d
l' d (1 1 ) n
n=1.5，Δl’=10/8
M M’ d
§3-3 反 射 棱 镜 B
一、反射棱镜的类型
O1
➢ 反射棱镜的概念：
Q
P
将一个或多个反射面磨制在同一块玻璃上
形成的光学元件称为反射棱镜。
➢ 反射棱镜的作用：
O2 A
折转光路、转像和扫描等。
R
➢ 反射棱镜的术语：

工程光学第三章课件

工程光学第三章课件
两个相互垂直的反射 面称为屋脊面。 带有屋脊面的棱镜称 为屋脊棱镜。
41
分类
➢屋脊棱镜
x
*作用
yz
不增加反射棱镜，不改变 光轴方向和主截面内成像 方向。
增加一次反射（垂直于主
截面方向），使系统总反 y 射次数由奇数变成偶数， 达到物像一致。
xʺ
yʺ
zʺ
x yz
xʹ yʹ zʹ
45°
yʹ
y
xʺ zʺ
双平面镜
➢练习
*两个相互倾斜放置的平面镜M1、M2构成一个双平面镜
系统，现一条光线平行于其中一个镜面入射，并先后 在所M示1。、M2之间经过四次反射后正好沿原路返回，如图
求两平面镜之间的夹角α。
4α
M2
18
双平面镜
➢练习
*入入射射光光线线的经偏M1转、角M度2依为次2反α；射当2次经后过，两出个射反光射线面相依对次于反
2f
10
单平面镜
➢旋转效应（倍角关系）
*应用：测量微小角度或位移变化。（光学杠杆原理）
② 微小位移变化
y 2 f 2 f x
a 2 f x Kx
a x y ay
K 2f
11
单平面镜
➢平移效应
*物保持不动，平面镜向靠近/远离物的方向平移距离h，
则像沿着相同方向平移距离2h。

A
Q
A1ʹ
A
P Q
2
A PR A2 PQ A2
APA2 QPR QPA2 RPA

A2ʺ
*角度：物A绕棱边（旋转
轴）旋转角度2α。
*方向：从第一反射面转向

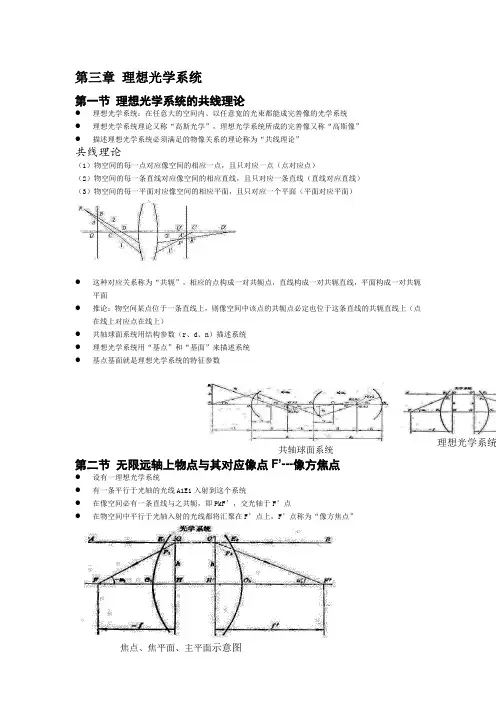
工程光学第三章知识点

工程光学第三章知识点

理想光学系统第三章 理想光学系统第一节 理想光学系统的共线理论● 理想光学系统：在任意大的空间内、以任意宽的光束都能成完善像的光学系统 ● 理想光学系统理论又称“高斯光学”，理想光学系统所成的完善像又称“高斯像” ●描述理想光学系统必须满足的物像关系的理论称为“共线理论”共线理论（1）物空间的每一点对应像空间的相应一点，且只对应一点（点对应点）（2）物空间的每一条直线对应像空间的相应直线，且只对应一条直线（直线对应直线） （3）物空间的每一平面对应像空间的相应平面，且只对应一个平面（平面对应平面）● 这种对应关系称为“共轭”，相应的点构成一对共轭点，直线构成一对共轭直线，平面构成一对共轭平面● 推论：物空间某点位于一条直线上，则像空间中该点的共轭点必定也位于这条直线的共轭直线上（点在线上对应点在线上）● 共轴球面系统用结构参数（r 、d 、n ）描述系统 ● 理想光学系统用“基点”和“基面”来描述系统 ● 基点基面就是理想光学系统的特征参数第二节 无限远轴上物点与其对应像点F ’---像方焦点● 设有一理想光学系统● 有一条平行于光轴的光线A1E1入射到这个系统● 在像空间必有一条直线与之共轭，即PkF’，交光轴于F’点●在物空间中平行于光轴入射的光线都将汇聚在F’点上，F’点称为“像方焦点”共轴球面系统焦点、焦平面、主平面示意图焦点、焦平面、主平面示意图● 过F’点作垂直于光轴的平面，称为“像方焦平面” ● 像方焦平面与物方无限远处垂直于光轴的物平面共轭● 物方的任何平行光线若不与光轴平行，表示无限远处的轴外点，将汇聚在像方焦平面上的一点2，无限远的轴上像点和它所对应的物方共轭点F ——物方焦点● 像方平行于光轴的光线，表示像方光轴上的无限远点● 在物方光轴上必定有一点F 与之共轭，F 点称为物方焦点，过F 点的垂轴平面称为物方焦平面 ● 物方焦点F 与像方焦点F’不是一对共轭点3，垂轴放大率β=+1的一对共轭面——主平面● 在光学系统中存在着垂轴放大率β=+1的一对共轭平面，这一对共轭面称为“主平面”即物方主平面和像方主平面● 共轭垂轴平面QH 和Q’H’满足β=+1（因为高度h 相等） ● QH 为物方主平面，Q’ H’为像方主平面 ● H 为物方主点，H’为像方主点 ● 物方主平面QH 与像方主平面Q’H’共轭 ● 物方主点H 与像方主点H’共轭● 对于理想光学系统，不论其实际结构如何，只要知道了主点和焦点的位置，其特性就完全被决定了 4，光学系统焦距● 像方焦距：像方主点H ’到像方焦点F ’的距离f ’ ● 物方焦距：物方主点H 到物方焦点F 的距离f●焦距均以各自的主点为原点，与光线传播方向一致为正，相反为负 光学系统的焦距计算式tan tan h f U h f U '='=焦距包含了光学系统主点和焦点的相对位置，是描述光学系统性质的重要参数 像方焦距f ’>0的光组称为正光组，f ’<0的光组称为负光组无限远轴外物点的共轭像点焦点、焦平面、主平面示意图当光学系统的物方与像方处于同一介质中时，物方焦距与像方焦距数值相等，符号相反f = -f ’单折射球面的主平面和焦点共轴球面系统的成像性质可以用一对主平面和两焦点表示，为此目的，先研究单个折射球面的主平面和焦点位置。

工程光学基础教程 习题参考答案

工程光学基础教程 习题参考答案

第一章 几何光学基本定律1. 已知真空中的光速c ＝3810⨯m/s ，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25 m/s, 当光在冕牌玻璃中，n=1.51时，v=1.99 m/s, 当光在火石玻璃中，n ＝1.65时，v=1.82 m/s ， 当光在加拿大树胶中，n=1.526时，v=1.97 m/s ，当光在金刚石中，n=2.417时，v=1.24 m/s 。

2. 一物体经针孔相机在 屏上成一60mm 大小的像，若将屏拉远50mm ，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x ，则可以根据三角形相似得出：,所以x=300mm即屏到针孔的初始距离为300mm 。

3. 一厚度为200mm 的平行平板玻璃（设n =1.5），下面放一直径为1mm 的金属片。

若在玻璃板上盖一圆形的纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片的最小直径应为多少？2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ，包层的折射率为2n ，光纤所在介质的折射率为0n ，求光纤的数值孔径（即10sin I n ，其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有： n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上，求其会聚点的位置。

工程光学第三章平面与平面系统

工程光学第三章平面与平面系统

（二）屋脊棱镜
问题：要得到物体的一致像，而又不宜增加反射棱镜时，如 何解决奇数次反射使物体成镜像的问题？
解决方法：用交线位于棱镜光轴面内的两个相互垂直的反射 面取代其中一个反射面，使垂直于主截面的坐标被这两个相互 垂直的反射面依次反射而改变方向 ，从而得到物体的一致像 （偶数次反射成像）。 屋脊面 —— 这两个相互垂直的反射面叫做屋脊面，带有屋脊 面的棱镜称为屋脊棱镜。
2
（3-4）
根据这一性质，用双面镜折转光路非常有利，其优点：只需 加工并调整好双面镜的夹角 ( 如两个反射面做在玻璃上形成棱 镜 )，而对双面镜的安置精度要求不高，不像单个反射镜折转光 路时存在调整困难。
D
潜望高度 可将成像光束平 移一段距离D
1 2
(a)
M2 A2
3 4 o1
屋脊面，屋脊 双反射镜，入 射光线方向与 出射光线方向 相互平行。成 像光束转180°
本章内容：

平面镜成像 平行平板 反射棱镜 折射棱镜与光楔 光学材料
本章重点： ★ 反射棱镜成像方向的确定 ★ 等效空气平板 ★ 光楔
第一节 平面镜成像
一、平面镜成像 平面反射镜又称平面镜，是光学系统中最简单、而 且也是唯一能成完善像的光学元件，即同心光束经平 面镜反射后仍为同心光束。
这表明 ，光线经过玻璃平板的光路与无折射的通过空气层 ABEF的光路完全一样。这个空气层就称为玻璃平板的等效空气 平板，其厚度为： （3-9） d d - l ' d n
引入等效空气平板的作用在于：如果光学系统的会聚或发散光 路中有平行平板 ( 也可能由棱镜展开而成 )，可将其等效为空气平 板，这对光学系统的外形尺寸计算将非常有利，只需计算出无平 行平板时的像方位置，然后再沿轴向移动一个轴向位移Δl’，就得 到有平行平板时的实际像面位置，即

工程光学知识点整理

工程光学知识点整理

工程光学课件总结班级：姓名：学号：目录第一章几何光学基本原理 (1)第一节光学发展历史 (1)第二节光线和光波 (1)第三节几何光学基本定律 (3)第四节光学系统的物象概念 (5)第二章共轴球面光学系统 (6)第一节符号规则 (6)第二节物体经过单个折射球面的成像 (7)第三节近轴区域的物像放大率 (10)第四节共轴球面系统成像 (11)第二章理想光学系统 (13)第一节理想光学系统的共线理论 (13)第二节无限远轴上物点与其对应像点F’---像方焦点 (14)第三节理想光学系统的物像关系 1，作图法求像 (17)第四节理想光学系统的多光组成像 (21)第五节实际光学系统的基点和基面 (25)第六节习题 (27)第四章平面系统 (27)第一节平面镜 (27)第二节反射棱镜 (28)第三节平行平面板 (30)第四节习题 (31)第五章光学系统的光束限制 (31)第一节概述 (31)第二节孔径光栅 (33)第三节视场光栅 (34)第四节景深 (35)第五节习题 (36)第八章典型光学系统 (36)第一节眼睛的光学成像特性 (36)第二节放大镜 (39)第三节显微镜系统 (40)第四节望远镜系统 (44)第五节目镜 (46)第六节摄影系统 (47)第七节投影系统 (49)第八节光学系统外形尺寸计算 (49)第九节光学测微原理 (52)第一章几何光学基本原理光和人类的生产活动和生活有着十分密切的关系，光学是人类最古老的科学之一。

对光的每一种描述都只是光的真实情况的一种近似。

研究光的科学被称为“光学”（optics），可以分为三个分支：几何光学物理光学量子光学第一节光学发展历史1，公元前300年，欧几里得论述了光的直线传播和反射定律。

2，公元前130年，托勒密列出了几种介质的入射角和反射角。

3，1100年，阿拉伯人发明了玻璃透镜。

4，13世纪，眼镜开始流行。

5，1595年，荷兰著名磨镜师姜森发明了第一个简陋的显微镜。

第3章工程光学

第3章工程光学

在近轴区域内，光学系统能成完善像。
E
lu l ' u ' h
A
-u -l
h O D l′
u′
A′
非理想光学系统
11
理想光学系统
12
2
3.1.1 理想光学系统的共线理论
理想光学系统理论又称之为高斯光学，其基本核心是共线成像。所谓共 线成像，就是指在理想光学系统中的一一对应关系：任一物点在像空间都 有一个和它唯一对应的像点；物空间任一条直线，则在像空间也有对应的 唯一直线；物空间任一平面，像空间也有唯一的对应平面，这种点对应点、 直线对应直线、平面对应平面的成像变换即称之共线成像，这种物像一一 对应的关系称之为共轭关系。 按照这一理论，可以得到如下推论： ① 如果一条物方光线经过物点P，则对应的像方光线必经过其共轭点P′； ② 如果物方的平面垂直于光轴，则像方的共轭平面也垂直于光轴； ③ 在任何一对共轭的垂轴平面内，垂轴放大率为一常数，即垂轴的平面物 体物像相似。
3.2.3 物方主平面与像方主平面间的关系
由符号规则确定。如果由F发出的入射光线的孔径角为U。其相应的出射 光线在物方主平面上的投射高度为h,由图2-7的三角几何关系有
f h tgU
在图中，作出一投射高度为h且平行于光轴的光线入射到理想光学系统，相应的出射光线必通
Q F H
23
过像方焦点 F’；过物方焦点 F 作一条入射光线，并且调整这条入射光线的孔径角，使得相 应出射光线的投射高度也是h。这样，两条入射光线都经过 Q点，相应的两条出射光线都经过 Q’，所以 Q 与 Q’就是一对共轭点，物方主面与像方主面是一对共轭面，而且 QH 与 Q’H’ 相等并在光轴的同一侧，所以，一对主平面的垂轴放大率为+1，即一对共轭光线在相应主面 上的投射高度相等。这一性质在用作图法追迹光线时是非常有用的。

工程光学习题参考答案第三章平面与平面系统

工程光学习题参考答案第三章平面与平面系统

第三章 平面与平面系统1. 人照镜子时，要想看到自己的全身，问镜子要多长？人离镜子的距离有没有关系？ 解：镜子的高度为1/2人身高，和前后距离无关。

2有一双面镜系统，光线平行于其中一个平面镜入射，经两次反射后，出射光线与另一平面镜平行，问两平面镜的夹角为多少？ 解：OA M M //32 3211M M N M ⊥∴1''1I I -= 又 2''2I I -=∴α同理：1''1I I -=α 321M M M ∆中 ︒=-+-+180)()(1''12''2I I I I αAOBM 1M 2M 3 N1N 2-I 1 I ''1-I 2I ''2 αααα︒=∴60α 答：α角等于60︒。

3. 如图3-4所示，设平行光管物镜L 的焦距'f =1000mm ，顶杆离光轴的距离a =10mm 。

如果推动顶杆使平面镜倾斜，物镜焦点F 的自准直象相对于F 产生了y =2mm 的位移，问平面镜的倾角为多少？顶杆的移动量为多少？ 解：θ'2f y = rad 001.0100022=⨯=θ αθx=mm a x 01.0001.010=⨯=⨯=∴θ图3-44. 一光学系统由一透镜和平面镜组成，如图3-29所示。

平面镜MM 与透镜光轴垂直交于D点，透镜前方离平面镜600mm 有一物体AB ，经透镜和平面镜后，所成虚像''A ''B 至平面镜的距离为150mm,且像高为物高的一半，试分析透镜焦距的正负，确定透镜的位置和焦距，并画出光路图。

图3-29 习题4图解： 由于平面镜性质可得''B A 及其位置在平面镜前150mm 处 ''''B A 为虚像,''B A 为实像则211-=β 21'1-==L L β 450150600'=-=-L L 解得 300-=L 150'=L 又'1L -L 1='1f mm f 150'=∴ 答：透镜焦距为100mm 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

此性质可用于棱镜转像（降低安装要求）
证明：
从△O1O2M得：（不考虑符号）
2I1＝2I2＋β β＝2（I1－I2）
从△O1O2N得：
I1－I2＝α ∴β＝2α（与I1无关）
N

M
2、成一致像：右→左→右
Q
O1
I2
P
I2

A I1 I1
R
O2 Q1
图3-5 双平面镜对光线的变换
第二节 平行平板
棱镜的结构参数 在光路计算中，常要求出棱镜光轴长 度，即棱镜等效平板厚度L。设棱镜的口径为D，则棱镜 光轴长度L与口径D之间关系为：L＝KD 式中K取决于棱 镜的结构形式，与棱镜的大小无关，因此称为棱镜的结 构参数。
（二）几种典型棱镜的展开
１、直角棱镜
２、道威棱镜 ３、五角棱镜
４、等腰棱镜
５、半五角棱镜 ６、斯密特棱镜
Q
O1 B
P
R O2
A
图3-9 反射棱镜的主截面
一、反射棱镜的类型：
反射棱镜种类繁多，形状名异，大体上可分为简单 棱镜、屋脊棱镜、立方角锥棱镜和复合棱镜四类，下面 分别予以介绍。
（一）简单棱镜：
简单棱镜只有一个主截面，它所有的工作面都与主截 面垂直。根据反射面数的不同，又分为一次反射棱镜、二 次反射棱镜和三次反射棱镜。
第三章 平面与平面系统
平面光学元件的分类： 平面反射镜、平行平板、反射棱镜、折射棱镜、光楔。
平面光学元件的作用： 转像、光路转折、产生色散（用于光谱分析）等。
第一节 平面镜成像
一、单平面镜的成像特性：
1. 物、像大小相等，
位置对称于镜面，
成完善像。
l l, 1
B
2. 物、像虚实相反。 N
z'
L
x'' y''
y' x' z'
L x'' y''
z''
x'''
z''
x'''
z'''
z'''
P3
y'''
P3
y'''
图3-11 周视瞄准仪光路图
三、反射棱镜的等效作用与展开
（一）棱镜的等效作用与展开方法 反射棱镜有两个折射面和若干个反射面组成，所起的
作用相当于平面镜，主要是折转光路和转像的作用。如果 不考虑棱镜的反射面作用，光线在两折射面间的行为可等 效于一个平行平板。
四．双平面镜成像
N

M
1、入射光线经双面镜连续
反射一次后，其出射光线
Q
O1
将偏转2 （ —双面镜夹角），
I2
I2

P
即出射光线与入射光线
A I1 I1
的夹角 与入射角的大小
R
O2 Q1
无关，仅与 有关。
图3-5 双平面镜对光线的变换
（应用:双面镜绕其棱边转动时出射光线方向不变）
I1 I2 U1 U2
tanU2 1, 1 1, 2 1
tanU1

平行平板是无光焦度元件,不会使物体放大或缩小.
1、侧向位移：△T
T DG DE sin(I2 I2 )
I2 I1, I2 I1
d DE
cos I1
。 45
X
O
Y
双像棱镜
二、棱镜系统的成像方向判断
判断原则： （１）O’z’坐标轴：和光轴的出射方向一致。 （２）垂直于主截面的坐标轴O’y’：视屋脊面的个数而 定，如果有奇数个屋脊面，则其像坐标轴方向与物坐标轴 Oy方向相反；没有屋脊面，则像坐标轴方向与物坐标轴坐 标轴方向一致。 （３）平行于主截面的坐标轴O’x’：视反射面个数（屋 脊面算两个反射面）而定。如果物坐标系为右手坐标系， 当反射面个数为偶数时， O’x’坐标轴按右手坐标系确定； 而当反射面个数为奇数时，O’x’坐标轴依左手坐标系确 定。
１、一次反射棱镜 与单个平面镜对应，使物体成镜像， 即垂直于主截面的坐标方向不变，位于主截面内的坐标改 变方向。
对于简单棱镜，在主截面内的坐标改变方向，垂直于 主截面的坐标不改变方向， O'z'始终沿出射光轴方向。
x yz
x'
y'
z' a)
等腰直角棱镜
x' z'
y'
z yx
b)
等腰棱镜
x yz
x yz
求：d1
解： d1 (l l1) d
l
d1
l1
d
l d(1 1) 3.42mm n
∴d1＝3.42＋18.75－10＝12.17mm
例2：平板微动装置
A
A" △Z A'
d
侧向位移：△Z＝d（1－1/n）
二、等效空气板： 意义：在外形尺寸计算中，可先把玻璃平板当成空
Q
O
图3-3 平面镜旋转
Q1
应用：光杆杠原理(光学比较仪)微小角度或位移的测量 A′
y
a
FA
20
f'
0
x
图3-4 平面镜用于小角度或位移测量
y AA f tan 2 2 f x a tan a
k AA f tan 2 2 f x a tan a
——放大倍数
例：f1＝200㎜
a＝5㎜ 则 k＝80
y 2fx a
测微小位移:
x ya 2f
y f tan 2 2 f 测微小角度: y
2f
三．平面镜的平移性质 A
h A1
2h A11
AA AA AA AA 2( AA h) 2h 2
A
R
-I''
I
QB
PB O Q
P
图3-1 平面镜成像
B' A'
3. 成镜像：右手坐标系→左手坐标系
正对物体沿zO方向观察，y→x:顺时为右，逆时为左。
Y轴在左边, Y′轴在右边.（奇数次反射成镜像，偶数次
反射成一致像）
x'
4.当物体旋转时,其像反向旋转相同的角度
x
P
z'
y'
z O
y
M
图3-2 平面镜的镜像
x
z O
y
x
z O
y
y z
O x
x y
z O
z
O
y
x
二．平面镜的旋转性质 入射光线不变，当平面镜转动α角， 出射光线按相同方向转2α角。
证明：
I1 (I ) I1 I
(I ) I 2
P1 a p
N a N1 I1
-I''1 I -I'' 0=2a
30° 60°
半五角棱镜和 30°直角棱镜多用于显微镜观察系统
x
y
x
x yz
yz
y' z'
45°
x'
五角棱镜
直角棱镜
45°、90°
90°、180°
五角棱镜取代一次反射角棱镜或平面镜，使光
轴折转90°，而不产生镜像，且装调方便。
二次反射直角棱镜多用于转像系统中
x
yz
45°
斜方棱镜 180°360°
E I'2 F
n'2=1
O2
l2 l1 d l
第三节 反射棱镜
基本概念 将一个或多个反射面磨制在同一玻璃上的光学元件
称为反射棱镜，在光学系统中主要用于折转光路、转像、 倒像和扫描等。
光轴:光学系统的光轴在棱镜中的部分称为棱镜的光轴
，一般为折线，如图3-9中AO1、O1O2、和O2B。每经过
（二）屋脊棱镜 我们知道，奇数次反射使得物体成镜像。如果需
得到物体一致像，而又不宜增加反射棱镜时，可用交 线位于棱镜光轴面内的两个相互垂直的反射面取代其 中一个反射面，使垂直于主截面的坐标被这二个相互 垂直的反射面依次反射而改变方向，从而得到物体的 一致像（偶数次反射成像），如图3-14所示。这两个 相互垂直的反射面叫做屋脊面，带有屋脊面的棱镜称 为屋脊棱镜。
分划板，保护玻璃，反射棱镜（展开）
n1=1 I1
-U'1
A'1(A2)
A
-L'1
-U1 A'2
L'
-L1
-L2
D
I2
G -U'2 O1
n2=n'1=n
d -L'2
E I'2 F
n'2=1
O2
图3-7 平行平板的成像特性
一．成像特征
二折射面平行 I1 I2 sin I1 n sin I1 n sin I2 sin I2
A' F'
Le
R
Q
D P -d L
F'' A'' R'
图3-20 反射棱镜的等效作用
在光路计算中，常用一等效平行玻璃平板平取代光线 在反射棱镜两折射面之间的光路，这种做法称为棱镜的展 开。
棱镜展开方法：在棱镜主截面内，按反射面的顺序，以 反射面与主截面的交线为轴，依次按反射面顺序作镜像， 便可得到棱镜的等效平行平板。需要说明的是，若棱镜位 于非平行平板不垂直光轴，引起侧向位移，影响光学系统 成像质量。