《机械工程测试技术基础(第4版)》基本课件 第1章 绪论
- 格式:pptx
- 大小:362.18 KB
- 文档页数:39

第一章绪论1、测试的概念目的:获取被测对象的有用信息。
测试是测量和试验的综合。
测试技术是测量和试验技术的统称。
2、静态测量及动态测量静态测量:是指不随时间变化的物理量的测量。
动态测量:是指随时间变化的物理量的测量。
3、课程的主要研究对象研究机械工程中动态参数的测量4、测试系统的组成5、量纲及量值的传递6、测量误差系统误差、随机误差、粗大误差7、测量精度和不确定度8、测量结果的表达第二章信号分析及处理一、信号的分类及其描述1、分类2、描述时域描述:幅值随时间的变化频域描述:频率组成及幅值、相位大小二、求信号频谱的方法及频谱的特点1、周期信号数学工具:傅里叶级数方法:求信号傅里叶级数的系数频谱特点:离散性谐波性收敛性(见表1-2)周期的确定:各谐波周期的最小公倍数基频的确定:各谐波频率的最大公约数2、瞬变信号(不含准周期信号)数学工具:傅里叶变换方法:求信号傅里叶变换频谱特点:连续性、收敛性3、随机信号数学工具:傅里叶变换方法:求信号自相关函数的傅里叶变换频谱特点:连续性三、典型信号的频谱1、δ(t)函数的频谱及性质△(f)=1 频率无限,强度相等,称为“均匀谱”采样性质:积分特性:卷积特性:2、正、余弦信号的频谱(双边谱)欧拉公式把正、余弦实变量转变成复指数形式,即一对反向旋转失量的合成。
解决了周期信号的傅里叶变换问题,得到了周期信号的双边谱,使信号的频谱分析得到了统一。
3、截断后信号的频谱频谱连续、频带变宽(无限)四、信号的特征参数1、均值:静态分量(常值分量)正弦、余弦信号的均值?2、均方值:强度(平均功率)均方根值:有效值3、方差:波动分量4、概率密度函数:在幅值域描述信号幅值分布规律五、自相关函数的定义及其特点1、定义:2、特点3、自相关图六、互相关函数的定义及其特点1、定义2、特点3、互相关图七、相关分析的应用八、相关系数及相干函数相关系数、相关函数在时域描述两变量之间的相关关系;相干函数在频域描述两变量之间的相关关系。




机械工程测试技术基础引言机械工程领域的发展需要依赖于有效的测试技术来保证产品的质量和性能。
机械工程测试技术基础是机械工程师必备的知识之一。
本文将介绍机械工程测试技术的基础知识,包括测试方法、测试设备、测试流程等方面的内容。
测试方法测试方法是机械工程测试的核心。
它包括了对产品的性能、质量和可靠性进行定量和定性的评估。
常用的机械工程测试方法有静态测试和动态测试两种。
静态测试静态测试是通过对物体的外部形态、尺寸、质量等特征进行测试。
这种测试方法一般可以通过目测、测量仪器等手段进行。
静态测试的目的是评估产品的静态性能,如刚度、强度、硬度等。
例如,在机械设计过程中,可以通过有限元分析等静态测试方法来评估产品的刚性和强度。
动态测试动态测试是通过给予物体外部力或运动状态下对其进行测试。
这种测试方法可以评估产品在不同运动状态下的性能和可靠性。
动态测试常用的方法有冲击测试、振动测试等。
例如,在机械工程领域中,可以通过振动台等设备对产品进行振动测试,以评估产品在振动环境下的可靠性和耐久性。
测试设备机械工程中常用的测试设备有很多种,根据不同的测试方法和需求,选择适合的测试设备非常重要。
传感器传感器是机械工程测试中常用的设备之一。
它们可以用来测量物体的尺寸、形态、力量、速度等各种参数。
常见的传感器包括压力传感器、温度传感器、加速度传感器等。
传感器可以通过物理或电子方式将测试对象的特征转换为可读取的信号,进而进行数据分析和判读。
试验台试验台是机械工程测试中的另一个重要设备。
它可以提供稳定的工作台面和固定测试物体的能力。
试验台的设计要考虑到测试对象的大小、稳定性和安全性等因素。
试验台的种类很多,例如万能材料试验机、振动台、冲击试验台等。
根据具体的测试需求和要求,选择适用的试验台非常关键。
数据采集装置数据采集装置是机械工程测试中必不可少的设备。
它可以将传感器采集到的数据转化为数字信号,并保存或传输到计算机进行分析。
数据采集装置的功能包括数据采集、数据存储和数据传输等。
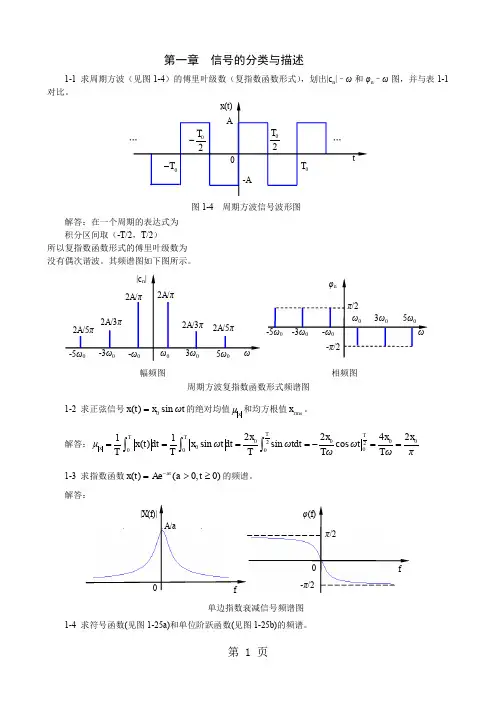
第一章 信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
解答:在一个周期的表达式为 积分区间取(-T/2,T/2)所以复指数函数形式的傅里叶级数为 没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。
解答:00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T TT ωT ωπ====-==⎰⎰⎰1-3 求指数函数()(0,0)atx t Ae a t -=>≥的频谱。
解答:1-4 求符号函数(见图1-25a)和单位阶跃函数(见图1-25b)的频谱。
单边指数衰减信号频谱图A /aπ/2-π/2幅频图相频图周期方波复指数函数形式频谱图图1-4 周期方波信号波形图a)符号函数的频谱t =0处可不予定义,或规定sgn(0)=0。
该信号不满足绝对可积条件,不能直接求解,但傅里叶变换存在。
可以借助于双边指数衰减信号与符号函数相乘,这样便满足傅里叶变换的条件。
先求此乘积信号x 1(t)的频谱,然后取极限得出符号函数x (t )的频谱。
b)阶跃函数频谱在跳变点t =0处函数值未定义,或规定u (0)=1/2。
阶跃信号不满足绝对可积条件,但却存在傅里叶变换。
由于不满足绝对可积条件,不能直接求其傅里叶变换,可采用如下方法求解。
解法1:利用符号函数结果表明,单位阶跃信号u (t )的频谱在f =0处存在一个冲激分量,这是因为u (t )含有直流分量,在预料之中。
同时,由于u (t )不是纯直流信号,在t =0处有跳变,因此在频谱中还包含其它频率分量。
解法2:利用冲激函数 根据傅里叶变换的积分特性单位阶跃信号频谱f|U (f )|(1/2)1()sgn()at x t e t -=符号函数tx 1(t ) 01-1符号函数频谱图1-25 题1-4图a)符号函数b)阶跃函数1-5 求被截断的余弦函数0cos ωt (见图1-26)的傅里叶变换。


