五年级下册数学试题-体积表面积的变化(无答案)沪教版
- 格式:doc
- 大小:40.00 KB
- 文档页数:4
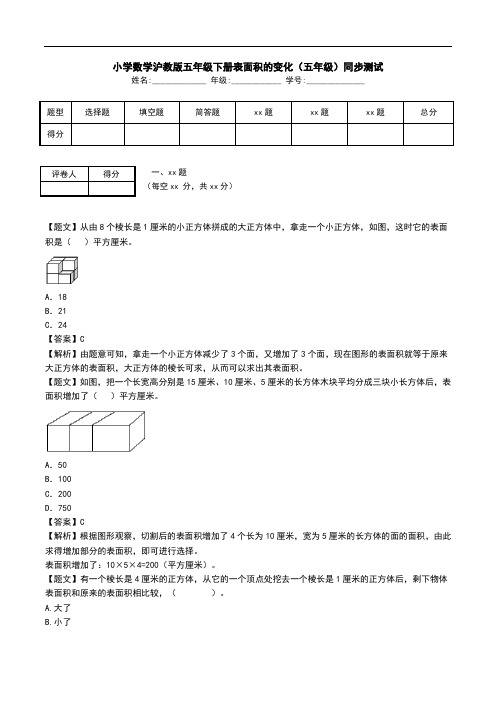
小学数学沪教版五年级下册表面积的变化(五年级)同步测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】从由8个棱长是1厘米的小正方体拼成的大正方体中,拿走一个小正方体,如图,这时它的表面积是()平方厘米。
A.18B.21C.24【答案】C【解析】由题意可知,拿走一个小正方体减少了3个面,又增加了3个面,现在图形的表面积就等于原来大正方体的表面积,大正方体的棱长可求,从而可以求出其表面积。
【题文】如图,把一个长宽高分别是15厘米、10厘米、5厘米的长方体木块平均分成三块小长方体后,表面积增加了()平方厘米。
A.50B.100C.200D.750【答案】C【解析】根据图形观察,切割后的表面积增加了4个长为10厘米,宽为5厘米的长方体的面的面积,由此求得增加部分的表面积,即可进行选择。
表面积增加了:10×5×4=200(平方厘米)。
【题文】有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,剩下物体表面积和原来的表面积相比较,()。
A.大了B.小了评卷人得分C.不变D.无法确定【答案】C【解析】根据观察可得:挖去小正方体后,减少三个面,同时又增加三个面,其实剩下的图形的表面积与原正方体的面表积是相等的。
【题文】如图是一个长3厘米,宽与高都是2厘米的长方体,在它的上面挖掉一个棱长为1厘米的小正方体,这时它的表面积是()平方厘米。
A.32B.34C.不能计算【答案】B【解析】由图意可知:在它的上面挖掉一个棱长为1厘米的小正方体,则增加了小正方体的2个面的面积,于是利用正方体的表面积加上小正方体的2个面的面积,问题即可得解。
3×2×4+2×2×2+(2÷2l【答案】D【解析】由题意得:减少部分是这个正方体的两个面的面积,由此解答出正确的结果,即可得出正确答案。





2022-2023学年五年级数学下册典型例题系列之期末典例专项练习七:表面积的增减变化问题(解析版)一、填空题。
1.有一个长方体,如果长减少2厘米,就变成一个正方体,正方体的表面积是96平方厘米,原来长方体的长是( )厘米,体积是( )立方厘米。
【答案】 6 96【分析】根据正方体的表面积=棱长×棱长×6,用96÷6即可求出正方体一个面的面积,进而求出正方体的棱长,也就是长方体原来的宽和高,根据题意可知,长方体原来的长比正方体的棱长多2厘米,据此求出长方体的长,然后根据长方体体积公式:长方体的体积=长×宽×高求出长方体的体积。
【详解】96÷6=16(平方厘米)16=4×4长方体的宽和高是4厘米,长方体的长:4+2=6(厘米)长方体的体积:6×4×4=96(立方厘米)原来长方体的长是6厘米,体积是96立方厘米。
【点睛】本题考查了长方体体积公式和正方体表面积公式的灵活应用,关键是熟记公式。
2.用两个棱长是5分米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方分米。
【答案】250【分析】根据题意,用两个棱长是5分米的正方体拼成一个长方体,那么拼成的长方体的长是(5×2)分米,宽和高都是5分米;根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】长方体的长是:5×2=10(分米)长方体的宽是5分米,高是5分米;长方体的表面积:(10×5+10×5+5×5)×2=(50+50+25)×2=125×2=250(平方分米)拼成的长方体的表面积是250平方分米。
【点睛】本题考查正方体、长方体的拼接以及长方体的表面积公式的运用,也可以根据拼成的长方体的表面积比原来2个正方体的表面积少2个正方形的面积进行解答。
2019-2020学年度数学五年级下[表面积的变化]沪教版课后练习[含答案解析]五十第1题【单选题】如右图,墙角堆放一些棱长10厘米的正方体,露在外面的面的面积是( )厘米^2 .A、100B、1000C、90D、900【答案】:【解析】:第2题【单选题】一个立方体笔筒,棱长总和为144厘米,它的表面积是( )平方厘米。
A、720B、864C、1728【答案】:【解析】:第3题【判断题】一个长3厘米、宽与高都是2厘米的长方体.将它的前面挖掉一个棱长为1厘米的小正方体,它的表面积比原来大.______(判断对错)A、正确B、错误【答案】:【解析】:第4题【判断题】判断对错正方体的棱长扩大2倍,它的表面积扩大6倍.A、正确B、错误【答案】:【解析】:第5题【填空题】下图是校运动会的领奖台示意图,它是由6各棱长为4分米的正方体组成的,有______个面露在外面,露在外面的面积是______平方分米。
【答案】:【解析】:第6题【填空题】一个长方体它的所有棱长之和为4.8m,它的长、宽、高的比是3:2:1。
现在把这个长方体截成两个小长方体,表面积最多可增加______m^2。
【答案】:【解析】:第7题【填空题】一个长方体的长为7厘米、宽为4厘米、高为2厘米,它的体积是______,表面积是______。
【答案】:【解析】:第8题【填空题】一个长方体木块的长、宽、高分别是5厘米、4厘米、3厘米.如果用它锯成一个最大的正方体,正方体表面积比原来长方体表面积减少______(百分号前保留一位小数)【答案】:【解析】:第9题【填空题】下图是一个长方体。
面的个数+顶点的个数-______=棱的条数。
它的表面积是______平方厘米。
【答案】:【解析】:第10题【填空题】一个圆柱形状的花瓶,底面半径8厘米,高25厘米.这个花瓶的外包装盒是一个长方体,做这样一个包装盒,至少需要______平方厘米的硬纸?【答案】:【解析】:第11题【解答题】包装一个棱长是10cm的正方体礼品盒,实际用纸是表面积的1.2倍,包装好这个礼品盒实际用纸多少平方分米?这个礼品盒的体积是多少立方厘米?【答案】:【解析】:第12题【解答题】一个长方体从正面看如图(1)所示,从上面看如图(2)所示.求该长方体的表面积.A、解:(5×5+5×6+5×6)×2 =(25+30+30)×2=85×2=170(平方厘米)答:长方体的表面积是170平方厘米.【答案】:【解析】:第13题【应用题】一个长方体的长是12厘米,宽8厘米,高是6厘米,它的表面积是多少平方厘米?【答案】:【解析】:。
课题:表面积的变化热身练习(1)将2个棱长为1厘米的小正方体,拼成一个长方体,拼成后的长方体的表面积比原来2个单独的小正方体的表面积减少了 2 个正方形的面积;(2)将5个棱长为1厘米的小正方体,拼成一个长方体,拼成后的长方体的表面积比原来5个单独的小正方体的表面积减少了8个正方形的面积;(3)将棱长为2厘米的3个小正方体拼成一个长方体,拼成后的长方体表面积比原来3个小正方体的表面积之和减少了16 平方厘米;知识精要(1)多个小正方体拼成长方体表面积的变化★把长方体或正方体切成两个或几个长方体(正方体),每切一下会增加2个切面的面积。
反之,把几个长方体或正方体拼成一个长方体,每拼一下会减少2个面的面积。
以此类推得到,增加(或减少)的表面积与切(或拼)的次数n有关,为n×2个拼切面的面积★如何使包装最小几个相同长方体包装在一起,要想使包装纸最节约,就要使最大的面叠加在一起,只有这样,露在外面的面即包装后的表面积最小,包装最节约精解名题【例1】把5个完全一样的正方体拼成一个长方体,长方体的表面积是198平方厘米,求原来一个正方体的表面积?解:54平方厘米【例2】一个长方体长5厘米、宽2厘米、高4厘米,把这个长方体截成大小相等的两个小长方体,两个小长方体的表面积之和比原来这个长方体的表面积增加多少平方厘米?解:3种情况:2×5×2 2×5×4 2×2×4【例3】将3盒长20厘米,宽15厘米,高5厘米的巧克力装成一包,怎样包才能节约包装纸?(接口处不计)需要多少平方厘米的包装纸?解:垒成一个长20厘米,宽15厘米,高5×3=15厘米的大长方体直接运用表面积公式计算包装纸的面积:2×(20×15+20×15+15×15)(2)长、宽、高的变化所引起表面积的变化★若长方体或正方体的高增加(或减少),那么表面积增加(或减少)的大小=长和宽所形成的底面的周长×高增加的数量。
精选2019-2020年沪教版数学五年级下第五单元表面积的变化练习题六十七第1题【单选题】把棱长为6厘米的两个正方体拼成一个长方体,表面积减少( )平方厘米.A、72B、36C、108D、18【答案】:【解析】:第2题【单选题】如右图,墙角堆放一些棱长10厘米的正方体,露在外面的面的面积是( )厘米^2 .A、100B、1000C、90D、900【答案】:【解析】:第3题【单选题】一块长方体木料的横截面是8cm^2 ,把它切成3段(见图),表面积增加( )?A、8cm^2B、16cm^2C、24cm^2D、32cm^2【答案】:【解析】:第4题【判断题】体积相同的两个长方体,它们的表面积一定也相同。
( )A、正确B、错误【答案】:【解析】:第5题【判断题】把一个正方体锯成2个相同的长方体,它的表面积增加了6平方厘米,原来正方体的表面积是36平方厘米。
A、正确B、错误【答案】:【解析】:第6题【填空题】将两个棱长3厘米的正方体拼一个长方体,拼成的长方体的表面积是______平方厘米?体积是______立方厘米?【答案】:【解析】:第7题【填空题】一个长方体前面、上面和左面三个面的面积分别是15平方厘米、10平方厘米、6平方厘米。
这个长方体的表面积是______平方厘米,体积是______立方厘米。
【答案】:【解析】:第8题【填空题】一个正方体的棱长总和是48厘米,它的表面积是______平方厘米,体积是______立方厘米.【答案】:【解析】:第9题【填空题】一个正方体棱长总和是240厘米,这个正方体的表面积是______,体积是______。
【答案】:【解析】:第10题【填空题】一个长方体的金鱼缸,长是8分米,宽是5分米,高是6分米,制作这个鱼缸至少需要玻璃______平方分米.A、196【答案】:【解析】:第11题【填空题】一个正方体表面积是294平方厘米,两个这样的正方体竖直拼合成______,放在地上外露面积是______平方厘米。
【精品】课题:表面积的变化热身练习(1)将2个棱长为1厘米的小正方体,拼成一个长方体,拼成后的长方体的表面积比原来2个单独的小正方体的表面积减少了 2 个正方形的面积;(2)将5个棱长为1厘米的小正方体,拼成一个长方体,拼成后的长方体的表面积比原来5个单独的小正方体的表面积减少了8个正方形的面积;(3)将棱长为2厘米的3个小正方体拼成一个长方体,拼成后的长方体表面积比原来3个小正方体的表面积之和减少了16 平方厘米;知识精要★把长方体或正方体切成两个或几个长方体(正方体),每切一下会增加2个切面的面积。
反之,把几个长方体或正方体拼成一个长方体,每拼一下会减少2个面的面积。
以此类推得到,增加(或减少)的表面积与切(或拼)的次数n有关,为n×2个拼切面的面积★如何使包装最小几个相同长方体包装在一起,要想使包装纸最节约,就要使最大的面叠加在一起,只有这样,露在外面的面即包装后的表面积最小,包装最节约精解名题【例1】把5个完全一样的正方体拼成一个长方体,长方体的表面积是198平方厘米,求原来一个正方体的表面积?解:54平方厘米【例2】一个长方体长5厘米、宽2厘米、高4厘米,把这个长方体截成大小相等的两个小长方体,两个小长方体的表面积之和比原来这个长方体的表面积增加多少平方厘米?解:3种情况:2×5×2 2×5×4 2×2×4【例3】将3盒长20厘米,宽15厘米,高5厘米的巧克力装成一包,怎样包才能节约包装纸?(接口处不计)需要多少平方厘米的包装纸?解:垒成一个长20厘米,宽15厘米,高5×3=15厘米的大长方体直接运用表面积公式计算包装纸的面积:2×(20×15+20×15+15×15)★若长方体或正方体的高增加(或减少),那么表面积增加(或减少)的大小=长和宽所形成的底面的周长×高增加的数量。