沪教版数学五年级下知识点

五上Module 1 -Getting to know each other 教学目标：1.学会在具体语境中使用新单词。

2学会用want+动词不定式用法。

3.学会介词on，by ，at的某些用法。

4.学会疑问代词what，how, when的用法5.学会序数词的写法和读法。

重点词汇：① job taxi driver cook pilot teach teacher become②by walk Ms un dergr ound after hour③party whe n beg in bring thing favouritein teresti ng重点句型：1. -What do you want to be ？-I want to be a pilot.2.-How do you come to school?-I come to school on foot.3. -When' s your birthday?-It ' s on 26 th September语音发音：sk sp stModule 2 -Relationship教学目标：1.学会在具体语境中使用新单词。

2掌握一般现在时的常用频度副词。

3..学会用所学词汇句型介绍朋友。

4.学会用现在进行时be+v ing 用法。

5.学会形容词性物主代词my our your their 的用法重点词汇：① 频度副词usually often sometimes always n ever② clever same differe nt both heavy easy say an swer③房间livi ng room bedroom kitche n bathroom重点句型：1. -What do you usually do with your gran dpare nts?-I usually play chess with my gran dpare nts.2.Kitty likes... Alice likes... we bothlike...3.-Where are you?-I'm in the bathroom. I ' m doing my homework. 语音发音：sh dr pr br crModule 3 -Out and about教学目1.学会在具体语境中使用新单词。

沪教版数学五年级下知识点(1)自然数: 0，1，2，3，…这些用来计数、编排次序、编码的数被称为自然数。

(2)没有最大的自然数。

每个自然数n都接着后一个自然数" n+1 "。

自然数这样一直延续下去,永无止境。

(3)自然数可以表示个数、序数、量数。

(4)0是自然数。

(5)毎一个自然数都只有一个自然数紧接在它的后面。

自然数n的后一个自然数是“n+1"。

(6)最小的自然数是0,没有最大的自然数。

正负数(1)前面有“+”号的数都是正数;前面有“-"号的数都是负数;零既不是正数也不是负数。

(2) 正数前面的“+”可以省略不写。

（3）零既不是正数也不是负数。

数轴为了表示负数,我们从数射线上的“0"点出发,向相反方向(左)延长,使它成为一条直线,这样的直线就成为了数轴。

数轴的画法:(1)画一条直线（一般画水平位置的直线),在直线上任取一点表示零,把这点叫做原点。

(2)规定一个方向（一般取从左往右的方向）为正方向,用箭尖表示,那么相反方向就是负方向。

(3)再选取适当的长度作内一个单位长度,直线上从原点向右,毎隔一个単位长度取一个点,依次表示1，2，3，…从原点向左,用类似方法依次取点表示-1 -2, -3, …我们把规定了原点、正方向、单位长度的一条直线叫做数抽。

用数轴上的点表示数,所有表示正数的点都在原点的右边，所有表示负数的点都在原点的左边。

原点(表示0的点)是表示正数和负数的点的分界点。

正数都大于0,负数都小于0，正数大于负数。

简易方程先找等量关系，再列式解答和倍问题:已知两个数的和与两个数的倍数关系，求两个数各是多少的应用题。

差倍问题:已知两个数的和与两个数的倍数关系，求两个数各是多少的应用题。

和差问题:已知两数的和及它们的差，求这两个数各是多少的应用题。

行程问题:两个物体/人相对而行，在途中相遇。

追及问题:两个物体/人同一起点，慢的先走，然后快的追慢的;两个物体/人不同地点，同时出发，快的追慢的，最后相遇。

沪教版小学五年级数学下册知识点梳理一、数的认识在小学五年级数学下册中，学生需要掌握的第一个知识点是数的认识。

具体来说，这个知识点要求学生了解数的种类，认识正数和负数，以及学会进行简单的数的比较。

在此基础上，学生需要进一步了解相反数和绝对值的概念，能够进行相应的计算。

二、小数的认识小数是小学五年级数学下册中的另一个重要知识点。

学生需要明确小数是一种有限的分数，能够进行小数的简单变形运算，并学会进行小数之间的比较。

此外，学生还需要了解十进制的概念，知道如何用十进制表示小数。

三、分数的认识与小数类似，分数也是小学五年级数学下册的一项重要内容。

学生需要了解分数的基本概念，如分子、分母、完全分数、假分数等。

此外，学生还需要掌握分数间的四则运算，包括加法、减法、乘法、除法等。

四、面积与周长小学五年级数学下册中的面积与周长也是不可或缺的知识点。

学生需要了解如何计算简单图形的面积和周长，掌握正方形、长方形和三角形等基本图形的面积和周长计算方法。

同时，学生还需要了解圆的概念和计算方法。

五、时、分和秒的认识在小学五年级数学下册中，学生需要掌握时、分和秒的概念和计算方法。

具体来说，学生需要学会用时、分和秒来表示时间，能够将时间进行转化和换算，掌握简单的时间计算方法。

六、三角形与四边形小学五年级数学下册中的三角形与四边形是其中比较重要的知识点。

学生需要了解三角形和四边形的基本属性，掌握相应的计算方法。

同时，学生还需要学会绘制和分析简单的三角形和四边形，能够进行简单的判断和计算。

七、数据的收集与整理数据的收集与整理也是小学五年级数学下册的主要内容之一。

学生需要了解如何进行数据的收集和整理，掌握数据的表示方法和分析方法。

同时，学生还需要学会用图表的形式来表示数据，并进行简单的数据分析。

八、几何体的认识在小学五年级数学下册中，学生需要掌握几何体的概念和分类，并了解它们的特点和性质。

具体来说，学生需要学会描述几何体的形状和大小，并掌握求解几何体的表面积和体积的方法。

沪教版数学五年级下册知识点总结数学起源于人类早期的生产活动，古巴比伦人从远古时代开始已经积累了一定的数学知识，并能应用实际问题。

下面是整理的沪教版数学五年级下册知识点，仅供参考希望能够帮助到大家。

沪教版数学五年级下册知识点1.轴对称：如果一个图形沿一条直线折叠，直线两侧的图形能够互相重合，这个图形就叫做轴对称图形，这时，我们也说这个图形关于这条直线(成轴)对称。

对称轴：折痕所在的这条直线叫做对称轴。

2.轴对称图形的性质：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点。

轴对称和轴对称图形的特性是相同的，对应点到对称轴的距离都是相等的。

3.轴对称的性质：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

这样我们就得到了以下性质：(1)如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

(2)类似地，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

(3)线段的垂直平分线上的点与这条线段的两个端点的距离相等。

(4)对称轴是到线段两端距离相等的点的集合。

4.轴对称图形的作用：(1)可以通过对称轴的一边从而画出另一边;(2)可以通过画对称轴得出的两个图形全等。

5.因数：整数B能整除整数A，A叫作B的倍数，B就叫做A 的因数或约数。

在自然数的范围内例：在算式6÷2=3中，2、3就是6的因数。

6.自然数的因数(举例)：6的因数有：1和6，2和3.10的因数有：1和10，2和5.15的因数有：1和15，3和5.25的因数有：1和25，5.7.因数的分类：除法里，如果被除数除以除数，所得的商都是自然数而没有余数，就说被除数是除数的倍数，除数和商是被除数的因数。

我们将一个合数分成几个质数相乘的形式，这样的几个质数叫做这个合数的质因数。

8.倍数：对于整数m，能被n整除(n/m)，那么m就是n的倍数。

沪教版五年级数学的复习提纲第二单元小数乘除法1、小数乘整数：意义——求几个相同加数的和的简便运算。

如：1.5×3表示1.5的3倍是多少或3个1.5的和的简便运算。

计算方法：先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

2、小数乘小数：意义——就是求这个数的几分之几是多少。

如：1.5×0.8就是求1.5的十分之八是多少。

1.5×1.8就是求1.5的1.8倍是多少。

计算方法：先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

注意：计算结果中，小数部分末尾的0要去掉，把小数化简;小数部分位数不够时，要用0占位。

3、规律：一个数0除外乘大于1的数，积大于原来的数;一个数0除外乘等于1的数，积等于原来的数。

特值法代入一个数0除外乘小于1的数，积小于原来的数。

4、求近似数的方法：⑴四舍五入法;⑵进一法;⑶去尾法5、计算钱数，保留两位小数，表示计算到分。

保留一位小数，表示计算到角。

6、小数四则运算顺序跟整数是一样的。

7、运算定律和性质：加法：加法交换律：a+b=b+a 加法结合律:a+b+c=a+b+c减法：减法性质：a-b-c=a-b+c a-b-c=a-b+c乘法：乘法交换律：a×b=b×a 乘法结合律：a×b×c=a×b×c乘法分配律：a+b×c=a×c+b×c 【a-b×c=a×c-b×c】重点强调除法：除法性质：a÷b÷c=a÷b×c8、小数除法的意义：已知两个因数的积与其中的一个因数，求另一个因数的运算。

如：0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3，求另一个因数的运算。

组合体的体积【知识要点】 1、长方体的体积公式长方体的体积＝长×宽×高，如果用a b h 、、分别表示长方体的长、宽、高，V 表示体积，那么=V abh 。

2、正方体的体积公式正方体的体积＝棱长×棱长×棱长，用字母表示为3V a a a a =⋅⋅=。

3、组合图形的体积求组合图形体积的一般方法：先把组合图形合理的切割成几个长方体与正方体，然后分别计算体积后再相加。

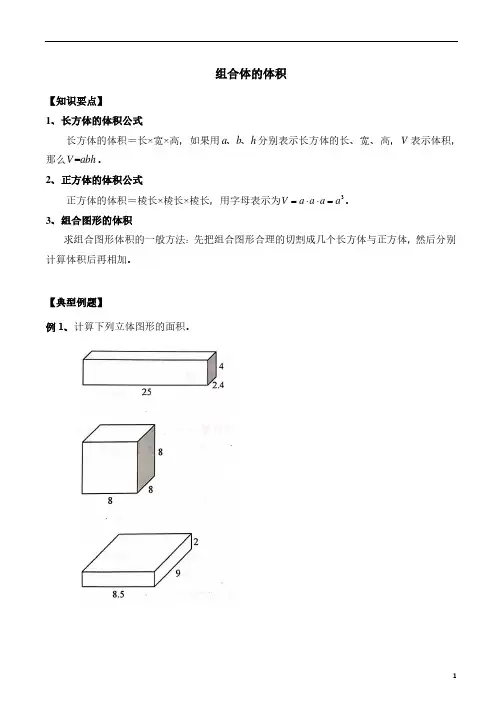
【典型例题】例1、计算下列立体图形的面积。

例2、计算下列零件的体积。

（单位：分米）随堂练：计算下列组合体的体积。

（单位：厘米）例3、判断题。

（1）长方体的长是8分米,宽是6分米,高是5厘米,体积是240立方分米。

（）（2）甲、乙两个长方体,它们长、宽、高的和相等,则它们的体积也一定相等。

（）（3）一个正方体,如果把它的棱长增加1分米,那么体积增加1立方分米。

（）（4）把4个棱长是5厘米的正方体,拼成一个长方体,这个长方体的体积是0.5立方分米。

（）例4、选择题（1）一个长方体的体积是360立方厘米,宽是9厘米,高是4厘米,关于长方体的长,下列选项中不正确的是（）。

（A）10厘米（B）1分米（C）0.1米（D）1000毫米（2）一个长方体的体积是64立方分米,下面长、宽、高中不可能的是（）。

（A）8分米,4分米,2分米（B）4分米,4分米,4分米（C）16分米,2分米,2分米（D）6分米,4分米,3分米应用题讲解：1、一个正方体，它的长、宽、高分别是5厘米，4厘米，2厘米，如果长、宽、高各增加1厘米，那么体积就要增加多少立方厘米？2、一块长方体木块，长是10厘米，宽是8厘米，高是6厘米，先从长方体木块上切下一块尽可能大的正方体，接着再从剩下的立体图形中切下一个尽可能大的正方体，问：现在剩下立体图形的体积是多少立方厘米？3、一个正方体，棱长是2厘米，如果棱长增加2厘米，那么体积就要增加多少立方厘米？4、如图，把一个大长方体木块切成一个小长方体和一个大正方体，已知小长方体的体积是60立方厘米，长是2.4厘米，求大长方体的体积。

代数与方程的复习课时目标1、理解用字母表示数的意义，并会用含有字母的式子表示数量关系。

2、熟练掌握含有字母的乘式及乘方的简便写法，会代入求值。

3、理解、掌握并会区别方程、方程的解、解方程三个概念。

4、熟练掌握解方程与列方程解文字题的格式，方法，步骤。

知识精要1．用字母表示数用字母表示数是代数的一个重要特点，它包括：数量关系、运算定律、计算公式等。

要注意的是：在含有字母的式子里，数字与字母、字母与字母之间可以省略乘号；数字与字母相乘时，要把数字放在字母前面；当1与任何字母相乘时，1省略不写。

用字母表示数不仅把数量关系简明地表达出来，也把运算的结果表示出来。

2．列代数式①代数式：用运算符号（加减乘除以及后面的乘方、开方）把数及表示数的字母连接起来的式子称为代数式。

②列代数式的关键：正确理解数量关系，弄清运算顺序和括号的使用。

③代数式的值：用数值代替代数式里的字母，按照代数式指明的运算，计算出的结果，就叫代数式的值。

（注：代数式的值是个具体的量，这个量随字母的取值不同按给定的运算顺序会计算出不同的数量。

求代数式的值时，要注意代数式里的字母所取值不能使代数式或代数式所表示的实际数量关系无意义。

）3.等式的概念：表示等号两边相等量的式子。

等式的性质：在等式两边同时加上或同时减去一个相同的数等号不变；在等式两边同时乘以或同时乘以一个不为零的数，等号不变。

4.方程的概念：含未知数的等式叫做方程；把等式一边的某项变号后移动到另一边，叫做移项。

使方程左右两边相等的未知数的值就叫做方程的解。

解一元一次方程的一般步骤，先移项，后合并，再求解。

5.列方程解应用题：①读题，理解题意，找出等量关系；②设未知量，根据所找的等量关系列方程；③检验。

④写答句。

热身练习一、用含有字母的式子表示下面的数量关系：1、比x的四分之一少3的数是x÷4-3 。

2、M与3的和的五倍减去6是5（M+3）-6 。

3、学校去年植树a棵，今年植树的棵数比去年的2倍还多6棵，今年植树（2a+6）棵。