同底数幂相乘

同底数幂的乘法化简在数学中，同底数幂的乘法是一种常见的运算，它可以帮助我们简化复杂的指数表达式。

同底数幂的乘法指的是两个或多个指数的底数相同，通过乘法运算将它们合并成一个简化的指数表达式。

这种运算在代数表达式简化、解决实际问题等方面都具有重要的应用价值。

首先，让我们来看一个简单的例子，假设有两个同底数幂相乘，即a^m a^n。

根据指数的乘法法则，我们知道当底数相同时，指数相加。

因此，a^m a^n = a^(m+n)。

这就是同底数幂的乘法化简的基本原理。

接下来，让我们通过一个具体的例子来演示同底数幂的乘法化简。

假设我们要化简表达式，2^3 2^5。

根据指数的乘法法则，我们可以将底数为2的指数相加，即2^(3+5) = 2^8。

因此，原表达式可以化简为2^8。

同底数幂的乘法化简不仅适用于两个指数相乘的情况，它也可以推广到多个指数相乘的情况。

例如，假设有三个同底数幂相乘，a^m a^n a^p。

根据指数的乘法法则，我们可以将它们合并为一个指数表达式，即a^(m+n+p)。

在实际问题中，同底数幂的乘法化简也具有重要的应用。

例如，在计算复杂的代数表达式时，我们经常需要将同底数幂相乘进行化简，以便更清晰地理解和计算表达式。

此外，它还可以帮助我们简化指数函数、解决指数方程等问题。

总之，同底数幂的乘法化简是代数中的基本运算之一，它通过合并同底数幂的指数，帮助我们简化复杂的指数表达式，具有重要的理论和实际应用价值。

掌握了同底数幂的乘法化简，我们可以更加灵活地运用指数的性质，解决各种数学问题。

同底数幂的乘法与除法幂运算是数学中常见的运算方式之一，它可以用来表示数字的指数形式。

当底数相同时，我们可以进行同底数幂的乘法和除法运算。

本文将介绍同底数幂的乘法和除法规则，以及它们的应用。

一、同底数幂的乘法规则当底数相同时，两个幂相乘的结果可以通过将指数相加来得到。

具体表达式如下：a^m * a^n = a^(m+n)其中，a表示底数，m、n为指数。

例如，如果我们要计算2的3次方乘以2的5次方的结果，可以使用同底数幂的乘法规则来计算：2^3 * 2^5 = 2^(3+5) = 2^8 = 256同样地，我们可以推广到更多个同底数幂相乘的情况。

例如：3^2 * 3^4 * 3^6 = 3^(2+4+6) = 3^12这个规则在计算中非常有用，可以简化复杂的幂运算。

二、同底数幂的除法规则当底数相同时，两个幂相除的结果可以通过将指数相减来得到。

具体表达式如下：a^m / a^n = a^(m-n)仍然以2为底数为例，计算2的7次方除以2的4次方的结果：2^7 / 2^4 = 2^(7-4) = 2^3 = 8同样地，我们可以推广到更多个同底数幂相除的情况。

例如：5^8 / 5^3 / 5^5 = 5^(8-3-5) = 5^0 = 1这个规则可以帮助我们在幂运算中进行除法运算，避免了繁琐的计算步骤。

三、应用举例同底数幂的乘法和除法规则在实际问题中有广泛的应用。

以下是一些例子：例1：计算房子的总面积如果一座房子的长为10米，宽为5米，高为3米，我们可以使用同底数幂的乘法规则来计算房子的总面积。

房子的总面积等于侧面积与顶面积之和。

假设侧面积用S表示，顶面积用A表示，则总面积为：S + 2A = (10*3 + 5*3)*2 = 90 + 30 = 120 平方米例2：计算国内生产总值国内生产总值（GDP）是衡量一个国家经济总量的指标。

我们可以使用同底数幂的乘法规则来计算GDP。

假设国家的人均GDP为每年5%的增长率，而人口数量每年以每年1%的增长率增加。

一、概念与法则：1、同底数幂的乘法：同底数幂乘法的运算法则：同底数幂相乘，底数不变，指数相加。

即：am﹒a n =a m+n （m 、n 均为正整数）例题1： x 2·x 5 = 2×24×23 = x m ·x 3m+1= （a+1）·（a+1）6= 2、幂的乘方：幂的乘方运算法则：幂的乘方，底数不变，指数相乘。

即：（am）n =a mn （m 、n 均为正整数）例题2：计算（1）（103）3 = （2）[（32）3]4 =（3）[（－6）3]4= （4）（x 2）5= －[（a —1）2]7 = （6）（－a s ）3= （7）（x 3）4·x 2 = （9）[（x 2）3]7 = 3、积的乘方：积的乘方，等于把积中的每个因式分别乘方，然后把所得的幂相乘。

即（ab ）n=a n b n （m 、n 均为正整数）例题3、计算：（1）（2a ）3= （2）（-5b ）3= （3）（xy 2）2= （4）（-2x 3）4=注意：①、积的乘方是指底数是乘积形式的乘方。

②、此法则也可以逆用，即：a n b n =（ab ）n。

4、同底数幂的除法：同底数幂的除法法则：同底数幂相除，底数不变，指数相减， 即：am÷a n =a m-n （a ≠0； m 、n 均为正整数）例题4.计算52()()x x -÷-=_______,10234x x x x ÷÷÷ =______.5、特别规定零指数幂：零指数幂的意义：任何不等于0的数的0次幂都等于1 即：a=1（a ≠0）6、负指数幂：任何不等于零的数的―p 次幂，等于这个数的p 次幂的倒数，即：1(0)p p a a a -=≠例题5：⑴.若0(2)x -有意义,则x_________； ⑵.02(3)(0.2)π--+-=________.二、典型例题：例1：. 化简（1）、 (x-y)2(x-y)3(y-x)2(y-x)3 （2）210.52x x y x y x x x x y ⋅⋅⋅-⋅⋅+⋅⋅例2、⑴若2m =4，2n =8，求2m+n ，22m+3n 的值． ⑵若a 2n =3，求（a 3n ）4的值。

同底数幂的乘法公式：同底数幂相乘，底数不变，指数相加： a^m×a^n=a^(m+n)）（m 、n 都是正整数） 同底数幂的除法同底数幂相除，底数不变，指数相减： a^m÷a^n=a^(m -n)（m 、n 都是整数且a≠0）。

负实数指数幂的一般形式是a^(-p) =1/(a) ^p 或（1/a ）^p (a≠0，p 为正实数）零指数幂： 单项式与多项式的乘法公式：a ×(a+b)=a ×a+a ×b多项式与多项式的乘法公式：（a+b ）(c+d)=ac+ad+bc+bd扩展：（a+b+c ）(d+e+f)=ad+ae+af+bd+be+bf+cd+ce+cf练习题:同底数幂的乘法一、知识点检测1、同底数幂相乘，底数 ，指数 ，用公式表示=n m a a（m ，n 都是正整数）2、计算32)(x x ⋅-所得的结果是（ ）A.5xB.5x -C.6xD.6x -3、下列计算正确的是（ ）)0(10≠=a aA.822b b b =⨯B.642x x x =+C.933a a a =⨯D.98a a a =4、计算：（1）=⨯461010 （2）=⎪⎭⎫ ⎝⎛-⨯-6231)31( （3）=⋅⋅b b b 32 （4）2y ⋅ 5y =5、若53=a ，63=b ，求b a +3的值同底数幂的除法1.a m ÷a n =_____,此式成立的条件是_____.2.412÷43=_____;x 11÷x 6=_____.3.(－a )5÷(－a )=_____;(－xy )7÷(－xy )2=_____;32m +1÷3m －1=_____.4.用科学记数法表示：－0.0000425=_____;3560000=_____.5.(abc )4÷(abc )=_____,(x +1)m －1÷(x +1)·(x +1)3=_____.6.若a m +2÷a 3=a 5,则m =_____；若a x =5,a y =3,由a y －x =_____.7.x 8÷_____=x 5÷_____=x 2;a 3÷a ·a －1=_____.8.(a －2b )3·(a －2b )4÷(a －2b )69.(－x 5)÷(－x )3·(－x )10.x ·(－x )2m +1÷(－x 4m －1)负实数指数幂与零指数幂1、（-3）-32、2)3(1--3、2)32(--4、（23-1）-35、a 5·a 2÷a 66、若（x-3）0-2（3x-6）-2有意义，那么x 的取值范围 7若式子有意义，则x 的取值范围为 多项式的乘法试题 1．计算： （1）（a+2b ）（a-b ）=_________；（2）（3a-2）（2a+5）=________； （3）（x-3）（3x-4）=_________；（4）（3x-y ）（x+2y ）=________．2．计算：（1）(x －8y )( x －y ) （2） (x －1)(－2x －3) （3）(m －2n )(3m ＋n )0(21)x-（4）(x －2)(x ＋2) （5）(x －y ) (x 2＋xy ＋y 2) （6）n (n ＋1)(n ＋2)（7）()()m n m n +-+ （8）22)2(x y x -- （9） (32)(32)a a ---（10）（a+b+2）(a+b-2) (11))168()4(2--+x x (12) 22(1)(1)mn mn +--（13）xy －（x －1）（x + 1） （14）2(2)4()(2)x y x y x y ---+（15）5(x －1)(x+3)－2(x －5)(x －2) （16）2)23()3)(12(---+x x x。

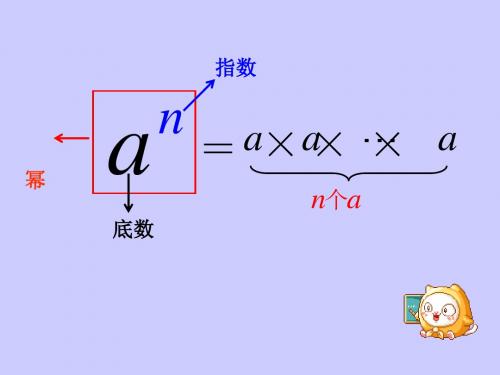
8.1 幂的运算1.同底数幂的乘法知识点一 同底数幂的意义及其乘法的运算性质1. 同底数幂的意义同底数幂是指底数相同的幂。

如5322与底数同为2；2)2()275---底数同为与（；b a b a b a 27232)()(底数同为与；y x y x y x ---底数同为与32)()(。

2. 同底数幂的乘法的运算性质（幂的运算性质1）同底数幂相乘，底数不变，指数相加。

用字母表示为n m n m aa a +=•（m ，n 都是正整数）例1 计算（1）a a a ••25 （2）67)()(a a -•- （3）32a a •- （4）32)(a a •-例2 计算：52)2()2(x y y x -•-知识点二 同底数幂的乘法的运算性质的逆用逆用法则：n m n m a a a•=+（m ，n 都是正整数）。

如3352462222222⨯=⨯=⨯=。

在计算中根据题目的具体特点灵活处理。

例3 （1）已知===+b a b a 373,53，则 。

（2）==2018201633，则m （用含m 的代数式表示）典型例题剖析题型一 同底数幂的乘法1.同底数幂的乘法的运算性质的应用例1 计算：（1）x x x •-•33)( （2）523)()(a a a -••-（3）2017453)()()()(a b a b b a b a -•-•-•-2.同底数幂的乘法的运算性质的实际应用例2 宇宙中的距离是以光年作为单位，1光年是指光在1年内通过的距离。

如果光的速度为s km /1035⨯，1年约为s 7102.3⨯，那么1光年约是多少千米？3.同底数幂的乘法与整式加减的综合例3 计算：4353x x x x x ••+•例4 下列计算结果正确的是（ ）A. 9432)21()21()21()21(21-=-⨯-⨯-⨯- B.632)()()()(b a a b a b b a --=--- C.6363642)2()2(=-+- D.211+++=+n n n x x x4.同底数幂的乘法的运算性质与方程的综合例5 已知a23223=⨯，则关于x 的方程)1(26-=+a ax 的解是例6 如果y x ，为自然数，且822=⨯y x ，试确定x ，y 的值。

同底数幂的运算是数学中一个重要的概念，它涉及到幂和指数的计算。

下面介绍它的定义和运算规则。

定义：同底数幂运算是指用同一个底数的幂进行计算，也叫指数运算。

比如，底数为a，指数为m、n，则有am•an=a(m+n)。

运算规则：
（1）乘幂运算：如果底数相同，指数相加，即am•an=a(m+n)。

（2）除幂运算：如果底数相同，指数相减，即am/an=a(m-n)。

（3）指数运算：如果底数相同，指数相乘，即(am)n=a(mn)。

（4）幂的乘方运算：如果底数相同，指数相乘，即(am)n=a(m+n)。

（5）幂的平方运算：如果底数相同，指数平方，即(am)2=a(m2)。

上面介绍了同底数幂的定义和运算规则，它是数学中的一个重要概念，在学习和使用数学的过程中必不可少。

正确理解和运用同底数幂运算，能让我们在数学学习和应用中取得更大的成功。