- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本要求:变换后定限简便,求积容易. 基本要求:变换后定限简便,求积容易.
∂( x, y) 1 2. J = . = ∂(u,v) ∂(u,v) ∂( x, y)
二、例题分析
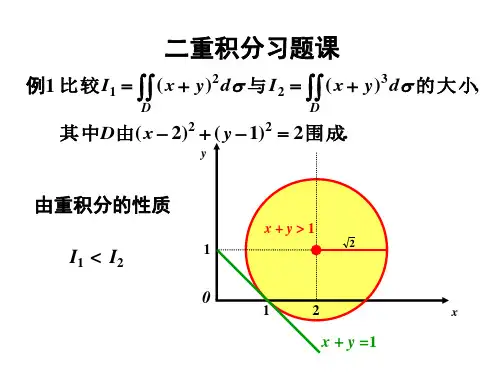
(x2 + y2 )dσ D: 2x − x2 ≤ y ≤ 4− x2 例1 计算 ∫∫
D
解
积分区域由不等式给出 在不等式中取等号所得的曲线是两个半圆 但它们围不成区域 要使 2 x − x , 4 − x 都有意义 必须限制 x ∈ [0,2]
∫ f (r)rdr 0
4
D1 D
π
⇒ I = 4∫ dr ∫ rf (r )dθ + 4 ∫ dr
0
1
1
π
2
0
2
1
1 = π ∫ rf ( r )dr + ∫ (π − 4 arccos )rf ( r )dr r 0 1
arccos r
∫ rf (r )dθ 1
4
1 = π ∫ rf (r )dr − 4 ∫ rf (r ) arccos dr r 0 1
2
2
注
依题意, 依题意,要化为定积分首先应设法将二元函数 f ( x 2 + y 2 ) 化为一元函数 自然想到用极坐标 其次, 其次,若先对 r 后对 θ 不可进一步化为定积分 又想到换序 例8 连续, 设 f(x) 连续,证明
A
A A ∫∫ f (x − y)dxdy = −∫Af (t)[A− | t |]dt D:| x |≤ 2 ,| y |≤ 2 D
证一 令 u = x − y, v = x + y 则
v + u = 2x, v − u = 2 y
D → D′ : − A ≤ u + v ≤ A,− A ≤ v − u ≤ A ∂( x, y) 1 J= = ≠0 ∂ ( u, v ) 2
化累次积分后 外限是常数 内限是外层积分变量的函数或常数 极坐标系下勿忘
r
4。关于对称性 。
利用对称性来简化重积分的计算是十分有效的, 利用对称性来简化重积分的计算是十分有效的, 它与利用奇偶性来简化定积分的计算是一样的, 它与利用奇偶性来简化定积分的计算是一样的,不 过重积分的情况比较复杂,在运用对称性是要兼顾 过重积分的情况比较复杂,在运用对称性是要兼顾 被积分函数和积分区域两个方面, 被积分函数和积分区域两个方面,不可误用 对 I = f ( x , y )dxdy ∫∫ ①若D关于 x 轴对称 关于
D D
D2 D1
xyf ( x2 + y2 )dσ = 0 ∫∫
D
0
1
∫∫ xdσ = ∫∫ xdσ = ∫ xdx ∫ dy D D
−1 x
3
−x
3
2 =− 5
2 I =− 5
1
例6 设 f (x) 在 [0,1] 上连续
1 1
求
∫ dx∫ f (x) f ( y)dy 0 x
1 1
∫ f (x)dx = A 0
(2)当f (− x, y) = f ( x, y)时 I = 2∫∫ f ( x , y )dxdy
D1 = {( x, y)( x, y) ∈ D, x ≥ 0}
D1
当 (1) f(− x, y) = − f( x, y) I = 0 − 时 (2)当f (− x,− y) = f ( x, y)时 I = 2∫∫ f ( x, y)dxdy
π
0
0
π
2
0
π
= ∫ [sin
0
2
π
2
−x
=π −2
− sin x ]dx − ∫ [cos x − sin ]dx 2 2 0
π
D2 D1
∫∫ sin(x + y) dxdy= 2π D : 0 ≤ x ≤ π ,0 ≤ y ≤ π
D
x+ y =
π
2
( x + y)dxdy, D: x2 + y2 ≤ x + y 例4 计算 ∫∫
确定积分限时一定要保证下限小于上限
定限
看图定限 —穿越法定限 和不等式定限 穿越法定限 先选序, 先选序,后定限
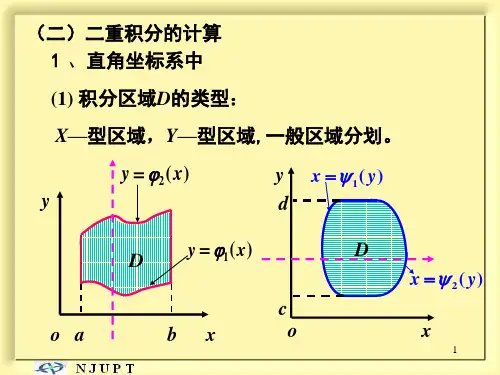
①直角坐标系 ⅰ。先 y 后 x , 过任一x ∈ [ a , b ],作平行于 y 轴的直线 作平行于 穿过D的内部 穿过 的内部 内层积分的下限 从D的下边界曲线 y = ϕ1 ( x) 穿入 —内层积分的下限 的下边界曲线 内层积分的上限 从上边界曲线 y = ϕ2 ( x) 穿出 —内层积分的上限 ⅱ。先 x 后 y 过任一 y ∈[ c , d ] 作平行于 x 轴的直线
关于原点 ③若D关于原点对称 关于原点对称
D3 = {( x, y)∈ D, x ≥ 0, y ≥ 0}
D3
关于直线 ④若 D 关于直线
y=x
对称
∫∫ f ( x, y)dxdy= ∫∫ f ( y, x)dxdy D D
——称为关于积分变量的轮换对称性 称为关于积分变量的轮换对称性 是多元积分所独有的性质 ①、②、③简单地说就是 奇函数关于对称域的积分等于0, 奇函数关于对称域的积分等于 ,偶函数关 于对称域的积分等于对称的部分区域上积分的两 倍,完全类似于 对称区间上奇偶函数的定积分的 性质 简述为“ 对称, 奇偶” 简述为“你对称,我奇偶”
r1 (θ ) ——内下限 内下限 r2 (θ ) 具体可分为三种情况
⑴极点在D的外部 极点在 的外部
—内上限 内上限
α ≤ θ ≤ β , r1 (θ ) ≤ r ≤ r2 (θ ) 极点在D的边界上 ⑵极点在 的边界上 α ≤ θ ≤ β , r1 (θ ) ≤ r ≤ r2 (θ )
α, β 是边界在极点处的切线的极角 r (θ ) 绝大多数情况下为 绝大多数情况下为0 1 极点在D的内部 ⑶极点在 的内部 0 ≤ θ ≤ 2π ,0 ≤ r ≤ r (θ )
2 以原点为起点作射线 这射线和两个半圆相交
从
θ ∈ [ 0, ]
π
r = 2cos θ
穿入
从
r =2
穿出
尽管极点在D的边界上 尽管极点在 的边界上 但极角为 θ (∈ [0, ]) 2 的射线并不是从极点穿入 域D的极坐标表示为 的极坐标表示为 而不是
π
0 ≤θ ≤ π ,0 ≤ r ≤ 2 2 π
1
y
解 I = dx f ( x) f ( y)dy = dy f ( x) f ( y)dx
1 x
∫ ∫ 0 x
x
∫ ∫ 0 0
1
= ∫ dx∫ f ( x) f ( y)dy
1
0
0
1
⇒ 2I = ∫ dx∫ f ( x) f ( y)dy + ∫ dx∫ f ( x) f ( y)dy
0 0 0 x
12 12 1 解 D的边界 ( x − ) + ( y − ) = 的边界 2 2 2
极点在D的边界上 极点在 的边界上 圆周在(0, 的切线斜率为 圆周在 0)的切线斜率为 y′ = −1 π 3π 故 α = − ,β = 4 4 3π
D
I=
−
∫π (cosθ + sinθ )dθ ∫ r dr 0
∂x ∂( x, y) ∂u J (u, v ) = = ∂(u, v ) ∂y ∂u
∂x ∂v ≠ 0 ∂y ∂v
∫∫ f ( x, y)dxdy = ∫∫ f [ x(u, v), y(u, v)]J (u, v)dudv D D
1
注意
1.作什么变换主要取决 于积分区域 D 的形状, 的形状, 同时也兼顾被积函数 f ( x , y ) 的形式. 的形式.
2 2
因此D只能在 因此 只能在x=0 , x=2 之间 确定了积分区域后, 确定了积分区域后,再看被积函数结合积 分区域的特点, 分区域的特点,化成极坐标计算较为简单
显然 r 呢? 0 ≤θ ≤π 2 极点在D的边界上 的边界上, 极点在 的边界上,所以 0 ≤ r ≤ 2 那就错了 积分限如何确定 不能以为极点O在区域的边界上 不能以为极点 在区域的边界上 积分的下限为0 就误以为对 r 积分的下限为 的积分限, 定 r 的积分限,应先固定
D
1
1
1
1
= ∫ dx∫ f ( x) f ( y)dy = ∫ f ( x)dx∫ f ( y)dy
0 0 0 0
A = [∫ f ( x)dx] = A ⇒I = 2 0 f ( 连 例7 设 ( x)在 −∞,+∞)上 续 试将二重积分
2 2
1
2
I = ∫∫ f ( x2 + y2 )dσ
D
4 3π 4 4
4
cosθ + sinθ 2
π 1 4 4 4 = ∫ (cosθ + sinθ ) dθ = ∫ sin (θ + )dθ 3 −π 3 −π 4
4
3π 4
(和差化积) 和差化积)
π 4 4 = ∫ sin tdt = 2 30
D
π
( 令t = θ + ) 4
π
例5 计算 ∫∫ x[1+ yf ( x2 + y2 )]dσ D: y = x3, y = 1, x = −1 解 2 2 I = ∫∫ xdσ + ∫∫ xyf ( x + y )dσ
5 关于二重积分的换元法
f(x,y)在D上连续 变换 : x=x(u,v),y=y(u,v) 在 上连续 变换T: 平面的闭区域D 平面上的闭区域D 将 uov 平面上的闭区域 1 变成 xoy 平面的闭区域
(1) x=x(u,v),y=y(u,v)在D1上具有连续的一阶偏导数 ) 在 (2)在D1上 )