相似三角形中的面积问题

相似三角形的面积关系总结
相似三角形是指具有相同形状但大小不同的三角形。

在研究相
似三角形时，我们可以得出一些有用的面积关系。

1. 面积比例：相似三角形的面积与它们对应边长的平方成正比。

设两个相似三角形的边长比为a:b，则它们的面积比为a²:b²。

2. 高度比例：相似三角形的高度与它们对应边长的比例相等。

设两个相似三角形的边长比为a:b，则它们的高度比为a:b。

3. 面积差比例：如果在一个相似三角形的每条边上分别取等比
例的线段，则这些线段所分割出的新三角形的面积比等于相似三角
形的边长比的平方。

4. 面积和比例：如果一个相似三角形的每条边上分别取等比例
的线段，则这些线段所分割出的新三角形的面积比等于相似三角形
的边长比的平方。

这些面积关系对于解决与相似三角形有关的几何问题非常有用。

我们可以利用它们来计算未知三角形的面积，比较不同三角形的面
积大小，以及推导出其他有用的几何关系。

总结了相似三角形的面积关系，我们能更好地理解三角形的性质，并在解决实际问题时灵活运用。

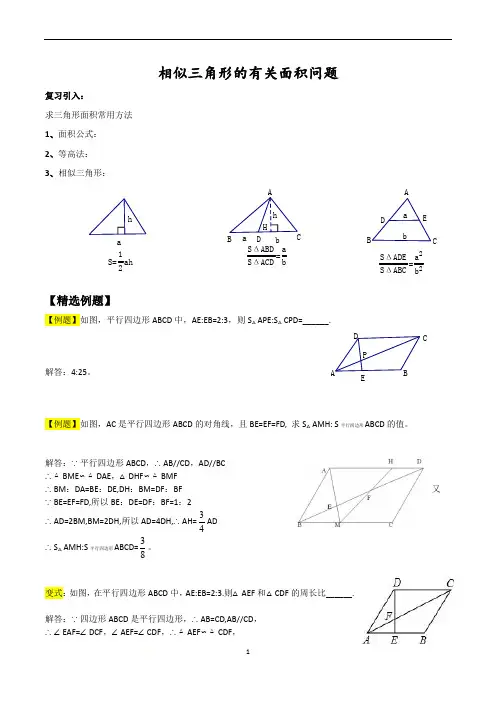
相似三角形的有关面积问题复习引入：求三角形面积常用方法1、面积公式：2、等高法：3、相似三角形：【精选例题】【例题】如图，平行四边形ABCD 中，AE:EB=2:3，则S △APE:S △CPD=______.解答：4:25。

【例题】如图，AC 是平行四边形ABCD 的对角线，且BE=EF=FD, 求S △AMH: S 平行四边形ABCD 的值。

解答：∵平行四边形ABCD ，∴AB//CD ，AD//BC ∴△BME ∽△DAE ，△DHF ∽△BMF ∴BM ：DA=BE ：DE,DH ：BM=DF ：BF 又∵BE=EF=FD,所以BE ：DE=DF ：BF=1：2 ∴AD=2BM,BM=2DH,所以AD=4DH,∴AH=43AD ∴S △AMH:S 平行四边形ABCD=83。

变式：如图，在平行四边形ABCD 中，AE:EB=2:3.则△AEF 和△CDF 的周长比______.解答：∵四边形ABCD 是平行四边形，∴AB=CD,AB//CD ， ∴∠EAF=∠DCF ，∠AEF=∠CDF ，∴△AEF ∽△CDF ，S ΔABD S ΔACD =a bh b a H D CBAh a S=12ah E S ΔADE S ΔABC =a 2b 2b a DCBA P ED CBAM 1F 1E 1M EFA BC∴△AEF 的周长：△CDF 的周长=AE ：CD=2：5.变式：如图,E 为平行四边形ABCD 的边AB 延长线上的一点,且BE:AB=2:3，△BEF 的面积为4,则平行四边形ABCD 的面积为_________.答案∵四边形ABCD 是平行四边形，∴AD=CB,CB//AD,BC//AB ∴△DEF ∽△AEB ， ∵DE:AB=2:3，∴DE:AE=2:5，∴S △DEF:S △AEB=4:25， ∵△BEF 的面积为4，∴S △AEB=25， ∴S 四边形ABFD=S △AEB−S △DEF=21， ∵AD=CB ，DE:AD=2:3，∴DEBC=23，∵AB//CD ，∴△BEF ∽△CDF ，∴S △DEF:S △CBF=4:9，∴S △CBF=9， ∴S 平行四边形ABCD=S 四边形ABFD+S △CBF=21+9=30【例题】如图,EE 1//FF 1//MM 1//BC,若AE=EF=FM=MB,则S △AEE 1:S 四边形EE 1F 1F:S 四边形FF 1M 1M:S 四边形MM 1CB 为_____.答案:设S △AEE 1=x∵ EE 1//FF 1∴ △AEE 1∽△AFF 1 (平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的 三角形与原三角形相似)∴ 2211AF AE AFF S AEE S =∆∆ (相似三角形面积比等于对应边的平方比) ∵ AE=EF ∴ 21=AF AE ∴ 4111=∆∆AFF S AEE S ∴ S △AFF1=x 4 ∴ S 四边形EE 1F 1F=x 3同理可得 S 四边形FF 1M 1M=x 5 S 四边形MM1CB=x 7∴ S △AED:S 四边形EE1F1F:S 四边形FF 1M 1M:S 四边形MM 1CB=1:3:5:7变式：如图，在△ABC 中，FG//DE//AB ，且AF=FG=CG 。

相似比与面积比的关系
面积比=（相似比）的平方，相似三角形的面积比等于相似比的平方。

设小三角形的面积为s，底长为a高为h，则小三角形的面积为s=1/2*a*b。

设大三角形的面积为S，底长为ka高为kh，则大三角形的面积为
S=1/2*ka*kb=1/2*k^2ab。

S/s=(k^2ab)/(a*b)=k^2。

扩展资料：
相似三角形的性质：
1. 相似三角形对应角相等，对应边成比例。

2. 相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比。

3. 相似三角形周长的比等于相似比。

4. 相似三角形面积的比等于相似比的平方。

5. 相似三角形内切圆、外接圆直径比和周长比都和相似比相同，内切圆、外接圆面积比是相似比的平方。

6. 若a/b =b/c，即b²=ac，b叫做a,c的比例中项。

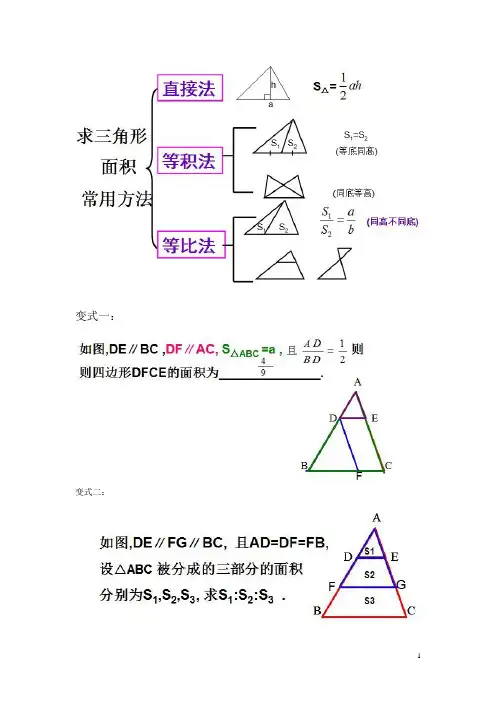
变式一：变式二：变式三：变式四：变式五：变式六：变式七：中考习题：作业题：在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ； （2）当x 为何值时，⊙O 与直线BC 相切？（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠ANM ＝∠C ．∴ △AMN ∽ △ABC ．∴ AM AN AB AC=，即43x AN=．A B C M N P图 1O A B C M N D图 2 OAB M N 图 3O A MNPOBD 图 2∴ AN ＝43x ． ……………2分 ∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x ＜4） ………………3分 （2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ． 在Rt △ABC 中，BC ． 由（1）知 △AMN ∽ △ABC ．∴ AM MN AB BC=，即45x MN=．∴ 54MN x =，∴ 58OD x =． …………………5分 过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==．在Rt △BMQ 与Rt △BCA 中，∠B 是公共角， ∴ △BMQ ∽△BCA ． ∴ BM QM BC AC=．∴ 55258324xBM x ⨯==，25424AB BM MA x x =+=+=． ∴ x ＝4996． ∴ 当x ＝4996时，⊙O 与直线BC 相切．…………………………………………7分 （3）随点M 的运动，当P 点落在直线BC 上时，连结AP ，则O 点为AP 的中点．∵ MN ∥BC ，∴ ∠AMN =∠B ，∠AOM ＝∠APC∴ △AMO ∽ △ABP ． ∴ 12AM AO AB AP ==． AM ＝MB ＝2．故以下分两种情况讨论：① 当0＜x ≤2时，2Δ83x S y PMN ==．∴ 当x ＝2时，2332.82y =⨯=最大 …………………………………………8分 ② 当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ．∵ 四边形AMPN 是矩形， ∴ PN ∥AM ，PN ＝AM ＝x ． 又∵ MN ∥BC ， ∴ 四边形MBFN 是平行四边形． ∴ FN ＝BM ＝4－x ．∴ ()424PF x x x =--=-． 又△PEF ∽ △ACB ．图 4P 图 3∴ 2PEF ABCS PF AB S ∆∆⎛⎫= ⎪⎝⎭． ∴ ()2322PEF S x ∆=-． ……………………………………………………… 9分 MNP PEF y S S ∆∆=-＝()222339266828x x x x --=-+-．……………………10分当2＜x ＜4时，29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭．∴ 当83x =时，满足2＜x ＜4，2y =最大． ……………………………11分 综上所述，当83x =时，y 值最大，最大值是2． ……………………………12分总结：1.直接法:根据三角形的面积公式解题2.等积法:等底等高的两三角形面积相等.3.等比法:将面积比转化为线段比.①等底(或同底)的三角形面积之比等于高之比. ②等高(或同高)的三角形面积之比等于对应底之比. ③相似三角形的面积比等于相似比的平方.。

相似三角形的中线和面积比较相似三角形是指具有相同形状但不一定相等的三角形。

在相似三角形中，中线和面积是两个重要的性质，它们之间存在一定的关系。

本文将探讨相似三角形的中线和面积的比较。

一、相似三角形的定义和性质相似三角形是指两个三角形的对应角相等，并且对应边成比例。

具体而言，若三角形ABC与三角形DEF相似，则有以下关系成立：1. 角的对应关系：∠A = ∠D，∠B = ∠E，∠C = ∠F。

2. 边的成比例关系：AB/DE = BC/EF = AC/DF。

相似三角形具有许多重要的性质，其中包括中线和面积的特点。

二、相似三角形中线的比较在相似三角形中，中线与对边之间也存在一定的比例关系。

设三角形ABC与三角形DEF相似，比例系数为k（即AB/DE = BC/EF = AC/DF = k）。

1. 中线比较：若AD和DF分别为三角形ABC和三角形DEF的中线，则它们的长度比为k/2。

即AD/DF = k/2。

证明：根据相似三角形的性质，有AB/DE = BC/EF = AC/DF = k。

由于AD是三角形ABC的中线，因此AD = (1/2)AC。

同理，DF = (1/2)EF。

代入比例关系式中，得到AD/DF = (1/2)AC/(1/2)EF = AC/EF = k。

由此可知，在相似三角形中，中线的长度比是对应边长度比的一半。

2. 比较示例：举例说明中线比较的关系。

设有相似三角形ABC和三角形DEF，比例系数为k = 2。

则根据中线比较的结论，三角形ABC 的中线AD和三角形DEF的中线DF的长度比为2/2=1。

即AD/DF = 1。

三、相似三角形面积的比较在相似三角形中，面积与边长的关系是二次的比例关系。

设三角形ABC与三角形DEF相似，比例系数为k（即AB/DE = BC/EF = AC/DF = k）。

1. 面积比较：若S1和S2分别为三角形ABC和三角形DEF的面积，则它们的面积比为k^2。

相似三角形之面积问题知识点：若两三角形相似，则两三角形的面积比等于相似比的平方。

模型一：A 形相似下的面积问题：已知DE ∥BC若：21=AB AD 则 41=ABC ADE S S △△, 31=BCDE ADE S S 梯形△图1例1.如图1，在△ABC 中，DE ∥BC,1).______:2:1:21==S S DB AD ，则._______:94)221==BC DE S S ，则：：若练习1：如图1,在△ABC 中，DE ∥BC,1).______:3:1:21==S S DB AD ，则._______:______,:54)221===BC DE AB AD S S ，则：：若._______:74)221==BC DE S S ，则：：若练习2.如图1,在△ABC 中，DE ∥BC,DB AD S S BCED AD E :41:，求：梯形△=例2.若DE ∥FG ∥BC ，且DE ，FG △ABC 的面积三等分，若BC=9，则FG 的长为_____.练习3若DE ∥FG ∥BC ，且DE ，FG △ABC 的面积三等分，若BC=15，则FG 的长为_____，DE+FG=_______.模型二：以平行四边形一边为相似三角形的一条边。

例3.平行四边形ABCD 中，点F 在DC 边上，且FC:FD=1：3，则。

△△__________:=EAB EFC S S A DFBC E练习4.如图，F 在平行四边形ABCD 的边DC 的延长线上，连接AF 交BC 于E ，且CE ：BE=1：3，若△EFC 的面积等于a ，求平行四边形的面积．练习 5.在平行四边形ABCD 中，E 为DC 边上的中点，AE 交BD 于点O,._______,cm 92==AO B D O E S S △△则模型三：三角形中等高模型：若两个三角形等高，则面积比就等于底边之比。

AE 若31=EC AE 则._____=BCEABE S S △△ B CA 若._______31==ADCABD S S CD BD △△，则B D C例4.在正方形ABCD中，若AB=4，AE：EC=1：3，求△BCE的面积。

相似三角形面积和边之比的关系相似三角形是初等几何学中的一个重要概念。

它描述了两个或更多个三角形具有相同形状但可能不同尺寸的特性。

在相似三角形中，我们可以观察到面积和边之间存在着一种重要的关系。

在本文中，我们将深入探讨这个关系，以及它对几何学的应用。

让我们回顾一下相似三角形的定义。

相似三角形是指具有相同形状但不一定相同尺寸的三角形。

两个三角形相似的条件是它们的对应角度相等，并且对应边的比例相等。

根据这个定义，我们可以得出结论：相似三角形的对应边之比等于它们的面积之比。

设有两个相似三角形ABC和DEF，它们之间的对应边之比为AB/DE。

现在，让我们考虑这两个三角形的面积。

根据几何学的面积公式，三角形的面积等于底边乘以高并除以2。

三角形ABC的面积可以表示为：Area_ABC = (1/2) * AB * h_ABC，其中h_ABC是三角形ABC的高。

同样地，三角形DEF的面积可以表示为：Area_DEF = (1/2) * DE *h_DEF，其中h_DEF是三角形DEF的高。

由于三角形ABC和DEF是相似的，它们的对应边之比等于AB/DE。

假设相似比例为k，即AB/DE = k。

我们可以将这个比例代入到上述的面积公式中，得到：Area_ABC = (1/2) * (k * DE) * h_ABC = (1/2)* k * DE * h_ABC，以及Area_DEF = (1/2) * DE * h_DEF。

通过比较这两个表达式，我们可以得出结论：相似三角形的对应边之比等于它们的面积之比。

这个结论对于几何学的应用非常重要。

通过相似三角形的面积和边的关系，我们可以解决各种有关比例和比率的问题。

在房地产领域，我们可以利用相似三角形的面积和边之比来估算房屋的价格。

通过测量房屋的长度和宽度，并找到一个相似三角形来比较，我们可以根据它们的边之比来计算房屋的面积，从而估算出房屋的价值。

相似三角形的面积和边之比还可以应用于地理学和天文学中。

初中数学相似直角三角形的面积比例是否相等相似直角三角形的面积比例是相等的。

设两个相似的直角三角形为△ABC和△DEF，其中△A和△D是直角。

根据三角形相似的性质，我们知道对应角度相等，并且对应边长之比相等。

因此，我们可以得出以下结论：1. 面积比例关系：相似的直角三角形的面积之比等于对应边长之比的平方。

设直角边分别为AB和DE，对应边长分别为BC和EF，根据相似三角形的性质，有以下比例关系成立：面积(△ABC)/面积(△DEF) = (BC/EF)^2证明：根据三角形的面积公式，△ABC的面积为(1/2)*AB*BC，△DEF的面积为(1/2)*DE*EF。

因此，我们需要证明(1/2)*AB*BC / (1/2)*DE*EF = (BC/EF)^2。

首先，我们知道AB/DE = BC/EF，根据这个比例关系，我们可以将DE表示为AB的一个倍数：DE = k*AB，其中k为一个常数。

将DE代入△DEF的面积公式，我们得到面积(△DEF) = (1/2)*k*AB*EF。

将AB和EF代入△ABC的面积公式，我们得到面积(△ABC) = (1/2)*AB*BC。

将面积(△ABC)和面积(△DEF)代入面积比例关系中，我们得到：面积(△ABC)/面积(△DEF) = (1/2)*AB*BC / ((1/2)*k*AB*EF) = BC/EF * (1/k)由于AB/DE = BC/EF，所以1/k = DE/AB = (k*AB)/AB = k。

因此，面积(△ABC)/面积(△DEF) = BC/EF * (1/k) = BC/EF * k = (BC/EF)^2。

这个证明表明，如果两个直角三角形是相似的，它们的面积之比等于对应边长之比的平方。

这个性质在解决与相似直角三角形相关的问题时非常有用，可以帮助我们确定未知的面积比例关系。

相似三角形边长与面积比的关系
相似三角形的边长比与面积比是有一定关系的。

设有两个相似三角形ABC和DEF，它们的边长比为k（k>0），则它们的面积比为k。

也就是说，如果相似三角形ABC和DEF的边长比为2∶3，则它们的面积比为4∶9。

证明如下：设∠A=α，∠B=β，∠C=γ，∠D=δ，∠E=ε，∠F=ζ，AB=c，BC=a，AC=b，DE=fc，EF=fa，DF=fb，S(ABC)为三角形ABC 的面积，S(DEF)为三角形DEF的面积。

根据三角形面积公式有：
S(ABC)=0.5×b×c×sinα
S(DEF)=0.5×fb×fa×sinζ
因为三角形ABC和DEF相似，所以有：
∠A=∠D=α
∠B=∠E=β
∠C=∠F=γ
根据正弦定理和相似三角形的定义有：
a/b=f×fa/c
c/b=f×fb/a
将上述式子代入S(ABC)和S(DEF)的公式中，可得：
S(ABC)/S(DEF)=(b×c×sinα)/(fb×fa×sinζ)
=(b×c×sinα)/(b×a×sinβ)×(a×f×fa)/(fb×c×sinγ) =a/(fb)×f
=(a/f)
因为a/f=k（边长比），所以有：
S(ABC)/S(DEF)=k
所以，相似三角形的边长比为k（k>0）时，它们的面积比为k。

初中数学如何使用相似三角形的性质计算三角形的面积
要使用相似三角形的性质计算三角形的面积，可以利用相似三角形的面积比来求解。

当两个三角形相似时，它们的对应边的长度比相等，而对应角的度数也相等。

假设有两个相似的三角形ABC和DEF，它们的对应边长比为a:b，面积比为S₁:S₂。

如果已知三角形DEF的面积S₂和对应边长比a:b，那么可以使用以下公式计算三角形ABC的面积S₁：
S₁ = (a²/b²) * S₂
具体计算步骤如下：
1. 已知三角形DEF的面积S₂和对应边长比a:b。

2. 计算面积比的平方。

根据相似三角形的性质，面积比的平方等于对应边长比的平方：
(S₁/S₂)² = (a/b)²
3. 求解S₁。

将已知的面积比带入公式，可以得到三角形ABC的面积S₁：
S₁ = (a²/b²) * S₂
通过以上公式，可以利用已知相似三角形的面积比和对应边长比来计算另一个三角形的面积。

需要注意的是，在使用相似三角形的性质计算面积时，要确保两个三角形确实是相似的，并且对应边长比已知准确。

总结起来，可以利用相似三角形的面积比来计算三角形的面积。

根据已知的面积比和对应边长比，使用相似三角形的面积比公式计算另一个三角形的面积。

相似三角形的面积比例与边长比例的关系相似三角形是指具有相同形状但大小不同的两个三角形。

在几何学中，相似三角形的面积比例与边长比例之间存在着一定的关系。

本文将探讨相似三角形的面积比例与边长比例之间的关系，并解释其原理。

一、相似三角形的定义和性质相似三角形是指具有相同形状但大小不同的两个三角形。

当两个三角形的对应角度相等时，它们为相似三角形。

相似三角形的性质如下：1. 对应角相等性质：如果两个三角形的对应角相等，则它们为相似三角形。

2. 边长比例性质：相似三角形的对应边长之比相等。

二、相似三角形的面积比例相似三角形的面积比例与边长比例之间存在着一定的关系。

假设有两个相似三角形，其边长比例为k，则面积比例为k^2。

证明：设两个相似三角形的面积分别为S1和S2，边长比例为k。

则可以得到以下等式：S1 = (1/2) * a1 * b1 * sin(A1)S2 = (1/2) * a2 * b2 * sin(A2)其中，a1和a2分别为三角形的底边，b1和b2分别为对应的高，A1和A2为对应的顶角。

根据相似三角形的性质，可以得到以下等式：a2 = k * a1b2 = k * b1A2 = A1将以上等式代入面积公式中，得到：S2 = (1/2) * (k * a1) * (k * b1) * sin(A1)= k^2 * (1/2) * a1 * b1 * sin(A1)= k^2 * S1因此，面积比例S2/S1 = k^2。

由此可见，相似三角形的面积比例与边长比例的平方成正比。

三、应用举例下面通过一个实际问题来应用相似三角形的面积比例与边长比例的关系。

问题：已知一个三角形ABC，其边长分别为a、b、c，三角形的高为h。

设另一个三角形DEF为相似三角形，且其边长比例为k（即DE=k*AB，DF=k*AC，EF=k*BC）。

求证：三角形DEF的面积为三角形ABC面积的k^2倍。

解答：首先根据相似三角形的性质，可以得到三角形DEF的边长为DE=k*AB，DF=k*AC，EF=k*BC。

相似三角形中的面积问题教案
一、教学目标
1．理解并初步掌握相似三角形周长的比等于相似比，面积的比等于相似比的平方．2．能用三角形的性质解决简单的问题．
二、重点、难点
1．重点：相似三角形的性质与运用．
2．难点：相似三角形性质的灵活运用，及对“相似三角形面积的比等于相似比的平方”性质的理解，特别是对它的反向应用的理解，即对“由面积比求相似比”的理解．3．难点的突破方法
（1）相似三角形的性质：①对应角相等，对应边成比例；②相似三角形周长的比等于相似比；③面积的比等于相似比的平方．（还可以补充④相似三角形对应高的比等于相似比）
（2）应用相似三角形的性质，其前提条件是两个三角形相似，不满足前提条件，不能应用相应的性质．如：两个三角形周长比是，它们的面积之比不一定是，因为没有明确指出这两个三角形是否相似，以此教育学生要认真审题．
（3）在应用性质2“相似三角形面积的比等于相似比的平方”时，要注意有相似比求面积必要平方，这一点学生容易掌握，但反过来，由面积比求相似必要开方，学生往往掌握不好，教学时可增加一些这方面的练习．如：如果两个相似三角形面积的比为3∶5 ，那么它们的相似比为________，周长的比为________．。

初中数学如何计算相似三角形的面积比例在初中数学中，计算相似三角形的面积比例是一个重要的概念。

相似三角形具有相似的形状，即它们的对应角度相等，并且对应边长成比例。

本文将详细介绍如何计算相似三角形的面积比例。

相似三角形的面积比例计算方法：计算相似三角形的面积比例，我们可以使用以下方法：1. 边长比例法：如果两个三角形相似，它们的面积比例等于对应边长的平方比例。

具体步骤如下：（1）比较两个相似三角形的对应边长，将它们按照相同的顺序进行比较。

（2）计算对应边长的比值的平方，即两个边长之间的比例关系的平方。

例如，已知三角形ABC和DEF相似，边长比例为AB/DE = AC/DF = BC/EF = 2/3，已知三角形ABC的面积为S1，我们可以通过边长比例计算出对应三角形DEF的面积S2。

解：根据边长比例法，我们有：S1/S2 = (AB/DE)^2 = (AC/DF)^2 = (BC/EF)^2 = (2/3)^2S1/S2 = 4/9因此，面积比例S1/S2的值为4/9。

2. 高度比例法：如果两个三角形相似，它们的面积比例等于对应高度的平方比例。

具体步骤如下：（1）比较两个相似三角形的对应高度，将它们按照相同的顺序进行比较。

（2）计算对应高度的比值的平方，即两个高度之间的比例关系的平方。

例如，已知三角形ABC和DEF相似，高度比例为hA/hD = hB/hE = hC/hF = 3/4，已知三角形ABC的面积为S1，我们可以通过高度比例计算出对应三角形DEF的面积S2。

解：根据高度比例法，我们有：S1/S2 = (hA/hD)^2 = (hB/hE)^2 = (hC/hF)^2 = (3/4)^2S1/S2 = 9/16因此，面积比例S1/S2的值为9/16。

总结：计算相似三角形的面积比例是初中数学中的一个重要概念。

我们可以使用边长比例法和高度比例法来计算相似三角形的面积比例。

通过比较对应的边长或高度之间的比值的平方，我们可以确定两个三角形的面积比例关系。

三角形面积比问题专题训练一、相似三角形面积比定理：相似三角形的面积比等于相似比的平方、练习1、△ABC 中，D 、E 分别是AB 、AC 的中点，则△ADE 与四边形DBCE 的面积比为 。

2、△ABC 中，D 是AB 上一点，∠B =∠ACD ，AB=7，AC=4，则S △ABC :S △ACD = 。

3、△ABC ∽△ABC=二、等高或等底的三角形面积比定理：等高（或同高）的三角形面积比=底之比，等底（或同底）的三角形面积比=高之比。

练习2、（1）如左图，D 在BC 上，BD:CD=3：2,则=∆∆ABC ABD S S =∆∆ADC ABD S S（2）如右图，AD 是△ABC 的高，点G 在AD 上 ，若AG:DG=4：3，则=∆∆G B CABC S S , 三、综合以上方法解决面积问题1、如图，在梯形ABCD 中，AB ∥CD ，AC 和BD 相交于点O 。

如果41:：=∆∆AOB O DC S S ，则ODC S ∆:AOD S ∆= 。

2、如图，在△ABC 中，D ，E 分别在AB ，BC 上，且DE ∥AC ，若4:1:=∆∆CD E BD E S S ,则=∆∆ACDE BD E S S :( )A ．1：16 B.1：18 C.1：20 D.1：243、如图在△ABC 中，过AB 上一点M 作MN ∥BC 交AC 于点N ，使得△AMN 的面积与梯形MNCB 的面积之比为4：5,连接BN ，MC 交于点G ，若△BGC 的面积为1，则△ABC 的面积等于（ ）A.3B.4C.5D.211 A B C D E E AC BD D A B C G D A B C O DA B C E D B C A GM N A B C。

相似三角形的有关面积问题复习引入：求三角形而积常用方法1、面积公式:2、等髙法：3、相似三角形:【精选例题】【例题】如图，平行四边形ABCD中，AE:EB=2:3,则SΔAPE≡SΔCPD=解答:4:25。

【例题】如图，AC是平行四边形ABCD的对角线, 且BE=EF=FD Z求SΔ AMH: S忖训边形ABCD的值。

解答：Y平行四边形ABCD…∙∙AB∕∕CD, AD//BC・•・△ BME〜A DAE, △ DHF〜心BMF・•・ BM： DA=BE: DE z DH: BM=DF: BF・・• BE=EF=FD z所以BE： DE=DF: BF=I: 23・•・ AD=2BM z BM=2DH^WAD=4DH z∕. AH=-AD43・・AMHZS ∙f⅛PK⅛J∣;ABCD=—G8变式：如图，在平行四边形ABCD中∙AE:EB=2:3.则厶AEF和厶CDF的周长比_____ 解答：∙.∙四边形ABCD是平行四边形,.∙. AB=CD,AB//CD, SAADE_a 2 SΔABC"b22SAABD aSΔACD'b又・•・ Z EAF=Z DCF, Z AEF=Z CDF, /. A AEF〜△ CDF,•••△AEF 的周长：Δ CDF 的周长=AE： CD=2: 5・变式：如图,E为平行四边形ABCD的边AB延长线上的一点,且BE:AB=2:3, Δ BEF的面积为4,则平行四边形ABCD的而积为_________ ・答案T四边形ABCD是平行四边形，・•・AD=CB Z CB∕∕AD z BC∕∕AB.∙. △ DEF- △AEB, •・• DE:AB=2:3,・•・DE:AE=2:5> .Β.SΔ DEF:SAAEB=4:25,T ∆ BEF的面积为4,・•・SAAEB二25,・•・ S HI边形ABFD=SAAEB-SA DEF=21,TAD=CB, DE:AD二2:3, /. DEBC=23∙∙.∙AB∕∕CD, /. ∆ BEF^ Δ CDF,二S A DEF:SACBF=49 A SΔ CBF=9,.,.S 平行Pa边影ABCD=S 円边形ABFD+S° CBF=21+9=30【例题】如图,EE√∕FF√∕MM√∕BC,若AE=EF=FIVI=MB,则SA AEExSNgEEIHF:S啊边形FFiWM:SN奶MMlCB 为_____ 答案:设SA AEEI=X∙.∙ EE√∕FF1.∙. Δ AEE I- ∆ AFF1（平行于三角形一边的宜线和其它两边（或两边的延长线）相交,所构成的三角形与原三角形相似）•・・WAEE = 竺（相似三角形而积比等于对应边的平方比）S S AF F； AF2•・• AE=EF/. ∆∆ = l ・•・S^AEE∖=I .・・SΔ AFFl= 4x .∙. Sl f Q边形 EE l F I F=3x AF 2 S s AFF y 4同理可得S w⅛mFFιMιM= 5x S UQ边形MMICB二IX/. SA AED:S JM边形EEIFIF:S Wi4® FFIMIM:S 曲边形MMiCB==1:3:5:7变式：如图，在Δ ABC中，FG//DE//AB,且AF=FG=CGo设Δ ABC被分成的三部分的面积分别为S“ S?和求Si: S2： S3C解答：∙∙∙F∖ G为AC边上的三等分点,D、E为AB边上的三等分点・•・ AF： AG： AC=I: 2： 3T FD//EG//BC 八SΔCFG:SΔ CDE： SΔ CAB=I: 4： 9, .β. SI： S2： S3=l: 3： 5变式：如图，DE//FG//BC,设ZkABC 被分成的三部分的而积分别为S1,S2,S3,且SI 二S2=S3,则AD:DF:FB 二 答案：∖∙ S1=S2,・・ S A ADE:SAAFG=4:2,.β. DE 2:FG 2=1:2, .β. DE:FG=l:%/2 :同理，DE:BC=1：A /3, Λ DE ： FG ： BC=I: √2 : √3 o【例题】如图：在梯形ABCD 中,AD∕/BCBC=2AD,对角线AC 与BD 相交于点0,把4 ABO z Δ BCO,Δ COD z Δ DOA 的面积分别记作S1,S2,SXS4,则下列结论中,正确的是（）a・•・ ON:MN=2:3,・•・ 2S Δ AOB=S Δ OBC Z S2=2S1.同理 S2=2S3./. S2=2S1=2S3=4S4变式:如图表示一个梯形两条对角线相交于一点，则图中面枳相等的三角形共有（）o【例题】如图，点D 、E 、F 分别是△ ABC 三边上的中点•若△ ABC 的而积为12cm ∖则厶DEF 的而积为 cm 2.答：•••点D. E 、F 分别是AABC 三边上的中点， ••・DF 、DE 、EF 为Δ ABC 的中位线， ∙∙∙ Δ ABCS Δ DEF,相似比为1:2,所以而积比为1:2, S ΔABC: S Δ DEF=4:1=12:S A DEF> S Δ DEF=3cm 2・变式：如图，分别取等边三角形ABC 各边的中点D, E, F,得ADEE 若△ ABC 的边长为a.C. S1=S3・•・ ONzOM=AD:BC=I:2,D. S1÷S3=S2+S4ABOC, 答案：D即（1）∆ DEF与厶ABC相似吗?如果相似，相似比是多少?⑵分别求出这两个三角形的面积。

中考数学复习之相似三角形有关的面积问题（学案）知识与方法梳理 处理面积问题的三种方法 1. 公式法2. 割补法（分割求和，补形作差）3. 转化法（相似类、同底类、共高或等高类）利用常见结构进行转化是在复杂背景下处理面积问题的通常思路，在转化过程中需要结合背景的特点．动态背景：要抓住变化过程中所求面积不变的特征；函数背景：优先考虑公式法，或者割补之后采用公式法，也可结合几何特征进行转化； 探索规律背景：根据结构特征确定第一项的处理办法，后续进行类比． 面积问题中的常见结构举例例1：如图，在Rt ABC △中，1D 是斜边AB 的中点.过1D 作11D E AC ⊥于E 1，连接1BE 交1CD 于2D ，过2D 作22D E AC ⊥于2E ，连接2BE 交1CD 于3D ，过3D 作33D E AC ⊥于3E ，连接3BE 交1CD 于4D …如此继续.11E BD 1S S ∆=22E BD 2S S ∆=33E BD 3S S ∆=nn E BD n S S ∆=则n S =____________ABC S △（用含n 的代数式表示）．32E 1D 4D 3D 2D 1CBA分析：题目中的相似三角形非常之多，三角形的面积关系也非常之多，这是面积问题同学们需要面对的第一大难题，处理好这些关系，才能最终解决问题； 解：1.易知E 1为AC 的中点，S ∆ABE1=12S ∆ABC ，D1为AB 的中点，S ∆BD1E1=12S ∆ABE1，故S ∆BDE =14S ∆ABC ；2. D 1E 1||BC ，1112D E AC =，故E 2为E 1C 的三等分点，12113BE E BCE S S ∆∆=，D 2为BE 1的三等分点，故222123BD E BE E S S ∆∆=，112BE C ABC S S ∆∆=，故2219BD E ABC S S ∆∆=3. 易知221123D E D E =,111AC 2D E =，故221AC 3D E =，D 3为BE 2的四等分点，231211212BE E BE E ABC S S S ∆∆∆==，，而33116BD E ABC S S ∆∆=；综合上述，猜想S n =21(1)ABCS n ∆+练习题1. 如图，△ABC 的面积为63cm 2，D 是BC 上的一点，且BD :CD =2:1，DE △AC 交AB 于点E ，延长DE 到F ，使FE :ED =2:1，连接CF ，则△CDF 的面积为 ．FED CBA2. 如图，在△ABC 中，D ，E 分别是边AB ，AC 的中点，G 为EC 的中点，连接DG 并延长交BC 的延长线于点F ，BE 与DF 交于点O ．若△ADE 的面积为S ，则四边形BOGC 的面积为_______．G ODCAE BF3. 如图，在梯形ABCD 中，AB △CD ，AB =3CD ，对角线AC ，BD 交于点O ，中位线EF 与AC ，BD 分别交于点M ，N ，则图中阴影部分的面积是梯形ABCD 面积的（ ） A ．12 B ．13 C ．14 D ．474. 如图，点A 1，A 2，A 3，A 4在射线OA 上，点B 1，B 2，B 3在射线OB 上，且A 1B 1△A 2B 2△A 3B 3，A 2B 1△A 3B 2△A 4B 3．若△A 2B 1B 2，△A 3B 2B 3的面积分别为1，4，则图中阴影部分的面积为_______．12345.如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合）．以BD，BF为邻边作平行四边形BDEF，又AP△BE，且AP=BE（点P，E在直线AB的同侧），若14BD AB，则△PBC的面积与△ABC的面积的比值是___________．ABCD EFPG6.如图，已知直线l1：y=23x+83与直线l2：y=-2x+16相交于点C，直线l1，l2分别交x轴于A，B两点，矩形DEFG的顶点D，E分别在l1，l2上，顶点F，G都在x轴上，且点G与点B重合，那么S矩形DEFG:S△ABC=____________．7.已知：如图，DE是△ABC的中位线．点P是DE的中点，连接CP并延长交AB于点Q，那么S△DPQ:S△ABC=_________．QP EDC BA8.如图，在△ABC中，CE:EB=1:2，DE△AC．若△ABC的面积为S，则△ADE的面积为____________．9.如图，已知△ABC△△DCE△△HEF，三条对应边BC，CE，EF在同一条直线上，连接BH，分别交AC，DC，DE于点P，Q，K．若△DQK的面积为2，则图中阴影部分的面积为__________．10.如图，在△ABC中，AB=AC，M，N分别是AB，AC的中点，D，E为BC上的点，连接DN，EM交于点F．若AB=13cm，BC=10cm，DE=5cm，则图中阴影部分的面积为___________．参考答案1．422．7 4 S3．C4．21 25．3 46．8:9 7．1:248．2 9 S9．26 10．30cm2。

相似三角形与圆的面积比例相似三角形是指具有相同形状但大小不同的两个三角形。

在数学中，我们常常会遇到需要计算相似三角形的面积比例的问题。

而在这些问题中，如果结合了圆形，便会产生一些有趣的性质和定理。

一、相似三角形的面积比例给定两个相似三角形，假设它们的边长比例为a:b，那么它们的面积比例为(a^2):(b^2)。

这个结论可以通过几何推导或者利用面积的性质来证明。

我们先来看一个简单的例子。

假设有两个相似三角形，它们的两条边的长度比例为2:3，求它们的面积比例。

设相似三角形的面积分别为S1和S2，根据面积的性质，我们有S1/S2=(边长比例)^2=(2/3)^2=4/9。

所以，这两个相似三角形的面积比例为4:9。

二、现在，我们来探讨一下相似三角形和圆的面积比例。

假设有一个固定大小的圆和一个相似于它的三角形，我们想要知道它们的面积比例。

首先，我们需要知道相似三角形的面积比例可以表示为边长比例的平方。

因此，如果可以将这个相似三角形转化为一个带有圆形的问题，我们就可以得到相似三角形与圆的面积比例。

考虑一个等腰直角三角形，它的两条直角边长度为a。

我们可以将这个等腰直角三角形每个直角顶点到斜边的距离定义为圆的半径。

那么，这个等腰直角三角形将与半径为a的圆相似。

根据相似三角形的面积比例定理，这个等腰直角三角形的面积与半径为a的圆的面积的比例为(斜边长度/半径)^2=(a/a)^2=1:1。

这意味着，无论这个等腰直角三角形的大小如何变化，它的面积与半径为a的圆的面积始终保持相等。

三、应用举例在实际问题中，我们可以利用相似三角形与圆的面积比例来解决一些有关面积或者比例的题目。

例1：已知一个半径为4的圆与一个相似三角形的面积比例为1:4，求该相似三角形的面积。

解：根据相似三角形与圆的面积比例，我们可以得到(圆的面积/相似三角形的面积)=1/4。

而已知圆的半径为4，代入圆的面积公式S=πr^2，我们可以得到(π*4^2)/(相似三角形的面积)=1/4。

相似三角形面积
相似三角形的面积比等于相似比的平方。

三角分别相等，三边成比例的两个三角形叫做相似三角形。

相似三角形是几何中重要的证明模型之一，是全等三角形的推广。

全等三角形可以被理解为相似比为1的相似三角形。

相似三角形的面积比等于相似比的平方可通过三角形面积公式进行解释：
1、三角形的面积等同于底除以低除以二。

2、两个三角形的面积比即为：两个三角形“底乘以高除以二”的比值。

3、这里的底边和低的比值分别就是对应边的比，所以面积即为为对应边比的平方。

相似三角形的性质：
定义：相近三角形的对应角成正比，对应边变成比例。

定理：相似三角形任意对应线段的比等于相似比。

定理：相近三角形的面积比等同于相近比的平方。

相似三角形的特殊情况：
1.凡是全等的三角形都相近。

全等三角形是特殊的相似三角形，相似比为1。

反之，当相似比为1时，相似三角形为全等三角形。

2. 存有一个顶角或底角成正比的两个等腰三角形都相近。

由此，所有的等边三角形都相似。

两个相似三角形的面积之差
摘要：
1.相似三角形的定义和性质
2.相似三角形面积的计算方法
3.两个相似三角形面积之差的求解
4.实际应用和举例
正文：
1.相似三角形的定义和性质
相似三角形是指两个三角形的对应角度相等，对应边长成比例的图形。

相似三角形有一个重要的性质，就是它们的面积之比等于它们任意一条对应边的长度的平方之比。

2.相似三角形面积的计算方法
相似三角形的面积计算方法是：如果两个相似三角形的对应边长之比为a:b，那么它们的面积之比就是a:b。

3.两个相似三角形面积之差的求解
假设有两个相似三角形ABC 和DEF，它们的对应边长之比为a:b，那么它们的面积之比就是a:b。

如果ABC 的面积是S1，DEF 的面积是S2，那么S1-S2=S1(1-b/a)。

4.实际应用和举例
这个公式在实际生活中有很多应用，比如在建筑设计中，如果我们知道一个建筑的模型，想要求出另一个相似建筑的面积，就可以使用这个公式。