附录3简单荷载作用下梁的挠度和转角
- 格式:pdf
- 大小:301.67 KB
- 文档页数:3
从图在该段中的变线段(T即为非粮馆举性段, 压液线可看出即整个拉伸过程可分为以下四个阶段。
* /)称线弹性段,其斜率即为弹性模量E,对应的最高应力值 虎克定律(r=Ec 成立。
而ab 段, 在该段内所产生的应变仍是弹性的, 但它与应力已不成正比。
b点相对立白 勺应力第五早材料力学 主讲:钱民刚 第一节 概论材料力学是研究各种类型构件(主要是杆)的强度、刚度和稳定性的学科,它提供 了有关的基本理论、计算方法和试验技术,使我们能合理地确定构件的材料、尺寸 和形状,以达到安全与经济的设计要求。
♦一、材料力学的基本思路 (一)理论公式的建立 理论公式的建立思路如下:(一)低碳钢材料拉伸和压缩时的力学性质低碳钢(通常将含碳量在0.3%以下 的钢称为低碳钢,也叫软钢)材料拉伸和压缩时的 (7- e 曲线如图5-1所示。
陶度箓n------- 搬面设计为确保构件不致因强度/、丸而破坏, 应使其最——该啊瓯丽于材料的极限应力0- u,物出射和 (力与姻(美系)* 变形外力 T ]表小,即临界前载应力力布1£配IX没有屈服阶段,也酸 _ 曲线的一条割线的斜率,作为其弹性模量。
它 1故衡量铸铁拉伸强度的唯一指标就是它被拉断时/,在较小的拉应力作用下即被拉断,且其延伸率很小,故铸铁TE与拉伸相比,可看出这类材料的抗压能力要比抗拉 事蝌性变形也较为蛾显。
破坏断口为斜断面,这表明试件是因m max对于塑性材料制成的杆,通常取屈服极限①良或名义屈服极限(T该段内应力基本上不变,但应变却在迅速增长,而且在该段内所产生的应变 成分,除弹性应变外,还包含了明显的塑性变形,该段的应力最低点 (7S 称为屈服 极限。
这时,试件上原光滑表面将会出现与轴线大致成 45。
的滑移线,这是由于试 件材料在45。
的斜截面上存在着最大剪应力而引起的。
对于塑性材料来说,由于屈 服时所产生的显著的塑性变形将会严重地影响其正常工作,故(7S 是衡量塑性材料强度的一个重要指标。



梁的挠曲线、挠度和转角的概念
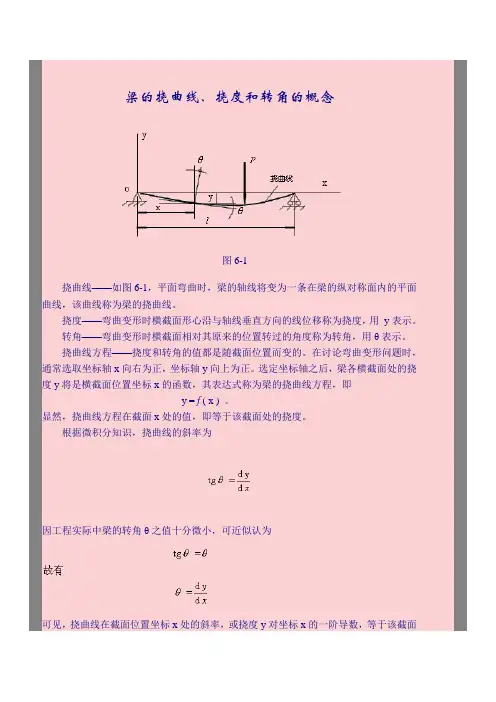
图6-1
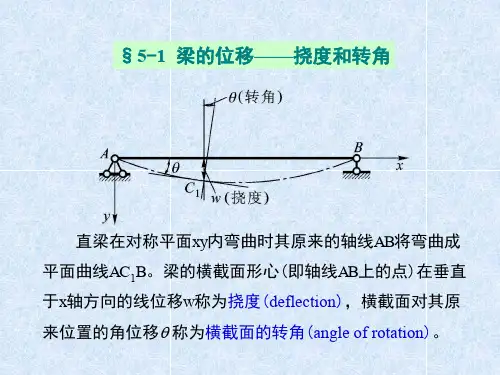
挠曲线——如图6-1,平面弯曲时,梁的轴线将变为一条在梁的纵对称面内的平面曲线,该曲线称为梁的挠曲线。
挠度——弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度,用y表示。
转角——弯曲变形时横截面相对其原来的位置转过的角度称为转角,用θ表示。
挠曲线方程——挠度和转角的值都是随截面位置而变的。
在讨论弯曲变形问题时,通常选取坐标轴x向右为正,坐标轴y向上为正。
选定坐标轴之后,梁各横截面处的挠度y将是横截面位置坐标x的函数,其表达式称为梁的挠曲线方程,即
y = f ( x ) 。
显然,挠曲线方程在截面x处的值,即等于该截面处的挠度。
根据微积分知识,挠曲线的斜率为
因工程实际中梁的转角θ之值十分微小,可近似认为
可见,挠曲线在截面位置坐标x处的斜率,或挠度y对坐标x的一阶导数,等于该截面
的转角。
关于挠度和转角正负符号的规定:在如图6-1选定的坐标系中,向上的挠度为正,逆时针转向的转角为正。





惯性矩、截面系数、弯矩图计算公式汇总附录1 截面图形的几何性质提要:不同受力形式下杆件的应力和变形,不仅取决于外力的大小以及杆件的尺寸,而且与杆件截面的几何性质有关。
当研究杆件的应力、变形,以及研究失效问题时,都要涉及到与截面形状和尺寸有关的几何量。
这些几何量包括:形心、静矩、惯性矩、惯性半径、极惯性矩、惯性积、主轴等,统称为“平面图形的几何性质”。
研究上述这些几何性质时,完全不考虑研究对象的物理和力学因素,作为纯几何问题加以处理。
平面图形的几何性质一般与杆件横截面的几何形状和尺寸有关,下面介绍的几何性质表征量在杆件应力与变形的分析与计算中占有举足轻重的作用。
附1.1 截面的静矩与形心任意平面几何图形如图1.1所示。
在其上取面积微元dA,该微元在yOz坐标系中的SSy=?zdA,Sz=?ydA坐标为z、y。
设静矩为,则有:AA图1.1 静矩的概念 (附1.1)静矩的量纲为长度的3次方。
由于均质薄板的重心与平面图形的形心有相同的坐标zC和yC。
则A?zC=?z?dA=Sy A———————————————————————————————————————————————由此可得薄板重心的坐标zC为zC=?AzdAA=SyA 同理有yC=Sz A?260? 材料力学所以形心坐标或zC=SyA,yC=SzA(附1.2)Sy=AzC,Sz=AyC由式(附1-2)得知,若某坐标轴通过形心轴,则图形对该轴的静矩等于零,即yC=0,Sz=0;zC=0,则Sy=0;反之,若图形对某一轴的静矩等于零,则该轴必然通过图形的形心。
静矩与所选坐标轴有关,其值可能为正,负或零。
如一个平面图形是由几个简单平面图形组成,称为组合平面图形。
设第i块分图形的面积为Ai,形心坐标为 yCi,zCi ,则其静矩和形心坐标分别为———————————————————————————————————————————————Sz=?AiyCi,Sy=?AizCii=1i=1nniCi(附1.3)SyC=z=A?Ayii=1nCi?Ai=1n,zC=SyA=?Azi=1nn(附1.4) ———————————————————————————————————————————————i?Ai=1i【例附1.1】求图1.2所示半圆形的Sy,Sz及形心位置。
简支梁挠度计算公式均布荷载作用下工字梁的最大挠度在梁跨中间,其计算公式如下: Ymax = 5 ql ^ 4 / (384 ej)。
地点:ymax是中间的最大挠度梁的跨度(CM)Q为均匀线荷载(kg / cm)E为工字梁弹性模量,对于工程结构钢,E = 2100000 kg / cm ^ 2 J为工字梁截面惯性矩,可在型钢表(cm ^ 4)中求得也可转换为kn;以m为单位ra=rb=p/2mc=mmax=pl/4fc=fmax=pl^3/48eiθa=θb=pl^2/16ei符号意义及单位p——集中载荷,n;q——均布载荷,n;r——支座反力,作用方向向上者为正,n;m——弯矩,使截面上部受压,下部受拉者为正,nm;q——剪力,对邻近截面所产生的力矩沿顺时针方向者为正,n;f——挠度,向下变位者为正,mm;θ——转角,顺时针方向旋转者为正,°;e——弹性模量,gpa;i——截面的轴惯性矩,m^4;ξ=x/l,ζ=x'/l,α=a/l,β=b/l,γ=c/l简支梁就是承载两端竖向荷载,而不提供扭矩的支撑结构。
体系温变、混凝土收缩徐变、张拉预应力、支座移动等都不会在梁中产生附加内力。
简支梁受力简单,为力学简化模型。
将简支梁体加长并越过支点就成为外伸梁,简支梁支座的铰接是固定铰支座、滑动铰支座的基数级跨中弯距Mka:Mka= (Md+Mf) ×VZ/VJ+ΔMs/VJ -MsMka= (Md+Mf)×1.017/1.0319+△Ms/1.0319-Ms=(17364.38+0)×1.017/1.0319+4468.475/1.0319-164.25 = 21279.736(kN·m)计算各加载级下跨中弯距:Mk= (k(Mz+Md+Mh+Mf) -Mz) ×VZ/VJ+ΔMs/VJ -MsMk=(k(Mz+Md+Mh+Mf) -Mz)×1.017/1.0319 +△Ms/1.0319―Ms=(k (31459.38+17364.38+24164.75+0)-31459.38)×1.017/1.0319+4468.475/1.0319-164.25=71934.601×k-26839.0389(kN·m)计算静活载级系数:Kb = [Mh/(1+μ) +Mz+Md+Mf]/(Mh+Mz+Md+Mf)Kb= [24164.75/1.127+31459.38+17364.38+0]/ (24164.75+31459.38+17364.38+0)=0.963计算基数级荷载值:Pka=Mka/α=21279.736/54.75=388.671(kN)计算各荷载下理论挠度值:f = 2 P [ L+2 (L/2-Χ1)(3L-4(L/2-Χ1)) +2 (L/2-Χ2)(3L-4(L/2-Χ2)) ] / 48EI/1000=0.01156P。