几种常用梁在简单载荷作用下的变形转角和挠度

3. 应用叠加原理的若干情况 1 ) 荷载的分解或重组
q m
q
L/2 L/2
L
F
q
q
m L/2 L/2
F
例
q0
EI
A 求图示自由端的挠度。
L2
L2
q0
L
w1
q0
w3
B
w2
L2
L2
w1
q0 L4 8EI
w2
q0 L 24
8EI
q0 L4 128EI
w3
B
L 2
q0 L 23
6EI
L 2
q0 L4 96EI
wA
w1
w2
w3
41q0 L4 384EI
2) 逐段刚化法
依据： 若结构可分为若干部分，且各部分在荷载作用下的 变形不是相互独立的，那么，结构中 A 点的位移是各个部 分在这一荷载作用下的变形在 A 点所引起的位移的叠加。
A EI a
变形刚体
F
F
Fa 2
B
C
a/2
wwww1122
B (F1, F2,, Fn ) B1(F1) B2 (F2 ) Bn(Fn )
yB (F1, F2,, Fn ) yB1(F1) yB2 (F2 ) yBn(Fn )
叠加法的特征： 1、梁在简单载荷作用下挠度、转角应为已知或有变形表可查； 2、叠加法适用于求梁个别截面的挠度或转角值。
分析和讨论
q
在下列不同的支承方 式中，哪一种刚度最高？
q
q
分析和讨论
q
梁由混凝土材料制成，如果横截面从左图改为右图，能 够改善强度吗？能够改善刚度吗？
梁的材料由普通钢改为优质钢，能够改善强度吗？ 梁的材料由普通钢改为优质钢，能够改善刚度吗？

工程中虽然经常是限制弯曲变形，但在另 一些情况下，常常又利用弯曲变形达到某 种要求。例如，叠板弹簧应有较大的变形， 才可以更好地起缓冲减振作用。弹簧扳手 要有明显的弯曲变形，才可以使测得的力 矩更为准确。 弯曲变形计算除用于解决弯曲刚度问题外， 还用于求解静不定系统和振动计算。所以 弯曲变形的研究是非常的重要的。
悬臂梁受集中力的情况
悬臂梁受集中力偶的情况
悬臂梁受分布力的情况
绞支梁受集中力的情况
绞支梁受集中力偶的情况
绞支梁受分布力的情况
四、用叠加法求弯曲变形：

1. 叠加法原理（力的独立性原理）： 在小变形前提下，当构件或结构同时作用几 个载荷时，如果各载荷与其产生的效果(支 反力，内力，应力和位移、变形等)成线性 关系(互不影响，各自独立)，则它们同时作 用所产生的总效果等于各载荷单独作用时 所产生的效果之和(代数和、矢量和)：
2. 求梁的弯曲变形的叠加法是：
分别求出各载荷单独作用时的变形(位移)，然 后把各载荷在同一处引起的位移进行叠加 (代数叠加)。

谢谢观赏！
梁在简单载荷作用下变形学在学习工程中的查询。

工程中对某些受弯杆件除强度要求外，往往还有 刚度要求，即要求它变形不能过大。以机床主轴 为例，若其变形过大，将影响齿轮的啮合和轴承 的配合，造成磨损不匀，产生噪音，降低寿命， 还会影响加工精度；以吊车梁为例，当变形过大 时，将使梁上小车行走困难，出现爬坡现象，还 会引起较严重的振动；再以化工厂的管道为例， 弯曲变形如果超过容许数值，就会造成物料的淤 积，影响输送；较长的回转滚筒，弯曲变形过大， 就会引起脆性材料的开裂；电机转子的轴变形过 大，可能导致与定子相碰。所以，若变形超过允 许数值，即使仍然是弹性的，也被以为是一种失 效。

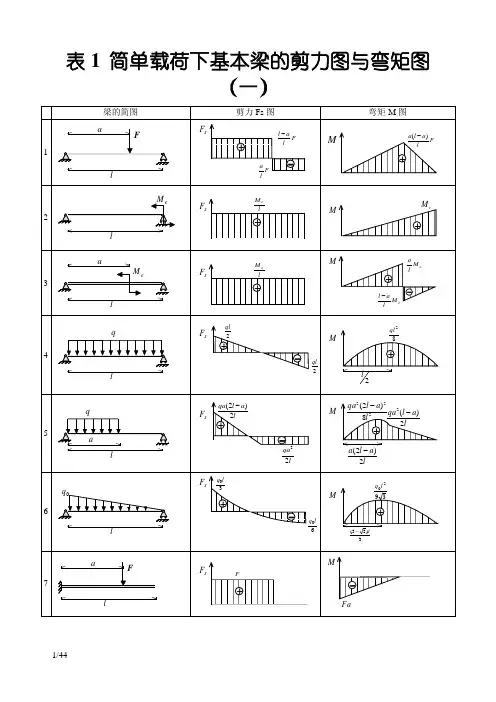
表1 简单载荷下基本梁的剪力图与弯矩图（一）注：外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5 3/444/445/446/447/448/449/44注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：m axy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

2）三跨等跨梁的内力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

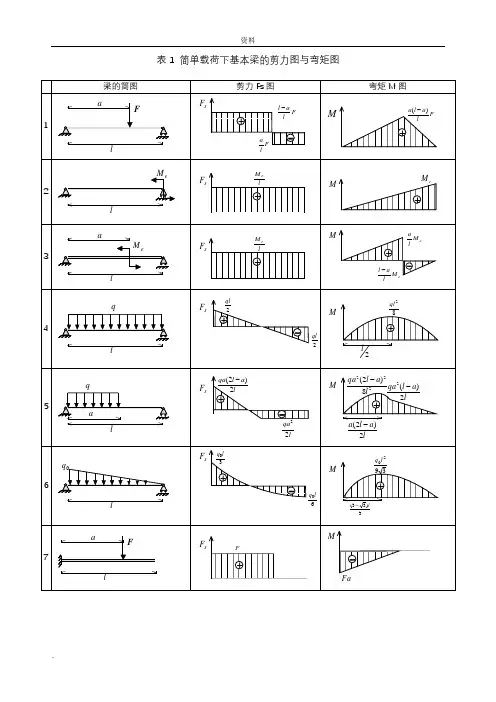
表1 简单载荷下基本梁的剪力图与弯矩图注：外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5 .......资料.注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EI w 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

2）三跨等跨梁的内力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

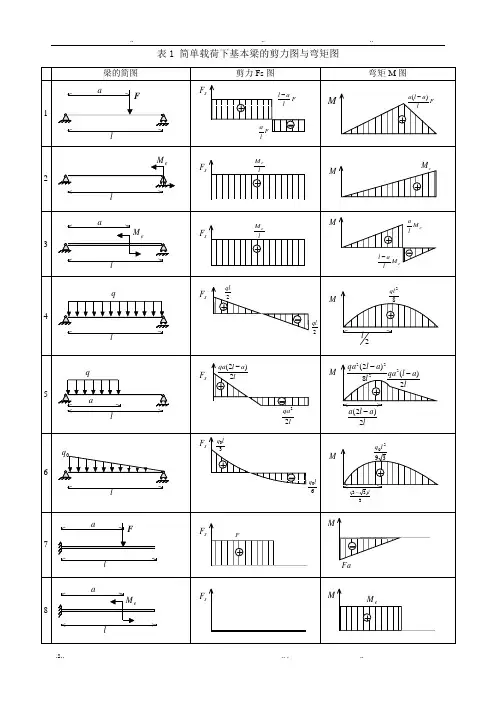
表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5.s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ..注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

.. .. .. 2．单跨梁的力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

2）三跨等跨梁的力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

a xl
在 x l / 2处
y 0.5l


Fb
(3l 2 4b 2 ) 48 EI
yqx(l32lx2x3) 2E 4 I
A

B


ql3 24EI
x

l 2
ymax


5ql4 384EI
梁的简图
第九章 梁的弯曲变形
挠曲线方程
y6M EI(xllx)2(lx)
yC1
aB
qa4 2EI
yC2


qa4 8EI
3）叠加 y C y C 1 y C 2 2 q E 4a 8 I q E 4a I 5 8 q E 4( a I)
第九章 梁的弯曲变形
例9-5 悬臂梁跨度为 l =2m，截面为矩形，宽b = 100mm，高h =120mm，材料的弹性模量E=210GPa， 梁上载荷如图所示，求自由端A的挠度。
挠曲线方程 y f (x)
第九章 梁的弯曲变形
二、挠度和转角
挠度：截面形心线位 移的垂直分量称为该 截面的挠度，用 y 表 示，一般用 ymax 表示 全梁的最大挠度。
转角：横截面绕中性轴转动产生了角位移，此角
位移称转角，用 表示。小变形时，转角 很小，
则有以下关系：
tanydy
1
(x)

M(x) EI
曲线 y f(x)的曲率
1
(x)
(1yy2)3/2
二阶小量
y (1y2)3/2
M(x) EI
挠曲轴线 近似微分方程
y M(x) EI
第九章 梁的弯曲变形
挠曲轴线 近似微分方程
y

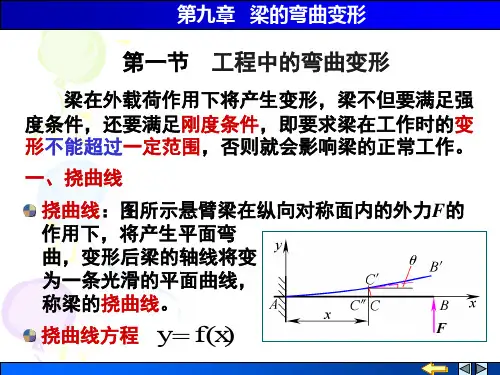
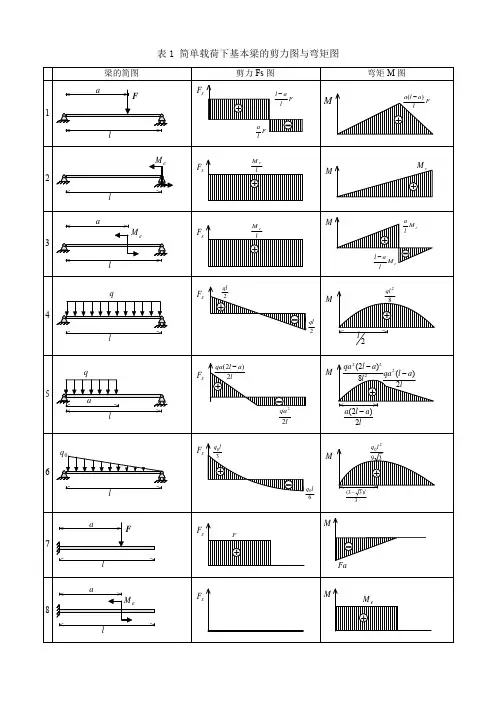
表1 简单载荷下基本梁的剪力图与弯矩图注：外伸梁 =悬臂梁 + 端部作用集中力偶的简支梁2 各种载荷下剪力图与弯矩图的特征表表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰∙=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN ·m V B 左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝11.76kN/m ，求边跨最大跨中弯矩。

表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F la F l al -+-F la l a )(-+M2leMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lq asF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注：外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线 或零点极值表3 各种约束类型对应的边界条件约束类型 位移边界条件力边界条件（约束端无集中载荷）固定端0=w ,0=θ —简支端0=w0=M 自由端—0=M ,0=S F注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰∙=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

表1 简单载荷下基本梁的剪力图与弯矩图之邯郸勺丸创作注：外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的鸿沟条件注：力鸿沟条件即剪力图、弯矩图在该约束处的特征.经常使用截面几何与力学特征表表2-5 创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）.基本计算公式如下：⎰•=AdAy I 22．W 称为截面抵当矩（mm 3）, 它暗示截面抵当弯曲变形能力的年夜小, 基本计算公式如下：max y I W =3．i 称截面回转半径（mm ）, 其基本计算公式如下：A I i =4．上列各式中, A为截面面积（mm2）, y为截面边缘到主轴（形心轴）的距离（mm）, I为对主轴（形心轴）的惯性矩.5．上列各项几何及力学特征, 主要用于验算构件截面的承载力和刚度.创作时间：二零二一年六月三十日2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EI w 100ql 表中系数4⨯=. 2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EI w 100Fl 表中系数3⨯=. 2）三跨等跨梁的内力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EI w 100ql 表中系数4⨯=.2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EI w 100Fl 表中系数3⨯=. 3）四跨等跨连续梁内力和挠度系数 表2-13注：同三跨等跨连续梁.4）五跨等跨连续梁内力和挠度系数 表2-14注：同三跨等跨连续梁.创作时间：二零二一年六月三十日（2）不等跨连续梁的内力系数（表2-15、表2-16）1）二不等跨梁的内力系数表2-15创作时间：二零二一年六月三十日注：1．M＝表中系数×ql21；V＝表中系数×ql1；2．（M max）、（V max）暗示它为相应跨内的最年夜内力.2）三不等跨梁内力系数表2-16创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日注：1．M＝表中系数×ql21；V＝表中系数×ql1；2．（M max）、（V max）为荷载在最晦气安插时的最年夜内力.创作时间：二零二一年六月三十日4．双向板在均布荷载作用下的内力及变形系数表（表2-17~表2-22） 符号说明如下：刚度 )1(1223υ-=Eh K 式中 E ——弹性模量；h ——板厚； ν——泊松比；ω、ωmax ——分别为板中心点的挠度和最年夜挠度；M x ——为平行于l x 方向板中心点的弯矩； M y ——为平行于l y 方向板中心点的弯矩； M x 0——固定边中点沿l x 方向的弯矩； M y 0——固定边中点沿l y 方向的弯矩. 正负号的规定：弯矩——使板的受荷面受压者为正； 挠度——变位方向与荷载方向相同者为正.四边简支 表2-17三边简支, 一边固定 表2-18两边简支, 两边固定表2-19 一边简支, 三边固定表2-20四边固定表2-21两边简支, 两边固定表2-225．拱的内力计算表（表2-23）各种荷载作用下双铰抛物线拱计算公式表2-23注：表中的K为轴向力变形影响的修正系数.（1）无拉杆双铰拱1）在竖向荷载作用下的轴向力变形修正系数式中 I c——拱顶截面惯性矩；A c——拱顶截面面积；A——拱上任意点截面面积.当为矩形等宽度实腹式变截面拱时, 公式I＝I c/cosθ所代表的截面惯性矩变动规律相当于下列的截面面积变动公式：此时, 上式中的n可表告竣如下形式：下表中列出了矩形等宽度实腹式变截面拱的n值.f/ln2）在水平荷载作用下的轴向力变形修正系数, 近似取K＝1（2）带拉杆双铰拱1）在竖向荷载作用下的轴向力变形修正系数式中 E——拱圈资料的弹性模量；E1——拉杆资料的弹性模量；A1——拉杆的截面积.2）在水平荷载作用下的轴向力变形修正系数（略去拱圈轴向力变形影响）式中 f——为矢高；l——为拱的跨度.6．刚架内力计算表内力的正负号规定如下：V——向上者为正；H——向内者为正；M——刚架中虚线的一面受拉为正.（1）“┌┐”形刚架内力计算（表2-24、表2-25）“┌┐”形刚架内力计算表（一）表2-34“┌┐”形刚架内力计算表（二）表2-35（2）“”形刚架的内力计算（表2-26）”形刚架的内力计算表表2-26。

常用挠度公式常用的挠度公式指的是用于计算结构物挠度的公式，挠度是指结构物在受力作用下发生的形变。

挠度公式的应用十分广泛，涉及到工程、建筑、力学等领域。

在工程中，我们经常需要计算结构物的挠度，以评估其受力性能和安全性。

挠度公式是用来描述结构物在受力作用下发生的弯曲变形的数学公式。

常用的挠度公式有梁的挠度公式和杆的挠度公式。

我们来看梁的挠度公式。

梁是一种常见的结构物，在很多工程中起着承载和支撑作用。

梁的挠度是指梁在受力作用下发生的弯曲形变程度。

梁的挠度公式可以根据梁的几何形状、材料性质和受力情况进行推导。

常用的梁的挠度公式有三种，分别是简支梁的挠度公式、悬臂梁的挠度公式和悬臂梁的挠度公式。

简支梁的挠度公式是根据梁的几何形状和受力情况推导出来的。

简支梁的挠度公式可以用来计算在梁两端施加集中力或均布力时梁的挠度。

简支梁的挠度公式是根据梁的受力平衡方程和弯矩-挠度关系推导出来的。

简支梁的挠度公式可以表述为：挠度=（集中力或均布力乘以梁的长度的平方）/（48倍的弹性模量和惯性矩的乘积）。

悬臂梁的挠度公式是用来计算在梁一端施加集中力或均布力时梁的挠度的公式。

悬臂梁的挠度公式可以根据悬臂梁的受力平衡方程和弯矩-挠度关系推导出来。

悬臂梁的挠度公式可以表述为：挠度=（集中力或均布力乘以梁的长度的平方）/（3倍的弹性模量和惯性矩的乘积）。

杆的挠度公式是用来计算杆在受力作用下发生的挠度的公式。

杆的挠度公式可以根据杆的几何形状、材料性质和受力情况进行推导。

常用的杆的挠度公式有两种，分别是短杆的挠度公式和长杆的挠度公式。

短杆的挠度公式是用来计算短杆在受力作用下发生的挠度的公式。

短杆的挠度公式可以根据短杆的受力平衡方程和弯矩-挠度关系推导出来。

短杆的挠度公式可以表述为：挠度=（集中力或均布力乘以杆的长度的平方）/（2倍的弹性模量和截面面积的乘积）。

长杆的挠度公式是用来计算长杆在受力作用下发生的挠度的公式。

长杆的挠度公式可以根据长杆的受力平衡方程和弯矩-挠度关系推导出来。

弯曲变形粱的挠度与转角（一）挠曲线在外力作用下，梁的轴线由直线变为光洁的弹性曲线，梁弯曲后的轴线称为挠曲线。

在平面弯曲下，挠曲线为梁形心主惯性平面内的一条平面曲线v=f(x)(见图5-8-1)。

（二）挠度与转角梁弯曲变形后，梁的每一个横截面都要产生位移，它包括三部分：1. 挠度梁横截面形心在垂直于轴线方向的线位移，称为挠度，记作v。

沿梁轴各横截面挠度的变化规律，即为梁的挠曲线方程。

v=f(x)2．转角横截面相对本来位置绕中性轴所转过的角度，称为转角，记作θ。

小变形情况下，3．此外，横截面形心沿梁轴线方向的位移，小变形条件下可忽略不计。

(三)挠曲线近似微分方程在线弹性范围、小变形条件下，挠曲线近似微分方程为上式是在图5—8—l所示坐标系下建立的。

挠度w向下为正，转角θ顺时针转为正。

积分法计算梁的位移按照挠曲线近似微分方程(5—8—1)，积分两次，即得梁的转角方程和挠度方程，即由第1 页/共6 页式中积分常数C、D，可由梁的边界条件来决定。

当梁的弯矩方程需分段列出时，挠曲线微分方程也需分段建立，分段积分。

于是全梁的积分常数数目将为分段数目的两倍。

为了决定所有积分常数，除利用边界条件外，还需利用分段处挠曲线的延续条件(在分界点处左、右两段梁的转角和挠度均应相等)。

用叠加法求梁的位移（一）叠加原理几个荷载同时作用下梁的任一截面的挠度或转角等于各个荷载单独作用下同一截面挠度或转角的总和。

（二）叠加原理的适用条件叠加原理仅适用于线性函数。

要求挠度、转角为梁上荷载的线性函数，必须满意： 1．材料为线弹性材料；2．梁的变形为小变形；3．结构几何线性。

（三）叠加法的特征1．各荷载同时作用下挠度、转角等于单独作用下挠度、转角的总和，应该是几何和，同一方向的几何和即为代数和。

2．梁在容易荷载作用下的挠度、转角应为已知或可查手册。

3．叠加法相宜于求梁某一指定截面的挠度和转角。

[例 5—8—1] 用积分法求图5—8—3所示各梁的挠曲线方程时，试问应分为几段?将浮上几个积分常数? 并写出各梁的边界条件和延续条件。

表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝m ，每跨各有一集中荷载F ＝，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－××52）＋（－××5）＝（－）＋（）＝－·m V B 左＝（－××5）＋（－×）＝（－）＋（－）＝－[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝m ，求边跨最大跨中弯矩。

作品编号：DG13485201600078972981创作者：玫霸*表1 简单载荷下基本梁的剪力图与弯矩图注：外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA y I 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：max y IW =3．i 称截面回转半径（mm ），其基本计算公式如下：AI i = 4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EI w 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

2）三跨等跨梁的内力和挠度系数 表2-12注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

跳板，木板横截面尺寸b=500 mm，h=50 mm，木板材料的许 用应力［σ］=6 MPa 。 试求：
(1) 一体重为700 N (2) 要求两名体重均为700 N的工人抬着1500 N的货物安全 走过，木板的宽度不变，重新设计木板厚度h。
第6章 弯 曲
解 (1) 计算弯矩的最大值Ｍmax。当工人行走到跳板中央
(2) 横截面上的弯矩在数值上等于该截面左侧(或右侧）所 有外力对该截面形心的力矩的代数和。
第6章 弯 曲
为了使所求得的剪力与弯矩符合前面的符号规定，按此 规律计算剪力时，截面左侧梁上外力向上取正值，向下取负 值，截面右侧梁上外力向下取正值，向上取负值；计算弯矩 时，截面左侧梁上外力对该截面形心的力矩顺时针转向取正 值，逆时针转向取负值，截面右侧外力对该截面形心的力矩 逆时针转向取正值，顺时针转向取负值。可以将这个规则归 纳为一个简单的口诀：左上右下，剪力为正；左顺右逆，弯 矩为正。
第6章 弯 曲 图 6.10
第6章 弯 曲 解 设截面m-m与B端之间的距离为x，取m-m截面的右段
为研究对象，画出受力图，如图6.10(b)所示。 根据平衡条件：
由Fs=qx可绘出剪力图，如图6.10(c)所示；由 描点可绘出弯矩图，如图6.10(d)
第6章 弯 曲
6.3 弯曲时的正应力与强度计算
m，材料的许用应力[σ]=150 MPa， 求此悬臂梁的许可载荷。
图 6.15
第6章 弯 曲 解 绘出悬臂梁的弯矩图，如图6.15(b)所示。 图中，Mmax=Fl=4000F 梁的横截面抗弯截面系数为
由梁的弯曲正应力强度条件得
因此, 悬臂梁的许可载荷为F=25 000 N。
第6章 弯 曲 【例6.5】 某建筑工地上, 用长l=3 m的矩形截面木板做

2EI 16EI


2EI B
l/2
B
p
EI C
l/2
p
c
c
P MB=Pl/2
B
C
B B
wc2
C

w2B

qa4 8EI z

qa3 6EI z
(l
a)
2C
qa3 6EI z

wB
w1B
w2B
qL4 8EI z
qa4 8EI z
qa3 6EI z
(l a)

q
3l 4 [
la3

a4
]
6EIz 4
4
x
qdx
q
解法2 A
a C dx
B
x
ql
w
距离A端为x的dx梁段上的荷载可视为集中力P=qdx
q x
B
6EI
以x=l 代入以上方程可得自由端的挠度和转角：
wB
wx xl
ql 2 24EI
l 2 4l 2 6l 2
ql 4 8EI

B (x) xl ql (l 2 3l 2 3l 2 ) ql3
6EI
c1 a
wB
;
wx
x0
ql 4
利用两个边界条件: w xl xl 0
由此：
c1

ql 3 6
,
c2

ql 4 24

ql 3 6
l


ql 4 8
8EI B (x) x0
ql 3

横截面的转角q 也就是挠曲线在该相应点的切线与x轴之
间的夹角，从而有转角方程：
q tanq w f x
(a)
(b)
直梁弯曲时的挠度和转角这两个位移不但与梁的弯曲
变形程度(挠曲线曲率的大小)有关，也与支座约束的条件
有关。图a和图b所示两根梁，如果它们的材料和尺寸相同， 所受的外力偶之矩Me也相等，显然它们的变形程度(也就 是挠曲线的曲率大小)相同，但两根梁相应截面的挠度和
x

a
3
x3

l2
b2
x
左、右两支座处截面的转角分别为
qA
q1
|x0
Fb l 2 b2 6lEI
Fabl b
6lEI
qB
q2
|xl


Fabl
6lEI
a
当a>b时有
qmax qB

Fabl a
6lEI

根据图中所示挠曲线的大致形状可知，最大挠度wmax 所在w 0 处在现在的情况下应在左段梁内。令左段梁的
从几何方面来看，平面曲线的曲率可写作
1
w
x 1 w2 3/2
式中，等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量，而w"是q = w' 沿x方
向的变化率，是有正负的。
再注意到在图示坐标系中，负弯矩对应于正值w" ，正弯矩对
应于负值的w" ，故从上列两式应有
右段梁 (a x l)
q1 w1
Fb 2lEI
1 3
l2 b2

x
2

结构梁知识讲解范文结构梁是一种常见的结构元素，广泛应用于建筑工程和桥梁工程中。

它是由水平梁和竖向柱子组成的平面框架，主要用于承载和传递荷载。

下面将对结构梁的常见类型、设计原则和施工方法进行详细讲解。

一、结构梁的常见类型1.矩形梁：矩形梁是最常见的结构梁类型，其截面形状为矩形。

矩形梁适用于小跨度和荷载较小的情况下，承载能力较弱。

2.T型梁：T型梁的截面形状为T字形，其特点是上部翼缘较宽，适用于大跨度和荷载较大的情况，承载能力较强。

3.箱形梁：箱形梁可以看作是由两个矩形梁组成的结构，上下两个矩形梁通过垂直的薄壁连接起来，构成一个箱形的梁体。

箱形梁在承载能力和刚度上都具有较强的优势，适用于大跨度和大荷载的情况。

4.悬臂梁：悬臂梁是一种梁的延伸形式，梁的一端固定在墙上或支墩上，另一端悬挂在空中。

悬臂梁常用于桥梁工程中，承载能力强，但需要注意悬臂端的支撑和固定。

二、结构梁的设计原则1.强度原则：结构梁在设计时必须满足承受荷载的强度要求。

设计人员需要根据荷载的类型和大小，选择适当的梁的截面形状和尺寸，以确保梁具有足够的强度承受荷载。

2.刚度原则：结构梁在设计时还需要满足一定的刚度要求。

刚度是指梁在荷载作用下变形的能力。

设计人员需要根据结构的变形要求，选择适当的梁的截面形状和尺寸，以确保梁具有足够的刚度。

3.稳定性原则：结构梁的设计还需要考虑其稳定性。

结构梁在荷载作用下不能发生失稳现象，设计人员需要通过适当的支撑和固定措施，确保梁的稳定性。

三、结构梁的施工方法1.预制梁施工：预制梁是在工厂进行加工制作的梁体，施工时直接安装到现场。

预制梁可以通过钢模板或木模板进行制作，然后在工厂中进行混凝土浇筑，最后再进行养护。

预制梁施工可以提高工程的施工效率和质量。

2.现浇梁施工：现浇梁是指在现场进行混凝土浇筑的梁体，施工时需要搭设模板和支撑体系，并按照设计要求进行混凝土浇筑。

现浇梁施工需要注意混凝土的配合比例和浇筑工艺，以确保梁的质量和强度。