向量的内积与向量组的正交变换

向量的内积与施密特正交化过程向量的内积是线性代数中重要的概念，它不仅可以表述两个向量之间的夹角关系，还可以用于正交化过程中的计算。

施密特正交化是一种将一组线性无关的向量组转化为一组正交向量组的过程。

本文将分为以下几个部分介绍向量的内积和施密特正交化过程。

一、向量的内积A·B=a1b1+a2b2+...+anbn1.交换律：A·B=B·A2.分配律：(A+B)·C=A·C+B·C3.结合律：k(A·B)=(kA)·B=A·(kB)，其中k为实数4.内积为0的充要条件：当且仅当A、B正交（或垂直）时，A·B=0内积具有很多实际应用，比如：1.计算向量的模长：，A，=√(A·A)2. 计算向量之间的夹角：cosθ = (A·B)/(，A，B，)3.判断两个向量是否垂直：当且仅当A·B=0时，A与B垂直4.判断向量的正负性：当A·B>0时，夹角θ为锐角；当A·B<0时，夹角θ为钝角二、施密特正交化施密特正交化是一种将一组线性无关的向量组转化为一组正交向量组的过程。

假设有一组线性无关的向量A1,A2,...,An，施密特正交化的过程如下：1.选择一个向量a1作为正交向量组的第一个向量，令b1=a1/，a1，即单位化。

2.对于第k个向量向量Ak(k=2,3,...,n)，先将它与前k-1个向量的内积计算出来，然后减去它在前k-1个向量的投影：Ak' = Ak - (Ak·b1)b1 - (Ak·b2)b2 - ... - (Ak·bk-1)bk-1其中，bk = Ak'/，Ak'3. 重复步骤2，直到计算完所有向量。

经过施密特正交化，得到一组正交向量组b1,b2,...,bn。

施密特正交化的过程可以通过内积的运算来实现，将向量投影的概念用到了正交化过程中。

内积空间与正交变换的基本概念内积空间和正交变换是线性代数中重要的概念，它们在数学和物理等领域都有广泛的应用。

本文将介绍内积空间和正交变换的基本概念，以及它们在实际问题中的应用。

一、内积空间的定义和性质内积空间是指在定义了内积运算的向量空间。

内积运算是指将两个向量进行运算得到一个标量的运算，常用的内积运算有点乘和矩阵乘法等。

内积空间具有以下性质：1. 正定性：对于任意非零向量v，它的内积与自身的内积大于零，即(v, v) > 0。

当且仅当v等于零向量时，(v, v)等于零。

2. 线性性：对于任意向量u、v和w，以及任意标量a和b，有(u+v, w) = (u, w) + (v, w)和(au, v) = a(u, v)。

3. 对称性：对于任意向量u和v，有(u, v) = (v, u)。

内积空间可以是有限维的，也可以是无限维的。

常见的有限维内积空间是欧几里得空间，而无限维内积空间的例子有L2空间和Hilbert空间等。

二、正交变换的定义和性质正交变换是指保持向量间内积不变的线性变换。

设A是一个n阶实矩阵，若AA^T=I（其中I是单位矩阵），则称A是正交矩阵。

正交矩阵表示的线性变换称为正交变换。

正交变换具有以下性质：1. 保持内积：对于任意向量u和v，有(Au, Av) = (u, v)。

2. 保持长度：对于任意向量u，有||Au|| = ||u||，其中||u||表示向量u的长度。

3. 保持角度：对于任意两个非零向量u和v，它们的夹角与它们的像Au和Av的夹角相等。

正交变换常用于解决几何和物理问题，如旋转、平移和镜像等。

正交变换在图像处理和编码等领域也有广泛的应用。

三、内积空间与正交变换的关系内积空间和正交变换之间有着密切的联系。

给定一个内积空间V和一个正交变换矩阵A，可以构造一个新的内积空间W，其中向量的内积定义为(u, v) = (Au, Av)。

这个内积空间W称为V关于正交变换A的像空间。

正交变换的结论
正交变换是指将一个向量或者一个坐标系通过某种方法进行变换，使得变换前后的向量或坐标系之间保持角度不变，即原来是直角的地方变换后仍然是直角。

正交变换包括旋转、镜像和旋转加镜像等多种类型。

正交变换的结论有以下几点：
1. 正交变换保持向量长度不变：对于正交变换后的向量，它们的长度与变换前的向量长度相同。

这是因为正交变换不改变向量的大小，只改变了向量的方向。

2. 正交变换保持向量之间的夹角不变：对于任意两个向量，它们的夹角在经过正交变换后仍然保持不变。

这是因为正交变换不改变向量之间的夹角，只是改变了它们的方向。

3. 正交变换保持向量的内积不变：对于两个向量，它们的内积在经过正交变换后仍然保持不变。

这是因为向量的内积可以用向量的长度和夹角表示，而正交变换不改变向量的长度和夹角，因此内积也不会改变。

4. 正交变换可以用矩阵表示：对于一个n维向量的正交变换，可以用一个n*n 的正交矩阵来表示。

这个矩阵的每一列都是一个单位向量，且这些向量之间两两正交。

5. 正交变换的逆变换也是正交变换：对于一个正交变换，它的逆变换也是正交变换。

这是因为正交变换保持向量长度、夹角和内积不变，因此它的逆变换也会保持这些性质不变。

综上所述，正交变换是一种非常重要的数学工具，它在许多领域都有广泛的应用，如图像处理、信号处理、物理学等。

了解正交变换的性质和结论对于理解这些应用非常有帮助。

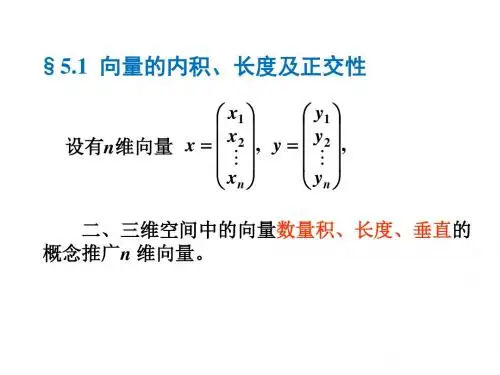
§2.4 向量的内积与正交向量组定义1 在中，设向量n R ,,2121⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n b b b a a a βα令,),(2211n n b a b a b a +++= βα称为向量与的内积.),(βααβ.),(βαβαT =例如，设则与的内积.)2,1,3,2(,)0,0,1,1(T T =−−=βααβ.12010312)1(),(=⨯+⨯+⨯+⨯−=βα内积是向量的一种运算，可用矩阵记号表示为根据定义1，不难验证内积具有下述性质：,0),)(4().,(),)(3().,(),)(2().,(),)(1(≥++=+==ααγβγαγβαβαβααββαk k 当且仅当时，有其中为中的向量，为常数.0=α.0),(=ααγβα,,n R k n R 定义2 对中的向量其长度向量长度也称为向量的范数.,),,,(21Tn a a a =α.),(22221n a a a +++== ααα例如，向量的长度T )2,1,1(=α.6211),(222=++==ααα向量长度具有下面的性质：当且仅当时，有.0α≥（1），0=α0=α.k k αα=•（2）(3)对任意向量，有βα,)1(.),(βαβα•≤如果上面不等式可写成这一等式称为柯西-施瓦次不等式.,),,,(,),,,(2121Tn T n b b b a a a ==βα.12121∑•∑≤∑===n i i n i i n i i i b a b a 证：当时，(1)式显然成立，以下. 令t 是一个实数，作向量. 由内积的性质(4)可知，不论t 取何值，一定有0=β0≠ββαγt +=,0),(),(≥++=βαβαγγt t对于不等式(1)当且仅当线性相关时，等号才成立.这由上述证明过程可以看出.用向量的长度去除向量，就得到一个单位向量，通常称为把向量单位化.即0),(),(2),(2≥++t t βββααα取代入上式，得),(),(βββα−=t ,0),(),(),(2≥−βββααα即),,)(,(),(2ββααβα≤两边开方得βαβα•≤),(βα,长度为1的向量称为单位向量，对于中的任一非零nR 向量，向量是一个单位向量.ααα1)0(≠ααα例1零向量与任意向量的内积为0，因此零向量与任意向量正交.定义3 如果两个向量与的内积等于0，即则称向量与互相正交. 记为.αβ,0),(=βααββα⊥例2 中的单位坐标向量组是两两正交的.n R n εεε,,,21 ⎩⎨⎧≠==)(0)(1),(j i j i j i εε定义4如果中的非零向量组两两正交，即则称该向量组为正交向量组.n R s ααα,,,21 ),,,2,1,;(0),(s j i j i j i =≠=αα定理4.1中的正交向量组线性无关.nR 证设为中的正交向量组，且有数，s ααα,,,21 n R s k k k ,,,21 .02211=+++s s k k k ααα 使得上式两边与向量组中的任意向量求内积，得i α,0)0,(),(2211==+++i s s i k k k ααααα 即,0),(),(),(2211=+++s i s i i k k k αααααα 由于，所以上式可化简为)(0),(j i j i ≠=αα,0),(1=i i k αα而为非零向量，于是得，从而线性无关.i α,0),(≠i i αα),,2,1(0s i k i ==s ααα,,,21.),(),(),(),(),(),(,),(),(),(),(,),(),(,111122221111222231111333111122211−−−−−−−−=−−=−==s s s ss s s s s ββββαββββαββββααβββββαββββααβββββααβαβ如果已知中的线性无关的向量组则可以生成正交向量组使这两个向量组等价.由一个线性无关向量组生成满足上述性质的正交向量组的过程，一般称为将该向量组正交化，将一个向量组正交化可以应用施密特正交化方法，其步骤如下：n R 12,,,,s ααα12,,,,s βββ对于中的线性无关向量组，令n R s ααα,,,21解.)21,21,1()1,1,0(21)1,1,1(30)0,1,1(),(),(),(),(,)1,1,0()1,1,1(33)2,0,1(),(),(,)1,1,1(222231111333111122211T T T T T T T T−=−−−−−=−−=−=−=−===ββββαββββααβββββααβαβ例3已知线性无关向量组将其化为正交向量组.,)0,1,1(,)2,0,1(,)1,1,1(321T T T −===ααα定义5设n 阶实矩阵Q ，满足则称Q 为正交矩阵.例如，单位矩阵E 为正交矩阵；在平面解析几何中，两直角坐标系间的坐标变换矩阵，是正交矩阵.正交矩阵具有下述性质：(1)若Q 为正交矩阵，则其行列式的值为1或-1.(2)若Q 为正交矩阵，则Q 可逆，且(3)若P , Q 都是正交矩阵，则它们的积PQ 也是正交矩阵.,E Q Q T =⎪⎭⎫⎝⎛−θθθθcos sin sin cos .1T Q Q =−定理4.2设Q 为n 阶实矩阵，则Q 为在正交矩阵的充分必要条件是其列(行)向量组是单位正交向量组.即Q 为正交矩阵的充分必要条件是其列向量组是单位正交向量组.类似可证，Q 的正交矩阵的充分必要条件是其行向量组是单位正证设，其中为Q 的列向量组.Q 是正交矩阵等价于而),,,(21n Q ααα =n ααα,,,21 ,E Q Q T =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n T n T n T n n T T T n T T T n T n T T T Q Q αααααααααααααααααααααααα 2122212121112121),,,(由此可知等价于E Q Q T =⎩⎨⎧=≠===),,2,1,;(0),,,2,1(1n j i j i n i j T i i T i αααα11例4正交阵的例子：定义6若Q 为正交矩阵，则线性变换y =Qx 为正交变换.由正交变换的定义可知这表明正交变换不改变向量的长度，这正是正交变换的优良特性..31313161616221210)2(;010100001)1(⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛−−⎪⎪⎪⎭⎫⎝⎛−−.x x x Qx Q x y y y T T T T ====。