高中数学必修一同步练习题库：对数函数(选择题：较难)

第1页共6页2023-2024学年高中数学必修一：对数函数一、选择题(每小题5分，共40分)1．已知a ＝log 213，b ＝5－3，c ＝212，则a ，b ，c 的大小关系为(A )A ．a <b <cB ．a <c <bC ．c <b <aD ．c <a <b解析：∵log 213<log 21＝0,0<5－3<50＝1,212＝2>1，∴a <b <c .故选A.2．若a >b ，则(C )A ．ln(a －b )>0B ．3a <3bC ．a 3－b 3>0D ．|a |>|b |解析：法一：不妨设a ＝－1，b ＝－2，则a >b ，可验证A ，B ，D 错误，只有C 正确．法二：由a >b ，得a －b >0.但a －b >1不一定成立，则ln(a －b )>0不一定成立，故A 不一定成立．因为y ＝3x 在R 上是增函数，当a >b 时，3a >3b ，故B 不成立．因为y ＝x 3在R 上是增函数，当a >b 时，a 3>b 3，即a 3－b 3>0，故C 成立．因为当a ＝3，b ＝－6时，a >b ，但|a |<|b |，所以D 不一定成立．故选C.3．若log 34·log 8m ＝log 416，则m 等于(D )A ．3B ．9C ．18D ．27解析：原式可化为log 8m ＝2log 34，∴13log 2m ＝2log 43，∴m 13＝3，m ＝27.4.下列函数中，随着x 的不断增大，增长速度最慢的是(B )A ．y ＝5x B ．y ＝log 5x C ．y ＝x 5D ．y ＝5x。

对数函数（简答题：较难）1、已知（1）求的值；（2）当（其中，且为常数）时，是否存在最小值，如果存在求出最小值；如果不存在，请说明理由；（3）当时，求满足不等式的的范围．2、已知函数是偶函数.（1）求的值；（2）若函数的图象与的图象有且只有一个公共点，求的取值范围.3、已知函数的图像恒过定点，且点又在函数的图像上.（1）求实数的值；（2）解不等式.4、已知向量，,且向量∥.（Ⅰ）求函数的解析式及函数的定义域；（Ⅱ）若函数,存在, 对任意,总存在唯一,使得成立, 求实数的取值范围.5、对于函数、、，如果存在实数使得，那么称为、的生成函数．(1) 下面给出两组函数，是否分别为、的生成函数？并说明理由；第一组：，，第二组：，，；(2) 设，，，生成函数．若不等式在上有解，求实数的取值范围；(3) 设，，取，生成函数图像的最低点坐标为．若对于任意正实数，且，试问是否存在最大的常数，使恒成立？如果存在，求出这个的值；如果不存在，请说明理由．6、已知函数为其定义域内的奇函数．（1）求实数的值；（2）求不等式的解集；（3）证明：为无理数．7、已知，且（1）当时，解不等式；（2）在恒成立，求实数的取值范围.8、已知函数，．（1）分别求函数与在区间上的极值；（2）求证：对任意，．9、已知函数，．（1）分别求函数与在区间上的极值；（2）求证：对任意，．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．10、知函数（且）的图象经过点．（1）求函数的解析式；（2）设，用函数单调性的定义证明：函数在区间上单调递减．11、选修4-4：坐标系与参数方程已知函数是定义在上的奇函数，且．（1）求实数的值；（2）判断函数的单调性，并用定义证明；（3）解不等式：．12、已知函数，.（1）若函数在上不具有单调性，求实数的取值范围；（2）若.（ⅰ）求实数的值；（ⅱ）设，，，当时，试比较，，的大小．13、已知，当时，.（Ⅰ）若函数过点，求此时函数的解析式；（Ⅱ）若函数只有一个零点，求实数的值；（Ⅲ）设，若对任意实数，函数在上的最大值与最小值的差不大于1，求实数的取值范围.14、已知，函数．（1）当时，解不等式；（2）若关于的方程的解集中恰好有一个元素，求的取值范围；（3）设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围．15、已知，函数.（1）当时，解不等式；（2）若，不等式恒成立，求的取值范围；（3）若关于的方程的解集中恰好有一个元素，求的取值范围．16、设为奇函数，为常数．（1）求的值；（2）判断函数在上的单调性，并说明理由；（3）若对于区间上的每一个值，不等式恒成立，求实数的取值范围．17、已知函数（a为常数）是奇函数.（Ⅰ）求a的值与函数的定义域；（Ⅱ）若当时，恒成立．求实数的取值范围.18、已知．（1）若函数的值域为，求实数的取值范围；（2）若函数在区间上是增函数，求实数的取值范围．19、已知，求的值.20、已知．（1）当时，求的最小值；（2）当时，求的最小值.21、若不等式2x−log a x<0在x∈上恒成立，求实数a的取值范围．22、若a、b是方程2(lg x)2－lg x6＋3＝0的两个实根，求lg(ab)·(log a b＋log b a)的值．23、已知函数（1）判断f（x）的奇偶性并证明；（2）若f（x）的定义域为[α，β]（β＞α＞0），判断f（x）在定义域上的增减性，并加以证明；（3）若0＜m＜1，使f（x）的值域为[log m m（β﹣1），log m m（α﹣1）]的定义域区间[α，β]（β＞α＞0）是否存在？若存在，求出[α，β]，若不存在，请说明理由．（12分）24、已知函数．（I）当时，求函数的定义域；（II）若关于的不等式的解集是，求的取值范围．25、已知函数为奇函数.（1）求m的值，并求f (x)的定义域；（2）判断函数的单调性，不需要证明；（3）若对于任意,是否存在实数,使得不等式.若存在,求出实数的取值范围;若不存在,请说明理由.26、一般地，如果函数的图象关于点对称，那么对定义域内的任意，则恒成立，已知函数的定义域为，其图象关于点对称. （1）求常数的值；（2）解方程：；（3）求证：.27、已知是函数的图象上任意两点，且，点. （1）求的值；（2）若，，且，求；（3）已知，其中，为数列的前项和，若对一切都成立，试求的取值范围.28、已知函数, 函数．（1）若的定义域为，求实数的取值范围；（2）当时，求函数的最小值；（3）是否存在非负实数m、n,使得函数的定义域为，值域为，若存在，求出、的值；若不存在，则说明理由．29、已知函数f（x）=log a x（a＞0且a≠1）（1）当a=3时，求方程f（）f（3x）=﹣5的解；（2）若f（3a﹣1）＞f（a），求实数a的取值范围；（3）当a=时，设g（x）=f（x）﹣3x+4，求证：对任意λ＞0，都存在μ＞0，使得g（x）＜0对x∈（λμ，+∞）恒成立．30、已知函数（，）．（1）当时，讨论的奇偶性，并证明函数在上为单调递减；（2）当时，是否存在实数和，使得函数的值域为，若存在，求出实数与的值，若不存在，说明理由．31、已知函数．（1）若函数的定义域为R，求实数a的取值范围；（2）若函数的值域为（﹣∞，﹣1]，求实数a的取值范围；（3）若函数在区间上为增函数，求实数a的取值范围．32、设函数（且)是定义域为R的奇函数．（Ⅰ）求t的值；（Ⅱ）若函数的图象过点，是否存在正数m，使函数在上的最大值为0，若存在，求出m的值；若不存在，请说明理由．33、设函数其中．（Ⅰ）证明：是上的减函数；（Ⅱ）若，求的取值范围．34、已知函数．①当时，求函数的值域；②若A，函数在A内是增函数，求的取值范围．35、已知函数是偶函数．（1）求的值；（2）若函数的图象与直线没有交点，求的取值范围．（3）设，若函数的图象有且只有一个公共点，求实数的取值范围36、已知函数.（Ⅰ）求函数的定义域；（Ⅱ）判断函数的奇偶性；（Ⅲ）若，求的取值范围.37、（2015秋•郑州校级期末）已知函数，其反函数为y=g（x）．（Ⅰ）若g（mx2+2x+1）的定义域为R，求实数m的取值范围；（Ⅱ）当x∈[﹣1，1]时，求函数y=[f（x）]2﹣2af（x）+3的最小值h（a）；（Ⅲ）是否存在实数m＞n＞2，使得函数y=h（x）的定义域为[n，m]，值域为[n2，m2]，若存在，求出m、n的值；若不存在，则说明理由．38、若函数的定义域为．当时，求的最值及相应的的值．39、（2015•湘西州校级一模）已知函数f（x）=log a（1﹣x）+log a（x+3）（0＜a＜1）（1）求函数f（x）的定义域；（2）求函数f（x）的零点；（3）若函数f（x）的最小值为﹣4，求a的值．40、（1）已知，求的值；（2）．41、已知函数（）是偶函数．（1）求实数的值；（2）证明：对任意的实数，函数的图象与直线最多只有一个公共点；（3）设，若与的图象有且只有一个公共点，求实数的取值范围．42、已知函数的图象恒过定点，且点又在函数的图象上．（1）求实数的值；（2）解不等式；（3）函数的图象与直线有两个不同的交点时，求的取值范围．43、设．（1）求的值；（2）求的最小值．44、已知函数，当时，恒有．（1）求的表达式及定义域；（2）若方程有解，求实数的取值范围；（3）若方程的解集为，求实数的取值范围．45、有一种候鸟每年都按一定的路线迁陟，飞往繁殖地产卵．科学家经过测量发现候鸟的飞行速度可以表示为函数，单位是，其中表示候鸟每分钟耗氧量的单位数，表示测量过程中候鸟每分钟的耗氧偏差．（参考数据：，，）（1）若，候鸟每分钟的耗氧量为个单位时，它的飞行速度是多少？（2）若，候鸟停下休息时，它每分钟的耗氧量为多少个单位？（3）若雄鸟的飞行速度为，雌鸟的飞行速度为，那么此时雄鸟每分钟的耗氧量是雌鸟每分钟的耗氧量的多少倍？46、函数是奇函数．（1）求的值；（2）判断在区间上单调性并加以证明；47、已知函数，当点在函数的图象上运动时，点在函数（）的图象上运动．（1）求函数的解析式；（2）求函数的零点．（3）函数在上是否有最大值、最小值；若有，求出最大值、最小值；若没有请说明理由．48、已知函数，当点在函数的图象上运动时，点在函数（）的图象上运动．（1）求函数的解析式；（2）求函数的零点．（3）函数在上是否有最大值、最小值；若有，求出最大值、最小值；若没有请说明理由．49、设函数，函数，且，的图象过点及．（1）求和的表达式；（2）求函数的定义域和值域．50、已知函数．（1）讨论函数的单调性；（2）若对于任意的恒成立，求的范围．51、已知函数（，且）．（1）求函数的定义域和值域；（2）若函数有最小值为，求的值．52、选修不等式讲已知函数（1）当时，求函数的定义域；（2）若对任意的，都有成立，求实数的取值范围．53、已知函数在其定义域上为奇函数．（1）求的值；（2）若关于的不等式对任意实数恒成立，求实数的取值范围．54、已知函数．（1）判断并证明的奇偶性；（2）求证：；（3）已知，，且，，求，的值．55、（本小题满分12分）已知函数（Ⅰ）若1是关于x的方程的一个解，求t的值；（Ⅱ）当时，解不等式；（Ⅲ）若函数在区间上有零点，求t的取值范围．56、（本小题满分10分）已知函数（a＞0,且a≠1），=．（1）函数的图象恒过定点A，求A点坐标；（2）若函数的图像过点（2,），证明：方程在（1，2）上有唯一解．57、（本小题满分12分）已知函数（为常数）是奇函数．（Ⅰ）求的值；（Ⅱ）若当时，恒成立．求实数的取值范围．58、（本小题满分10分）已知函数（其中），﹒（1）若命题“”是真命题，求x的取值范围；（2）设命题p：，或，若是假命题，求m的取值范围﹒59、已知函数是偶函数，且在上单调递增．（1）求m的值，并确定的解析式；（2），求的定义域和值域。

对数资料（1） 对数与对数函数测试题一、 选择题： 1．已知3a=5b= A ，且a 1＋b1= 2，则A 的值是( )． (A)．15 (B)．15 (C)．±15 (D)．225 2．已知a ＞0，且10x= lg(10a)＋lga1，则x 的值是( )． (A)．－1 (B)．0 (C)．1 (D)．2 3．若x 1，x 2是方程lg 2x ＋(lg3＋lg2) lg x ＋lg3·lg2 = 0的两根，则x 1x 2的值是( )． (A)．lg3·lg2 (B)．lg6 (C)．6 (D)．61 4．若log a (a 2＋1)＜log a 2a ＜0，那么a 的取值范围是( )． (A)．(0，1) (B)．(0，21) (C)．(21，1) (D)．(1，＋∞) 5． 已知x =31log 121＋31log 151，则x 的值属于区间( )．(A)．(－2，－1) (B)．(1，2) (C)．(－3，－2) (D)．(2，3) 6．已知lga ，lgb 是方程2x 2－4x ＋1 = 0的两个根，则(lgba )2的值是( )． (A)．4 (B)．3 (C)．2 (D)．1 7．设a ，b ，c ∈R ，且3a= 4b= 6c，则( )． (A)．c 1=a 1＋b 1 (B)．c 2=a 2＋b 1 (C)．c 1=a 2＋b 2 (D)．c 2=a 1＋b2 8．已知函数y = log 5.0(ax 2＋2x ＋1)的值域为R ，则实数a 的取值范围是( )． (A)．0≤a ≤1 (B)．0＜a ≤1 (C)．a ≥1 (D)．a ＞1 9．已知lg2≈0.3010，且a = 27×811×510的位数是M ，则M 为( )．(A)．20 (B)．19 (C)．21 (D)．22 10．若log 7[ log 3( log 2x)] = 0，则x 21为( )．(A)．321 (B)．331 (C)．21 (D)．42 11．若0＜a ＜1，函数y = log a [1－(21)x]在定义域上是( )． (A)．增函数且y ＞0 (B)．增函数且y ＜0 (C)．减函数且y ＞0 (D)．减函数且y ＜012．已知不等式log a (1－21+x )＞0的解集是(－∞，－2)，则a 的取值范围是( )． (A)．0＜a ＜21 (B)．21＜a ＜1 (C)．0＜a ＜1 (D)．a ＞1 二、 填空题13．若lg2 = a ，lg3 = b ，则lg 54=_____________． 14．已知a = log 7.00.8，b = log 1.10.9，c = 1.19.0，则a ，b ，c 的大小关系是_______________．15．log12-(3＋22) = ____________．16．设函数)(x f = 2x(x ≤0)的反函数为y =)(1x f -，则函数y =)12(1--x f 的定义域为________．三、 解答题17．已知lgx = a ，lgy = b ，lgz = c ，且有a ＋b ＋c = 0，求xcb 11+·yac 11+·xba 11+的值．18．要使方程x 2＋px ＋q = 0的两根a 、b 满足lg(a ＋b) = lga ＋lgb ，试确定p 和q 应满足的关系． 19．设a ，b 为正数，且a 2－2ab －9b 2= 0，求lg(a 2＋ab －6b 2)－lg(a 2＋4ab ＋15b 2)的值． 20．已知log 2[ log 21( log 2x)] = log 3[ log 31( log 3y)] = log 5[ log 51( log 5z)] = 0，试比较x 、y 、z 的大小．21．已知a ＞1，)(x f = log a (a －a x)．⑴ 求)(x f 的定义域、值域； ⑵判断函数)(x f 的单调性 ，并证明； ⑶解不等式：)2(21--x f＞)(x f ．22．已知)(x f = log 21[ax2＋2(ab)x －bx2＋1]，其中a ＞0，b ＞0，求使)(x f ＜0的x 的取值范围．参考答案：一、选择题：1．(B)．2．(B)． 3．(D)．4．(C)．5．(D)．6．(C)．7．(B)．8．(A)． 9．(A)．10．(D)．11．(C)．12．(D)． 提示：1．∵3a＋5b= A ，∴a = log 3A ，b = log 5A ，∴a 1＋b1= log A 3＋log A 5 = log A 15 = 2，∴A =15，故选(B)．2．10x= lg(10 a)＋lga 1= lg(10a ·a1) = lg10 = 1，所以 x = 0，故选(B)． 3．由lg x 1＋lg x 2=－(lg3＋lg2)，即lg x 1x 2= lg 61，所以x 1x 2=61，故选(D)．4．∵当a ≠1时，a 2＋1＞2a ，所以0＜a ＜1，又log a 2a ＜0，∴2a ＞1，即a ＞21，综合得21＜a ＜1，所以选(C)． 5．x = log 3121＋log 3151= log 31(21×51) = log 31101= log 310，∵9＜10＜27，∴ 2＜log 310＜3，故选(D)．6．由已知lga ＋lgb = 2，lga ·lgb =21，又(lg ba )2= (lga －lgb)2= (lga ＋lgb)2－4lga ·lgb = 2，故选(C)．7．设3a= 4b= 6c= k ，则a = log 3k ，b= log 4k ，c = log 6k ，从而c 1= log k 6 = log k 3＋21log k 4 =a 1＋b 21，故c 2=a 2＋b1，所以选(B)． 8．由函数y = log 5.0(ax 2＋2x ＋1)的值域为R ，则函数u(x) = ax 2＋2x ＋1应取遍所有正实数，当a = 0时，u(x) = 2x ＋1在x ＞－21时能取遍所有正实数； 当a ≠0时，必有⎩⎨⎧≥-=∆.44,0a ＞a ⇒0＜a ≤1．所以0≤a ≤1，故选(A)．9．∵lga = lg(27×811×510) = 7lg2＋11lg8＋10lg5 = 7 lg2＋11×3lg2＋10(lg10－lg2) = 30lg2＋10≈19.03，∴a = 1003.19，即a 有20位，也就是M = 20，故选(A)．10．由于log 3( log 2x) = 1，则log 2x = 3，所以x = 8，因此 x 21-= 821-=81=221=42，故选(D)． 11．根据u(x) = (21)x 为减函数，而(21)x ＞0，即1－(21)x ＜1，所以y = log a [1－(21)x]在定义域上是减函数且y ＞0，故选(C)． 12．由－∞＜x ＜－2知，1－21+x ＞1，所以a ＞1，故选(D)． 二、填空题13．21a ＋23b 14．b ＜a ＜c ． 15．－2． 16．21＜x ≤1 提示： 13．lg 54=21lg(2×33) =21( lg2＋3lg3) =21a ＋23b ． 14．0＜a = log 7.00.8＜log 7.00.7 = 1，b = log 1.10.9＜0，c = 1.19.0＞1.10= 1，故b ＜a ＜c ．15．∵3＋22= (2＋1)2，而(2－1)(2＋1) = 1，即2＋1= (2－1)1-，∴log 12-(3＋22) =log 12-(2－1)2-=－2．16．)(1x f-= log 2x (0＜x ≤1＝，y =)12(1--x f 的定义域为0＜2x －1≤1，即21＜x ≤1为所求函数的定义域． 三。

数学必修一【对数函数同步】精练卷一、选择题1.已知对数函数y＝logax当a取不同值时对应的图像如图所示，已知a的值分别为，则相应于C1，C2，C3，C4的a值依次是()A. 431,,3510B.413,,3105C.431,3510D.413,31052.若f(x)＝121log(21)x+，则f(x)的定义域为()A.1(,0)2-B.1(,)2-+?C.1(,0)2-∪(0，＋∞) D.1(,2)2-3.已知0＜a＜1，b＞1，且ab＞1，则下列不等式中成立的是()A. logb 1b＜logab＜loga1b B. logab＜logb1b＜loga1bC. logab＜loga 1b＜logb1b D. logb1b＜loga1b＜logab4.若点(a,b)在lgy x=图像上，1a¹,则下列点也在此图像上的是A. （1a，b） B. (10a,1-b) C. (10a,b+1) D. (a2,2b)二、填空题5.若函数y＝(a2－3a＋3)logax是对数函数，则a的值为______．6.设f(x)是奇函数，当x＞0时，f(x)＝log2x，则当x＜0时，f(x)的表达式为_________________．7.若11log log44a a=，且|logba|＝－logba，则a，b满足的条件是________________．三、解答题8.求下列函数的定义域：(1)f(x)＝log(5－x)(2x －3)； (2)f(x)＝log2(3x －1)．9.画出函数y ＝log3x 的图像，并归纳出它的单调性及奇偶性．解析北师大版数学必修一【对数函数同步】精练卷一、选择题1.已知对数函数y ＝logax 当a 取不同值时对应的图像如图所示，已知a 的值分别为，则相应于C1，C2，C3，C4的a 值依次是( )A. 431,,3510B. 413,,3105C. 431,3510D. 413,3105【答案】A【解析】【分析】由题意结合对数函数的性质确定C1，C2，C3，C4的a 值即可.【详解】令1y =，如图所示，所得交点的横坐标即为4321,,,C C C C 的a 值，结合题意可知：4321a a a a <<<，则C1，C2，C3，C4的a431,,3510. 本题选择A 选项.【点睛】本题主要考查对数函数图像的识别，属于基础题.2.若f(x)＝121log (21)x + ，则f(x)的定义域为( ) A. 1(,0)2-B. 1(,)2-+?C. 1(,0)2-∪(0，＋∞)D. 1(,2)2-【答案】C【解析】【分析】由题意得到关于x 的不等式组，求解不等式组即可确定函数的定义域. 【详解】函数有意义，则：()12log 210210x x ì+?ïíï+>î，求解不等式可得f(x)的定义域为1,02骣琪-琪桫∪(0，＋∞).本题选择C 选项.【点睛】求函数的定义域，其实质就是以函数解析式有意义为准则，列出不等式或不等式组，然后求出它们的解集即可．3.已知0＜a ＜1，b ＞1，且ab ＞1，则下列不等式中成立的是( ) A. logb 1b ＜logab ＜loga 1b B. logab ＜logb 1b ＜loga 1b C. logab ＜loga 1b ＜logb 1b D. logb 1b ＜loga 1b ＜logab【答案】 B【解析】【分析】由题意结合对数函数的单调性确定所给的对数的大小即可.【详解】由1b >可知101b <<， 由于101,0a ba ，函数()log a f x x =单调递减，故11log log log 1a ab b a b <==-， 且11log 0log a b b b >>， 综上可得：11log log log a b a b b b <<. 本题选择B 选项.【点睛】本题主要考查对数函数的单调性，对数比较大小的方法等知识，意在考查学生的转化能力和计算求解能力.4.若点(a,b)在lg y x =图像上，1a ¹,则下列点也在此图像上的是A. （1a ，b ）B. (10a,1-b)C. (10a ,b+1) D. (a2,2b)【答案】D【解析】此题考查函数的方程知识因为(a,b)在lg y x =图像上，所以lg b a =。

高一数学对数函数经典练习题令狐采学一、选择题：（本题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1、已知32a =，那么33log 82log 6-用a 表示是（ ）A 、2a -B 、52a -C 、23(1)a a -+D 、23a a -2、2log (2)log log a a a M N M N -=+，则NM 的值为（ ）A 、41B 、4C 、1D 、4或13、已知221,0,0x y x y +=>>，且1log (1),log ,log 1y a a a x m n x+==-则等于（ ）A 、m n +B 、m n -C 、()12m n +D 、()12m n -4. 若x 1，x 2是方程lg 2x ＋(lg3＋lg2)lgx ＋lg3·lg2 = 0的两根，则x 1x 2的值是( )．(A)．lg3·lg2 (B)．lg6 (C)．6 (D)．61 5、已知732log [log (log )]0x =，那么12x -等于（ ） A 、13B 、123C 、122D 、1336．已知lg2=a ，lg3=b ，则15lg 12lg 等于（ ）A ．ba ba +++12 B ．b a ba +++12 C ．ba ba +-+12 D ．ba b a +-+127、函数(21)log 32x y x -=- ） A 、()2,11,3⎛⎫+∞⎪⎝⎭B 、()1,11,2⎛⎫+∞⎪⎝⎭C 、2,3⎛⎫+∞⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是（ ）A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞9、若log 9log 90m n <<，那么,m n 满足的条件是（ ） A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<< 10、2log 13a <，则a 的取值范围是（ ）A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭C 、2,13⎛⎫⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中，在()0,2上为增函数的是（ ） A 、12log (1)y x =+B 、22log 1y x =-C 、21log y x=D 、22log (45)y x x =-+12．已知函数y=log 21 (ax2＋2x ＋1)的值域为R ，则实数a 的取值范围是（ ）A ．a ＞ 1B ．0≤a＜ 1C ．0＜a ＜ 1D ．0≤a≤1二、填空题：（本题共4小题，每小题4分，共16分，请把答案填写在答题纸上） 13计算：log2.56.25＋lg1001＋ln e ＋3log 122+= ．14、函数(-1)log (3-)x y x =的定义域是。

高中数学对数函数经典练习题及答案（优秀4篇）对数函数练习题篇一一、选择题1、下列函数(1)y= x (2)y=2x-1 (3)y=1x (4)y=2-1-3x (5)y=x2-1中，是一次函数的有( )A.4个B.3个C.2个D.1个2、A 、B(x2,y2)是一次函数y=kx+2(k>0)图像上的不同的两点，若则( )A.t0 C.t>1 D. t≤13、直线y=x-1与坐标轴交于A、B两点，点C在坐标轴上，△ABC为等腰三角形，则满足条件的三角形最多有( )A. 5个B.6个C.7个D.8个4、把直线y=﹣x+3向上平移m个单位后，与直线y=2x+4的交点在第一象限，则m的取值范围是( )A.11 D.m0的解集是( )A.x>3B.-2-29.一次函数y=ax+1与y=bx-2的图象交于x轴上一点，那么a:b等于( )A. B.C. D.以上答案都不对10、函数y=kx+b，那么当y>1时，x的取值范围是：( )A、x>0B、x>2C、x212、在平面直角坐标系中，线段AB的端点A(-2，4),B(4，2),直线y=kx-2与线段AB有交点，则k的值不可能是( )A.5B.-5C.-2D.3二、填空题13、如果直线y = -2x+k与两坐标轴所围成的三角形面积是9，则k的值为_____.14、平面直角坐标系中，点A的坐标是(4，0)，点P在直线y=-x+m上，且AP=OP=4.则m的值是。

15、直线y=kx+2经过点(1,4),则这条直线关于x轴对称的直线解析式为：。

16、已知一条直线经过点A(0，2)、点B(1，0)，将这条直线向左平移与x 轴、y轴分别交与点C、点D.若DB=DC，则直线CD的函数解析式为 .17、点A的坐标为(-2，0)，点B在直线y=x-4上运动，当线段AB最短时，点B的坐标是___________。

18、已知三个一次函数y1=x,y2= x+1,y3=- x+5。

对数函数练习题及答案一、选择题：1. 函数y=log_{2}x的定义域是：A. (0, +∞)B. (-∞, 0)C. (-∞, +∞)D. [0, +∞)2. 若log_{3}9=2，则log_{3}3的值为：A. 1B. 2C. 3D. 93. 函数y=log_{10}x的值域是：A. (-∞, 0)B. (-∞, 1]C. (0, +∞)D. R4. 以下哪个等式是正确的？A. log_{a}a=1B. log_{a}1=0C. log_{a}a^2=2D. 所有选项都正确5. 若log_{5}25=b，则b的值为：A. 2B. 5C. 25D. 125二、填空题：1. 函数y=log_{x}e的值域为______。

2. 若log_{2}8=3，则2^{3}=______。

3. 对于函数y=log_{a}x，当a>1时，函数在(0,+∞)上是______的。

4. 根据对数的定义，log_{10}100=______。

5. 若log_{4}16=2，则4^{2}=______。

三、解答题：1. 求函数y=log_{4}x的反函数，并证明其正确性。

2. 已知log_{3}27=3，求log_{9}3。

3. 证明：对于任意正数a>1，log_{a}1=0。

4. 已知log_{2}32=5，求2^{5}的值。

5. 已知函数f(x)=log_{a}x，求f(a)的值，并讨论a的取值范围。

四、应用题：1. 某工厂的产量每年以相同的比率增长，如果第一年的产量是100吨，第二年的产量是121吨，求第三年的产量。

2. 某药物的半衰期是4小时，如果初始剂量是100毫克，4小时后剩余多少？3. 某城市的人口增长率是每年2%，如果当前人口是100万，求5年后的人口。

答案：一、选择题：1. A2. A3. D4. D5. A二、填空题：1. (0, +∞)2. 83. 增4. 25. 16三、解答题：1. 反函数为x=4^y，证明略。

可编辑修改精选全文完整版对数函数一、选择题1.设0.32a =,20.3b =,2log 0.3c =,则,,a b c 的大小关系( )A. a b c <<B. b c a <<C. c b a <<D. c a b <<2.已知0.1 1.32log 0.3,2,0.2a b c ===，则,,a b c 的大小关系是（ ） A ．a b c << B ．c a b << C ．a c b << D ．b c a <<3.式子25123lg lg lg +-= ( )A.2B.1C.0D.﹣24.使式子 2(1)log (1)x x -- 有意义的 x 的值是（ ）A. 1x <- 或 1x >B. 1x > 且 2x ≠C. 1x >D. 2x ≠5.函数()()22log 23f x x x =+-的定义域是( )A. []3,1-B. ()3,1-C. (][),31,-∞-⋃+∞D. (,3)(1,)-∞-⋃+∞6.已知0a >,且1a ≠,函数x y a =与log ()a y x =-的图像只能是图中的( ) A. B. C. D.7.函数()2()ln 28f x x x =--的单调递增区间是( )A. (),2-∞-B. (),1-∞C. ()1,+∞D. ()4,+∞ 8.函数()()20.5f log 2x x x =-++的单调递增区间为( ) A. 11,2⎛⎫- ⎪⎝⎭ B. 1,22⎛⎫ ⎪⎝⎭ C. 1,2⎛⎫+∞ ⎪⎝⎭ D.前三个答案都不对二、填空题9.计算: =-⨯5log 3132log 9log 125278__________.10.计算: 4413log 3log 32⨯=__________.11.如图所示的曲线是对数函数log a y x =当a 取4个不同值时的图像,已知a 的值分别为4313,,,3510,则相应于1234,,,C C C C 的a 值依次为__________.12.函数()()log 21a f x x =--(0,)a a >≠的图像恒过定点__________.13.函数()log 23a y x =++ (0a >且1a ≠)的图像过定点__________.14.若3436x y ==,则21 x y+=__________. 15.已知()()0.450.45log 2log 1x x +>-,则实数x 的取值范围是______.三、解答题16.解不等式: ()()2log 4log 2a a x x ->-.17. 求函数()22log 65y x x =-+的定义域和值域.18.求函数212log (32)y x x =+-的值域.19.已知()()4log 41x f x =-.1.求()f x 的定义域;2.讨论()f x 的单调性;3.求()f x 在区间1,22⎡⎤⎢⎥⎣⎦上的值域.20.已知指数函数()(0,1)x f x a a a =>≠且.(1)写出()f x 的反函数()g x 的解析式；(2)解不等式()log (23)a g x x ≤-参考答案1.答案：C解析：因为1a >,01b <<,0c <,所以c b a <<,故选C.2.答案：C解析：由对数和指数的性质可知，∵2log 0.30a =<，0.10221b =>=，1.300.20.21c =<=，∴a c b <<.3.答案：A解析：4.答案：B解析：由 210{1011x x x ->->-≠,解得 1x > 且 2x ≠. 5.答案：D解析：由题意,得2230x x +->,事实上,这是个一元二次不等式,此处,我们有两种解决方法:一是利用函数223y x x =+-的图像观察得到,要求图像正确、严谨;二是利用符号法则,即2230x x +->可因式分解为()()310x x +⋅->,则30,{10x x +>->或30,{10,x x +<-<解得1x >或3x <-, 所以函数()f x 的定义域为(,3)(1,)-∞-⋃+∞.6.答案：B解析：可以从图象所在的位置及单调性来判别.也可以利用函数的性质识别图象,特别注意底数a 对图象的影响。

高一数学 对数与对数函数练习题一、选择题1．若1)(log log 23=x ，则x 等于（ ）A ．2B ．81 C ．8 D ．21 2．方程4123log =x 的解是（ ） A ．91=x B ．33=x C ．3=x D ．9=x3．已知n m a a ==3log ,2log ，则n m a +2＝（ ）A ．5B ．7C ．10D ．124．化简：31log 43log 4)3(log 2222++-，得（ ） A ．2B ．3log 222-C ．－2D ．23log 22-5．计算：81log 16log 89⋅的值为（ ）A ．18B ．181C ．38D ．836．函数x x x f -+-=4)1lg()(的定义域为（ ）A ．]4,1(B ．（1,4）C ．［1,4］D ．)4,1[7．在同一坐标系中，函数x y 3log =与x y 31log =的图象之间的关系是（ ）A ．关于y 轴对称B ．关于x 轴对称C ．关于原点对称D ．关于直线x y =对称8．函数|log |2x y =的图象是图中的（ ）9．若函数)(log )(b x x f a +=的图象如图，其中b a ,为常数，则函数b a x g x +=)(的图象大致是（ ）10．若集合}21log |{21≥=x x A ，则A C R 等于（ ）A ．),22(]0,(+∞-∞Y B ．),22(+∞ C ．),22[]0,(+∞-∞Y D ．),22[+∞ 11．设2log ,3log ,log 323===c b a π，则（ ）A ．c b a >>B ．b c a >>C ．c a b >>D ．a c b >>12．函数)11lg()(2xx x f ++=的奇偶性是（ ）A ．奇函数B ．偶函数C ．即奇又偶函数D ．非奇非偶函数13．函数)124(log 231++-=x x y 的单调递减区间是（ ）A ．)2,(-∞B ．),2(+∞C ．（－2,2）D ．（－2,6）14．设14log ,10log ,6log 753===c b a ，则（ ）A ．a b c >>B ．a c b >>C ．b c a >>D ．c b a >>15．已知函数)(x f 是定义在R 上的偶函数，且在区间),0[+∞上单调递增，若实数a 满足)1(2)(log )(log 212f a f a f ≤+，则a 的取值范围是（ ）A ．]2,1[B ．]21,0(C ．]2,21[D ．]2,0( 16．化简)2log 2)(log 3log 3(log 9384++＝ .17．若b a ==3lg ,2lg ，则12log 5等于.18．设函数)10(log )(≠>=a a x x f a 且，若8)(201421=⋅⋅⋅x x x f ，则)()()(220142221x f x f x f +⋅⋅⋅++的值等于.19．已知定义域为R 的偶函数)(x f 在),0[+∞上是增函数，且0)21(=f ，则不等式0)(log 4<x f 的解集是.20．已知函数⎩⎨⎧>≤--=,1,log ,1,1)2()(x x x x a x f a若)(x f 在),(+∞-∞上单调递增，则实数a的取值范围为.21．计算：（1）)223(log 29log 2log 3777+-.（2）25lg 50lg 2lg )2(lg 2+⋅+.22．已知x 满足不等式：03log 7)(log 221221≤++x x ，求函数)2(log )4(log )(22xx x f ⋅=的最大值和最小值.。

高一数学对数函数 同步练习一．选择题1、 下列各函数中，在()2,0上为增函数的是 A ．()2log 5.0+=x y B ．1log 22-=x yC ．xy 1log 3=D ．()54log 25.0+-=x x y2、 已知函数()()12log 12+=-x y a 在⎪⎭⎫⎝⎛-0,21内恒有0>y ，那么a 的取值范围是 A ．1>a B ．10<<a C ．11>-<a a 或 D ．2112<<-<<-a a 或3、 函数()1lg +=x y 的单调性为 A ．在()+∞∞-,增B ．在()+∞∞-,减C ．在()+∞,0增D ．在()+∞,0减4、 函数()25.045log x x y -+=的递增区间是A ．()2,∞-B ．()∞+,2C ．()2,1-D ．()5,25、 若函数()202lg 2+-=x x y 的定义域为[]10,0，则它的值域为A ．[]2,2lg 1+B ．[]2,19lgC ．[]10,2lg 1+D ．[]10,19lg6、 若函数x y 5.0log 2=的值域为[]1,1-，则它的定义域为A ．⎥⎦⎤⎢⎣⎡2,22 B ．⎥⎦⎤⎢⎣⎡2,21 C ．[]1,1- D ．[)+∞⎥⎦⎤ ⎝⎛∞-,222,7、 已知函数()x x f lg =，b a <<0，且()()b f a f >，则 A ．1>abB ．1=abC ．1<abD ．1<b8、 方程()xx 34log 2=+的实根个数为 A ．0B ．1C ．2D ．3二．填空题1、函数()x x f a log =在区间[]π,2上的最大值比最小值大1，则=a．2、若函数()x f 与xy 2=的图象关于直线x y =对称，则函数()1522++-=x x f y 的递减区间是 ． 3、当⎪⎭⎫ ⎝⎛∈21,0x 时，函数()x x y a a log log 2+-=有意义，则实数∈a ．4、已知函数()a x x y +-=4log 22，设方程042=+-a x x 的判别式为∆，（1）若3=a ，则∆ 0；函数的定义域是 ；值域是 ． （2）若4=a ，则∆ 0；函数的定义域是 ；值域是 ． （3）若5=a ，则∆ 0；函数的定义域是 ；值域是 ．（4）若函数定义域为R ，则实数∈a；若函数值域为R ，则实数∈a ． 三．解答题1、 已知()()41,log 12≤≤+=x x x f ，求函数()()()22x f x f x g +=的最大值与最小值．2、 已知函数()11010+=xxx f ，求()x f 1-并判断()x f 1-的单调性．3、已知()x x f a log =在[)+∞,3上恒有()1>x f ，求a 的取值范围．参考答案一． 选择题 DDCD BACC 二．填空题1、2π或π2． 2、[)5,1． 3、⎪⎭⎫⎢⎣⎡1,161． 4、（1）>、()()∞+∞-,31, 、R ； （2）=、()()∞+∞-,22, 、R ；（3）<、 R 、 [)∞+,0； （4）()∞+,4、(]4,∞-．三．解答题 1、 解：设()21log 2≤≤=x x t ，则[]1,0∈t ，（注意()2x f 的定义域）∵=y ()()()22x f x f x g +=x x x 2222log 211log 2log ++++=242++=t t []1,0∈t ，∴()x g的最大值是7，最小值是2．2、 解：由11010+=xx y 解得y y x -=110， ∵010>x，∴10<<y ； 于是：()xxx f-=-1lg1，()1,0∈x ． 当1021<<<x x 时，()()212122111111x x x x x x x x ---=---∵011>-x ，012>-x ，021<-x x ，∴221111x x x x -<-，于是：22111lg 1lg x xx x -<-，即：()()2111x fx f--<．∴()x f 1-在()1,0上是增函数．3、解： 当1>a 时，∵[)+∞∈,3x ，∴()0log >==x x f y a ，由()1>x f ，得a x a a log 1log =>，∴x a <对任意[)+∞∈,3x 恒成立．于是：31<<a ．当10<<a 时，∵[)+∞∈,3x ，∴()0log <==x x f y a ，由()1>x f ，得a x x a aa log 11log log =>=-，∴xa 1>对任意[)+∞∈,3x 恒成立． 于是：131<<a ．综之：()3,11,31 ⎪⎭⎫⎝⎛∈a。

高一数学对数函数练习题1. 计算对数函数 \(\log_2 8\) 的值。

2. 求解方程 \(\log_3 x = 2\) 中的 \(x\) 值。

3. 已知 \(\log_5 25 = b\)，求 \(5^b\) 的值。

4. 判断下列对数函数的增减性：- \(y = \log_2 x\)- \(y = \log_{1/2} x\)5. 利用对数的性质，化简表达式 \(\log_3 9 + \log_3 3\)。

6. 将对数方程 \(\log_2 x = \log_3 9\) 转换为指数形式。

7. 计算 \(\log_{10} 1000\) 的值，并说明其意义。

8. 已知 \(a = \log_2 8\) 和 \(b = \log_3 27\)，求 \(a + b\) 的值。

9. 判断函数 \(y = \log_2 (x-1)\) 的定义域。

10. 解不等式 \(\log_2 x > 1\) 并给出解集。

11. 利用换底公式计算 \(\log_5 7\) 的近似值。

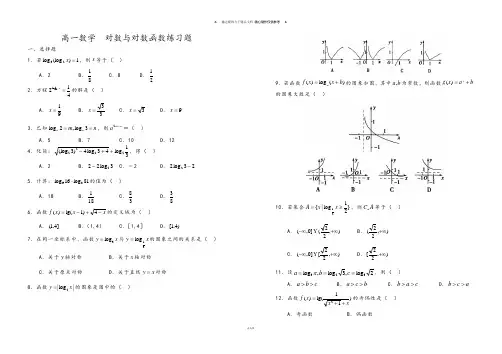
12. 已知 \(\log_2 3 = m\)，求 \(\log_3 8\) 的值。

13. 判断函数 \(y = \log_2 x\) 的图像是否关于直线 \(y = x\) 对称。

14. 计算 \(\log_2 32 - \log_2 8\) 的值。

15. 已知 \(\log_3 x = 1\)，求 \(x\) 的值。

16. 利用对数的性质，化简表达式 \(\log_2 64 - 2\log_2 4\)。

17. 解方程 \(\log_4 x + \log_4 (x-1) = 2\) 并给出解集。

18. 判断函数 \(y = \log_{1/3} x\) 的图像是否经过点 \((1,0)\)。

19. 计算 \(\log_{1/2} 1/8\) 的值，并说明其意义。

20. 已知 \(\log_2 5 = a\) 和 \(\log_2 10 = b\)，求 \(\log_250\) 的值。

2.2.1 对数与对数的运算练习一一、选择题1、 25)(log 5a -（a ≠0）化简得结果是（ ） A 、－a B 、a 2C 、｜a ｜D 、a2、 log 7［log 3（log 2x ）］＝0，则21-x等于（ ） A 、31B 、321C 、221D 、331 3、 n n ++1log （n n －＋1）等于（ ）A 、1B 、－1C 、2D 、－24、 已知32a =，那么33log 82log 6-用表示是（ ）A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a -5、 2log (2)log log a a a M N M N -=+，则N M 的值为（ ） A 、41 B 、4 C 、1 D 、4或1 6、 若log m 9<log n 9<0,那么m,n 满足的条件是（ ）A 、m>n>1B 、n>m>1C 、0<n<m<1D 、0<m<n<17、 若1<x<b,a=log ２b x,c=log a x,则a,b,c 的关系是（ ）A 、a<b<cB 、 a<c<bC 、c<b<aD 、c<a<b二、填空题8、 若log a x ＝log b y ＝－21log c 2，a ，b ，c 均为不等于1的正数，且x ＞0，y ＞0，c ＝ab ，则xy ＝________ 9 、若lg2＝a ，lg3＝b ，则log 512＝________10、 3a ＝2，则log 38－2log 36＝__________11、 若2log 2,log 3,m n a a m n a+===___________________ 12、 lg25+lg2lg50+(lg2)2=三、解答题13、 222522122(lg )lg lg (lg )lg +⋅+-+ 14、 若lga 、lgb 是方程01422=+-x x 的两个实根，求2)(lg )lg(b a ab ⋅的值。

新高一对数测试题及答案一、选择题（每题5分，共30分）1. 对数函数y=log_a x（a>0且a≠1）的图像不经过第几象限？A. 第一象限B. 第二象限C. 第三象限D. 第四象限2. 已知log_a b = c，那么a^c等于多少？A. bB. cC. aD. b^c3. 计算log_2 8的值是多少？A. 2B. 3C. 4D. 54. 如果log_a b = log_c b，那么a和c的关系是什么？A. a = cB. a = 1/cC. a = c^(-1)D. a = b^(-1)5. 以下哪个表达式是正确的？A. log_a (a^x) = xB. log_a (a^x) = x/aC. log_a (a^x) = a^xD. log_a (a^x) = 1/x6. 已知log_3 9 = 2，那么log_3 3是多少？A. 1B. 2C. 3D. 4二、填空题（每题5分，共20分）1. 计算log_5 25的值是______。

2. 如果log_2 4 = 2，那么2^log_2 4 = ______。

3. 已知log_10 100 = 2，那么log_10 0.01 = ______。

4. 计算log_2 (2^3)的值是______。

三、解答题（每题10分，共50分）1. 已知log_3 27 = 3，求log_3 3^3。

2. 计算log_4 64的值，并将其转换为以2为底的对数。

3. 已知log_2 8 = 3，求2^(log_2 8)的值。

4. 已知log_5 25 = 2，求5^(log_5 25)的值。

5. 计算log_2 (32 * 8)的值，并将其转换为以10为底的对数。

答案：一、选择题1. D2. A3. B4. C5. A6. A二、填空题1. 22. 43. -24. 3三、解答题1. 32. 3，转换为以2为底的对数为log_2 64 = 63. 84. 255. 6，转换为以10为底的对数为log_10 (32 * 8) = log_10 256 = 2.4。

1已知集合M ＝{0,1,2}，N ＝{x |x ＝－a ，a ∈M }，则集合M ∩N ＝( ) A ．{0，－1} B ．{0}C ．{－1，－2} D ．{0，－2} 2集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}． (1)若B ⊆A ，求实数m 的取值范围； (2)当x ∈Z 时，求A 的非空真子集的个数；(3)当x ∈R 时，若A ∩B ＝∅，求实数m 的取值范围． 3 已知函数f (x )＝lg(x ＋3)的定义域为M ，g (x )＝12－x的定义域为N ，则M ∩N 等于( ) A ．{x |x >－3} B ．{x |－3<x <2}C ．{x |x <2} D ．{x |－3<x ≤2} 4．下列各组函数中表示同一函数的是( ) A ．f (x )＝x 与g (x )＝()x 2B ．f (x )＝|x |与g (x )＝3x 3 C ．f (x )＝lne x与g (x )＝e ln x D ．f (x )＝x 2－1x －1与g (t )＝t ＋1(t ≠1) 5．已知f (2x ＋1)＝3x －4，f (a )＝4，则a ＝________.6已知函数f (x )＝⎩⎪⎨⎪⎧2x ，x >0，x ＋1，x ≤0，若f (a )＋f (1)＝0，则实数a 的值等于( )A ．－3B ．－1C ．1D ．37 下列函数中，既是偶函数又在(0，＋∞)上单调递增的函数是( ) A ．y ＝x 3 B ．y ＝|x |＋1C ．y ＝－x 2＋1 D ．y ＝2－|x |8．已知函数f (x )为R 上的减函数，则满足f ⎝⎛⎭⎫⎪⎪⎪⎪1x <f (1)的实数x 的取值范围是( ) A ．(－1,1) B ．(0,1)C ．(－1,0)∪(0,1) D ．(－∞，－1)∪(1，＋∞)9函数y ＝⎩⎪⎨⎪⎧3x ，x ∈(－∞，1)，log 2x ，x ∈[1，＋∞)的值域为( )A ．(0,3)B ．[0,3]C ．(－∞，3]D ．[0，＋∞) 10．函数f (x )＝ln(4＋3x －x 2)的单调递减区间是( ) A.⎣⎡⎭⎫32，4 B.⎝⎛⎦⎤12，4C.⎝⎛⎦⎤1，52 D.⎝⎛⎭⎫32，2 11函数f (x )＝a x ＋log a (x ＋1)在[0,1]上的最大值与最小值之和为a ，则a 的值是( ) A ．2 B.12C ．4 D.1412．已知f (x )＝ax 2＋bx 是定义在[a －1,2a ]上的偶函数，那么a ＋b 的值是( ) A ．－13 B.13 C.12 D ．－1213设f (x )为定义在R 上的奇函数．当x ≥0时，f (x )＝2x ＋2x ＋b (b 为常数)，则f (－1)＝( )A ．3B ．1C ．－1D ．－314 已知定义域为R 的偶函数f (x )在(－∞，0]上是减函数，且f ⎝⎛⎭⎫12＝0，则不等式f (log 2x )>0的解集为( )A.⎝⎛⎭⎫0，22∪(2，＋∞) B ．(2，＋∞)C.⎝⎛⎭⎫0，12∪(2，＋∞) D.⎝⎛⎭⎫0，12 15．计算：(log 25)2－4log 25＋4＋log 215＝________.15若函数y ＝log a (x ＋b )(a >0且a ≠1)的图象过两点(－1,0)和(0,1)，则( ) A ．a ＝2，b ＝2 B ．a ＝2，b ＝2C ．a ＝2，b ＝1 D ．a ＝2，b ＝ 2 16 函数f (x )＝log 2(3x ＋1)的值域为( )A ．(0，＋∞)B ．[0，＋∞)C ．(1，＋∞)D ．[1，＋∞)17 已知函数f (x )＝a x (a >0，a ≠1)是定义在R 上的单调递减函数，则函数g (x )＝log a (x ＋1)的图象大致是( )18．log 225·log 322·log 59＝( )A ．3 B ．4C ．5 D ．6 19 函数f (x )＝lg ⎝⎛⎭⎫21－x －1的图象关于( )A ．y 轴对称B ．直线x ＝1对称C ．点(1,0)对称D ．原点对称 20．若函数f (x )＝x 2＋2x ＋3a 没有零点，则实数a 的取值范围是( )A ．a ＜13B ．a ＞13C ．a ≤13D ．a ≥1321．不等式282144x x --⎛⎫> ⎪⎝⎭的解集为________________．23、已知32a=，那么33log 82log 6-用a 表示是（ ）A 、2a -B 、52a -C 、23(1)a a -+ D 、 23a a - 9、 将函数f x x()=2的图象向_________平移________个单位，就可以得到函数g x x ()=-22的图象。

对数函数（选择题：困难）
1、（2015秋•友谊县校级期末）已知，则=（）A． B．﹣8 C．4 D．8
2、若实数，满足，则关于的函数的图象大致形状是（）
3、已知函数，若存在实数，，，，满足，且
，则的取值范围是（）
A． B． C． D．
参考答案
1、C
2、B
3、B
【解析】
1、试题分析：直接利用否定函数求解函数值即可．
解：，
则=log3+=﹣2+6=4．
故选：C．
考点：对数的运算性质；函数的值．
2、试题分析：原式化为，两边取指数得：得：，所以图形大致是：关于
对称的两边随轴的延伸，无限接近的图形，故选B．
考点：1、函数的图象；2、函数的定义域、值域．
【方法点睛】本题通过函数图像主要考查函数定义域、值域及单调性、对称性，属于中档题．识别函数图象应注意以下几点：①函数的定义域、值域；②函数的性质（单调性、奇偶性、周期性等）；③函数图象上的特殊点（与坐标轴的交点、经过的定点等）；④对于给定函数的图象，要能从图象的左右、上下分布范围、趋势、对称性等方面研究函数．
3、试题分析:在平面直角坐标系中，作出函数的图象如图所示：
因为存在实数，，，，满足，且，所以由图象知：，，，，当时，直线与函数的图象有个交点，直线越往上平移，的值越小，直线直线越往下平移，的值越大，因为当时，，当时，
，所以的取值范围是，故选B．
考点：函数的图象．。