定积分的概念和性质公式

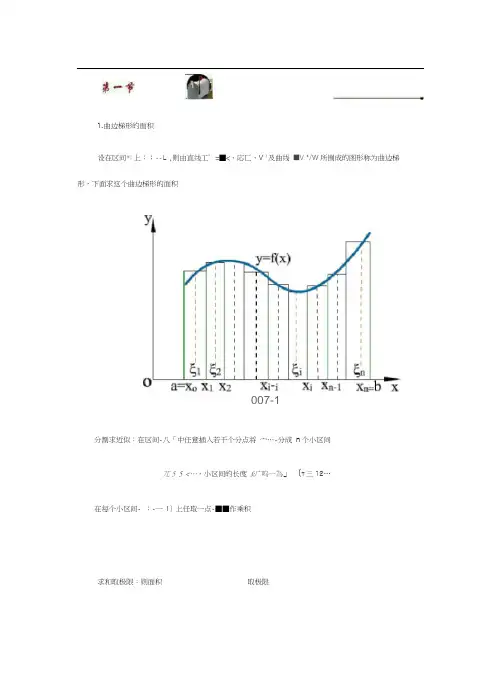
1.曲边梯形的面积设在区间*I上：；--L ,则由直线工’=■<、応匚、V 1及曲线■V °/W所围成的图形称为曲边梯形，下面求这个曲边梯形的面积分割求近似：在区间-八「中任意插入若干个分点将宀…-分成n个小区间兀5 5 <…，小区间的长度&广呜一為」（T三12…在每个小区间- ：-一I〕上任取一点-■■作乘积求和取极限：则面积取极限J=1其中；'1 ； J L厂V '…，即小区间长度最大者趋于零。

2.变速直线运动的路程设某物体作变速直线运动，速度| I「是上*的连续函数，且1■求在这段时间内物体所经过的路程。

分割求近似：在「〔[内插入若干分点■- _ "将其分成n 个小区间「—，小区间长度■- _■'.-1, ■1丄。

任取• _ _做求和取极限：则路程一取极限将分成n个小区间-，其长度为2 - —，在每个小区间上任取一点「:，作乘积■- ' ■'，并求和 r ，记1■r 1，如果不论对怎样分法，也不论小区间[:■ 上的点「怎样取法，只要当「「I;时，和总趋于确定的极限，则称这个极限为函数-—I在区间上的定积分，记作J '，即定义设函数」•、在L•二上有界，在-亠二中任意插入若干个分点其中叫被积函数，一’，八叫被积表达式，'‘叫积分变量，二叫积分下限, 「叫积分上限，-’」叫积分区间。

■叫积分和式。

说明：1.如果（*）式右边极限存在，称-’’」在区间-仁丄可积，下面两类函数在区间上…-可积，（1）」在区间-LL■- - 上连续，则■' J'-在可积。

（2）-’八在区间-‘丄-上有界且只有有限个间断点，则在--"-■ 上可积。

2.由定义可知，定积分的值只与被积函数和积分区间有关，而与积分变量无关，所3.在-上一，••——时，j ■表示曲线」、两条直线=<■ > - =■:与T轴所围成的曲边梯形的面积；在’1上「I时，V表示曲线，一―、两条直线、■-L ［与工'轴所围成的曲边梯形的面积（此时，曲边梯形在k轴的下方）；例1利用定积分的几何意义写出下列积分值(1)12（三角形面积）（2妇評（半圆面积）S7-2yiy|设-■■■可积性质1 J[[/⑴土畧（胡必=[f如± [畑賈性质2 J[灯■（力缶=斤£/（对乂性质3（定积分对区间的可加性）对任何三个不同的数,有性质5如果在区间上]…「，则J'"推论性质6 (定积分的估值) 设M及m分别是函数在区间一上的最大值及最小值，则~a) i［/(x)必~ a)性质7 (定积分中值定理)如果函数一、八在区间-上连续，则在"圖上至少有一点：，使「—■ C •.成立17-7例2比较下面两个积分的大小在(0, 1 )内，-'' '一"'-■单调增当兀［0」］时，有=6^ 2/(0) = 0，即尹m2-]的值&、令1 ,得‘‘由性质5,例3估计积分J 1解 只需求出’在区间-上的最大值、最小值即可。

定积分公式大全定积分是微积分中的重要概念，它在数学和物理学中都有着广泛的应用。

本文将介绍定积分的基本概念和常见的定积分公式，帮助读者更好地理解和运用定积分。

1. 定积分的基本概念。

定积分是微积分中的一个重要概念，它可以用来计算曲线下面的面积、求解曲线的弧长、计算物体的质量和质心等。

在几何学中，定积分可以用来计算曲线与坐标轴之间的面积；在物理学中，定积分可以用来描述物体的质量、质心和转动惯量等。

2. 定积分的基本性质。

定积分具有一些基本的性质，包括线性性、区间可加性和保号性等。

其中，线性性是指定积分对于常数的线性性质，即∫[a, b] (cf(x) + g(x))dx = c∫[a, b] f(x)dx + ∫[a, b] g(x)dx；区间可加性是指定积分在区间上的可加性质，即∫[a, b] f(x)dx + ∫[b, c] f(x)dx = ∫[a, c] f(x)dx；保号性是指定积分的结果与被积函数的正负性有关，即若f(x)在[a, b]上非负，则∫[a, b] f(x)dx ≥ 0。

3. 定积分的常见公式。

在定积分的计算中，有一些常见的定积分公式可以帮助我们简化计算过程，如换元积分法、分部积分法、定积分的性质公式等。

（1）换元积分法。

换元积分法是定积分中常用的一种积分方法，它通过引入新的变量来简化被积函数的形式，从而使积分计算更加容易。

换元积分法的基本思想是利用复合函数的求导和积分的性质，通过代换变量来简化被积函数的形式，然后进行积分计算。

（2）分部积分法。

分部积分法是定积分中另一种常用的积分方法，它通过对被积函数进行分解，然后利用积分的性质进行计算。

分部积分法的基本思想是利用积分的乘积法则，将被积函数进行分解，然后利用分部积分公式进行积分计算。

（3）定积分的性质公式。

定积分具有一些常见的性质公式，如定积分的线性性质、定积分的区间可加性和保号性等。

这些性质公式在定积分的计算中经常被使用，可以帮助我们简化积分的计算过程，提高计算的效率。

定积分的基本概念
一、定积分的基本概念
1.定积分的定义
定积分是指在区间[a,b]中，用函数f(x)的值在x处取的积分，其中x取值于a到b之间的某个点，f(x)的积分称为定积分。

也可以表示为
∫a, bf(x)dx=∫f(x)dx
即：将函数f(x)从x=a到x=b的定积分。

2.定积分的性质
（1）定积分是一种积分的形式，它是在定的一段区间内对某个函数f(x)求积分的形式。

（2）定积分可以表示为：∫f(x)dx=F(b)-F(a)，其中F(x)是f(x)的积分函数。

（3）定积分可以表示为：∫a, bf(x)dx=∑[f(x1)+f(x2)+…
+f(xn)]，其中x1,x2,…,xn为积分区间[a, b]的各个各点。

（4）定积分是一种表示曲线与坐标轴围成的面积的一种数学工具。

二、定积分的计算
1.定积分的数值计算
数值计算定积分，即把范围[a,b]离散成一定的小段，在每个小段上求f(x)的值，再用这些值进行总和，来求出定积分的近似值。

2.定积分的解析计算
解析计算此类定积分，即首先求出f(x)的积分方程，在范围[a,b]内，求得它的解后，再把范围[a,b]的定积分解析成积分函数F(x)的量对应的差值F(b)-F(a)。

三、定积分的应用
定积分的应用主要是用于求出曲线与坐标轴围成的面积，也可以用于求求解线性微分方程，求解有关动力学问题的时候，还有一些物理的和化学的问题，这些问题用的都是定积分的知识。

第二节定积分计算公式和性质一、变上限函数设函数在区间上连续，并且设x为上的任一点，于是，在区间上的定积分为这里x既是积分上限，又是积分变量，由于定积分与积分变量无关，故可将此改为如果上限x在区间上任意变动，则对于每一个取定的x值，定积分有一个确定值与之对应，所以定积分在上定义了一个以x为自变量的函数，我们把称为函数在区间上变上限函数记为图5-10从几何上看，也很显然。

因为X是上一个动点，从而以线段为底的曲边梯形的面积，必然随着底数端点的变化而变化，所以阴影部分的面积是端点x的函数（见图5-10）定积分计算公式利用定义计算定积分的值是十分麻烦的，有时甚至无法计算。

因此，必须寻求计算定积分的简便方法。

我们知道：如果物体以速度作直线运动，那么在时间区间上所经过的路程s为图 5-11另一方面，如果物体经过的路程s是时间t的函数，那么物体从t=a到t=b 所经过的路程应该是（见图5-11）即由导数的物理意义可知：即是一个原函数，因此，为了求出定积分，应先求出被积函数的原函数，再求在区间上的增量即可。

如果抛开上面物理意义，便可得出计算定积分的一般方法：设函数在闭区间上连续，是的一个原函数，即，则这个公式叫做牛顿-莱布尼兹公式。

为了使用方便，将公式写成牛顿-莱布尼兹公式通常也叫做微积分基本公式。

它表示一个函数定积分等于这个函数的原函数在积分上、下限处函数值之差。

它揭示了定积分和不定积分的内在联系，提供了计算定积分有效而简便的方法，从而使定积分得到了广泛的应用。

例1 计算因为是的一个原函数所以例 2 求曲线和直线x=0、x=及y=0所围成图形面积A(5-12)解这个图形的面积为图5-12二、定积分的性质设、在相应区间上连续，利用前面学过的知识，可以得到定积分以下几个简单性质：性质1 被积函数的常数因子可以提到定积分符号前面，即(A为常数)性质2函数的代数和的定积分等于它们的定积分的代数和，即这个性质对有限个函数代数和也成立。