机械原理速度瞬心习题

模拟试题1一、填空题：（30分）1．机构中的速度瞬心是两构件上（相对速度）为零的重合点，它用于平面机构（速度）分析。

2．两构件之间可运动的连接接触称为（运动副）。

3．凸轮的基圆半径越小，则机构尺寸（越大）但过于小的基圆半径会导致压力角（增大）。

4．用齿条型刀具范成法切制渐开线齿轮时，为使标准齿轮不发生根切，应使刀具的（齿顶线不超过极限啮合点）。

5．间歇凸轮机构是将（主动轮的连续转动）转化为（从动转盘的间歇）的运动。

6．刚性转子的平衡中，当转子的质量分布不在一个平面内时，应采用（动平衡）方法平衡。

其平衡条件为（∑M = O ；∑F = 0 ）。

7．机械的等效动力学模型的建立，其等效原则是：等效构件所具有的动能应（等于整个系统的总动能）。

等效力、等效力矩所作的功或瞬时功率应（等于整个系统的所有力，所有力矩所作的功或所产生的功率之和）。

8．平面机构结构分析中，基本杆组的结构公式是（ 3n = 2PL ）。

而动态静力分析中，静定条件是（3n = 2PL ）。

9．含有两个整转副的将铰链四杆机构，以最短杆为( 连杆 )得到双摇杆机构。

10．渐开线齿轮的加工方法分为( 范成法 )和（仿形法）两类。

二、选择题：（20分）1．渐开线齿轮齿条啮合时，若齿条相对齿轮作远离圆心的平移，其啮合角（ B ）。

A) 增大； B)不变； C)减少。

2．为保证一对渐开线齿轮可靠地连续传动，实际啮合线长度（ C ）基圆齿距。

A)等于； B)小于；C)大于。

3．高副低代中的虚拟构件的自由度为（ A ）。

A) -1； B) +1 ； C) 0 ；4．以滑块为主动件的曲柄滑块机构，死点位置出现在（ A ）。

A）曲柄与连杆共线时B）曲柄与连杆垂直时C）曲柄与滑块运动方向平行时D）曲柄与滑块运动方向垂直时5．渐开线齿轮发生根切的根本原因是啮合点跨越了（ A ）。

A）理论啮合线的端点B）实际啮合线的端点C）节点D）齿根圆6．飞轮调速是因为它能（C①）能量，装飞轮后以后，机器的速度波动可以（B②）。

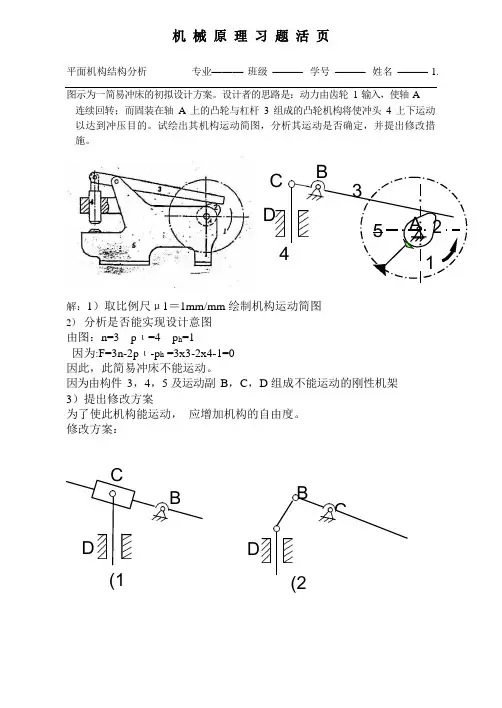
CB D BC平面机构结构分析专业———班级———学号———姓名——— 1.图示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮1 输入，使轴A连续回转；而固装在轴A 上的凸轮与杠杆3 组成的凸轮机构将使冲头4 上下运动以达到冲压目的。

试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。

C B 35 A 24 1解：1）取比例尺μ1＝1mm/mm 绘制机构运动简图2）分析是否能实现设计意图由图：n=3 pι=4 p h=1因为:F=3n-2pι-p h =3x3-2x4-1=0因此，此简易冲床不能运动。

因为由构件3，4，5 及运动副B，C，D 组成不能运动的刚性机架3）提出修改方案为了使此机构能运动，应增加机构的自由度。

修改方案：D(1 (2DG7D 64C EF9 38B 2 A122如图所示为一小型压力机。

图中齿轮 1与偏心轮 1’为同一构件，绕固定轴心 o 连续转动。

在齿轮 5上开有凸轮凹槽，摆杆 4上的滚子 6嵌在凹槽中，从而使摆杆 4 绕 C 轴上下摆动。

同时，又通过偏心轮 1’、连杆 2、滑杆 3使 C 轴上下移动。

最后通过在摆杆 4的叉槽中的滑块 7和铰链 G 使冲头 8实现冲压运动。

试绘制其机构运动简图，并计算自由度。

b)解：计算该机构的自由度n=7， p ι=9， p h =2 F=3n-2p e -p h =3x7-2x8-2=13. 试计算下列二图所示齿轮连杆组合机构的自由度。

图中相切的圆周表示一对齿轮传动的节圆；凡局部自由度、复合铰链和虚约束均需明确指出。

解：a ）解n=4 P ι=5 Ph=1F=3x4-2x5-1=134 C A复合铰链1a)BD 5b）解：n＝6 Pι=7 Ph=3F＝3×6－2×7－3＝14.试计算下列二图所示压榨机的自由度。

图a 中，左右两半完全对称；图b 中，CD = FI = KL = KM = FJ = CE，LI =KF = MJ = JE = FC = ID。

机械原理复习题绪论复习思考题1、试述构件和零件的区别与联系？2、何谓机架、原动件和从动件？第一章机械的结构分析复习思考题1、两构件构成运动副的特征是什么？2、如何区别平面及空间运动副？3、何谓自由度和约束？4、转动副与移动副的运动特点有何区别与联系？5、何谓复合铰链？计算机构自由度时应如何处理？6、机构具有确定运动的条件是什么？7、什么是虚约束？习题1、画出图示平面机构的运动简图，并计算其自由度。

（a）(b) (c)2、一简易冲床的初拟设计方案如图。

设计者的思路是：动力由齿轮1输入，使轴A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。

3、计算图示平面机构的自由度；机构中的原动件用圆弧箭头表示。

(a) (b) (c)(d) (e) (f)第二章 平面机构的运动分析复习思考题1、已知作平面相对运动两构件上两个重合点的相对速度12A A V 及12B B V 的方向，它们的相对瞬心P 12在何处？2、当两构件组成滑动兼滚动的高副时，其速度瞬心在何处？3、如何考虑机构中不组成运动副的两构件的速度瞬心？4、利用速度瞬心，在机构运动分析中可以求哪些运动参数？5、在平面机构运动分析中，哥氏加速度大小及方向如何确定？习题1、试求出下列机构中的所有速度瞬心。

(a) (b)(c) (d)2、图示的凸轮机构中，凸轮的角速度ω1=10s-1，R=50mm，l A0=20mm，试求当φ=0°、45°及90°时，构件2的速度v。

题2图凸轮机构题3图组合机构3、图示机构，由曲柄1、连杆2、摇杆3及机架6组成铰链四杆机构，轮1′与曲柄1固接，其轴心为B，轮4分别与轮1′和轮5相切，轮5活套于轴D上。

各相切轮之间作纯滚动。

试用速度瞬心法确定曲柄1与轮5的角速比ω1/ω5。

4、在图示的颚式破碎机中，已知：x D=260mm，y D=480mm，x G=400mm，y G=200mm，l AB=l CE=100mm，l BC=l BE=500mm，l CD=300mm，l EF=400mm，l GF=685mm，ϕ1=45°,ω1=30rad/s 逆时针。

一、填空题1．机构中的速度瞬心是两构件上（）为零的重合点，它用于平面机构（）分析。

2．下列机构中，若给定各杆长度，以最长杆为连架杆时，第一组为（）机构；第二组为（）机构。

(1) a = 250 b = 200 c = 80 d = 100；(2) a = 90 b = 200 c = 210 d = 100 。

3.机构和零件不同，构件是（），而零件是（）。

4．凸轮的基圆半径越小，则机构尺寸（）但过于小的基圆半径会导致压力角（）。

5．用齿条型刀具范成法切制渐开线齿轮时，为使标准齿轮不发生根切，应使刀具的（）。

6．当要求凸轮机构从动件的运动没有冲击时，应选用（）规律。

7．间歇凸轮机构是将（）转化为（）的运动。

8．刚性转子的平衡中，当转子的质量分布不在一个平面内时，应采用（）方法平衡。

其平衡条件为（）。

9．机械的等效动力学模型的建立，其等效原则是：等效构件所具有的动能应（）。

等效力、等效力矩所作的功或瞬时功率应（）。

10．平面机构结构分析中，基本杆组的结构公式是（）。

而动态静力分析中，静定条件是（）。

一、选择题1．渐开线齿轮齿条啮合时，若齿条相对齿轮作远离圆心的平移，其啮合角（）。

A)增大； B)不变； C)减少。

2．为保证一对渐开线齿轮可靠地连续传动，应便实际啮合线长度（）基圆齿距。

A)等于； B)小于； C)大于。

3．高副低代中的虚拟构件的自由度为（）。

A) -1 ； B) +1 ； C) 0 ；4．压力角是在不考虑摩擦情况下，作用力与作用点的（）方向的夹角。

A)法线； B)速度； C)加速度； D)切线；5．理论廓线相同而实际廓线不同的两个对心直动滚子从动件盘形凸轮，其推杆的运动规律是（）。

A)相同的； B)不相同的； C)不一定的。

6．飞轮调速是因为它能（）能量，装飞轮后以后，机器的速度波动可以（）。

① A)生产； B)消耗； C)储存和放出。

② A)消除； B)减小； C)增大。

7．作平面运动的三个构件有被此相关的三个瞬心。

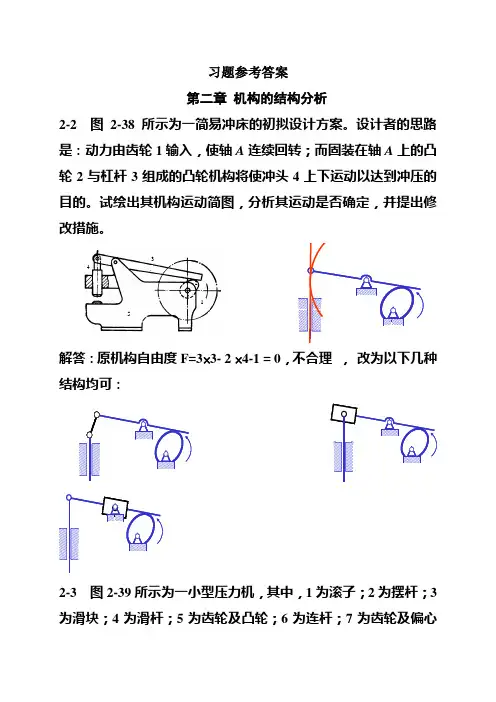
习题参考答案第二章机构的结构分析2-2 图2-38所示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮1输入，使轴A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。

4351 2解答：原机构自由度F=3⨯3- 2 ⨯4-1 = 0，结构均可：1为滚子；2为摆杆；3为滑块；4为滑杆；5为齿轮及凸轮；6为连杆；7为齿轮及偏心轮；8为机架；9为压头。

试绘制其机构运动简图，并计算其自由度。

O齿轮及偏心轮ωA齿轮及凸轮BEFDC压头机架连杆滑杆滑块摆杆滚子解答：n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 = 12-6 试计算图2-42所示凸轮—连杆组合机构的自由度。

解答：a) n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 =1 L 处存在局部自由度，D 处存在虚约束b) n=5; P l =6; P h =2，F=3⨯5-2 ⨯6-2 =1 E 、B 处存在局部自由度，F 、C 处存在虚约束b)a)A EMDFELKJIFBCCDBA2-7 试计算图2-43所示齿轮—连杆组合机构的自由度。

BDCA(a)CDBA(b)解答：a) n=4; P l =5; P h =1，F=3⨯4-2 ⨯5-1=1 A 处存在复合铰链b) n=6; P l =7; P h =3，F=3⨯6-2 ⨯7-3=1 B 、C 、D 处存在复合铰链2-8 试计算图2-44所示刹车机构的自由度。

并就刹车过程说明此机构自由度的变化情况。

解答：① 当未刹车时，F=3⨯6-2 ⨯8=2② 在刹车瞬时，F=3⨯5-2⨯7=1，此时构件EFG 和车轮接触成为一体，位置保持不变，可看作为机架。

③ 完全刹死以后，F=3⨯4-2⨯6=0，此时构件EFG 、HIJ 和车轮接触成为一体，位置保持不变，可看作为机架。

第二章4．在平面机构中，具有两个约束的运动副是移动副或转动副；具有一个约束的运动副是高副。

5．组成机构的要素是构件和转动副；构件是机构中的_运动_单元体。

6．在平面机构中，一个运动副引入的约束数的变化范围是1-2。

7．机构具有确定运动的条件是_（机构的原动件数目等于机构的自由度）。

8．零件与构件的区别在于构件是运动的单元体，而零件是制造的单元体。

9．由M个构件组成的复合铰链应包括m-1个转动副。

10．机构中的运动副是指两构件直接接触所组成的可动联接。

1．三个彼此作平面平行运动的构件共有3个速度瞬心，这几个瞬心必定位于同一直线上。

2．含有六个构件的平面机构，其速度瞬心共有15个，其中有5个是绝对瞬心，有10个是相对瞬心。

3．相对瞬心和绝对瞬心的相同点是两构件相对速度为零的点，即绝对速度相等的点，不同点是绝对瞬心点两构件的绝对速度为零，相对瞬心点两构件的绝对速度不为零。

4．在由N个构件所组成的机构中，有(N-1)(N/2-1)个相对瞬心，有N-1个绝对瞬心。

5．速度影像的相似原理只能应用于同一构件上_的各点，而不能应用于机构的不同构件上的各点。

6．当两构件组成转动副时，其瞬心在转动副中心处；组成移动副时，其瞬心在移动方向的垂直无穷远处处；组成纯滚动的高副时，其瞬心在高副接触点处。

7．一个运动矢量方程只能求解____2____个未知量。

8．平面四杆机构的瞬心总数为_6__。

9．当两构件不直接组成运动副时，瞬心位置用三心定理确定。

10．当两构件的相对运动为移动，牵连运动为转动动时，两构件的重合点之间将有哥氏加速度。

哥氏加速度的大小为a*kc2c3，方向与将vc2c3沿ω2转90度的方向一致。

1．从受力观点分析，移动副的自锁条件是驱动力位于摩擦锥之内，转动副的自锁条件是驱动力位于摩擦圆之内。

2．从效率的观点来看，机械的自锁条件是η＜0。

3．三角形螺纹的摩擦力矩在同样条件下大于矩形螺纹的摩擦力矩，因此它多用于联接。

习题 > 答案一.概念1.当两构件组成转动副时,其相对速度瞬心在转动副的圆心处;组成移动副时,其瞬心在垂直于移动导路的无穷远处;组成滑动兼滚动的高副时,其瞬心在接触点两轮廓线的公法线上.2.相对瞬心与绝对瞬心相同点是都是两构件上相对速度为零,绝对速度相等的点 ,而不同点是相对瞬心的绝对速度不为零,而绝对瞬心的绝对速度为零 .3.速度影像的相似原理只能用于同一构件上的两点,而不能用于机构不同构件上的各点.4.速度瞬心可以定义为互相作平面相对运动的两构件上,相对速度为零,绝对速度相等的点.个彼此作平面平行运动的构件共有 3 个速度瞬心,这几个瞬心必位于同一条直线上 .含有6个构件的平面机构,其速度瞬心共有 15 个,其中 5 个是绝对瞬心,有 9 个相对瞬心.二.计算题1、2.关键:找到瞬心P366 Solution:The coordinates of joint B arey =ABsinφ=°=x =ABsinφ=°= The vector diagram of the right Fig is drawn by representing the RTR BBD dyad. The vector equation, corresponding to this loop, is written asB B+ -=0 or =-Where = and =γ. When the above vectorial equation is projected on the x and y axes, two scalar equations are obtained: rcosφ+π=x -x =rsinφ+π=y -y =Angle φ is obtained by solving the system of the two previous scalar equations:tgφ= φ=°The distance r isr==The coordinates of joint C arex =CDcosφ= y =CDsinφ-AD=For the next dyad RRT CEE, the right Fig, one can writeCecosπ- φ=x - x Cesinπ- φ= y - yVector diagram represent the RRT CEE dyad.r B r r D r r D r B r BD r 3D B 3D B 33141.0541.0⇒3)cos(3πϕ+-B D x x C 3C 34E C 4E CWhen the system of equations is solved, the unknowns φ and x are obtained: φ=° x =7. Solution: The origin of the s ystem is at A, A≡0; that is, x =y =0.The coordinates of the R joints at B arex =l cosφ y = l sinφFor the dyad DBB RTR, the following equations can be written with respect to the sliding line CD:mx - y +n=0 y =mx +nWith x =d , y =0 from the above system, slope m of link CD and intercept n can be calculated: m= n=The coordinates x and y of the center of the R joint C result from the system of two equations:y =mx +n=, x - x +y - y =l Because of the quadratic equation, two solutions are abstained for x and4E 4E A A B 1B 1B B D D D 1D 111cos sin d l l -ϕϕϕϕcos sin 1111l d l d -C C C C ϕϕϕϕcos sin cos sin 1111111l d l d x d l l C -+-C D 2C D 223C Ccontinuous motion of the mechanism, there are constraint relations for the Choice of the correct solution; that is x < x < x and y >0For the last dyad CEE RRT, a position function can be written for joint E:x -x +y -h =l The equation produces values for x and x , and the solution x >x is selected for continuous motion of the mechanism.C BD C CE 2C 2241E 2E E C。

机械原理瞬心法求速度习题引言机械原理是工程力学的一部分，研究物体的运动及力学效应。

在机械原理中，瞬心法是一种常用的分析方法，用于求解物体的速度和加速度。

本文将通过解答一些瞬心法求速度的习题，加深对机械原理的理解。

问题一有一个直径为1m的转盘，上面有一个固定在轴上的活动滑块。

滑块到轴的距离为0.5m。

转盘以5 rad/s的角速度逆时针旋转。

求滑块上某点P的速度。

首先，我们需要确定滑块上的点P的位置。

由于滑块到轴的距离为0.5m，而转盘的直径为1m，因此点P的位置位于滑块上与轴对称的位置，距离轴0.5m。

我们可以使用瞬心法来求解滑块上点P的速度。

瞬心法的基本原理是，在运动过程中，物体的速度等于通过瞬时转动中心与物体上的某一点所作的相对速度。

在本题中，我们可以选择转盘的轴作为瞬时转动中心。

因此，我们需要确定点P相对于转动中心的位置向量和其相对于转动中心的速度向量。

点P相对于转动中心的位置向量为[0.5, 0]，即P的横坐标为0.5m，纵坐标为0，代表距离转动中心0.5m。

点P相对于转动中心的速度向量为[0, R * ω]，其中R 为转盘的半径，即0.5m，ω为转盘的角速度，即5 rad/s。

代入数值计算，得到速度向量为[0, 2.5]，即P点的速度大小为2.5 m/s，方向为垂直于转盘的切线方向。

问题二一个直径为0.8m的小车以2 rad/s的角速度逆时针旋转。

小车上有一根长1.2m的杆，杆上距离小车中心0.6m处有一个质量为1kg的小球。

求小球的速度大小和方向。

我们可以使用瞬心法来求解小球的速度。

同样地，选择小车的中心作为瞬时转动中心。

首先，我们需要确定小球相对于转动中心的位置向量和其相对于转动中心的速度向量。

小球相对于转动中心的位置向量为[0.6, 0]，即小球距离转动中心0.6m。

小球相对于转动中心的速度向量为[0, R * ω]，其中R为小车直径的一半，即0.4m，ω为小车的角速度，即2 rad/s。

第二讲平面机构的运动分析一用速度瞬心法作机构的速度分析1 速度瞬心的定义：作平面相对运动两构件上任一瞬时其速度相等的点，称为这个瞬时的速度中心。

分类：相对瞬心－重合点绝对速度不为零绝对瞬心－重合点绝对速度为零2 瞬心数目 K＝N(N-1)/23 机构瞬心位置的确定直接观察法：适用于求通过运动副直接相联的两构件瞬心位置。

１）两构件组成转动副时，转动副中心即是它们的瞬心。

２）若两构件组成移动副时，其瞬心位于移动方向的垂直无穷远处。

３）若两构件形成纯滚动的高副时，其高副接触点就是它们的瞬心。

４）若两构件组成滚动兼滑动的高副时，其瞬心应位于过接触点的公法线上。

不直接形成运动副的两构件利用三心定理来确定其具体位置。

三心定理：三个彼此作平面平行运动的构件共有三个瞬心，且它们位于同一条直线上。

此法特别适用于两构件不直接相联的场合。

4传动比的计算ωi /ωj＝P1j P ij / P1i P ij两构件的角速度之比等于绝对瞬心至相对瞬心的距离之反比5.角速度方向的确定相对瞬心位于两绝对瞬心的同一侧，两构件转向相同相对瞬心位于两绝对瞬心之间，两构件转向相反。

常见题型：1.速度瞬心的求解、2利用速度瞬心求解速度。

二、用矢量方程图解法作机构的速度和加速度分析 1．同一构件上两点之间速度，加速度的关系。

①由各速度矢量构成的图形称为速度多边形（或速度图）；由各加速度矢量构成的图形称为加速度多边形（或加速度图）。

p ，'p 称为极点。

②在速度多边形中，由极点p 向外放射的矢量，代表构件上相应点的绝对速度。

而连接两绝对速度矢端的矢量，则代表构件上相应两点间的相对速度，方向与角标相反，如代表CB v （C 点相对B 点的速度）。

③在加速度多边形中，由极点'p 向外放射的矢量代表构件上相应点的绝对加速度。

而连接两绝对加速度矢量端的矢量代表构件上相应两点间的相对加速度，方向与角标相反。

相对加速度可用其法向加速度和切向加速度来表示。