当前位置：文档之家 › 信息光学chap4透镜的位相调制和傅里叶变换性质

信息光学chap4透镜的位相调制和傅里叶变换性质

  • 格式：ppt
  • 大小：705.50 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

第4章 透镜的位相调制和傅里叶变换性质

第4章 透镜的位相调制和傅里叶变换性质

发散球面波和会聚球面波在透镜平面上都具有球 面波的二次位相因子，因此透镜的功能就是改变 二次位相因子的大小，实际上也就是具有附加的 二次位相因子。
透镜的位相变换作用
基本假设 • 透镜是薄的, 忽略折射引起的光线的横向偏移 • 透镜无吸收, 完全透明, 均匀,折射率为n，不改 变光场振幅,仅改变位相 • 透镜孔径为无限大 (以后再考虑孔径影响)
1、透镜的位相调制作用 1.1 透镜对入射波前的作用——分析复振幅透过率
这是在傍
轴近似下的完 善成像，发散 球面波经过透 镜变换成会聚 球面波。
透镜的复振幅透过率：
tl
(
x,
y
)

U U
l( l(
x, x,
y) y)
Ul (x,y) 和Ul (x,y) 分别
是紧靠透镜前后平面上
的光场复振幅分布。
P

x,
y

1
0
透镜孔径内 其他
1、透镜的位相调制作用
于是透镜的复振幅透过率可以完整的表示为：
tl

x,
y


exp

j
k 2f
x2 y2

P

x,
y


其中，
exp

j
k 2f
x2 y2


表示透镜对入射波前的位相调制；
P ( x, y ) 表示透镜对于入射波前大小范围的限制。
tl (x, y) exp j(x, y)
1、透镜的位相调制作用
tl x, y exp j x, y exp jkL x, y
L(x,y)是Q到Q之间的光程：
4透镜的Fourier变换性质

4透镜的Fourier变换性质

k
2 2
z u 2 ( x2 , y 2 ) e i d 0 d i
i
k1 z (1 )( x 2 y 2 ) z di di
U ( x , y )e
t 1 1

i
k z (1 ) 2 d0 d0
e
i 2 [
z ( xx yy )] d0 d1 1 1
dxdy
S
d
S
0
U ( x, y )
i
di
透镜的透过率函数为
2 2 k 1 1 U t ( x, y ) i ( )( x y ) t l ( x, y ) e 2 di d0 U i ( x, y )
1 1 由f (n 1)( )薄透镜物像关系公式 R1 R2 和tl ( x, y )＝e
2
x . f y . f
fx
fy
结论 : 平面波照射下, 正入射, 在透镜焦面上得 到t ( x1 , y1 )的d0 , 不论d0为何值, 导致一个二次位 相因子.但位相弯曲不影响光强.观察焦面上的 强度分布没有影响,仍为功率谱.
三、单色球面波照射孔径平面
a0 k 2 2 球面光场U i ( x1 , y1 ) exp{i ( x1 y1 )} 2 透射场U t ( x1 , y1 ) U i ( x1 , y1 )t ( x1 , y1 )代入 * 式 z k z 2 2 焦面光场U 2 ( x2 , y2 ) exp{i (1 )( x2 y2 )} t ( x1 , y1 ) i d i d 0 2d i d0 k z d0 z exp[i (1 )]exp[i 2 ( x1 x2 y1 y2 )]dx1dy1} 2 d d0 di
信息光学课件 透镜的傅里叶变换性质

信息光学课件 透镜的傅里叶变换性质

P1 p2 p3
p4
P2 面的光场为 f (x, y) 对入射光的菲涅耳衍射：
UP2
U P1
h，h
1 i z
（略去相位因子 e e ikz
ik ( x2 y2 ) 2z
ikz
ei
）
UP2
1 d1
f (x, y) ei (x2 y2 ) ，
k 2d1
P3 面场分布：（U P2 乘以 P2 (x, y) ）
1 i f
ei f
f
(
f
2 x
f
2 y
)
F
(
f
x
,
fy)
透镜后焦面物的傅立叶谱含有一位相位因子 ei f
f
(
f
2 x
f
2 y
)
，（空间频谱
按一定比例缩放）。
2，物置于透镜前的傅立叶变换关系。
首先作向化处理：
a，忽略透镜孔径影响， P(x, y) =1。
b，单位振幅平面波垂直照明，在透镜后焦面观察衍射场。
d2 f ；
则，
g(x, y)
1
i (1 d1 )( x2 y2 )
e f f
i2 ( x y )
f ( ,)e f f d d
存在位相弯曲。

（下面讨论特殊情况）
a，物置于透镜前焦面时。
d1
f
， g(x, y) 1
i f
F( fx,
f y ) ，（
fx
x f
，
fy
y f
）
位相弯曲消失：得到准确的傅立叶变换。☆
b，物紧贴透镜前表面。
d1 0
g(x, y)
1 i f
第四章 透镜的位相调制 和傅里叶变换

第四章 透镜的位相调制 和傅里叶变换


傍轴近似下单色点光源的发散球面波在平面上造成的光场分布为
U 1 ( x, y ) = A exp( jkp ) exp[ j k ( x 2 + y 2 )] 2p
球面波经透镜变换后向点会聚，在平面上造成的复振幅分布为
k U 1' ( x,y )= Aexp( jkq )exp j (x 2 + y 2 ) 2q
照明光源和观察平面的位置始终保持共轭关系，因此观察平面位 照明光源和观察平面的位置始终保持共轭关系 置由照明光源位置决定（当照明光源位于光轴上无穷远，即平面 波垂直照明时，这时观察平面位于透镜后焦面上） 输入平面位于透镜前焦面，由于 d 0 = f ，衍射物体的复振幅透 输入平面位于透镜前焦面 过率与衍射场的复振幅分布存在准确的傅里叶变换关系，而且只 要照明光源和观察平面满足共轭关系，与照明光源的具体位置无 关。也就是说，不管照明光源位于何处，均不影响观察面上空间 频率与位置坐标的关系
= mm
50 = 463mm 3 0.6 10 180
( f d0 )(x2 + y2 ) ∞ f (x0 x + y0 y) ′ exp jk U(x, y) = c ]dx0dy0 ∫∫ t(x0 , y0 ) exp[ jk q( f d0 ) + fd0 2[q( f d0 ) + fd0 ]∞
两个特殊位置的讨论 两个特殊位置的讨论
( f d 0 )(x 2 + y 2 ) ∞ d0 d0 U ( x,y )=c ′exp jk ∫ ∫t (x0 ,y 0 )P x 0 + x,y 0 + 2f 2 f f ∞ x0 x+ y 0 y exp jk dx0 dy 0 f y ×
第四章 透镜的位相调制和FT变换性质

第四章 透镜的位相调制和FT变换性质


理解透镜位相因子的物理意义 可通过考察透镜对垂直入射的单位振幅平面波的 效应，来理解透镜位相因子的物理意义
U 设： l x, y 为紧贴透镜前面的平面波光场分布， U lx, y 为紧贴透镜后面的平面上的光场复 振幅分布，
二者之间有关系如下：
U lx, y U l x, y tl x, y , 或 tl x, y U lx, y U l x, y
2 1 2 2


x2 y2 D 2 x, y D 02 R2 R x y D 02 R2 1 1 2 R2
2 2 2 2


x2 y2 x2 y2 Dx, y D 0 R1 1 1 2 R2 1 1 2 R1 R2 其中： D 0 D 01 D 02
在傍轴近似条件下： 考虑在透镜轴附近的那部分波前，即(x2+y2) 值足够小，则下列近似式成立。
x2 y2 x2 y2 1 1 2 R1 2 R12 x2 y2 x2 y2 1 1 2 R2 2 R22
上式相当于用抛物面来近似透镜傍轴区域的球面。 厚度函 数变成
x2 y2 x2 y2 R2 1 1 Dx, y D 0 R1 1 1 2 2 2 R1 2 R2 x2 y2 1 1 D0 2 R1 R2
A I f x f , y f f yy f dxdy
T0 u , v
2

2
二、 物体位于透镜之前
At0 x0 , y0 U l x, y U l x, y
1 P x, y 0 透镜孔径内 其他
光学透镜的变换总结

光学透镜的变换总结


U 1 (x, y) ? A exp( jkp) exp[
j k (x 2 ? y 2 )] 2p
球面波经透镜变换后向点会聚，在平面上造成的复振幅分布为
U' ?
?x,y ??
Aexp??
jkq ?exp ???
?
j
k ?q
?x
?
?
y
?
???
?
透镜的复振幅透过率或相位变换因子为
t (x, y) ? U1?(x, y) ? exp[ U1(x, y)
输入平面位于透镜前焦面，由于 d0 ? f，衍射物体的复振幅透过率与衍
射场的复振幅分布存在准确的傅里叶变换关系，而且只要照明光源和观察 平面满足共轭关系，与照明光源的具体位置无关。也就是说，不管照明光 源位于何处，均不影响观察面上空间频率与位置坐标的关系
???
U (x, y) ? c?
??
t( x0 , y0 ) exp(?
物在透镜之后的变换性质证明（ 2）
这个光场传输到观察平面上造成的场分布为
exp[ ? ? U (x, y) ?
1
j? (q ? d 0 )
t( x0 , y0 )U 0 ( x0 , y0 ) ?0
jk
(x
?
x0)2 ? 2(q ?
(y ? d0 )
y0 )2
]dx0 dy0
经过一系列的代数演算得到：
光学透镜的变换
透镜的位相变换作用
透镜是光学系统的最基本的元件，具有成象和光学傅里叶变换的 基本功能，本章将首先讨论透镜的成像和光学傅里叶变换性质
透镜可以用来实现透过物体的光场分布的夫琅和费衍射，而透镜 之所以可以实现傅里叶变换的原因是它具有位相变换的作用
第四章 透镜位相调制和傅里叶变换性质

第四章 透镜位相调制和傅里叶变换性质


xi x0 yi y0 1 1 1 2 2 ( )( x y ) 2( ) x 2( ) y dxdy dx0dy0 di d1 f di d1 di d1
可以证明，当观察平面是照明光源S的共轭平面时，即
1 1 1 di d0 f
x y k U ( xi , yi ) C exp j ( xi2 yi2 ) t ( x0 , y0 ) exp j 2 ( i x0 i y0 ) dx0dy0 2 xi yi k 2 2 ℱ t ( x , y ) fx C exp j ( xi yi ) fy 0 0 2
xi fx f yi fy f
当透镜孔径大于物体限度时，物体上的信息全部通 过透镜，孔径没有影响；当透镜孔径小于物体限度时， 必须考虑孔径的影响，卷积的作用使得频谱面上的频谱 与物体的频谱之间产生失真，孔径越小，失真越严重。
t(x0,y0)
2.物体放在透镜后方 会聚光在物体上投影的等效孔径函数为
第四章 透镜的位相调制和傅里叶变换性质
透镜是最基本、最重要的光学元件。众所周知，它可 以对物体进行成像，其实质是改变光波的波前。同时它还 能对物体进行傅里叶变换。
§4—1 透镜的位相调制作用
透镜一般由两个球面构成，当光线入射到不同的 位置时，由于各点厚度不同，其位相延迟是不同的。
如图所示，单位振幅平行光垂直入射在透镜的前表面，光场为
1 1 1 由于 d0 di f
x2 y2 t ( x, y ) U 0 exp( jk ) 2f
一般情况下，透镜的位相调制作用为
x2 y 2 tl ( x, y ) exp( jk ) 2f
信息光学专题知识讲座

信息光学专题知识讲座

(1)傅立叶变换。
(2)成像。
透镜一般由光密介质玻璃(n=1.5)做成。
1. 薄透镜旳位相调制作用 薄透镜：就是厚度和透镜表面曲率半径相比很小旳透镜。
对于薄透镜，能够近似
以为光线进入透镜旳位
O
I
置（x,y）与光线射出透
镜旳位置相同。
所以，一种薄透镜旳作用只是使入射波前受到延迟，延迟旳 多少正比于透镜各点旳厚度。
fy)
其中
fx
x0
f
,
fy
y0
f
与2-4-13式比较后不难发觉，这正是f(x,y)旳夫琅和费衍射 成果！正是因为这个原因，实践中夫琅和费衍射试验往往 都是经过一种正透镜来实现旳。
g( x0, y0 ) 还不是 f ( x, y) 旳傅立叶变换，它多了一种相位因子；
exp if ( fx2 f y2 )
3－1 透镜旳傅立叶变换性质
对于透镜，我们并不陌生，透镜是光学成像系统最主要旳 器件，我们这里讲透镜不是从几何光学旳角度去讨论它，而是 从波动光学旳角度去研究它，同学们会随即旳讨论中发觉讨论 旳成果和几何光学旳成果完全一致。当然，衍射旳效果是不能 用几何光学旳措施去讨论旳。 透镜有两个非常主要旳性质：
磨镜者公式：
1 f
(n
1)
1 R1
1 R2
假如用单位振幅旳平面波入射到透镜上，这时入射波复振幅，
U1(x, y) 1
出射光波复振幅，
U2(x, y)
U1( x, y)PL ( x, y)
exp i
k 2f
(x2
y2 )
2. 透镜旳傅立叶变换性质
会聚透镜最突出旳旳性质之一就是它固有旳进行二维傅立叶变换 旳本事。 假定光源是单色旳，也就是说我们所研究旳系统是相干系统。
第十四章傅里叶光学-文档资料

第十四章傅里叶光学-文档资料

22 H u , v exp j d u v 0

u
x y 1 v 1 d0 d0
~ x E 2, y 2
Ex ,y 1 1
~ Ex, y

t x ,y l 2 2
t x ,y 1 1
~ 而 FT E x ,y 1 1 A FT tx ,y A T u , v 1 1


2 f


~ ~ x E ,y 1 1 E x ,y 1 1
~ Ex, y


f
f
表明：透镜后焦面上的光场分布正比于 tl x ,y 衍射物体平面上复振幅的傅里叶变换。 tx 1 1 f ,y 1 1
jk 2 2 exp 2f x y ，后焦面上的位相分布与物体频谱的位相分布不
tx, y
tl x, y f
~ 2）紧靠透镜之后的平面上的复振幅分布E x ,y 1 1
~ 3）后焦面上的复振幅分布 Ex, y
,y 物体的复振幅透过率为tx ，则物体与透镜之间的平面上的 1 1 复振幅分布为 ~ E x , y A t x , y 1 1 1 1





k 2 2 代入上式得到 ~ 将 E x , y A t x , y exp j x y 1 1 1 1 1 1
jk 2 1 2 Ex, y exp x y j f 2f ~ x y FTEx 1, y 1 u 1 v 1
但是这种FT关系不是准确的。由于变换式前存在位相因子


一样，但他对观察平面上的强度分布没有影响，其光强为
A x y I x , y T , f f f f
信息光学(傅里叶光学)Chap4-1

信息光学(傅里叶光学)Chap4-1

x
z
y
z
在无穷远处观察到衍射屏的二维傅里叶变换. 能否在有限远处观察和利用? 可以用透镜实现. 几何光学中,透镜是折射成像 元件, 将物点变换为像点, 物、 像点均可在无穷远 物理光学中,透镜是实现位相 变换的元件, 其前后表面的光 场复振幅分布不同. 本章解决: 透镜的位相变换, 透镜的F.T.性质
只要正确决定R1、R2的符号, 以上推导适合于任何透镜
透镜的焦距
1 1 f (n 1) R R 2 1
1
仅决定于透镜材料和几何参数.
此结果与几何光学一致. f >0: 凸(正)透镜; f <0: 凹(负)透镜
x2 y2 不考虑常数位相因子, 则透镜的位相变换因子为 exp jk 2f 此变换与入射波的复振幅无关, 它实现变换:
m为整数
令ar02 = u, 则复振幅透过率是u的周期函数, 周期为2p. 方波, 可以展开为复指数 1 1 sgn(cosu ) cn exp( jnu ) 形式的傅里叶级数: n (1)求出傅氏系数cn, 2 2 (2)讨论n为奇数和偶数的情形 (3)与上例的结果相比较.
§4-1 透镜的位相调制作用: 例 讨论
此屏类似透镜, 等效于平、凹、凸三个透镜,可作位相变换 三个透镜的直径为2l, 焦距分别为∞, -p/a和 p/a. 当单色平面 波垂直入射时, 有三部分出射光束 (1)直接透过,循原方向传播 (2)会聚到透镜后焦面处, 与透镜距离为p/a (3)从透镜前焦点p/a处发散的球面波 正、负透镜的焦距与波长有关, 即有很大的色差. 只有用单色光照明,才能得到清晰的像 三个衍射级不能完全分开
与(x,y)平面上球面波复振幅分布的位相因子相比较 f >0: Ul’(x,y)代表会聚到透镜后焦点的会聚球面波; f <0: Ul’(x,y)代表从透镜前焦点发出的发散球面波 这与几何光学的结果相同 若考虑透镜的有限尺寸, 可引入孔径函 P ( x, y ) 1 数P(x,y), (一般是圆域函数或矩孔函数), 0
第十四章傅里叶光学

第十四章傅里叶光学

1 1
E ( x1 , y1 )
2、点物在距透镜有限远的光轴上 、 设点物S位于距透镜为 l 的光轴上， 设点物 位于距透镜为 的光轴上， 则投射到透镜上的光波就是从S点 则投射到透镜上的光波就是从 点 发出的发散球面波。在傍轴近似下， 发出的发散球面波。在傍轴近似下， 它在透镜前平面上的场分布为
x12 + y12 ~ E ( x1 , y1 ) = A exp ik 2l
由于不考虑透镜的有限孔径大小， 由于不考虑透镜的有限孔径大小，则透镜的复振幅透过率为
2 2 x1 + y1 tl (x1 , y1 ) = exp − ik 2f
则紧靠透镜之后的平面上的复振幅分布为
E ′(x1 , y1 ) = tl ( x1 , y1 ) ⋅ E ( x1 , y1 ) k 2 2 = A ⋅ t (x1 , y1 ) exp− j x1 + y1 2f
(
)
{
}
所以
~ (x , y ) = A exp jk E jλ f 2 f
x y d0 2 2 1 − x + y ⋅ T , λf λf f
(
)
可见后焦面上的复振幅分布仍然正比于物体的傅里叶变换， 可见后焦面上的复振幅分布仍然正比于物体的傅里叶变换，到 有一个位相弯曲。 物体紧靠透镜结论与前面一致， 有一个位相弯曲。当 d 0 = 0 时，物体紧靠透镜结论与前面一致， 当 时 d 0 = f，式子变为 x y
tl ( x1 , y1 ) f
但是这种FT关系不是准确的。 但是这种 关系不是准确的。由于变换式前存在位相因子 关系不是准确的
jk 2 exp x + y2 2 f

信息光学原理第3章


1
焦面场是透镜前端场的傅里叶变换(空间频谱)。 如上图所示，距离透镜前端有一物体，其透过率为t(x0,y0)。若用振幅为A 的平面波垂直照明物体，则物体的透射光场为：
U0 x0 , y0 A t x0 , y0
根据角谱理论，透镜前端场的角谱为：
F U1 x, y F U 0 x0 , y0 H f x , f y
U l x, y U x, y
在傍轴近似下，忽略透镜对光波振幅的影响，紧靠透镜前后的平面上产生的 复振幅分布为
k U l x, y A exp jkd 0 exp j x 2 y 2 2d 0
k U l x, y A exp jkd i exp j x 2 y 2 2d i
x 1
2
y2 R12
x 1
x2 y 2 1 2 R2 2 2 x y 2 x, y 02 R2 R2 2 x 2 y 2 02 R2 1 1 2 仅考虑傍轴光 R2
f

f
f

j f



2f

2
2
f
f


k 2 U 2 x, y exp j x 2 y 2 exp j xx f yy f dxdy 2f f
?
3.2 透镜的傅里叶变换性质
后焦面上的场分布为
3.1 透镜的位相调制作用
则透镜复振幅透过率表示为：
k A exp jkdi exp j x 2 y 2 U x, y 2d i tl x, y l U l x, y k 2 2 A exp jkd 0 exp j x y 2d 0

4_透镜的傅里叶变换性质

透镜的傅里叶变换
• 1、透镜对入射波前的变换作用
• 2、透镜的富里叶变换分析方法
– 传统分析方法(三种情况分析) – 普遍性推导（二次菲涅尔衍射推导，有一定新意） – 物体放置在透镜距离一定距离后的详解(更加科学） – 透镜为什么具有傅里叶变换性质？
• 3、透镜的傅里叶变换性质
– 透镜为什么具有傅里叶变换特性 – 4F系统为什么可以成镜像
• 4、透镜的孔径对傅里变换的影响
• 5、共轭照明下透镜的傅里叶变换特性（新）
• 6、透镜傅里叶变换的应用
2015/4/2
第四章 透镜的傅里叶变换性质
1
一、透镜的光波变换性质
– 1.0 棱镜与透镜
2015/4/2
第四章 透镜的傅里叶变换性质
2
一、透镜的光波变换性质
– 1.1、透镜的几何光学表述
透镜成像图解
L(x,y)表示光线在入射和出射平面的光程
L(x,y)=n△(x,y)+[△0-△(x,y)]=△0+(n-1)△(x,y)
tl(x,y) exp( jkΔ0 ) exp jk(n-1)Δ(x,y)
2015/4/2
第四章 透镜的傅里叶变换性质
7
一、透镜的光波变换性质
– 1.3、透镜的厚度函数
tl (x, y) exp( jkn0 ) exp

j
k 2f
(x2

y2 )
注意：大多数情况下， kn0 绝对位相并不重要，可以忽略
2015/4/2
第四章 透镜的傅里叶变换性质
9
透镜的光波变换性质
– 1.3、透镜的相移函数：特例
当入射光波为平面波时
Ul(x, y)

信息光学_第四章


x0 y0
x y
xf yf
U2
Uf

Fresnel U ( x, y) exp jkz exp[j k ( x 2 y 2 )] U x , y exp[j k ( x 2 y 2 )]exp[ j 2 ( xx yy )]dx dy 0 0 0 0 0 0 0 0 jz 2z 2z z 公式：
exp[ jk ( p q)]
常数相位因子，改变光波整体的位相分布，可略掉
k 1 1 调制项，影响观察面上位相的相对分布， exp[ j ( x 2 y 2 )( )] 把发散球面波变换成会聚球面波 2 p q
透镜成像的高斯公式：
1 1 1 p q f
所以，透镜的位相变换因子为：
k ( x 2 y 2 )] 2f
将公式
U 2 ( x, y ) U1 ( x, y ) exp[ j
代入上式
x0 y0
x y
xf yf
U2
Uf

exp jkf k 2 2 2 U f (x f , y f ) exp[j ( x f y f )] U1 x, y exp[ j ( xx f yy f )]dxdy jf 2f f
xf yf
Uf
U 2 ( x, y)
透镜位相变换因子
• 透镜后端面光场复振幅
k U 2 ( x, y ) U1 ( x, y ) exp[ j ( x 2 y 2 )] 2f
• 透镜焦平面上光场复振幅 U f ( x f , y f )
透镜后端面光场
透镜后焦面光场， 属于Fresnel衍射。
令：
exp jkf k 2 2 U f (x f , y f ) exp[ j ( x f y f )] j f 2f U 2 x, y exp[ j

4透镜相位调制与傅里叶变换性质


U l x, y 1
透镜将平面波变成球面波
略去透镜的常量位相延迟，紧靠透镜后 的平面上的复振幅分布为
k ' 2 2 U l ( x, y ) U l ( x, y ) tl ( x, y ) exp j x y 2f'


旁轴近似下，这是一个球面波的表达式。
(孔径+透镜)(有限大小,有衍射作用,位相变换作用) + 光在自由空间的传播(菲涅耳衍射) 逐面计算,在不同的几何配置下可以得到傅里叶变换或成像
信息光学
INFORMATION OPTICS
4.1 透镜的位相调制作用
几何光学中,透镜是折射成像元件, 将物点变换为像点, 物、 像点均可在无穷远。 物理光学中,透镜是实现位相变换的元件, 其前后表面的光场 复振幅分布不同。


物体紧靠透镜的傅里叶变换光路
' l
于是有：
k 2 2 U ( x, y ) U l ( x, y ) tl ( x, y ) At ( x, y ) exp j x y 2f'


光波从透镜传播 f’ 距离后，到达后焦面上所产生的场分布可根 据菲涅耳公式计算。
S1
x-y
2. S1、S2面是同一x-y 平面的前后表面
S2
信息光学
INFORMATION OPTICS
4.1.1 透镜对于入射波前的作用
S1面是发散球面波分布： S2面是会聚球面波分布: 略去常数位相因子 透镜的复振幅透过率 或相位变换因子为：
k 2 2 U l ( x , y ) A exp( jkd 0 ) exp j ( x y ) 2d 0

第四章 透镜的位相调制和傅里叶变换性质


tl x, y exp jk0 exp jk n 1 x, y
x, y 0
x2 y2 2
1 1
R1
R2
tl x, y exp jkn0 exp jk n 1
x2 y2 2
1 R1
1 R2
1 f
n
1
1 R1
1 R2
tl
x,
y
exp
jkn0
exp
x,
y
传播：光波由一个平面向另一个平面传播一段距离，用菲
涅尔衍射处理
U0 x0 , y0 Ul x, y Ul x, y U f x f , y f
Ul x, y
1 k
j d1
exp
j
2d1
x2 y2
F U0
x0 ,
y0
exp
j
k 2d1
x02 y02
xf
d
,
fy
yf
d
透镜后焦面上的复振幅分布正比于物体的傅里叶变换
对应的强度分布为
I f
xf , yf
Af
d 2
2
T
xf
d
,
yf
d
2
知识点回顾
透镜的复振幅透过率
tl (x, y) exp[ j
k 2f
(x2
y2 )]
1 f
n
1
1 R1
1 R2
考虑透镜孔径
tl (x, y)
exp[
(x,
y)
exp
j
2
f
x2 y2
U f
xf , yf
exp
j
jkf f
exp
j

《信息光学》第四章章透镜的位相调制和傅里叶变换性质


tl x, y exp jk 0 exp jk n 1 x, y
x, y 0
x
2
y2 1 1 2 R1 R2
x2 y 2 1 1 tl x, y exp jkn0 exp jk n 1 2 R1 R2
1 1 1 n 1 f R1 R2
(n为透镜材料的折射率)
k tl x, y exp jkn0 exp j x 2 y 2 2f
常数项
透镜位相因子
1、透镜的位相调制作用
以上推导的关系适用于各种形式的薄透镜，而且是在旁轴近似条件下推
1
焦面场是透镜前端场的傅里叶变换(空间频谱)。 如上图所示，距离透镜前端有一物体，其透过率为t(x0,y0)。若用振幅为A 的平面波垂直照明物体，则物体的透射光场为：
U0 x0 , y0 A t x0 , y0
根据角谱理论，透镜前端场的角谱为：
F U1 x, y F U 0 x0 , y0 H f x , f y
x 1
2
y2 R12
x 1
x2 y 2 1 2 R2 2 2 x y 2 x, y 02 R2 R2 2 x 2 y 2 02 R2 1 1 2 仅考虑旁轴光 R2
则
tl x, y exp jk 0 exp jk n 1 x, y
上式具有普遍意义，对于任意面形的薄位相物体，一旦知道其厚度函数(x,y)， 就可以根据该式得到其位相调制。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

U0 (x0,y0,0-) x0 U0 (x0,y0,0+)
实现位相变换:
y0 t(x0,y0)
U0 (x0,y0,0+)= U0 (x0,y0,0-) t(x0,y0)
Ul '(x',
y')
Ul (x',
y') exp
jk
x'2 y'2 2f
透镜光瞳函数：P(
x',
y')
1 0
透镜孔径内 其它
2
)
P2面是会聚球面波分布:
Ul
' ( x,
y)
Aexp(
jkq) exp
j
k 2q
(x2
y
2
)
略去常数位相因子 透镜的复振幅透过率 或相位变换因子为：
t(x,
y)
Ul(x, Ul (x,
y) y)
exp
j
k 2
(x2
y2 )
11 1 qp f
f 为透镜的像方焦距。
y2
)]
1 4
exp[
ja(x2
y
2
)]circ
x2 y2 l
设a>0, 分别考察圆括号中的三项:
exp[
ja(x2
y2)]
exp
jk
x2
y2
2
k 2a
exp[ ja(x2 y2 )] exp jk
x2 y2
2
k 2a
代表正透镜
焦距f = k/2a = p/al
解:
t(x,
y)
t(r)
1 2
1 2
cos(ar
2
)
circ
r l
1
2
1 2
e jar2
e 2
jar 2
circ
r l
1
2
1 4
exp[
ja( x 2
y2
)]
1 4
exp[
ja( x 2
y2
)]
circ
x2 y2
l
t(x,
y)
1
2
1 4
exp[
ja(x2
只要傍轴条件满足，薄透镜就会以上述形式对Ul(x,y)进行相 位变换。
任何衍射屏,若其复振幅透过率可写为 看成一个焦距为 f 的透镜！
exp jk
x2 y2
2f
的形式,都可
例题（作业4.8）
屏的复振幅透过率:
t ( x,
y)
t(r)
1 2
1 2
cos(ar 2
)circ
r l
问: 1. 是否类似透镜? 2. 焦 距? 3. 成像的波长特性?
波垂直入射时, 有三部分出射光束
(1)直接透过,循原方向传播
(2)会聚到透镜后焦面处, 与透镜距离为p/al (3)从透镜前焦点p/al 处发散的球面波
正、负透镜的焦距与波长有关, 即有很大的色差。 只有用单色光照明,才能得到清晰的像。
用全息方法很容易实现上述透过率函数, 此屏即为同轴全息透 镜, 是球面波与平面波干涉的结果
第四章 透镜的 位相调制和傅里叶变换性质
从单透镜的位相变换作用入手,导出透镜 的傅里叶变换性质和成像性质；
将透镜成像看成线性不变系统的变换， 研究评价透镜成像质量的频域方法。
分析方法 (孔径+透镜)(有限大小,有衍射作用,位相变换 作用) + 光在自由空间的传播(菲涅耳衍射)逐 面计算,在不同的几何配置下可以得到傅里叶 变换或成像
传播
光波由一个平面(x0,y0)向另一个平面(x,y)传播一段距离(z)
x0
U0 (x0,y0)
y0
x
U (x,y)
z
z
y
有限距离的传播用菲涅耳衍射处理.在空域有二种表达形式：
菲涅耳衍射公式
观察平面
空域 U(x, y)
孔径平面
U(x0, y0)
U (x, y)
无像差的正薄透镜对点光源的成像过程：
薄透镜近似：
1.忽略折射引起的光线
S’ z 的横向偏移
SS
O1 O2
2. P1、P2面是同一xy平 面的前后表面
p
x-y
q
P1 P2
从几何光学的观点看，图示 的成像过程是点物成点像
从波面变换的观点看 透镜将一个发散球面波变换成一个会聚球面波。
发散球面波在给定平面上的的复振幅分布为：
U (x,
y)
a0 z
exp(
jkz) exp
j
k 2z
[( x
x0 )2
(y
y0 )2 ]
定义透镜的复
振幅透过率:
S’ z
SS
O1 O2
t(x, y) Ul '(x, y)
Ul (x, y)
p
x-y
q
P1 P2
P1面是发散球面波分布：Ul
(x,
y)
Aexp(
jkp)
exp
j
k 2p
(x2
y
代表负透镜
焦距f = -k/2a = -p/al
1 2
1 2
exp
jk
x2
y2
代表平镜, 焦距f =∞, 无焦度, 仅衰减振幅 circ(r0/l)是孔径函数P(x,y), 代表直径为l的圆孔.
此屏类似透镜, 等效于平、凹、凸三个透镜,可作位相变换
三个透镜的直径为2l, 焦距分别为∞, -p/al和 p/al。当单色平面
4.1 透镜的位相调制作用
几何光学中，透镜是折射成像元件， 将物点变换为像点， 物、像点均可在无穷远。
物理光学中，透镜是实现位相变换的元件， 其前后表面 的光场复振幅分布不同。 需要首先解决: 透镜的位相变换，透镜的F.T.性质
基本假设 ●透镜是薄的, 忽略折射引起的光线的横向偏移 ●透镜无吸收, 完全透明, 均匀,折射率为n,不改变光场振幅,仅改 变位相 ●透镜孔径为无限大 (以后再考虑孔径影响)
U
' l
(
x,
y)
exp
jk
x2 y2 2f
这是一个球面波的表达式
与几何光学的结果相同
实际透镜有一孔径，透镜孔径函数（光瞳函数）为
1， 透镜孔径内 P(x, y) 0， 其它 透镜的相位变换因子为 t(x, y) P(x, y) exp[ j k (x2 y2 )]
2f 透镜对光波的相位变换作用，是由透镜本身的性质决定的， 与入射光波复振幅Ul(x,y)的具体形式无关。 Ul(x,y)可以是平面波的复振幅，也可以是球面波的复振幅， 还可以是某种特定分布的复振幅.
透镜的相位变换因子可简单地表为 t(x, y) exp[ j k (x2 y 2 )]
2f
此变换与入射波的复振 幅无关, 它实现变换:
Ul '(x, y) Ul (x, y) exp
jk
x2 y2
2f
单位振幅的平面波垂直入射，P1面上的复振幅分布Ul(x,y)=1， 在平面P2上造成的复振幅分布为:
#
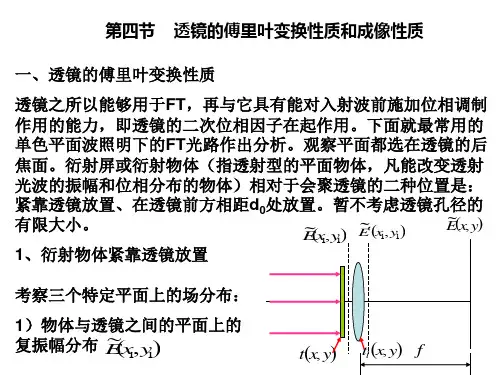
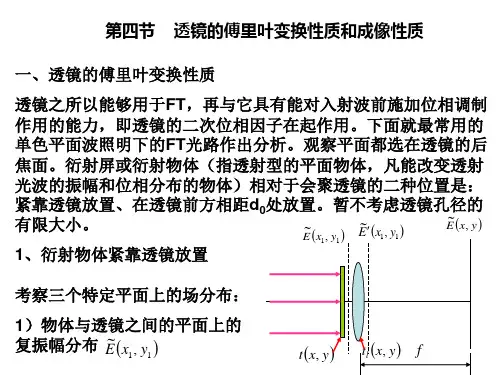
4.2 透镜的傅里叶变换特性
目的 证明: 平面型透明片，在单色光照明下，通过透镜的
位相调制作用，在照明光源的共轭平面上可以得到透明片的 傅里叶变换。
光学系统的一般描述
光学系统由孔径和透镜组成,光波由一个平面向另一个平面传播
孔径:真实开孔,屏,透明片等 用复振幅透过率t(x0,y0)描述
透镜: Ul (x’,y’) Ul’ (x’,y’)