积的乘方
- 格式:doc
- 大小:72.00 KB
- 文档页数:6

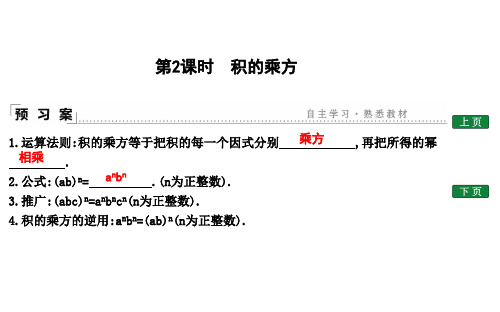




积的乘方法则和公式
《积的乘方法则和公式积的乘方法则和公式》
嘿,亲爱的小伙伴们!今天咱们来聊聊积的乘方法则和公式,这可是数学里超重要的一部分哟!
你知道吗?积的乘方就像是一场有趣的魔法表演。
比如说,(ab)ⁿ,这个式子就是积的乘方啦。
那它到底等于啥呢?告诉你哦,它就等于 aⁿbⁿ。
简单吧?
想象一下,这就好像是把一个大礼包拆开,里面的每一个小礼物都变得更精彩啦!比如(2×3)² ,按照咱们的法则,那就是
2²×3² ,也就是4×9 = 36 。
是不是很神奇?
而且啊,这个法则用处可大啦!当我们遇到那种一堆数字和字母相乘然后要乘方的时候,它就派上大用场啦。
比如说计算
(3x²y³)⁴,这要是一个个去乘,那得多麻烦呀。
但是有了积的乘方法则,那就轻松多啦,直接变成 3⁴×(x²)⁴×(y³)⁴,也就是
81x⁸y¹² 。
再说啦,学会这个法则,做数学题的时候就像是有了一把神奇的钥匙,能打开好多难题的锁。
比如说,在化简式子或者解方程的时候,它能让复杂的东西变得简单清晰,让我们一下子就能找到答案的方向。
还有哦,和小伙伴一起讨论数学问题的时候,你要是能熟练运用积的乘方法则,那可真是太酷啦,大家都会对你刮目相看的!
所以呀,小伙伴们一定要把这个积的乘方法则和公式牢牢记住哟,多做几道练习题,让它成为我们数学武器库里最厉害的法宝之一!加油,相信大家都能玩转这个有趣的法则,让数学变得更有趣!。
积的乘方法则和幂的乘方法则《积的乘方法则和幂的乘方法则积的乘方法则和幂的乘方法则》嘿,亲爱的小伙伴们!今天咱们来唠唠积的乘方法则和幂的乘方法则这两个数学里的重要宝贝!
先来说说积的乘方法则哈。
想象一下,有一堆数凑在一起相乘,然后要给它们整个次方,这时候该咋办呢?其实很简单,就把每个因数分别乘方,再把所得的幂相乘。
比如说,(ab)的 n 次方,那就等于 a 的 n 次方乘以 b 的 n 次方。
是不是有点像把大部队分成小队伍,各自行动,再汇总成果呀!
再瞅瞅幂的乘方法则。
要是一个幂自己又要乘方,那会咋样呢?嘿,这时候只要把指数相乘就行啦!比如说,(a 的 m 次方)的 n 次方,结果就是 a 的(m×n)次方。
这就好比给一个已经很厉害的力量再加上好几层功力,变得更强大!
这两个法则在数学里可重要啦!做题的时候,要是能熟练运用它们,那简直就像有了超级武器,难题都能被咱们轻松打败。
比如说算那种长长的式子,要是不知道这两个法则,那可就头大啦,像在迷宫里乱转。
但只要掌握了,就能一下子找到出口,轻松得出答案。
而且哦,这两个法则在生活中其实也有用呢!虽然可能不是那种直接能看出来的用处,但它们能锻炼咱们的脑子,让咱们变得更聪明,思考问题更有条理。
就像搭积木,知道了规则,就能搭出漂亮的城堡。
小伙伴们,别觉得数学法则枯燥无聊,它们就像隐藏在数字世界里的小魔法,只要咱们用心去发现,去掌握,就能在数学的大乐园里
玩得超级开心!加油哦,相信咱们都能把积的乘方法则和幂的乘方法则玩转,成为数学小达人!。
幂的乘方运算法则
底数不变,指数相乘。
即
a的m次幂的n次幂=a的(m?n)次幂(n、m为正整数)
积的乘方运算法则
把积的每个因式分别乘方,再把所得的幂相乘。
即
a、b乘积的n次方=a的n次方乘b的n次方(n为正整数)
幂的乘方与积的乘方运算法则
幂的乘方法则:幂的乘方是幂的一种运算积的乘方是指底数是乘积形式的乘方。
积的乘方法则:积的乘方,先把积中的每一个因数分别乘方,再把所得的幂相乘。
幂的乘方最终转化为指数的乘法运算,其中底数a可以是具体的数、单项式、多项式、分式乃至任何代数式。
幂的乘方是类比数的乘方,并借助于同底数幂的乘法性质来学习的,首先在具体例子的基础上抽象出幂的乘方的性质,进而通过推理加以论证,这一过程蕴含着转化及由特殊到一般,从具体到抽象的数学思想方法
幂的乘方与积的乘方运算法则
幂的乘方的运算法则:幂的乘方,低数不变,指数相加。
积的乘方的运算法则:是指底数是乘积形式的乘方。
积的乘方知识点总结一、乘方的基本概念1.1 乘方的定义乘方是指将一个数重复乘以自身多次的运算。
在乘方中,底数表示要重复乘的数,指数表示重复的次数。
乘方的一般形式可以表示为a^n,其中a为底数,n为指数,^表示乘方运算符。
1.2 指数的含义指数n表示底数a要连续乘以自身n次,比如a^2表示a乘以自身两次,a^3表示a乘以自身三次,依次类推。
指数n可以是正整数、负整数、零、分数或小数。
1.3 底数的含义底数a表示要重复乘的数,它可以是任意实数,包括正数、负数、零、分数或小数。
二、乘方的性质2.1 乘方的运算法则(1)指数为零的情况:任何数的零次方都等于1,即a^0=1(a≠0)。
(2)指数为正整数的情况:a的正整数次方表示a连续相乘n次。
(3)指数为负整数的情况:a的负整数次方表示a的倒数连续相乘n次,即a^(-n)=1/a^n。
(4)指数为分数或小数的情况:a的分数或小数次方表示a的n次方的开n次方,即a^(1/n)=n√a。
2.2 乘方的运算规律(1)同底数相乘:a^n×a^m=a^(n+m),即底数相同指数相加。
(2)同底数相除:a^n÷a^m=a^(n-m),即底数相同指数相减。
(3)幂的幂:(a^n)^m=a^(n×m),即多重乘方等于底数不变,指数相乘。
(4)零指数:a^0=1(a≠0)。
(5)负指数:a^(-n)=1/a^n。
2.3 乘方的特殊情况在乘方运算中,有一些特殊情况需要特别注意。
(1)底数为零的情况:对于零的乘方,考虑到零本身就是一个特殊的数,所以0^0没有定义。
(2)底数为1的情况:任何数的1次方都等于1,即1^n=1。
(3)底数为-1的情况:当指数是偶数时,(-1)^n=1;当指数是奇数时,(-1)^n=-1。
三、乘方的应用3.1 乘方在代数中的应用在代数中,乘方常常用来表示多项式、方程式、不等式等。
例如,a^n用来表示代数式a 的n次幂。
3.2 乘方在几何中的应用在几何中,乘方常常用来表示长度、面积、体积等。