中考数学总复习第一编教材知识梳理篇第6章图形的相似与解直角三角形阶段测评(六)试题
- 格式:pdf
- 大小:30.89 KB
- 文档页数:3


(完整)初三数学《相似三角形》知识点归纳(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)初三数学《相似三角形》知识点归纳(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)初三数学《相似三角形》知识点归纳(word版可编辑修改)的全部内容。
初三数学《相似三角形》知识提纲(孟老师归纳)一:比例的性质及平行线分线段成比例定理(一)相关概念:1.两条线段的比:两条线段的比就是两条线段长度的比在同一长度单位下两条线段a ,b 的长度分别为m ,n ,那么就说这两条线段的比是,或写成a :b=m :n ; 其中 a 叫做比的前项,b 叫做比的后项2:比例尺= 图上距离/实际距离3:成比例线段:在四条线段a ,b ,c ,d 中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段,记作:c d a b =(或a:b=c:d ) ① 线段a ,d 叫做比例外项,线段b ,c 叫做比例内项,② 线段a 叫首项,d 叫a ,b ,c 的第四比例项.③ 比例中项:若c a b c a b cb b a ,,2是则即⋅==的比例中项. (二)比例式的性质1.比例的基本性质:bc ad dc b a =⇔= 2.合比:若,则或a b c d a b b c d d a b a c d c =±=±±=± 3. 等比:若……(若……)a b c d e f m n k b d f n =====++++≠0则…………a c e m b d f n a b m n k ++++++++===4、黄金分割:把线段AB 分成两条线段AC,BC (AC>BC),并且使AC 是AB 和BC 的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中n m b a =AC=215-AB≈0.618AB,(三)平行线分线段成比例定理1.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。

知识点:一、比例线段1、比:选用同一长度单位量得两条线段。
a 、b 的长度分别是m 、n ,那么就说这两条线段的比是a :b =m :n (或nm b a =) 2、比的前项,比的后项:两条线段的比a :b 中。
a 叫做比的前项,b 叫做比的后项。
说明:求两条线段的比时,对这两条线段要用同一单位长度。
3、比例:两个比相等的式子叫做比例,如dc b a = 4、比例外项:在比例d cb a =(或a :b =c :d )中a 、d 叫做比例外项。
5、比例内项:在比例d cb a =(或a :b =c :d )中b 、c 叫做比例内项。
6、第四比例项:在比例dcb a =(或a :b =c :d )中,d 叫a 、b 、c 的第四比例项。
7、比例中项:如果比例中两个比例内项相等,即比例为abb a =(或a:b=b:c 时,我们把b 叫做a 和d 的比例中项。
8、比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么,这四条线段叫做成比例线段,简称比例线段。
9、比例的基本性质:如果a :b =c :d 那么ad =bc 逆命题也成立,即如果ad =bc ,那么a :b =c :d10、比例的基本性质推论:如果a :b=b :d 那么b 2=ad ,逆定理是如果b 2=ad 那么a :b=b :c 。
说明:两个论是比积相等的式子叫做等积式。
比例的基本性质及推例式与等积式互化的理论依据。
11、合比性质:如果d c b a =,那么d dc b b a +=+ 12.等比性质:如果n m d c b a ===K ,(0≠+++m d b Λ),那么ban d b m c a =++++++ΛΛ说明:应用等比性质解题时常采用设已知条件为k ,这种方法思路单一,方法简单不易出错。
13、黄金分割把一条线段分成两条线段,使较长的线段是原线段与较小的线段的比例中项,叫做把这条线段黄金分割。


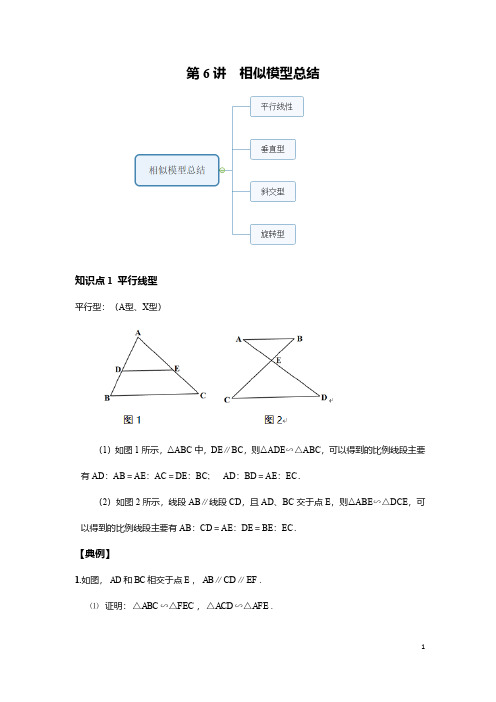
阶段测评(五) 图形的相似与解直角三角形(时间:60分钟,总分100分)一、选择题(每小题3分,共30分)1.(2018·临沂中考)如图,利用标杆BE 测量建筑物的高度.已知标杆BE 高1.2 m ,测得AB =1.6 m ,BC =12.4 m ,则建筑物CD 的高是( B )A .9.3 mB .10.5 mC .12.4 mD .14 m,(第1题图) ,(第3题图) ,(第4题图)2.(2018·滨州中考)在平面直角坐标系中,线段AB 两个端点的坐标分别为A (6,8),B (10,2),若以原点O 为位似中心,在第一象限内将线段AB 缩短为原来的12后得到线段CD ,则点A 的对应点C 的坐标为( C )A .(5,1)B .(4,3)C .(3,4)D .(1,5)3.(2018·宜宾中考)如图,将△ABC 沿BC 边上的中线AD 平移到△A ′B ′C ′的位置,已知△ABC 的面积为9,阴影部分三角形的面积为4.若AA ′=1,则A ′D 等于( A )A .2B .3 C.23 D.324.(2018·恩施中考)如图,在正方形ABCD 中,G 为CD 边的中点,连接AG 并延长交BC 边的延长线于点E ,对角线BD 交AG 于点F ,已知FG =2,则线段AE 的长度为( D )A .6B .8C .10D .125.(2018·荆门中考)如图,四边形ABCD 为平行四边形,E ,F 为CD 边的两个三等分点,连接AF ,BE 交于点G ,则S △EFG ∶S △ABG =( C )A .1∶3B .3∶1C .1∶9D .9∶1(第5题图) ,(第6题图) ,(第7题图)6.(2018·吉林中考)如图,将△ABC 折叠,使点A 与BC 边中点D 重合,折痕为MN .若AB =9,BC =6,则△DNB 的周长为( A )A .12B .13C .14D .157.(2018·长春中考)如图,某地修建高速公路,要从A 地向B 地修一条隧道(点A ,B 在同一水平面上).为了测量A ,B 两地之间的距离,一架直升机从A 地出发,垂直上升800 m 到达C 处,在C 处观察B 地的俯角为α,则A ,B 两地之间的距离为( D )A .800 sin α m ;B .800 tan α m C.800sin α m D.800tan αm8.如图,热气球的探测器显示,从热气球A 处看一栋楼顶部B 处的仰角为30°,看这栋楼底部C 处的俯角为60°,热气球A 处与楼的水平距离为120 m ,则这栋楼的高度为( A )A .160 3 mB .120 3 mC .300 mD .160 2 m,(第8题图) ,(第9题图) ,(第10题图)9.如图,在正方形ABCD 中,点E ,F 分别为BC ,CD 的中点,连接AE ,BF 交于点G ,将△BCF 沿BF 对折,得到△BPF ,延长FP 交BA 的延长线于点Q ,对于结论:①AE =BF ;②AE ⊥BF ;③sin ∠BQP =45;④S 四边形ECFG =2S △BGE ,其中正确的个数是(B )A .4B .3C .2D .110.如图,在Rt △ABC 中,AB =CB ,BO ⊥AC ,把△ABC 折叠,使AB 落在AC 上,点B 与AC 上的点E 重合,展开后,折痕AD 交BO 于点F ,连接DE ,EF .下列结论:①tan ∠ADB =2; ②图中有4对全等三角形;③若将△DEF 沿EF 折叠,则点D 不一定落在AC 上; ④BD =BF ; ⑤S 四边形DFOE =S △AOF ,上述结论中正确的个数是( B )A .4B .3C .2D .1 二、填空题(每小题4分,共20分)11.(2018·云南中考)如图,已知AB ∥CD ,若AB CD =14,则OA OC =__14__.(第11题图) (第12题图) (第13题图) (第14题图) (第15题图)12.(2018·潍坊中考)如图,一艘渔船正以60 n mile /h 的速度向正东方向航行,在A 处测得岛礁P 在东北方向上,继续航行1.5 h 后到达B 处,此时测得岛礁P 在北偏东30°方向,同时测得岛礁P 正东方向上的避风港M 在北偏东60°方向.为了在台风到来之前用最短时间到达M 处,渔船立刻加速以75 n mile /h 的速度继续航行__18+635__h 即可到达.(结果保留根号) 13.如图,AD 为△ABC 的角平分线,DE ∥AB 交AC 于点E ,如果AE EC =23,那么AB AC =__23__.14.如图,在边长相同的小正方形组成的网格中,点A ,B ,C ,D 都在这些小正方形的顶点上,AB ,CD 相交于点P ,则tan ∠APD 的值是__2__.15.如图,正方形ABCD 的边长为2,AE =EB ,MN =1,线段MN 的两端在CB ,CD 上滑动,当CM =__255或55__时,△AED 与以M ,N ,C 为顶点的三角形相似. 三、解答题(本大题4小题,共50分)16.(10分)如图,四边形ABCD 中,AD ∥BC ,点E 在CB 的延长线上,连接DE ,交AB 于点F ,连接DB ,∠AFD =∠DBE ,且DE 2=BE ·CE .(1)求证:∠DBE =∠CDE ;(2)当BD 平分∠ABC 时,求证:四边形ABCD 是菱形.证明:(1)∵DE 2=BE ·CE ,∴DE CE =BEDE. ∵∠E =∠E ,∴△DBE ∽△CDE . ∴∠DBE =∠CDE ;(2)∵∠DBE =∠CDE ,∠DBE =∠AFD ,∴∠CDE =∠AF D.∴AB ∥D C.又∵AD ∥BC ,∴四边形ABCD 是平行四边形.∴∠ADB =∠CB D. ∵BD 平分∠ABC ,∴∠CBD =∠AB D.∴∠ADB =∠AB D. ∴AB =A D.∴四边形ABCD 是菱形.17.(12分)如图是某小区入口抽象成的平面示意图.已知入口BC 宽3.9 m ,门卫室外墙AB 上的O 点处装有一盏路灯,点O 与地面BC 的距离为3.3 m ,灯臂OM 长为1.2 m (灯罩长度忽略不计),∠AOM =60°.(1)求点M 到地面的距离;(2)某搬家公司一辆总宽2.55 m ,总高3.5 m 的货车从该入口进入时,货车需与护栏CD 保持0.65 m 的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:3≈1.73,结果精确到0.01 m )解:(1)如图,过点M 作MN ⊥AB ,交BA 的延长线于点N . 在Rt △OMN 中,∠NOM =60°,OM =1.2, ∴∠M =30°.∴ON =12OM =0.6.∴NB =ON +OB =3.3+0.6=3.9. 即点M 到地面的距离是3.9 m ; (2)货车能安全通过. 取CE =0.65,EH =2.55, ∴HB =3.9-2.55-0.65=0.7.过点H 作GH ⊥BC ,交OM 于点G ,过O 作OP ⊥GH 于点P . ∵∠GOP =30°,∴tan 30°=GP OP =33.∴GP=33OP≈1.73×0.73≈0.40.∴GH≈3.3+0.40=3.70>3.5.∴货车能安全通过.18.(12分)(2018·衡阳中考)一名徒步爱好者来衡阳旅行,他从宾馆C出发,沿北偏东30°的方向行走2 000 m到达石鼓书院A处,参观后又从A处沿正南方向行走一段距离,到达位于宾馆南偏东45°方向的雁峰公园B处,如图.(1)求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离;(2)若这名徒步爱好者以100 m/min的速度从雁峰公园返回宾馆,那么他在15 min内能否到达宾馆?解:(1)如图,过点C作CD⊥AB于点D.∵∠A=∠ECA=30°,AC=2 000,∴CD=1 000.答:这名徒步爱好者从石鼓书院走到雁峰公园途中与宾馆之间的最短距离为1 000 m;(2)在Rt△CBD中,∠B=∠BCF=45°,CD=1 000,∴CB=2CD=1 0002,∴1 0002÷100=102<15,答:这名徒步爱好者15 min内能到达宾馆.19.(16分)(2018·邵阳中考)如图1,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.(1)证明:四边形OEFG是平行四边形;(2)将△OGE 绕点O 顺时针旋转得到△OMN ,如图2,连接GM ,EN . ①若OE =3,OG =1,求ENGM的值;②试在四边形ABCD 中添加一个条件,使GM ,EN 的长在旋转过程中始终相等.(不要求证明)(1)证明:如图1,连接A C.∵点O ,E ,F ,G 分别是AB ,BC ,CD ,AD 的中点, ∴OE ∥AC ,OE =12AC ,GF ∥AC ,GF =12A C.∴OE ∥GF ,OE =GF .∴四边形OEFG 是平行四边形;(2)解:①∵△OGE 绕点O 顺时针旋转得到△OMN ,∴OG =OM ,OE =ON ,∠GOM =∠EON . ∴OG OE =OM ON =13=33.∴△OGM ∽△OEN . ∴EN GM =OEOG= 3. ②(答案不唯一)如AC =B D.。
相似三角形一、知识概述1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。
2.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。
3.相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形.4.相似三角形的基本性质①相似三角形的对应边成比例、对应角相等.②相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
③相似三角形的周长比等于相似比④面积比等于相似比的平方温馨提示:①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例.②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽△ABC的相似比,当且仅当它们全等时,才有k=k′=1.③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出.5. 相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。
温馨提示:(1)判定三角形相似的几条思路:①条件中若有平行,可采用判定定理1;②条件中若有一对角相等(包括隐含的公共角或对顶角),可再找一对角相等或找夹边对应成比例;③条件中若有两边对应成比例,可找夹角相等;但是,在选择利用判定定理2时,一对对应角相等必须是成比例两边的夹角对应相等.④条件中若有等腰关系,可找顶角相等或底角相等,也可找腰和底对应成比例。
(2)在综合题中,注意相似知识的灵活运用,并熟练掌握线段代换、等比代换、等量代换技巧的应用,培养综合运用知识的能力。
(3)运用相似的知识解决一些实际问题,要能够在理解题意的基础上,把它转化为纯数学知识的问题,要注意培养当数学建模的思想。
相似三角形基本知识知识点一:放缩与相似1.图形的放大或缩小,称为图形的放缩运动。
2.把形状相同的两个图形说成是相似的图形,或者就说是相似性。
注意:⑴相似图形强调图形形状相同,与它们的位置、颜色、大小无关。
⑵相似图形不仅仅指平面图形,也包括立体图形相似的情况。
⑶我们可以这样理解相似形:两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到的. ⑷若两个图形形状与大小都相同,这时是相似图形的一种特例——全等形.3.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例。
注意:当两个相似的多边形是全等形时,他们的对应边的长度的比值是1.知识点二:比例线段有关概念及性质 (1)有关概念1、比:选用同一长度单位量得两条线段。
a 、b 的长度分别是m 、n ,那么就说这两条线段的比是a:b =m :n (或n m b a =)2、比的前项,比的后项:两条线段的比a:b 中.a 叫做比的前项,b 叫做比的后项. 说明:求两条线段的比时,对这两条线段要用同一单位长度.3、比例:两个比相等的式子叫做比例,如dc b a =4、比例外项:在比例dc b a =(或a :b =c :d )中a 、d 叫做比例外项. 5、比例内项:在比例d c b a =(或a :b =c:d)中b 、c 叫做比例内项。
6、第四比例项:在比例d cb a =(或a:b =c :d )中,d 叫a 、b 、c 的第四比例项。
7、比例中项:如果比例中两个比例内项相等,即比例为a bb a =(或a:b =b :c 时,我们把b 叫做a 和d 的比例中项。
8.比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即dcb a =(或a :b=c :d ),那么,这四条线段叫做成比例线段,简称比例线段.(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位)(2)比例性质1.基本性质: bcad d cb a =⇔= (两外项的积等于两内项积)2.反比性质: c da b dc b a =⇒= (把比的前项、后项交换)3。
精讲练习第六章 图形的相似与解直角三角形第十八讲 图形的相似 宜宾中考考情与预测近五年中考考情2021年中考预测年份 考查点 题型 题号分值 预计2021年宜宾中考考查在组合图形中,利用三角形相似知识,解决实际问题.xx三角形相似 选择题 73分 xx 三角形相似 填空题 15 3分 xx 三角形相似 填空题 16 3分 xx 位似 选择题 6 3分 xx三角形相似解答题2412分宜宾考题感知与试做1.(xx·宜宾中考)如图,△OAB 与△OCD 是以点O 为位似中心的位似图形,相似比为1∶2,∠OCD =90°,CO =CD.若B (1,0),则点C 的坐标为( B )A .(1,2)B .(1,1)C .(2,2)D .(2,1),(第1题图)),(第2题图))2.(宜宾中考)如图,在Rt △ABC 中,∠ACB =90°,∠A =30°,CD ⊥AB 于点D ,则△BCD 与△ABC 的周长之比为( A )A .1∶2B . 1∶3C . 1∶4D . 1∶53.(宜宾中考)若一个图形的面积为2,那么将与它成中心对称的图形放大为原来的两倍后的图形 面积为( A )A .8B .6C .4D .24.(xx·宜宾中考)如图,⊙O 的内接正五边形ABCDE 的对角线AD 与BE 相交于点G ,AE =2,则EG 的长是5-1 W.,(第4题图)) ,(第5题图))精讲练习5.(xx ·宜宾中考)如图,将△ABC 沿BC 边上的中线AD 平移到△A′B′C′的位置,已知△ABC 的面积为9,阴影部分三角形的面积为4.若AA′=1,则A′D 等于( A )A .2B .3C .23D .32宜宾中考考点梳理成比例线段、平行线分线段成比例1.两条线段的比是两条线段的长度之比. (1)两条线段的长度单位需统一; (2)线段的比是一个不带单位的数.2.成比例线段对于给定的四条线段a 、b 、c 、d ,如果其中两条线段的长度之比等于另外两条线段的长度之比,如a b =cd (或a∶b=c∶d),那么,这四条线段叫做成比例线段,简称比例线段.3.比例的性质基本性质:a b =cd ⇔ ad =bc (bd≠0).合(分)比性质:若a b =c d ,则a±b b = c±ddW.等比性质:若a b =c d =…=m n (b +d +…+n≠0),则a +c +…+m b +d +…+n = bW.4.黄金分割:如果点C 把线段AB 分成两条线段,使AC AB = AC ,那么点C 叫做线段AB 的 黄金分割点 ,AC 是BC 与AB 的比例中项,AC 与AB 的比值为5-12W. 5.平行线分线段成比例基本事实:两条直线被一组平行线所截,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.相似三角形6.相似三角形:对应边 成比例 、对应角 相等 的两个三角形叫做相似三角形,相似三角形对应边的比精讲练习叫做相似比.7.相似三角形的性质(1)相似三角形的对应角相等;(2)相似三角形的对应线段(边、高、中线、角平分线)成比例;(3)相似三角形的周长比等于相似比,面积比等于相似比的平方W.8.相似三角形的判定(1)两角分别相等的两个三角形相似;(2)两边成比例且夹角相等的两个三角形相似;(3)三边成比例的两个三角形相似;(4)平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似;(5)对于两个直角三角形,除了以上判定方法外,还可以通过得到:①一个锐角相等;②两组直角边对应成比例;③斜边和一直角边对应成比例来判定这两个直角三角形相似.相似多边形的判定及性质9.相似多边形:两个边数相同的多边形,如果各边对应成比例,各角对应相等,就称这两个多边形相似.10.相似多边形的性质(1)相似多边形的对应边成比例;(2)相似多边形的对应角相等;(3)相似多边形周长的比等于相似比,相似多边形面积的比等于相似比的平方W.位似图形11.位似图形:如果两个图形的对应点连线都交于一点,并且这一点到各组对应点的距离的比相等,那么这两个图形叫做位似图形,这个点叫做位似中心.【温馨提示】(1)位似图形上任意一对对应点到位似中心的距离之比等于相似比W.(2)在平面直角坐标系中,如果位似变换是以原点为中心,相似比为k,原图形上点的坐标为(x,y),那么位似图形上的点的坐标为(kx,ky)或(-kx,-ky)W.12.找位似中心的方法:将两个图形的各组对应点连接起来,若它们的直线或延长线相交于一点,则该点就是位似中心W.13.位似作图的步骤(1)确定位似中心、原图形的关键点、相似比(即要将图形放大或缩小的倍数);精讲练习(2)作出原图形中各关键点的对应点;(3)按原图形的连接顺序连接所作的各个对应点.1.(xx ·乐山中考)如图,DE ∥FG ∥BC ,若DB =4FB ,则EG 与GC 的关系是( B )A .EG =4GCB .EG =3GCC .EG =52GCD .EG =2GC2.(xx·内江中考)已知△ABC 与△A 1B 1C 1相似,且相似比为1∶3,则△ABC 与△A 1B 1C 1的面积比为( D )A .1∶1B .1∶3C .1∶6D .1∶93.(xx·资阳中考)已知:如图,△ABC 的面积为12,点D 、E 分别是边AB 、AC 的中点,则四边形BCED 的面积为 9 W.4.如图,四边形ABCD 和A′B′C′D′是以点O 为位似中心的位似图形,若 OA∶OA′=2∶3,则四边形ABCD 与四边形A′B′C′D′的面积比为( A )A .4∶9B .2∶5C .2∶3D .2∶3中考典题精讲精练线段成比例及比例的性质精讲练习【典例1】(1)若y x =34,则x +yx的值为( D )A .1B .47C .54D .74(2)下列各组线段(单位:cm )中,成比例线段的是( A )A .1,2,4,8B .2,4,6,8C .3,6,8,12D .3,6,9,12【解析】(1)∵y x =34,∴x +y x =4+34;(2)根据成比例线段的定义判断即可.位似变换【典例2】如图,△ABC 三个顶点坐标分别为A (-1,3),B (-1,1),C (-3,2).(1)请画出△ABC 关于y 轴对称的△A 1B 1C 1.(2)以原点O 为位似中心,将△A 1B 1C 1放大为原来的2倍,得到△A 2B 2C 2,请在第三象限内画出△A 2B 2C 2,并求出S △A 1B 1C 1∶S △A 2B 2C 2的值.【解析】(1)根据网格结构找出点A 、B 、C 关于y 轴的对称点A 1、B 1、C 1的位置,然后顺次连结即可得到△A 1B 1C 1;(2)连结A 1O 并延长至A 2,使A 2O =2A 1O ,连结B 1O 并延长至B 2,使B 2O =2B 1O ,连结C 1O 并延长至C 2,使C 2O =2C 1O ,然后顺次连结点A 2、B 2、C 2即可得到△A 2B 2C 2;由变换的方式可知△A 1B 1C 1与△A 2B 2C 2相似,且相似比为1∶2,根据相似三角形面积的比等于相似比的平方便可求出两个三角形的面积比.【解答】解:(1)△A 1B 1C 1如图所示; (2)△A 2B 2C 2如图所示.∵将△A 1B 1C 1放大为原来的2倍得到△A 2B 2C 2, ∴△A 1B 1C 1∽△A 2B 2C 2,且相似比为1∶2, ∴S △A 1B 1C 1∶S △A 2B 2C 2=1∶4.相似三角形的性质及判定精讲练习命题规律:在中考题目中,相似三角形的知识常与解直角三角形、全等三角形、圆、二次函数等知识综合.考查探索问题、解决问题的能力.【典例4】如图,在直角坐标系中,Rt △OAB 的直角顶点A 在x 轴上,OA =4,AB =3.动点M 从点A 出发,以每秒1个单位长度的速度,沿AO 向终点O 移动;同时点N 从点O 出发,以每秒1.25个单位长度的速度,沿OB 向终点B 移动.当两个动点运动了x s (0<x<4)时,解答下列问题:(1)求点N 的坐标;(用含x 的代数式表示)(2)在两个动点运动过程中,是否存在某一时刻,使△OMN 是直角三角形?若存在,求出x 的值;若不存在,请说明理由.【解析】(1)由勾股定理求出OB ,作NP⊥OA 于点P ,则NP∥AB,得出△OPN∽△OAB,得出比例式,求出OP 、PN ,即可得出点N 的坐标;(2)分两种情况:①若∠OMN=90°,则MN∥AB,由平行线得出△OMN∽△OAB ,得出比例式,即可求出x 的值;②若∠ONM =90°,则∠ONM =∠OAB ,证出△OMN∽△OBA,得出比例式,求出x 的值即可.【解答】解:(1)根据题意,得MA =x ,ON =1.25x , 在Rt △OAB 中,由勾股定理,得OB 2=OA 2+AB 2, OB =OA 2+AB 2=42+32=5.作NP⊥OA 于点P ,如图①, 则NP∥AB,∴△OPN ∽△OAB , ∴PN AB =OP OA =ONOB, 即PN 3=OP 4=1.25x 5, 解得OP =x ,PN =34x ,∴点N 的坐标是⎝ ⎛⎭⎪⎫x ,34x ;精讲练习(2)存在某一时刻,使△OMN 是直角三角形.理由:①若∠OMN=90°,如图②,则MN ∥AB ,此时OM =4-x ,ON =1.25x.∵MN ∥AB ,∴△OMN ∽△OAB ,∴OM OA =ON OB ,即4-x 4=1.25x 5, 解得x =2;②若∠ONM=90°,如图③,则∠ONM=∠OAB,此时OM =4-x ,ON =1.25x.∵∠ONM=∠OAB,∠MON =∠BOA,∴△OMN ∽△OBA ,∴OM OB =ON OA ,即4-x 5=1.25x 4,解得x =6441. 综上所述,x 的值是2或6441 时,△OMN 是直角三角形.1.下列各组数中,成比例的是( A )A .-6,-8,3,4B .-7,-5,14,5C .3,5,9,12D .2,3,6,122.如图,直线l 1∥l 2∥l 3,直线AC 分别交l 1、l 2、l 3于点A 、B 、C ;过点B 的直线DE 分别交l 1、l 3于点D ,E.若AB =2,BC =4,BD =1.5,则线段BE 的长为( C )A .1B .2C .3D .4精讲练习3.已知a b =34,b c =35,则a∶b∶c 等于( C )A .3∶4∶5B .4∶3∶5C .9∶12∶20D .9∶15∶204.如图,△OAB 与△OCD 是以点O 为位似中心的位似图形,相似比为1∶2,∠OCD =90°,CO =CD ,若B (1,0),则点C 的坐标为( D )A .(1,-2)B .(-2,1)C .(2,-2)D .(1,-1),(第4题图)),(第5题图))5.如图,以点O 为位似中心,将△ABC 放大得到△DEF,若AD =OA ,则△ABC 与△DEF 的面积之比为 1∶4 W.6.如图,直线y =12x +1与x 轴交于点A ,与y 轴交于点B ,△BOC 与△B′O′C′是以点A 为位似中心的位似图形,且相似比为1∶3,求点B 的对应点B′的坐标.解:∵直线y =12x +1与x 轴交于点A ,与y 轴交于点B.令x =0,可得y =1, 令y =0,解得x =-2,∴点A 和点B 的坐标分别为(-2,0),(0,1).∵△BOC 与△B′O′C′是以点A 为位似中心的位似图形,且相似比为1∶3, ∴OB O′B′=13,∴O ′B ′=3, ∴点B′的坐标为(-8,-3)或(4,3).7.△ABC 与△DEF 的相似比为1∶4,则△ABC 与△DEF 的周长比为( C )A .1∶2B .1∶3C .1∶4D .1∶16精讲练习8.如图,在平行四边形ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF ∶FC 等于( D )A .3∶2B .3∶1C . 1∶1D .1∶29.在下列命题中,真命题是( D ) A .两个钝角三角形一定相似 B .两个等腰三角形一定相似 C .两个直角三角形一定相似 D .两个等边三角形一定相似10.梯形的中位线长为12 cm ,上、下底之比为1∶3,则梯形的上、下底之差是 -12 W.11.如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点,DE ∥BC ,BE 与CD 相交于点F ,则下列结论一定正确的是( A )A .AD AB =AE AC B .DF FC =AE ECC .AD DB =DE BC D .DF BF =EF FC12.(xx ·宜宾模拟)如图,在矩形ABCD 中E 是AD 边的中点,BE ⊥AC ,垂足为F ,连结DF ,下列四个结论:①△AEF∽△CAB;②tan ∠CAD =2;③DF=DC ;④CF=2AF ,正确的是( C )A .①②③B .②③④C .①③④D .①②④精讲练习【感谢您的阅览,下载后可自由复制或修改编辑,敬请您的关注】。