范德华半径无机化学精品课程

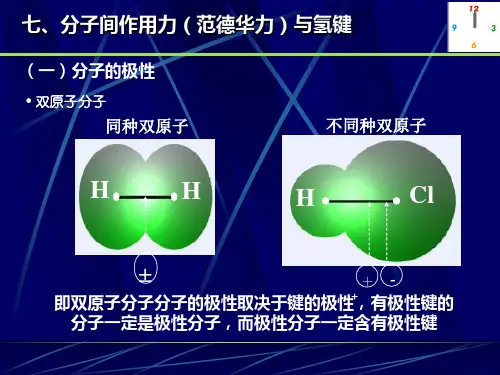
专题4.范德华力Van der Waals' force一、次级键secondary bond1.concept次级键，除了典型的强化学键(共价键、离子键和金属键)等，依靠氢键以及弱的共价键和范德华 作用力相结合的各种分子内和分子间作用力的总称；2.次级键可根据原子间的距离、核磁共振谱和光谱等实验数据来确定；化学反应过程中形成的过渡态正是以次级键为特征的中间体或活化络合体； 次级键在物质的结构和性质的研究以及生物体系和超分子化学中起重大作用；3.反映在分子结构上，当原子间距离小于或接近相应的离子半径、共价半径或金属半径之和时， 可以认为原子间形成了化学键；当不同分子中的原子间距离范德华半径之和时，可以认为分子间存在着范德华力； 当原子间距离介于化学键与范德华力范围之间时，可以认为原子间生成次级键；4.次级键普遍客观存在，且化学键、次级键和范德华力三者之间的界限是很难明确划分；5.次级键中有相当一部分是有氢原子参与的；氢键(hydrogen bond )是次级键的一个典型，也是最早发现和研究的次级键；二、范德华半径V an der Waals radius1.concept:非金属元素有一种半径，叫范德华半径；原子的范德华半径是指当分子中两个相邻但不成键的原子靠近至一定距离时，可设想原子本身 的排斥力范围为一刚性球体，这一球体的半径称为范德华半径；2.如图表示出2个Cl 2，在同一个Cl 2里，2个Cl 核间距的一半是共价半径共r ； 在不同的2个Cl 2间，2个Cl 的核间距的一半是范氏半径范r ，显而易见共r <范r ；3.区别与联系①一般来说，对于金属元素，只有共价半径和金属半径； ②非金属元素(稀有气体除外)有共价半径和范德华半径； ③稀有气体元素只有范德华半径；④高中教材上原子半径全部用的是共价半径，所以稀有气体元素与同周期其它元素没有可比性；三、偶极dipole1.concept ：偶极---表示分子的极性；2.偶极可以分为三类：①固有偶极：极性分子中由于组成元素不同，其吸引电子的能力各有差异(元素周期律)，这就使 得分子中有电子偏移的现象，这样就产生了极性，并且偶极持续存在，称为固有偶极；-+δδCl H —②诱导偶极：是指非极性分子在电场中或者有其他极性分子在较近距离的情况下，由于电子带 负电，核带正电，它们会发生偏移，这种现象称为诱导偶极；③瞬时偶极：一切分子中，不管是极性分子还是非极性分子，原子核时刻在震动，电子时刻在 运动、跃迁，在它们运动的时候，偶尔离开平衡位置而产生极性，只不过这个过程持续时间 很短，故称瞬时偶极；四、偶极矩dipole moment1.concept正、负电荷中心间的距离和电荷中心所带电量的乘积，它是一个矢量，方向规定为从正电中心 指向负电中心，用符号μ表示，单位为库伦·米(C·m )； ①当一个电量(C e 19106022.1-⨯=)的正、负电荷相距m 1010-，则其偶极矩为： m C ⋅⨯=-29106022.1μ；②在静电制中，上述偶极矩为deb esu cm 8.4108.418=⋅⨯=-μ；③德拜是偶极矩的另一种单位，两者之间的换算为：m C deb ⋅⨯=-3010336.31； 2.偶极矩的数学表达式为μ=qd ；3.应用：①衡量键的极性强弱⎪⎩⎪⎨⎧≠=越大，键的极性越强，极性共价键，非极性共价键μμμ00【键的偶极矩简称键矩】A -B 键矩/deb A -B 键矩/debA -B 键矩/deb H -C 0.4 C -C 0 N -F 0.17 H -N 1.31 C -N 0.22 C =C 0 H -O 1.51 C -O 0.74 C =N 0.9 H -S 0.68 C -S 0.9 C =O 2.3 H -Cl 1.08 C -F 1.41 C =S 2.6 H -Br 0.78 C -Cl 1.46 N =O 2.0 H -I 0.38 C -Br 1.38 P =O 2.7 H -P 0.36 N -O 0.3 S =O 3.0②判断多原子分子极性强弱⎪⎩⎪⎨⎧≠=越大，分子的极性越强，分子是极性分子，分子是非极性分子μμμ00分子 μ/(m C ⋅-3010))10/(10m r - )10/(30m C er ⋅- er /μ CO 0.39 1.1283 18.08 0.02 HF 6.37 0.9168 14.69 0.43 HCl 3.50 1.2744 20.42 0.18 HBr 2.64 1.4145 22.66 0.12 HI1.271.6090 25.780.05五、范德华力V an der Waals' force1.concept范德华力(又称分子作用力)产生于分子或原子之间的静电相互作用；范德华力偶极子电荷位移近邻原子相互作用电偶极矩的感应作用−−−−−→−→→)(dipoles 2.范德华力又可以分为三种作用力：诱导力、色散力和取向力；①色散力dispersion force 【非极性分子间形成】※色散力(也称“伦敦力”，London force )是指非极性分子相互靠拢时，它们的瞬时偶极矩之间 产生的很弱的吸引力，所有分子或原子间都存在；※是分子的瞬时偶极间的作用力，即由于电子的运动，瞬间电子的位置对原子核是不对称的， 也就是说正电荷重心和负电荷重心发生瞬时的不重合，从而产生瞬时偶极；※色散力和相互作用分子的变形性有关，变形性越大(分子量愈大，变形性愈大)色散力越大； ※色散力和相互作用分子的电离势(即为电离能)有关，分子的电离势越低(分子内所含的电子数 愈多)，色散力越大；※色散力的相互作用随着61r 而变化；其公式为：I 1和I 2 分别是两个相互作用分子的电离能，α1和α2 是它们的极化率；206212121d )4(123E πεααr I I I I +-= ※色散力是菲列兹·伦敦(Fritz London )于1930年根据近代量子力学方法证明的，由于从量子 力学导出的理论公式与光色散公式相似，因此把这种作用称为色散力，又叫做伦敦力； ②诱导力induction force 【极性与非极性分子间或极性分子间形成】※诱导力在极性分子和非极性分子之间或极性分子和极性分子之间都存在诱导力； ※由于极性分子偶极所产生的电场对非极性分子发生影响，使非极性分子电子云变形(即电子云 被吸向极性分子偶极的正电的一极)，结果使非极性分子的电子云与原子核发生相对位移，本 来非极性分子中的正、负电荷重心是重合的，相对位移后就不再重合，使非极性分子产生了 偶极；※这种电荷重心的相对位移叫做“变形”，因变形而产生的偶极，叫做诱导偶极，以区别于极 性分子中原有的固有偶极；※诱导偶极和固有偶极就相互吸引，这种由于诱导偶极而产生的作用力，叫做诱导力；※在极性分子和极性分子之间，除了取向力外，由于极性分子的相互影响，每个分子也会发生 变形，产生诱导偶极；其结果使分子的偶极距增大，既具有取向力又具有诱导力； ※在阳离子和阴离子之间也会出现诱导力； ※诱导力与极性分子偶极矩的平方成正比；※诱导力与被诱导分子的变形性成正比，通常分子中各原子核的外层电子壳越大(含重原子越多)它在外来静电力作用下越容易变形；相互作用随着61r而变化，诱导力与温度无关；其公式：α为极化率；620212)4(rE πεμα-=诱 ③取向力dipole-dipole force 【极性分子间形成】 ※取向力发生在极性分子与极性分子之间；※由于极性分子的电性分布不均匀，一端带正电，一端带负电，形成偶极；因此，当两个极性 分子相互接近时，由于它们偶极的同极相斥，异极相吸，两个分子必将发生相对转动；这种 偶极子的互相转动，就使偶极子的相反的极相对，叫做“取向”；这时由于相反的极相距较 近，同极相距较远，结果引力大于斥力，两个分子靠近，当接近到一定距离之后，斥力与引 力达到相对平衡；这种由于极性分子的取向而产生的分子间的作用力，叫做取向力； ※取向力与分子的偶极矩平方(μ)成正比，即分子的极性越大，取向力越大； ※温度越高，极性分子运动越活跃，越不容易取向，取向力越弱；其公式为：0622214132E πεμμkTr -=取 μ1，μ2为两个分子的偶极矩；r 为分子质心间的距离，k 为Boltzmann 常数，T 为热力学温度， 负值表示能量降低； ④三种力的关系※极性分子与极性分子之间，取向力、诱导力、色散力都存在； ※极性分子与非极性分子之间，则存在诱导力和色散力； ※非极性分子与非极性分子之间，则只存在色散力；※这三种类型的力的比例大小，决定于相互作用分子的极性和变形性； ※极性越大，取向力的作用越重要；变形性越大，色散力就越重要；※诱导力则与这两种因素都有关；但对大多数分子来说，色散力是主要的； ※只有偶极矩很大的分子(如水)，取向力才是主要的；而诱导力通常是很小的； ※极化率α反映分子中的电子云是否容易变形；※虽然范德华力只有0.4~4.0kJ/mol ，但是在大量大分子间的相互作用则会变得十分稳固；。

（完整版）⽆机化学（天津⼤学版）第⼀章化学反应中的质量关系和能量关系[学习指导]1．“物质的量”（n）⽤于计量指定的微观基本单元或其特定组合的物理量，其单位名称为摩[尔]，单位符号为mol。

2.摩尔质量（M) M = m/n3.摩尔体积（V m）V m = V/n4.物质的量浓度（c B）c B = n B/V5.理想⽓体状态⽅程pV = nRT6.理想⽓体分压定律p= Σp B ；p B = (n B/n)p7.化学计量式和化学计量数O = ΣνB B ；νBB8.反应进度（ξ）表⽰化学反应进⾏程度的物理量，符号为ξ，单位为mol。

随着反应的进⾏，任⼀化学反应各反应物及产物的改变量：Δn B = νBξ9.状态函数状态函数的改变量只与体系的始、终态有关，⽽与状态变化的途径⽆关。

10.热和功体系和环境之间因温差⽽传递的热量称为热。

除热以外，其它各种形式被传递的能量称为功。

11.热⼒学能（U）体系内部所含的总能量。

12.能量守恒定律孤⽴体系中能量是不会⾃⽣⾃灭的，它可以变换形式，但总值不变。

13.热⼒学第⼀定律封闭体系热⼒学能的变化：ΔU = Q + WQ > 0, W > 0, ΔU > 0；Q < 0, W< 0, ΔU < 0。

14.恒压反应热（Q p）和反应焓变（Δr H m）H(焓) ≡ U + pV, Q p= Δr H m15.赫斯定律Q p= ∑Q B, Δr H m= ∑Δr H m(B)B B16.标准状况：p = 101.325kPa, T = 273.15 K标准(状)态：pθ= 100kPa下⽓体：纯⽓体物质液体、固体：最稳定的纯液体、纯固体物质。

溶液中的溶质：摩尔浓度为1mol·L-1标准态下17.标准摩尔⽣成焓（）最稳定的单质─────—→单位物质的量的某物质=18.标准摩尔反应焓变（）⼀般反应cC + dD = yY + zZ=[y(Y) + z(Z)] - [c(C)+ d(D)]=Σνi(⽣成物) + Σνi(反应物)第⼆章化学反应的⽅向、速率和限度[学习指导]1.反应速率：单位体积内反应进⾏程度随时间的变化率，即：2.活化分⼦：具有等于或超过E c能量（分⼦发⽣有效碰撞所必须具备的最低能量）的分⼦。

第1次课学时 2及发射卫星使用的高能燃料。

4.计算机中信息存储设备。

化学在畜牧生产中的作用：生物体本身就是多种化合物组成的集合体，如：细胞，线粒体，溶酶体等等。

当今科技已发展到从分子水平上研究生物科学，产生了分子生物学等新型学科。

生物学的研究越来越离不开化学原理、化学知识和化学分析技术。

二、讲授新课：第一节原子结构元素周期系一、原子核外电子的运动状态（一）、微观粒子的统计规律性1.微观粒子的波粒二象性结论：正是由于微观粒子与宏观粒子不同，不遵循经典力学规律，而要用量子力学来描述它的运动状态。

电子衍射示意图2.测不准原理图△X·△P≥h/4π（二）、波函数和原子轨道薛定谔方程：描述核外电子运动的波动方程。

薛定谔方程是描述微观粒子运动状态、变化规律的基本方程。

它的解并不是具体的数资，而是一个含有三个变量x、y、z和三个参数n、l、m的函数式，叫做波函数ψ，表示为ψ(x，y，z)。

波函数是描述核外电子运动状态的数学函（15分钟）微观粒子的统计规律性（20分钟）波函数和原子轨道数式。

量子力学中的原子轨道不是某种确定的轨道，而是原子中一个电子可能的空间运动状态，包含电子所具有的能量，离核的平均距离、几率密度分布等。

（三）、几率密度和电子云电子在核外空间某处单位微小体积内出现的几率，称为几率密度，用波函数绝对值的平方|ψ|2表示。

常常形象地将电子的几率密度(|ψ|2)称作“电子云”。

1s电子云界面图电子云的角度分布图（四）、四个量子数及其对核外电子运动状态的描述1.主量子数(n)（1）取值范围它只能取1，2，3……等正整数。

（2）物理意义：①主量子数n是决定电子能量的主要因素。

②主量子数表示电子离核的远近或电子层数。

在光谱学上常用一套拉丁字母表示电子层，常用K、L、M、N、O、P、Q等符号分别表示n = 1，2，3，4，5，6，7。

2.角量子数(l) （10分钟）几率密度和电子云（30分钟）四个量子数图原子轨道的角度分布图第2次课学时 2一、课程回顾：（和同学们互动，以提问的方式回忆上节课所讲内容并板书）一、原子核外电子的运动状态（一）、微观粒子的统计规律性（二）、波函数和原子轨道（三）、几率密度和电子云（四）、四个量子数及其对核外电子运动状态的描述提问并讲解：二、讲授新课：二、原子核外电子的排布（一）、核外电子排布的规律1.保里(Pauli)不相容原理2.能量最低原理3.洪特(Hund)规则（二）、近似能级图学时 2图 稀溶液的沸点升高、凝固点下降AB 为纯水的蒸气压曲线，A′B′为稀溶液的蒸气压曲线，AC 为冰的蒸气压曲线溶液的沸点上升：B b b b b b K T T T ⋅=-=∆ο凝固点下降：B f f f f b K T T T ⋅=-=∆ο3、溶液的渗透压半透膜： 渗透压：课程小结：。

范德华半径详细资料大全
原子的范德华半径是指在分子晶体中，分子间以范德华力（分子间存在的一种吸引力）结合，以稀有气体为例，相邻两原子核间距的一半，即为范德华半径。

基本介绍
•中文名：范德华半径
•属性：非金属元素有一种半径
•又称：范氏半径
•实列：稀有气体的分子晶体相邻两原子核间距的一半
范氏（范德华）半径非金属元素有一种半径，叫范氏半径．例如，在CdCl2晶体里，测得在不同的“分子”（实际是层状的大分子）里Cl与Cl间的核间距为：d(Cl-Cl)=0.376nm．取其值的一半定为氯原子的范氏半径，即：r范=1/2(0.376nm)=0.188nm．对非金属元素，总有r范>r共，从上图可以清楚地看出这一关系．图中表示出2个Cl2，在同一个Cl2里，2个Cl核间距的一半是共价半径r共；在不同的2个Cl2间，2个Cl的核间距的一半是范氏半径r范．显而易见，r 范>r共．一般来说，对于金属元素，只有共价半径和金属半径；而非金属元素（稀有气体除外）有共价半径和范氏半径；稀有气体元素只有范氏半径．高中教材上原子半径全部用的是共价半径，所以稀有气体元素的半径与同周期其它元素没有可比性．。

无机化学精品教案（全套）第一章物质的状态§ 1-1 气体一、理想气体状态方程式理想气体的条件是:分子本身不占体积,分子间没有相互作用力,分子和分子之间、分子和器壁之间的碰撞是完全弹性的。

理想气体状态方程式: pV=nRT由于n=m / M(m为理想气体质量,M为摩尔质量),所以上式可改写成pV=RT又因为气体的密度ρ =m / V ,式上式又可改写成pM=ρRT 使用理想气体状态方程式,应注意两点: ⑴它只适用于理想气体,对实际气体仅在高温、低压下近似适用。

⑵注意单位的匹配。

摩尔气体常数R在p和V单位不同时,应选用相应的单位,例如:8.314 Pa?m3?mol-1?K-1;8.314 kPa?L?mol-1?K-1;8.314 J?mol-1?K-1。

二、气体分压定律1.基本概念分压力恒温时,某组分气体占据与混合气体相同体积时所产生的压力分体积恒温时,某组分气体具有和混合气体相同压力时所占有的体积2.混合气体中某组分气体的气态方程式piV总 = n i RT 或 p总Vi = n i RT注意:用总体积时则乘以分压力;而用总压力时则乘以分体积。

3.气体分压定律文字表述混合气体的总压力等于各组分气体分压力之和;某组分气体分压力的大小和它在气体混合物中的体积分数(或摩尔分数)成正比。

数学表达式 p总 = p1 + p2 +p3 …… + pi = ∑pipi= ×p总或pi = ×p总4.气体分压定律的应用计算混合气体中某组分的分压力;改正在水面上收集气体的真正压力。

三、气体扩散定律文字表述同温同压下,气体的扩散速度与其密度(或摩尔质量)的平方根成反比。

数学表达式定律的应用根据分子量计算不同气体间的扩散速度比;由已知分子量和扩散速度比,计算未知气体的分子量。

四、实际气体状态方程式1.实际气体与理想气体的偏差实际气体分子本身有一定体积,所以其真正体积比表观的体积小; 实际气体分子间有相互作用力,因此其真正压力比表观的压力大。

区别金属原子半径、离子半径、共价半径和范德华半径根据量子力学，核外电子运动没有固定轨道，没有明确的界限，只有几率密度的分布。

通常把核到最外层电子的平均距离定义为原子半径。

现代的科学技术还无法精确测定一个单独原子的半径，只能用实验方法，如X射线衍射法，测定出晶体中相同原子核间距离，或用同核双原子分子键长，被2相除得出。

不同元素原子有不同的存在形式，就是同一元素的原子也可能形成不同化学键的分子和晶体。

因而不同元素的原子半径可能表现形式不同，就是同一元素的原子半径也可能有不同形式。

根据测定方法的不同，通常有3种原子半径：①金属半径：金属晶体中相邻两金属原子核间距离的一半，称做该元素原子的金属半径，如铜的金属半径r金＝127.8pm。

②共价半径：同种元素的两原子以共价键结合时，其共价键键长的一半称做该元素原子的共价半径，符号表示为pm 或Å，其数值与几重键结合有关，如碳原子的共价半径r共，单键时为77pm，双键时为67pm，三键时为60pm。

金属元素原子在一定条件下也可形成共价的双原子分子，金属元素原子也有共价半径，如铜的共价半径r共为117pm。

由于形成共价键时，总会发生原子轨道重叠，通常同一金属元素的金属半径比其单键共价半径要大10%～15%。

同周期元素的单键共价半径的变化规律为从左至右逐渐缩小，可认为是原子核对电子引力增大的缘故③范氏半径：(范德华氏半径的简称) 非金属元素和有些金属元素所形成的分子间或稀有气体单原子分子间靠分子间力(范德华力) 相互吸引，其不同分子中两个相同原子核间距离的一半，称做该元素原子的范氏半径，如氯原子的范氏半径r范为181pm。

如左图所示，表示了氯原子的共价半径和范氏半径。

原子半径数据只有相对的、近似的意义，而且同一元素的不同半径，数值不同(r范>r金>r共)，而且相差较大。

使用时不要同时用不同半径的数据。

在一般的资料里，金属元素有金属半径和共价半径的数据，非金属元素则有共价半径和范氏半径的数据，稀有气体只有范氏半径的数据。