高级微观经济学(上海财经大学 陶佶)note01
- 格式:pdf
- 大小:183.70 KB
- 文档页数:12





三、The Consumer ’s Problem本部分考察消费者选择理论的其他组成要素:Consumption Set 、Feasible Set 、Behavior Assumption ,然后构建消费者选择理论的正式表述。
Assumption1.2消费者偏好:消费者偏好关系具有完备性、传递性、严格单调性和严格凸的,那由定理1.1和1.3可知,该偏好关系可以有一个连续的、严格增加的、严格拟凹的实值效用函数u 代表。
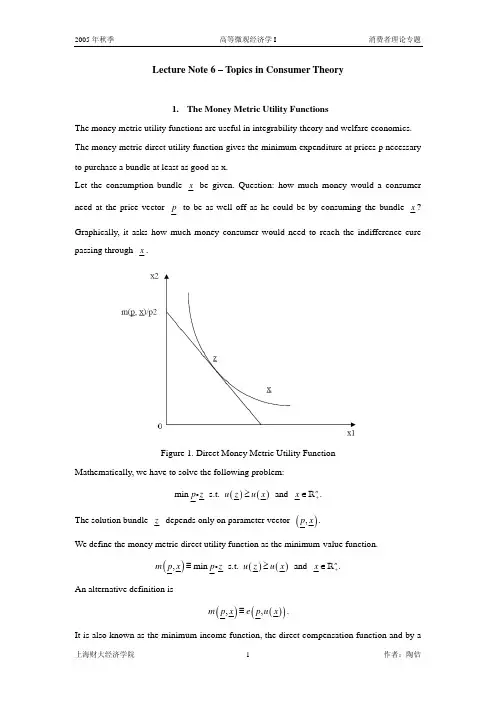
(考察两种商品情形) 消费者的行为假设:假设消费者根据其偏好关系在可行集中选择最偏好的消费束,即消费者选择能够支付得起的最优商品组合,即:*B ∈x ,使得对于所有的B ∈x ,有*x x f % (1.4) “支付得起”——预算集“最优”——偏好关系 预算集:{}R ,,0,0nB y y +=∈≤>>≥x x px p⏹ 消费者从预算集中选择最偏好的商品组合(点)*x : *B ∈x ,且对于所有的B ∈x ,有*x x f %。
⏹ 消费者从预算集中选择最大化效用函数的点*x : ()()()**arg max ,..u u u s t y ⇓≥=≤x x x x px 144444424444443给定假设1.2,并给定对消费者可行集的限制, 消费者问题(1.4)⇔受到约束的效用函数最大化问题; 即消费者问题转化为下面的优化问题:()1max ,..ni i i u B s t y p x y=∈≤⇒≤∑x x px (1.5) 接着需要考虑的问题是:此最大化问题是否有解? 是否有唯一解?定理A1.10:极值的存在性定理(解决了解的存在性问题) 设R nS +∈是非空紧集,:R f S →是连续的实值映射,则存在向量*S ∈x 和向量S ∈x %,对于所有的S ∈x ,有()()()*f f f ≤≤x x x % 该定理在(1.5)问题的应用:()u x 连续 {}R ,,0,0n B y y +=∈≤>>≥x x px p :非空、闭集、有界集 (其中,闭集+有界集⇒紧集)定理A2.14:目标函数严格凹(解决了解的唯一性问题)如果*x 最大化严格凹函数f ,那么*x 就是该函数唯一的全局最大值点; 如果*x 最小化严格凸函数f ,那么*x 就是该函数唯一的全局最大值点; 定理1.4:消费者效用最大化问题一阶条件的充分性假设()u x 是R n +上的连续拟凹函数,而且(p,y)0>>,如果u 在*x 处可微,而且**(x ,)0λ>>满足效用最大化问题的一阶条件(1.10),那么*x 就是使得消费者在价格p 和收入y 处达到效用最大化的解。





Chapter 1: Introductionz How to build an economic model? (Hal R.Varian)1. An economic model: an idealization of the reality, but not the reality.2. Why do we need an economic model?3. How to build an economic model? z Getting ideas from reality: An interesting one? Is the idea worth pursuing? z Don’t look at the literature too soon z Simplifying and Generalizing your model z Making mistakes: team work z Searching the literature z Giving a seminar1z Mathematics 1. Set theoryA Set (A) is a collection of objects called elements (a): a ∈ A The empty set is Φ , and the universal set is U .Binary operations on set: 1. 2. 3. 4. the union of A and B is the set A ∪ B = {x : x ∈ A or x ∈ B} the intersection of A and B is A ∩ B = {x : x ∈ A and x ∈ B} the difference of A and B isA \ B = {x : x ∈ A and x ∉ B}the symmetric difference of A and B is A∆B = ( A ∪ B ) \ ( A ∩ B )The complement of A is Ac = U \ ATheorem 1Let A, B and C be sets,1. 2.A \ (B ∪ C ) = ( A \ B ) ∩ ( A \ C ) A \ (B ∩ C ) = ( A \ B ) ∪ ( A \ C )ACBCorollary 2 (DeMorgan’s Law)( A ∪ B )c = Ac ∩ B cand ( A ∩ B ) = Ac ∪ B cc2Generalizing theorem 1 to theorem 3: A\⎛ ⎜ ∪ Si ⎞ ⎟ = ∩( A \ S i ) and A \ ⎛ ⎜ ∩ Si ⎞ ⎟ = ∪( A \ S i ) ⎝ i∈I ={1, 2,3...} ⎠ i∈I ⎝ i∈I ={1, 2,3...} ⎠ i∈IGiven any set A, the power set of A, written by Ρ( A) is the set consisting of all subsets of A, i.e., Ρ( A) = {B | B ⊂ A}Question : If a set A has n elements, how many elements are there in Ρ( A) ?The Cartesian Product of two sets A and B (also called the product set or cross product) is defined to be the set of all points (a, b ) where a ∈ A and b ∈ B . It is denoted A × B .Example:R2 ≡ R × RR n ≡ R × R × R × ...R = {( x1 , x2 ,..., xn ) | xi ∈ R, i = 1,2,...n} ,wheretheelement(x1 , x2 ,...xn ) ofR n is an n-dimensional ordered vector. We denote: xS ⊂ R n is a convex set if ∀x, y ∈ S , we have tx + (1 − t ) y ∈ S for all t ∈ [0,1]The intersection of convex sets is convex, but the union of them is not.32. TopologyA metric space is a set S with a global distance function (the metric d ) that, for every pointsx and y in S , gives the distance between them as a nonnegative real number d (x, y ) . Ametric space must satisfy: 1. d (x, y ) = 0 iff x = y 2. d (x, y ) = d ( y, x ) 3. d ( x, y ) + d ( x, z ) ≥ d (x, z ) Example: Euclidean metric in R 2 : d (x, y ) =(x1 − y1 )2 + (x2 − y2 )2Open and Closed ε − Balls: let ε be a real positive number, then 1. The open ε − ball with center x 0 and radius ε > 0 isBε x 0 = x ∈ R n | d x 0 , x < ε( ) {() }) }2. The closed ε − ball with center x 0 and radius ε > 0 isBε x 0 = x ∈ R n | d x 0 , x ≤ ε( ) {(Open and Closed sets in R n : A set S ⊂ R n is open if ∀x ∈ S , ∃ε > 0,Bε ( x ) ⊂ S .A set S ⊂ R n is closed if its complement, S c , is open.Some important properties of open and closed sets: 1. The union of open sets is open. 2. The intersection of any finite number of open sets is open. 3. The union of any finite number of closed sets is closed.44. The intersection of closed sets is closed.Question: what if the collection is infinite for 2. and 3.?Theorem 4: Every open set is a collection of open balls.Bounded sets in R n : A set S ⊂ R n is bounded if ∃ε > 0 and x ∈ R n , S ⊂ Bε ( x ) .Let S ⊂ R be a nonempty set of real numbers: 1. Any real number l is a lower bound if ∀ x ∈ S , 2. Any real number u is an upper bound if ∀ x ∈ S ,x ≥ l . The set is bounded from below. x ≤ u . The set is bounded from above.3. The largest number among lower bounds is called the greatest lower bound of S. 4. The smallest number among upper bounds is called the least upper bound of S.A bounded set is bounded both from below and above. We can show that for any bounded subsets of the real line, there always exists a g.l.b. and l.u.b.Let S ⊂ R be a bounded set and let a be the g.l.b of S and b be the l.u.b. of S, then we have: 1. If S is open, then a ∉ S and b ∉ S 2. if S is closed, then a ∈ S and b ∈ SCompact sets : A set is compact if it is closed and bounded.53. Relations and functionsConsider an ordered pair (s, t ) that associated an element s ∈ S to another element t ∈ T . Any collection of such ordered pairs is said to constitute a binary relation between the sets S andT . Note that a binary relation R is a subset of the cross product S × T .Some properties of relations: 1. The relation is complete if either xRy or yRx. 2. 3. 4. transitive if xRy and yRz implies xRz. reflexive if xRx. symmetric if xRy ⇔ yRxExamples: The preference relation ( ≿ ) is complete, transitive and reflexive.The function is a mapping from one set D (domain) to another set R (range) denoted as:f :D→ RThe image of f : I ≡ {y | y = f ( x)} ⊂ R The inverse image of a set of points S ⊂ R is: f −1 (S ) ≡ {x | x ∈ D, f ( x ) ∈ S } The graph of f : G ≡ {(x, y ) | x ∈ D, y = f ( x ) ∈ S } A function is a surjective function if the range ran( f ) = R A function is an injective function (or one to one) if f (a) = f (b) implies a = b A function is bijective if it is both surjective and injective. In a sense, the domain and the range must have the same number of elements.6Homogeneous function A function f ( x1 ,...x N ) is homogeneous of degree r ( for r = ...,−1,0,1,... ) if ∀t > 0 we have:f (tx1 ,...tx N ) = t r f ( x1 ,...x N )Theorem 5 (Euler’s Formula) suppose that f ( x1 ,...x N ) is homogeneous of degree r ( forr = ...,−1,0,1,... ) and differentiable. Then at any (x1 ,..., x N ) we have∑∂f ( x1 ,...x N ) xn = rf ( x1 ,..., x N ) ∂xn n =1NProof: by definition, we have f (tx1 ,...tx N ) − t r f (x1 ,...x N ) = 0 Differentiation this expression with respect to t gives∑∂f (tx1 ,...tx N ) xn − rt r −1 f ( x1 ,..., x N ) = 0 ∂ (txn ) n =1NEvaluating at t = 1 , we obtain Euler’s Formula.□74. ContinuityA function f : R → R is continuous at a point x 0 if ∀ε > 0 , ∃δ > 0 such that d (x, x 0 ) < δ implies that d ( f ( x), f ( x 0 ) ) < ε . Cauchy definition: the function is continuous at the point x 0 ∈ D if ∀ε > 0 , ∃δ > 0 such that f (Bδ ( x 0 ) ∩ D ) ⊂ Bε ( f (x 0 )) A function is continuous function if it is continuous at every point in its domain.Open and closed set in D: A subset S ⊂ D is open in D if for every x ∈ S , there is an ε > 0 such that Bε ( x) ∩ D ⊂ S . A subset is closed in D if its complement S in D, is open in D.Theorem 6The following statements are equivalent: 1.f : D → R n is continuous;2. for every open ball B in R n , f −1 (B ) is open in D; 3. for every open set S in R n , f −1 (S ) is open in D. Remark: the continuous inverse image of an open set is an open set. In short, the inverse mapping of a continuous function can preserve the openness of sets. For what kind of sets the continuous image can preserve its properties? It turns out to be a compact set. The continuous image of a compact set is a compact set.85. Some existence theoremsTheorem 7 (Weierstrass) Existence of Extreme ValuesLet f : S → R be a continuous real-values mapping, where S is a nonempty compact subset of R n . Then there exists two vectors xmax,xmin∈ S such that for all x ∈ S ,f x( ) ≤ f (x ) ≤ f (x )min maxTheorem 8 (Brouwer) Fixed-pointLet S ⊂ R n be a nonempty compact set and f : S → S be a continuous real-values mapping, then there exists at least one fixed point x of f in S . I.e., f ( x ) = x .∗ ∗ ∗96. Real valued functionsSets related to a real valued function f : D → R :L( y 0 ) is a Level set if L( y 0 ) = {x | x ∈ D, f ( x ) = y 0 }, where y 0 ∈ R .Superior and inferior sets: 1. S ( y 0 ) = {x | x ∈ D, f ( x ) ≥ y 0 } is called the superior set (or upper contour set) for levely 0 ∈ R . S ' ( y 0 ) = {x | x ∈ D, f ( x ) > y 0 } is called the strictly superior set for level y 0 ∈ R2. I ( y 0 ) = {x | x ∈ D, f ( x ) ≤ y 0 } is called the inferior set (or lower contour set) for levely 0 ∈ R . I ' ( y 0 ) = {x | x ∈ D, f ( x ) < y 0 } is called the strictly inferior set for level y 0 ∈ RConcave function: ∀x1 , x 2 ∈ D, t ∈ [0,1] , f (tx1 + (1 − t )x 2 ) ≥ tf (x1 ) + (1 − t ) f (x 2 ) Strictly concave function: ∀x1 , x 2 ∈ D, t ∈ (0,1) , f (tx1 + (1 − t )x 2 ) > tf (x1 ) + (1 − t ) f (x 2 ) If the function is differentiable, then it is concave iff f ' ' ( x ) ≤ 0 , and it is strictly concave iff ' ' ( x ) < 0 but the reverse is not true.In the multi-dimensional case, the condition for concavity is equivalent to that the matrix (known as Hessian matrix) of second order derivative is negative semidefinite at every point. If the Hessian matrix of a function is negative definite at every point, then the function must be strictly concave. But the reverse is not true.⎛ ∂ 2 f (x ) ∂ 2 f (x ) ⎞ ⎜ ⎟ ... ⎜ ∂x1∂x1 ∂x1∂xn ⎟ ⎟ D 2 f (x ) = ⎜ ..... ⎜ ⎟ ⎜ ∂ 2 f (x ) ∂ 2 f (x ) ⎟ ... ⎜ ⎟ ⎝ ∂xn ∂x1 ∂xn ∂xn ⎠1011 Convex function: []1,0,,21∈∈∀t D x x , ()()()()()212111x f t x tf x t tx f −+≤−+ Strictly convex function: ()1,0,,21∈∈∀t D x x , ()()()()()212111x f t x tf x t tx f −+<−+ If the function is differentiable, then it is concave iff ()0''≥x f , and it is strictly concave if ()0''>x f but the reverse is not true.In the multi-dimensional case, the condition for concavity is equivalent to that the matrix (known as Hessian matrix) of second order derivative is positive semidefinite at every point. If the Hessian matrix of a function is positive definite at every point, then the function must be strictly concave. But the reverse is not true.()x f is a (strictly) concave iff ()x f − is (strictly) convex.The following statements are equivalent:1. R D f →: is Quasiconcave Function2. []1,0,,21∈∈∀t D x x , ()()()()[]2121,min 1x f x f x t tx f ≥−+3. ()x f − is quasiconvex4. ()y S is convex set for all R y ∈ Quasiconvex Function ?• A function R A f →: is quasiconcave if its upper contour sets (){}t x f A x ≥∈: are convex sets; i.e., if ()t x f ≥ and ()t x f ≥′, then ()()t x x f ≥′−+αα1 for any R t ∈, A x x ∈′, and []1,0∈α.• A function R A f →: is strictly quasiconcave if ()()t x x f >′−+αα1 for x x ′≠ and()1,0∈α.。
微观经济理论I上海财经大学经济学院1微观经济理论•参考书:–G. A. Jehle & P. Reny•Advanced Microeconomic Theory,–A. Mas-Colell, M. D. Whinston & J. R. Green •Microeconomic TheoryA. Rubinstein–A Rubinstein•Microeconomics Lecture noteVarian H R Microeconomic Analysis–Varian, H. R., Microeconomic Analysis2第一讲第讲偏好与选择31. 偏好与选择问题界定:选择函数(choice function)•(choice function)•偏好关系(preference relation)•显示偏好弱公理(weak Axiom of revealed preference)•理性选择与WA:选择函数的可合理化定理选择函数的可合理化定理41.1 选择函数择项•选择项:x–根据问题分析需要,设定个体可以选择的变量•比如–例1:利率或税收政策对消费会产生怎样的影响?•选项:x=(c1, c2)–例2:要素投入决策•选项:x=(k, l)–例3:地方政府基础设施投资激励•选项:x=(I i,C i )51.1 选择函数•选择项:x•选择集:X给定经济环境下,个体可以–想象自己可能选择的各种选择项的集合。
–根据经济环境设定每个变量可能的取值范围•例:•消费者选择集:={(0X {(c 1, c 2):c 1 0, c 2 0}•生产者选择集:X ={(k , l ):k 0, l 0}X 0•地方政府选择集:={(I i , C i ):I i 0, C i 0}61.1 选择函数•选择项:x•选择集:X•可行集:A X⊂–决策者可以选择的选项的集合–反映各种约束对选择的影响•例, c2):(1+r)c1+ c2≤(1+r)y1+ y2}消费者可行集{((1+)+(1+)+–消费者可行集:B={(c1–生产者可行集:B={(x1, x2):y≤f(k, l) }, C i):I i +C i ≤S+tF i }地方政府的可行集{(–地方政府的可行集:B={(Ii71.1 选择函数择项•选择项:x•选择集:X•可行集:A⊂X•D:可能的可行集的集合(X部分子集的集合)–例:–消费者可行集:B(r, y1,y2)–生产者可行集:B(ρ)–地方政府可行集: B(t, F,S)81.1 选择函数•例:大学的选择–可以申请的所有学校:X={x1,x2,..,x N}–A:接受申请的所有学校,可以从中选择一所接受申请的所有学校可以从中选择所–D:2N -1 种可能的选择情形(不考虑∅)•如果学校根据排名,从高到低进行了排序,而且排名高的学校录取了该学生,排名较低的学校都会录取。