当前位置：文档之家 › 第2篇共轴球面系统

第2篇共轴球面系统

  • 格式：ppt
  • 大小：2.85 MB
  • 文档页数：39

下载文档原格式

  / 39

合集下载

第二章球面与共轴球面系统（ＰＤＦ）

第二章球面与共轴球面系统（ＰＤＦ）

第二章球面与共轴球面系统§2－1 光线光路计算与共轴光学系统共轴球面系统—光学系统一般由球面和平面组成，各球面球心在一条直线（光轴）上。

物象关系的研究方法—光线的光路计算。

逐面计算物象的大小、虚实、正倒、位置等特性。

子午面—包含物面与光轴的截面。

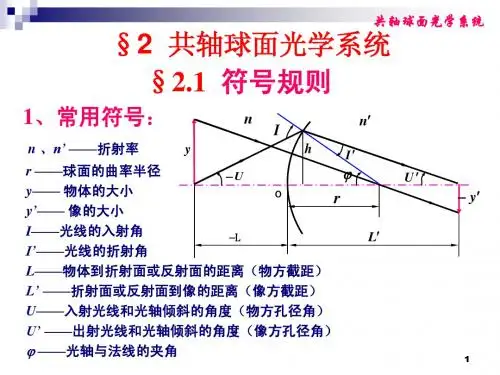
一、 光线经过单个折射面的折射OEAA ′II ′Cr-LL ′hnn ′-UU ′φ1.基本参量E －折射点 OE OE －折射球面 U U 、U ′－ 物象方孔径角O －顶点 h h －入射高度 n n 、n ′－物象方空间折射率C－球心 r－球面曲率半径 I 、I ′－入、折射角A 、A ′－物点、象点 L 、L ′－物距、象距φ －法线与光轴夹角2. 符号法则（便于统一计算）规定光线从左向右传播a）沿轴线段L、L′、r以O为原点，与光线传播方向相同，为“＋”与光线传播方向相反，为“－”b）垂轴线段h在光轴之上，为“＋”在光轴之下，为“－”c）光线与光轴夹角U、U′以光轴转向光线成的锐角来度量，顺时针为“＋”逆时针为“－”d）光线与法线夹角I、I′以光线转向法线成的锐角来度量，顺时针为“＋”逆时针为“－”e）光轴与法线的夹角φ以光轴转向法线成的锐角来度量，顺时针为“＋”逆时针为“－”f）折射面的间隔d，一般取“＋”g）所有参量是含符号的量，但图示标为参量的大小。

二、 远轴光的计算公式（实际光线光路计算） 给定n 、 n ′、r ，已知L 、U ，求解L ′、 U ′ 其中U 、 U ′较大，远轴光线成像（大光路）U I rr L I I U U In nI Ur r L I ′′+=′′−+=′′=′−=sin sin sin sin sin sin OEAA ′II ′Cr-LL ′hnn ′-UU ′φ3）物点位于物方无限远时，入射光线位置由高度h 决定。

rh I =sin 说明：1）L ′＝f (U 、L 、n 、n ′、r)2）当L 为定值时，L ′随U 变化而变化，象方光束失去同心性，成不完善象，形成球差。

第二章 共轴球面系统(1)

第二章 共轴球面系统(1)

符号规则的应用举例：
20º 20º
20º 20º
100
100
符号规则的应用举例：
光路图中所有几何量一律以绝对值标注，负号则
表示该几何量的方位。 应用一定形式的公式可进行各种光路的正确计算。 推导公式时，也要使用符号规则，以便使导出的 公式具有普遍性。
举例：
透镜的结构参数： r1 = 10
d=5
n1 = 1.0 n1’ = n2 = 1.5163 (K9)
r2 = -50
n2’ = 1.0
§ 2-3
近轴成像
当U很小时，U’ ，I与I’ 也相应很小，则这 些角度的正弦值可近似地用弧度值来代替， 并改用小写字母 u，u’ ，i，i’ 来表示。此时， 其他各量均用相应小写字母来表示。 此时，由于u角很小，光线很靠近光轴， 这样的光线称为近轴光线（或称傍轴光线）。 近轴光线所在的区域，称为近轴区（或称傍 轴区）(Paraxial region)。
〈讨论〉
③ 当一物点位于反射镜的球心时，此时 I= -I″= 0 ，即说明从球心发出的 光线被球面镜反射后，反射光线按原 路返回；也就是说，从C点发出的任 何光线经球面镜反射后，仍会聚于C点。
何谓理想光学系统？
此即是把近轴区成完善像的范围扩 大到整个光学系统的任意空间；亦即当 任意大范围的物体以任意宽的光束经光 学系统后均能成完善像的光学系统。
A
-u
C
A’ B’
- u’
O
-l’ -l
球面反射镜的成像特性
1、焦距公式：
f ′= f = r / 2 2、物像关系：
（2-18）
1 / l′+ 1 / l = 2 / r
β=-l’/l α= - β 2 γ= -1 / β

+第2章球面和共轴系统

+第2章球面和共轴系统
说明：1）β>0，y与y’同号，成正像，反之倒像。
2）β>0，l与l’同号，物像虚实相反，反之相同。
3）|β|>1,放大像，反之为缩小像。
利用公式就可以由任意位置和大小的物体，求得单个折射球面所成的近轴像的大小和位置。
2.2
推导：如图所示，ΔABC～ΔA’B’C 。则 -y/y’=(l’-r)/(-l+r)
该式说明：在近轴区域内，l’是l的函数，与u无关，这 表明轴上物点在近轴区域内成完善像。这个像点称为高 斯像点。
2.1
• 使用变换公式的优缺点：
• （1）方便
• （2）在一定条件下是方便的，实际当中有的光 线的孔径角U比较小，至少中心部分是如此。 • （3）将用上式算出 l ' 作为像点位置作为标准位 置，称为高斯像点，设法使 U 角的光线与光轴
k n 2 ' 2 n3 ' 2 2 3 n2 n3
2.3 3.球面反射镜成像
凹面镜成像
凸面镜成像
2.3
1）球面反射镜的物像 位置关系 由 n' n n' n l' l r 当 n' n, 1 1 2 l' l r 2）成像倍率
2.1 2.实际光线经过单个折射球面的光路计算公式
已知：折射球面曲率半径r，介质折射率n和n’， 物方坐标L和U。 求：像方坐标L’和U’。
三角形AEC中应用正弦定律，得到
0 sin( 180 I) sin( U ) L r r
则
sin U sin I (Lr) r
根据折射定律
2.3 2.共轭球面系统的倍率计算
1）.垂轴倍率β
y 2 y y k k 1 y y y y 1 1 y 3 k

《应用光学》共轴球面系统的物像关系 ppt课件

《应用光学》共轴球面系统的物像关系 ppt课件

B
B′
l=0
F′ H A
A′ H′
F
像平面为: 像方主平面
ppt课件 17
2.5 作图法对位于空气中的负透镜组(f′＜０)分别求不 同物距的像平面位置.
B′
f' l 2
B H H′
Aபைடு நூலகம்
F A′
F′
像平面为 A’B’所在平 面,如图示.
ppt课件 18
2.5 作图法对位于空气中的负透镜组(f′＜０)分别求不 同物距的像平面位置.
l = −f′
B
… …
F A
F′ H H′
像平面在像 空间无限远 处.
l′=∞
ppt课件 6
2.4 作图法对位于空气中的正透镜组(f′＞０)分别求不 同物距的像平面位置.
B′ B A′ F A H F′ H′
f' l 2
像平面为 A’B’所在平 面,如图示.
l ′ = −f′
ppt课件 7
2.4 作图法对位于空气中的正透镜组(f′＞０)分别求不 同物距的像平面位置.
B
B′
l=0
F H A
A′ H′
F′
像平面为:
像方主平面
ppt课件 8
2.4 作图法对位于空气中的正透镜组(f′＞０)分别求不 同物距的像平面位置.
B B′ F H A′ H′ A F′
f' l 2
像平面为 A’B’所在平 面,如图示.
l ′ = f′/3
ppt课件 9
2.4 作图法对位于空气中的正透镜组(f′＞０)分别求不 同物距的像平面位置.
ppt课件 13
2.5 作图法对位于空气中的负透镜组(f′＜０)分别求不 同物距的像平面位置.

第二章 共轴球面系统(二)

第二章 共轴球面系统(二)
= l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
共轴球面系统的过渡公式（3-2）
lu l'u' h
l1u1 l'1 u'1 h1 ,l2u2 l'2 u'2 h2 ,
l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
拉格朗日- 赫姆霍兹恒等式
y' nl'
y n'l
lu l'u'
J为拉赫不变量 nuy n'u' y' J
题 例 1：在一直径为30cm的球形玻璃鱼缸内盛满水，鱼缸中
心处有一条小鱼，求缸外观察者看到鱼的位置及放大率！
解： n n n n l' l r
n' 4 ,l 15, r 15代入 3
定义：通过一定光学系统所成的像对光轴的 垂直高度与物本身对光轴的垂直高度的比。
公式：
y'
y
近轴区的放大率
-u
u’
近轴区的放大率----横向放大率
y'
y
y' l'r y l r
n(1 1) n'(1 1)
rl
r l'
物像位置关系式
n l r n' l' r
rl
rl'
l r l' r n' l nl'
n'k 2

应用光学第二章共轴球面系统的物像关系

应用光学第二章共轴球面系统的物像关系

l ' f (n, n ', l , r )
第4节 近轴光学的基本公式 和他的实际意义
• 物像位置关系式
• 推导出 l ' f (n, n ', l , r )
h n ' u ' nu (n ' n) r
L1’
I1 I1’ L1’ U1’
35.96893
11.06815 7.27365 35.96893 2.79450
34.5908
22.57512 14.66568 34.5908 5.90945
32.22743
35.14835 22.31332 32.22743 9.83503
第3节 球面近轴范围内的成像性质 和近轴光路计算公式
• 折射光线位置：
– L’：折射光线与光轴的交点A’到球面顶点的距离。 – U’：折射光线与光轴的夹角。
• 其他已知量：
–球面半径r； –折射球面前后的折射率n、n’。
O
P
n n’ I r L’ L I’
φ
U C’
A’
U
A
第1节 共轴球面系统中的光路计算公式
• 共轴球面系统的光路计算公式
• 已知：L、U、r、n、n’；求L’、U’。 • 对△APC应用正弦定理得到：
第3节 球面近轴范围内的成像性质 和近轴光路计算公式
起始角度U1 L1 r1 -1° -100 10 -2° -100 10 -3° -100 10
(L1-r1)/r1 sinU1
sinI1 I1
-11 -0.017452
0.19198 11.06815
-11 -0.034899
0.38389 22.57512

第2章 共轴球面系统

第2章 共轴球面系统

2.2 单个折射球面的成像放 大率及拉赫不变量
如果在轴上点A附近从球面上取一小块面积 ds并 把它的细光束像记为ds′ ，当面积足够小时，可 近似认为物和像均为在两球面的切平面上。 结论： 结论：当物体以细光束成像时，只有位于近轴 只有位于近轴 区的物体才能成完善像。 区的物体才能成完善像。 二、单个折射球面成像的放大率及拉赫不变量
y′ nl′ β= = y n′l
lu = l ′u ′ = h
nyu = n′y ′u ′ = J
——拉格朗日赫姆霍兹定理，J为拉赫不变量 拉赫不变量 结论：实际光学系统在近轴区内成像时，对于一 对共轭平面来说，物高、物方孔径角和物方介质 折射率的乘积是一个常数。 阿贝不变量： 1 1 阿贝不变量 1 1
2.2单个折射球面的成像放大率 2.2单个折射球面的成像放大率 及拉赫不变量
主要内容： 垂轴平面物体以细光束经折射球面成像 单个折射球面的近轴光线成像放大率 三种放大率的关系 拉赫不变量
2.2单个折射球面的成像放大率 2.2单个折射球面的成像放大率 及拉赫不变量
一、垂轴平面物体以细光束成像
A’是A的完善像点 是 的完善像点，根据物像之间等光程性，可 知 ∑′ 面是 ∑ 面的细光束像。 根据物像位置关系公式知，B点的像在 ∑′ 面左侧 面左侧. B 结论： 结论：如果物是垂轴平面物体，则它经过单个 折射球面折射后，它的细光束像不再是平面， 而是一个比 ∑′ 面更弯曲的曲面，成像不完善 成像不完善— 成像不完善 —像面弯曲 像面弯曲。 像面弯曲
结论：位于近轴区的轴外物点，利用近轴光线 成像时，符合点对点的理想成像关系。
2.1光线经单个折射球面的折射 2.1光线经单个折射球面的折射
4.物像位置关系公式（ 4.物像位置关系公式（l ′与l ) 物像位置关系公式

工程光学第2章 共轴球面光学系统

工程光学第2章 共轴球面光学系统
12
共轴球面光学系统
2. 成像放大率 单折射球面
y′ nl′ = β = y n ′l
dl′ nl′2 n′ α = β = = 2 dl n ′l n
u′ l n 1 γ = = = u l′ n' β
2
共轴球面系统
y'k y'1 y'2 y'k = β 1β 2 β k = β= y1 y1 y 2 y k
U′
y′
L′
1
共轴球面光学系统
2、符号规则 、
（一）光线行进方向：从左向右。 光线行进方向：从左向右。 线量符号： （二）线量符号： (1)沿轴线段：以球面顶点 为原点，与光线行进方向相 沿轴线段： 为原点， 沿轴线段 以球面顶点O为原点 同者为正，与光线行进方向相反者为负。 同者为正，与光线行进方向相反者为负。 (2)垂轴线段：以光轴为界，在光轴之上为正，在光轴之 垂轴线段 以光轴为界，在光轴之上为正， 垂轴线 下为负。 下为负。 角度符号（一律以锐角来衡量）： (三）角度符号（一律以锐角来衡量）： 光线与光轴的夹角 光轴转向光线，顺时针为正， 的夹角： (1) 光线与光轴的夹角：光轴转向光线，顺时针为正，逆 时针为负。 时针为负。 光线与法线的夹角 光线转向法线，顺时针为正， 的夹角： (2) 光线与法线的夹角：光线转向法线，顺时针为正，逆 时针为负。 时针为负。 光轴与法线的夹角 光轴转向法线，顺时针为正， 的夹角： (3) 光轴与法线的夹角：光轴转向法线，顺时针为正，逆 时针为负。 时针为负。
11
1. 过渡公式
共轴球面光学系统
′ ′ ′ n2 = n1 , n3 = n2 , , nk = nk 1 ′ ′ ′ u2 = u1 , u3 = u2 , , uk = uk 1 ′ ′ ′ y 2 = y1 , y 3 = y 2 , , y k = y k 1

第二章球面和共轴球面系统分析

第二章球面和共轴球面系统分析
要讨论成像规律，即像的虚实，成像的位置、正倒和大 小问题，必须计算出光线的走向，所以我们先讨论计算公式。 光线经过单个折射球面的情况如图所示。 包含光轴和物点的平面称为含轴面（纸面）或子午面。 计算的目的：光从何处来，经何处到哪里去（由此得出由物 点发出的光线经过系统后能否交到一点完善成像）？
首要问题：用什么量（怎样）来决定光线在空间中的位置？
对AEC应用正弦定理得 L r r Lr 即 sin I sin U 可求出I sin I sin （ U） r n 据折射定律 sin I ` sin I 可求出I ` n` 对AEC和A`EC应用外角定理 U I U ` I ` U ` U I I ` 可得到U ` sin I ' sin U ' sin I 在A ' EC中 ，利用正弦定律 L ' rr L ' r r sin U
从光轴起算，光轴转向光线（按锐角方向）， 顺时针为正，逆时针为负。
入射角、折射角 从光线起算，光线转向法线（按锐角方向）， 顺时针为正，逆时针为负。 ③ 光轴与法线的夹角（如） 从光轴起算，光轴转向法线（按锐角方向）， 顺时针为正，逆时针为负。
二、实际光线经过单个折射球面的光路计算
已知：折射球面曲率半径r，介质折射率n和n′，及物方坐标L和U。 求：像方L ′和 U ′。
共轴球面系统由许多单个球面构成，当计算出第一面后， 其折射光线就是第二面的入射光线。
U 2 U1; L2 L1 d1
再由相邻两折射球面间的关系，求出下一个球面的折 射光线。
第四节 球面反射镜成像
n n n n 成像公式： l l r

n n
1 1 2 l l r

第二章_共轴球面系统的物像关系

第二章_共轴球面系统的物像关系

1度
2度
3度
起 始 角 度 U2 L2 -r2 L2-r2 ÷r2 ×sinU2 SinI2 ×n2/n’2 SinI’2 ×r2 ÷sinu’2 L’2-r2 +r2 L’2
-1 度
2度 第二面 29.59107 50 79.59107 -50 0.102956 -0.16389 1.5163/1 -0.24850 -50 0.18851 65.9121 -50 15.9121
第二章
共轴球面系统的物像关系
本章内容：共轴球面系统求像。 由物的位置和大小求像的位置和大小
§ 2-1 共轴球面系统中的光路计算公式
求一物点的像，即求所有出射光线位置，交点就是 该物点的像点。
因为所有出射光线位置的求法是相同的，只须找出 求一条出射光线的方法即可。 因为所有的球面的特性是一样的，只须导出光线经过 一个球面折射时,由入射光线位置计算出射光线位置的 公式, 即球面折射的光路计算公式。
例题2
一物体位于凹球面反射镜顶点前40mm，球面反射镜半径为 120mm，求像的位置及轴向放大率。
120mm
近轴光路计算公式总结
u1 , l1 解法一
lr i u r n ' i 'i n u' u i i' ri l r ' uຫໍສະໝຸດ ' 'k个球面
u1 h1 l1
……
hk
lk
d—由前一面顶点算起到下一面顶点。
2．角度： 一律以锐角度量，顺时针转为正，逆时针转为负。 角度也要规定起始轴： U、U'—由光轴起转到光线； I、I'—由光线起转到法线； ψ—由光轴起转到法线，
应用时，先确定参数的正负号，代入公式计算。 算出的结果亦应按照数值的正负来确定光线的相对位置。 推导公式时，也要使用符号规则。

工程光学 章节2 球面系统

工程光学 章节2 球面系统
3. 光路计算是根据给定的光学系统，由物求像或由像 求物的过程。 4. 光路计算是根据几何光学的基本定律利用成像光路 图建立起的物象计算式。
光线经球面折射时的光路计算
要讨论成像规律，即像的虚实，成像的位置、正倒和大小问题，必须 计算出光线的走向，所以我们先讨论计算公式。 包含光轴和物点的平面称为含轴面（纸面）或子午面。
第一种情况
求光束经过两次成像后的会聚，图 已知系统 r1 R r2 R n1 1 n2 1.5 n3 1
•第一次成像
n1 1
n'1 1.5
r R
l1
1.5 1 1 .5 1 l '1 R
l1 '求得
A′ -Y′ B′
规则： 以球面的顶点为原点 2-1 沿轴量向右取正，向左取负 垂轴量向上取正，向下取负
单个球面的折射光路
B Y
A -U -L n E I
h I′ O C U′ r L′
n′
A′ -Y′ B′
2-1
角度的符号
• 角度量：U、U′、I、 I ′、φ
规则： 角度正切值为正时该角度为正，反 之为负
第二章 共轴球面光学系统
第一节 光路计算
• • • • 一、概述 二、符号规则 三、单个球面的成像计算 四、共轴球面的成像计算
一、概述
1. 绝大多数光学系统由球面、平面或非球面组成，如 果各曲面的曲率中心在一条直线上，则称该光学系 统为共轴光学系统，该直线为光轴。
2. 非球面, 如抛物面、椭球面等对某些位置等光程的 像质不错, 但加工检验有一定困难。因此，后面的讨 论主要是由球面和平面组成的光学系统。
• 实际光线的光路计算
严格按照几何光学基本定律的光线计算，这类 光线称为实际光线

应光第二章 球面系统 答案

应光第二章 球面系统 答案

第二章球面和共轴球面系统2.1某一透镜结构参数如下：r/mm d/mm n100300 1.5∞当l=-∞时，求l'，在第二个面（平面）上刻十字线，试问通过球面的共轭像在何处？当入射高度h=10mm时，实际光线和光轴的交点应在何处？在高斯面上的交点高度是多少？这个值说明了什么问题？解：l'=0，在第二面上十字线其共轭像在无限远。

H=10mm，实际光线与广州交点l'=299.33203mm，这说明了该光线经球面折射后不交于锦州光像点，所以一个物点得到的1像是一个弥散斑。

2.2一个玻璃球的直径为400mm，玻璃折射率n=1.5，球中有两个小气泡，一个正在球心，另一个在1/2半径处，沿两气泡的连线方向在球的两边观察两个气泡，它们应在什么位置？如果在水中（n=1.33）观察。

则它们应在什么位置？解：设一个气泡在中心处，另一个在第二面和中心之间。

（1）从右侧观察时，如图a：a b（2）从左侧观察时如图b：（3）在水中时： 中心气泡所成像： ，n '=1.33 n=1.5，r=200mm ，l=200mm 得到：l'=200mm 仍在圆心处1/2半径处气泡所成像：，n '=1.33 ，n=1.5，r=200mm ，l=100mm 时 ， l'=94mml=-300mm 时 ， l'=-320mm2.3一个玻璃球直径为60mm ，玻璃折射率n=1.5，一束平行光射在玻璃球上，其会聚点应在什么位置？解：首先考虑光束射入玻璃球第一面时的状态，使用高斯公式：由 1n '=1.5 1r =30mm 1n =1 1l =∞得到：1l '=90mm对于第二面，d=60mm ，2l =1l '-d=30mm由 22'222'22'r n n l n l n -=- 2n =1.5 2n '=1 2r =-30mm 1n =1 2l =30mm 得到：2l '=15mm会聚点位于第二面后15mm 处。

应用光第二章 共轴球面系统的物像关系

应用光第二章 共轴球面系统的物像关系
2
➢符号规则
• 光线的传播方向：自左向右为正 • 线段
• 沿轴:以球面顶点o为起点，自左向右为正，－L，r，L′ • 垂轴 h，光轴为起点，向上为正，向下为负。 • 球面的曲率半径：球心在球面顶点的右方为正，反之为负
• 角度(一律以锐角来度量，顺时针转为正，反之为负；正切方法）
• 光线与光轴的夹角：光轴转向光线 -U，U′ • 光线与法线的夹角：光线转向法线 I，I′
近轴条件有
h lu lu
8
光焦度
物理意义
n' n r
>0 会聚 ＝0 平面折射 <0 发散
l l'
l'
f
'
n,
n' /(
n)
n,
/
r
l f -n /(n' n) -n / r
f ' n' fn
n n n n l l r
n, / f ' -n / f
第二章 共轴球面系统的物像关系 Coaxial Spherical System
1
➢基本概念
•光轴：若光学系统由球面组成，它们的球心位于同一直线上，
则称为共轴球面系统，这条直线为该光学系统的光轴。实际 上，光学系统的光轴是系统的对称轴
•子午面：通过物点和光轴的截面 • 物方截距 •像方截距 •物方孔径角 •像方孔径角
1) r2
(n 1)2 d nr1r2
1 f
4. 计算主平面位置。
lH
n(r2
r1d r1) (n 1)d
lH'
n(r2
r2d r1) (n 1)d
63
5. 两个主平面之间的距离。

第二章共轴球面系统

第二章共轴球面系统
dx' x' α= = dx x
讨论: ① α恒为正,当物点沿轴向移动时,像点沿轴同 向移动 ②一般α≠ β,即空间物体成像后要变形,如正方 体. ③只有在dl 很小时才适用
3. 角放大率
共轭光线与光轴夹角u ′和u 的比值,称为角放大率.
B' K B K'
H
A F
H'
F'
A'
对共轴理想光学系统性质第三点的解释: 一个共轴理想光学系统,如果已知两对共轭面的位置和放 大率,或者一对共轭面的位置和放大率,以及轴上两对共 轭点的位置,则其他一切物点的像点都可以根据这些已知 的共轭面和点确定
§2.8 理想光学系统的物像关系式
I I' B'
2.近轴光路计算公式 在近轴几何光学中,经常用到以下近似公式(一 级泰勒展开)
sin U ≈ U ≈ tan U
1 1 (sin θ = θ θ 3 + θ 5 ......) 3! 5!
U为物方孔径角,是个很小值(<<1rad),当 U<5°,近似代替误差大约为1%.
代入到(2-1)-(2-3),并用小写字母表示,得到以下公式:
dl ′ α = dl
(1)高斯公式求解:
f' f + =1 l' l
f ' dl ' fdl '2 2 = 0 l l
fl ' α = 2 f 'l
dl ′ nl ′2 n′ 2 = 2 = β α= dl n′l n
2
(2)牛顿公式求解:
xx' = ff '
xdx'+ x' dx = 0

第二章 球面和共轴球面系统

第二章 球面和共轴球面系统
2）物体移动有限距离
此时轴向倍率可以表示为：
α＝
l2 '− l1 ' l2 − l1
高斯公式
β1为第一位置处的垂轴放大率；β2为第二位置处的垂轴放大率。
2.2.3 角倍率γ
角放大率γ ：近轴区内，一对共轭光线的像方孔径 角u与物方孔径角u’之比， 即：
2.2.4
三个倍率之间的关系
即轴向放大率与角放大率之积与垂轴放大率相等。 即轴向放大率与角放大率之积与垂轴放大率相等。
2.2.1 垂轴倍率β 2.2.2 轴向倍率α 2.2.3 角倍率γ 2.2.4 三个倍率之间的关系 2.2.5 拉格朗日-赫姆霍兹不变量
2.2.1 垂轴倍率β
定义：像的大小与物的大小比值。 其数学表示形式为：β=y' /y
近轴区有限大小的物体 经过单个折射球面的成像
从图中可见，根据三角形ABC与A’B’C相似有：
现在对于已知的现在对于已知的ll和和uu值无论值无论uu为何值为何值l表明表明轴上点在近轴区成像轴上点在近轴区成像时其像可认为是时其像可认为是完善完善的称为称为高斯像点高斯像点过高斯像点垂直于光轴的面称为过高斯像点垂直于光轴的面称为高斯像面高斯像面构成物像关系的一对点称为构成物像关系的一对点称为共轭点共轭点
2.4 球面反射镜
前面指出，反射定律可认为是折射定律在n’=-n时的 特例，因此，将之前的折射球面的计算公式代以 n’=-n，可以得到相应的反射球面计算公式。 2.4.1 球面反射镜的物像位置公式 2.4.2 球面反射镜的成像倍率 2.4.3 球面反射镜的拉赫不变量
2.4.1 球面反射镜的物像位置公式
以上三式是我们计算单折射球面物像之间关系的基本公式
2.1.3 近轴光的光路计算公式

基于Zemax的应用光学教程 第2章 共轴球面系统成像理论

基于Zemax的应用光学教程 第2章 共轴球面系统成像理论
光学系统
光学系统
子午面
子午面
光轴
轴外物点
光轴
子午面
轴上物点
任意平面
主光线
➢ 轴上物点包含共轴球面系统的对称轴(光轴） ➢ 轴外物点的主光线与光学系统主轴所
构成的平面为子午面。
的所有截平面都称为子午面。
➢ 轴外物点的子午面有且只有一个
➢ 轴上物点的子午面有任意多个
4
南京大学 Nanjing University
2!
4!
6!
当θ很小即近轴条件下，上述级数中θ²以上各项可以忽略，
即有 ≈， ≈ ， ≈ 。
18
南京大学 Nanjing University
近轴光线
★ 近轴条件：sin i tani i
光线在主轴附近很小的区域，
且与主轴夹角较小（<5度）。
★ 实际光线用大写字母，
19
南京大学 Nanjing University
近轴光线
nrl
l
nl n(l r )
像距只与物距有关与角
度无关能成完善像
★ 近轴细光束所成的完善像。——高斯像
★ 高斯像面通过高斯像点且垂直于光轴的平面。
——高斯像面
★ 物像共轭点
20
南京大学 Nanjing University
近轴光线
何为近轴并没有严格的规定，根据实际应用情况而定。
实际非理想情况表现出来的是像差，需要优化设计
表2-1 不同角度的正弦值与其弧度的相对误差
sin
sin
相对误差
θ/°
sin θ
θ/rad
0.5
0.008727
0.008727

工程光学第二章知识点

工程光学第二章知识点

第二章共轴球面光学系统第一节符号规则●常见的光学系统有多个光学零件组成，每个光学零件往往由多个球面组成●这些球面的球心在一条直线上即为“共轴球面系统”●这条直线称为“光轴”●折射球面的结构参数：曲率半径r、物方折射率n、像方折射率n'●入射光线的参数：物方截距L、物方孔径角U●像方量在相应的物方量字母旁加“ ’ ”区分●光线的传播方向为自左向右●规定符号规则如下：●1）沿轴线段（如L、L’和r）●以顶点为原点，与光线方向相同为正，相反为负●2）垂轴线段（如h、y和y’）●以光轴为基准，光轴以上为正，以下为负●3）光线与光轴的夹角（如U、U’）●光轴转向光线；角量均以锐角计、顺时针为正、逆时针为负●4）光线与法线的夹角（如I、I’、I”）●光线转向法线●5）光轴与法线的夹角（如φ）●光轴转向法线●6）折射面间隔d●前一面顶点到后一面顶点，与光线方向相同为正，相反为负；在折射系统中，d恒为正●物方截距、像方截距、物方孔径角、像方孔径角等物理量是可以有正负的，但作为几何量AO、OA’、∠EAO、∠EA’O等应为正值；在负值物理量前加负号，以保证相应几何量为正●根据物像的位置判断物像的虚实●负（正）物距对应实（虚）物●正（负）像距对应实（虚）像第二节物体经过单个折射球面的成像1，单球面成像的光路计算已知折射球面的结构参数曲率半径r ，物方折射率n ，像方折射率n ’已知入射光线AE 的参数物方截距L ，物方孔径角U （轴上物点）求出射光线参数像方截距L ’，像方孔径角U ’（轴上像点）光路计算2在ΔAEC 中用正弦定律，有 sin sin()I U r L r -=-导出求入射角I 的公式sin sin L r I U r -=（2-1）由折射定律可以求得折射角I ’sin sin n I I n '=='（2-2）由角度关系，可以求得像方孔径角U ’U U I I ''=+-（2-3） 在ΔA ’EC 中应用正弦定律，得像方截距L ’ sin sin I L r r U ''=+' （2-4）式（2-1）至（2-4）就是子午面内实际光线的光路计算公式，利用这组公式可以由已知的L 和U 求L ’和U ’ sin sin L r I U r -= sin sin n I I n '=='U U I I ''=+-sin sin I L r r U ''=+'当物点A 位于轴上无限远处时，相应的L=∞，U=0，则式（2-1）须改变为sin hI r =（2-5）●若L 是定值，L ’是U 的函数，即从同一点发出的光线，孔径角不同，将在像方交在不同的点上 ● 同心光束经过单球面后不再是同心光束●这种误差被称为“球差” ●球差是各种像差中最常见的一种●如果把孔径角U 限制在很小的范围内，光线距光轴很近，称为“近轴光”，U 、U ’、I 和I ’都很小，式（2-1）~（2-4）中的正弦值用弧度来表示 ● 用小写字母u 、u ’、i 、i ’、l 和l ’表示近轴量● l r i u r n ii n u u i i i l r r u -='='''=+-''=+'（2-6）~（2-9） ● 当入射光线平行于光轴时，也以h 作为入射光线的参数，有●h i r =（2-10） ●近轴光线l ’与u 无关，即当物点位置确定后，其像点位置与孔径角u 无关，物点发出的同心光束经折射后在近轴区仍为同心光束 ●在近轴区成的是完善像，这个完善像通常称为“高斯像” ● 近轴区最常用的物像位置公式●n n n n l l r ''--='（2-14） ●已知物点位置l 求像点位置l ’时（或反过来）十分方便 ●1、轴上物点：轴上同一物点发出的近轴光线，经过球面折射以后聚交一点，即轴上物点近轴成像时是符合理想成像条件的。

[小学教育]第2章 共轴球面系统的物像关系

[小学教育]第2章 共轴球面系统的物像关系

5
• 当角度足够小时，上述角度的正弦值与弧度值 几乎没有差别，此时角度U,I,U',I' 的正弦值可 以用相应的弧度值u,i,u',i' 来代替。为了区别， 也用小写字母 表示，见图2.2-1。因为这种光线 很靠近光轴，所以称为近轴光线。
6
对于近轴光线，其光路计算公式可以直接由上 节公式得到，这只要将其中的角度的正弦值用弧 度值来代替即可
n1l1 ' n2l2 ' nk lk ' n1 l1 ' l2 'lk ' n1 ' l1 n2 ' l2 nk ' lk nk ' l1l2 lk n1 u1 u2 uk n1 u1 nk ' u1 ' u2 ' uk ' nk ' uk '
22
15
三、角放大率（倍率）γ 在近轴区以内，通过物点的光线经过折射后，必 然通过相应的像点，这样一对共轴光线与光轴的 夹角 和u的比值即为角放大率γ
u' u
利用关系式 lu=l'u'，可得
（2－17）
l n 1 l ' n' n' 2 n 1 n n'
19
物体A1B1(y1) 经第一面成像后的像A1'B1'(y1') 就 是第二面的物体A2B2(y2) ；第一面物方孔径角u1的 近轴光线折射后的像方孔径角 u1'就是第二面的物方 孔径角u2 ；第一面的像方折射率 n1'就是第二面的 物方折射率n2 。其余类推，就有
y2 y1 ' , y3 y2 ' , , yk y 'k 1 ,
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第 2章 球面和球面系统
主要内容：符号规则；光线经过单个折射球 面的光路计算公式；单个折射球面成像放大 率及拉赫不变量；共轴球面系统的转面公式、 放大率和拉赫公式；球面反射镜的物像位置 关系公式及成像放大率。
重点:符号规则；近轴光线经单个折射球面的 物像关系公式；共轴球面系统的转面公式、 拉赫公式和放大率。
2.1光线经单个折射球面的折射
2.近轴光线的光路计算公式：
sin I L r sinU sin I n sin I
r
n
U U I I L r(1 sin I ) sinU
光线平行于光轴:光线的入射角用光线的入射高度
表示为： i h / r
2.1光线经单个折射球面的折射
3.成像性质：
难点：近轴光线的物像位置关系公式；单个 折射球面的拉赫不变量；共轴球面系统的转 面公式、拉赫公式和放大率。
物体 物点
光学系统
像
规律
像点
入射光线
单个折射 球面
出射光线
2.1光线经单个折射球面的折射
主要内容: 符号规则 光线经单个折射球面的实际光路计算公式 光线经单个折射球面的近轴光路计算公式 近轴物像位置关系公式 单个折射球面的成像放大率
2.1光线经单个折射球面的折射
四、光线经单个折射球面的近轴光路的计 算公式
1. 概念：
近轴光线：与光轴很靠近的光线，角度的正弦 值、正切值可以用角度的弧度值代替.
近轴区：近轴光线所在的区域。其中有关的量 用小写字母表示：u,l,i,i,u,l
近轴区没有明确界限，由允许的相对误差大小 确定.相对误差大小：0.1%——各角度小于5°
3.近轴光线经折射球面计算的其他形式
近轴光线满足：lu lu h
n n n n
(1)
l l r
推导出下面的公式 n(1 1) n(1 1) Q (2)
rl
r l
nu nu n n h
(3)
r
➢ （1）式表示物像位置的关系；（2）式称为阿贝
不变量公式，它表示单个折射球面物方和像方的
U U I I
sin I n sin I n
L r(1 sin I ) sinU
2.1光线经单个折射球面的折射
结论：出射光线的位置坐标L’是入射孔径角U 的函数，不同U的入射光线经球面折射后不交 于一点，成像不完善。
2. 物点位于轴上无限远:它发出的光束是平行于 光轴的平行光束，即 L , ，U 此0 时光线的入射 角可用下式计算： sin I h / r
2.2 单个折射球面的成像放
大率及拉赫不变量
如果在轴上点A附近从球面上取一小块面积ds并 把它的细光束像记为ds， 当面积足够小时，可近 似认为物和像均为在两球面的切平面上。
结论：当物体以细光束成像时，只有位于近轴 区的物体才能成完善像。
二、单个折射球面成像的放大率及拉赫不变量
物体 位置
物像位置 关系公式
2.2单个折射球面的成像放大率 及拉赫不变量
一、垂轴平面物体以细光束成像
A’是A的完善像点，根据物像之间等光程性，可 知 面是 面的细光束像。
根据物像位置关系公式知，B点的像在面左侧. 结论：如果物是垂轴平面物体，则它经过单个
折射球面折射后，它的细光束像不再是平面， 而是一个比 面 更弯曲的曲面，成像不完善—— 像面弯曲。
线，顺正逆负； 光轴与法线组成角度(φ)：光轴以锐角方向转到
法线，顺正逆负。 注：优先性：光轴、光线、法线。
2.1光线经单个折射球面的折射
三、光线经单个折射球面的实际光路计算公式 1.由入射光线求出射光线：已知r，n，n’，L，U,
求L’，U’。
利用正弦定理、折射定律和外角定理可得
sin I L r sinU r
像的 位置
像的大小、正倒、虚实？
1. 垂直放大率：像高与物高之比，或称为横向放
Q值相等；（3）式表示近轴光线经球面折射后
物像方孔径角的关系。
➢ 例题：有一折射球面，其参数为 r 20mm,n 1,n 1.5163, 物距为 l 6，0m求m 像距的值。
2.2单个折射球面的成像放大率 及拉赫不变量
主要内容： 垂轴平面物体以细光束经折射球面成像 单个折射球面的近轴光线成像放大率 三种放大率的关系 拉赫不变量
二、符号规则 1.光线传播方向：规定光线从左向右传播为正。
2.线段： 沿轴线段:以顶点O为基准，左负右正；
垂轴线段:(h)以光轴为准，上正下负；
间隔d：以前一个面为基准，左负右正。
2.1光线经单个折射球面的折射
3.角度： 光轴与光线组成角度：光轴以锐角方向转到光
线，顺时针正逆时针负； 光线与法线组成角度：光线以锐角方向转到法
l
2.1光线经单个折射球面的折射
轴外点近轴光线成像：对于单个折射球面，如 果Ｂ点离主光轴很近，则Ｂ点发出的近轴光线 相对于主光轴来说也是近轴光线，经球面折射 后交于一点。
结论：位于近轴区的轴外物点，利用近轴光线 成像时，符合点对点的理想成像关系。
2.1光线经单个折射球面的折射
ቤተ መጻሕፍቲ ባይዱ
4.物像位置关系公式（ l与)l
2.1光线经单个折射球面的折射
一、概念
1.子午平面：包含光轴的平面。 2.截距：物方截距——物方光线与光轴的交点到顶
点的距离；像方截距——像方光线与光轴的交点 到顶点的距离。 3.孔径角：物方孔径角——物方光线与光轴的夹角； 像方孔径角——像方光线与光轴的夹角。
2.1光线经单个折射球面的折射
分界面有左右，球面有凹凸，光轴有上方下方，如 何区别？
i lru r
i n i n
u u i i
l r r i u
u ir lr
i( 1 1) i( 1 1)
l r
lr
颠倒相除 r
u ir l r
n n n n (1) l l r
像的位置l只与物点的位置 和l 折射球面的结构 及物像方介质折射率有关。
2.1光线经单个折射球面的折射
由近轴光线光路计算公式可知，当角度u扩 大或减小K倍，i, i’ ,u’均扩大或缩小K倍。
ki l r ku r
ku ku ki ki
ki n ki n
l r r ki r r i
ku
u
结论：当入射光线的u改变时，l值不变，即 由同一物点发出的近轴光线，经单个折射球 面折射后交于同一点，成完善像。