下载文档原格式
第二章球面与共轴球面系统§2－1 光线光路计算与共轴光学系统共轴球面系统—光学系统一般由球面和平面组成，各球面球心在一条直线（光轴）上。
物象关系的研究方法—光线的光路计算。
逐面计算物象的大小、虚实、正倒、位置等特性。
子午面—包含物面与光轴的截面。
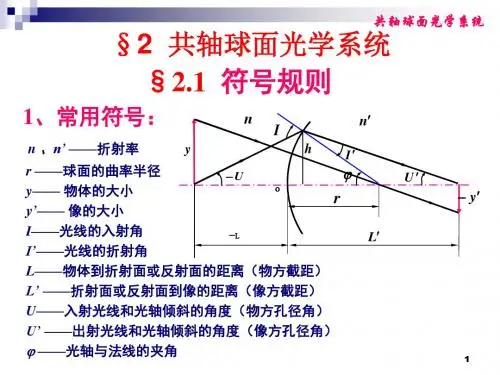
一、 光线经过单个折射面的折射OEAA ′II ′Cr-LL ′hnn ′-UU ′φ1.基本参量E －折射点 OE OE －折射球面 U U 、U ′－ 物象方孔径角O －顶点 h h －入射高度 n n 、n ′－物象方空间折射率C－球心 r－球面曲率半径 I 、I ′－入、折射角A 、A ′－物点、象点 L 、L ′－物距、象距φ －法线与光轴夹角2. 符号法则（便于统一计算）规定光线从左向右传播a）沿轴线段L、L′、r以O为原点，与光线传播方向相同，为“＋”与光线传播方向相反，为“－”b）垂轴线段h在光轴之上，为“＋”在光轴之下，为“－”c）光线与光轴夹角U、U′以光轴转向光线成的锐角来度量，顺时针为“＋”逆时针为“－”d）光线与法线夹角I、I′以光线转向法线成的锐角来度量，顺时针为“＋”逆时针为“－”e）光轴与法线的夹角φ以光轴转向法线成的锐角来度量，顺时针为“＋”逆时针为“－”f）折射面的间隔d，一般取“＋”g）所有参量是含符号的量，但图示标为参量的大小。
二、 远轴光的计算公式（实际光线光路计算） 给定n 、 n ′、r ，已知L 、U ，求解L ′、 U ′ 其中U 、 U ′较大，远轴光线成像（大光路）U I rr L I I U U In nI Ur r L I ′′+=′′−+=′′=′−=sin sin sin sin sin sin OEAA ′II ′Cr-LL ′hnn ′-UU ′φ3）物点位于物方无限远时，入射光线位置由高度h 决定。
rh I =sin 说明：1）L ′＝f (U 、L 、n 、n ′、r)2）当L 为定值时，L ′随U 变化而变化，象方光束失去同心性，成不完善象，形成球差。
第二章共轴球面系统的物像关系本章内容：共轴球面系统求像。
由物的位置和大小求像的位置和大小。
φ U ˊ - UO C A A ˊ n n ˊ P- LrL’II’Q1. 符号规则反射情形看成是折射的一种特殊情形：n’= －n把反射看成是n’= －n 时的折射。
往后推导公式时，只讲折射的公式；对于反射情形，只需将n’用－n代入即可，无需另行推导。
（1） 物像位置关系式rn n l n l n -=-'''2. 近轴光学的基本公式（2） 物像大小关系式这就是物像大小的关系式。
利用公式就可以由任意位置和大小的物体，求得单个折射球面所成的近轴像的大小和位置。
对由若干个透镜组成的共轴球面系统，逐面应用公式就可以求得任意共轴系统所成的近轴像的位置和大小。
l n nl y y '''==β3. 共轴理想光学系统的基点——主平面和焦点近轴光学基本公式的缺点：物面位置改变时，需重新计算，若要求知道整个空间的物像对应关系，势必要计算许多不同的物平面。
已知两对共轭面的位置和放大率，或者一对共轭面的位置和放大率，以及轴上的两对共轭点的位置，则其任意物点的像点就可以根据这些已知的共轭面和共轭点来求得。
光学系统的成像性质可用这些基面和基点求得最常用的是一对共轭面和轴上的两对共轭点。
（1） 放大率β=1的一对共轭面——主平面rn n l n l n -=-'''l n nl y y '''==β不同位置的共轭面对应着不同的放大率。
放大率β=1的一对共轭面称为主平面。
物平面称为物方主平面，像平面称为像方主平面。
两主平面和光轴的交点分别称为物方主点和像方主点，用H 、H’表示，H 和H’显然也是一对共轭点。
主平面性质：任意一条入射光线与物方主平面的交点高度和出射光线与像方主平面的交点高度相同（2）无限远轴上物点和它所对应的像点F’——像方焦点rn n l n l n -=-''' 当轴上物点位于无限远时，它的像点位于F’处。
