高速铁路桥梁结构型式
- 格式:docx
- 大小:20.18 KB
- 文档页数:7


中国铁路桥梁划分标准
中国铁路桥梁的划分标准通常基于以下几个方面:
1. 承载能力:根据桥梁的承载能力,可以将其划分为以下几个等级:
-特大桥:能够承受极高载荷的大型桥梁,如跨越大江、深谷等的桥梁。
-大桥:能够承受较高载荷的中型桥梁,如跨越湖泊、河流等的桥梁。
-中桥:能够承受一般载荷的中小型桥梁,如跨越山谷、平原等的桥梁。
-小桥:承受较小载荷的小型桥梁,如跨越溪流、小河流等的桥梁。
2. 结构形式:根据桥梁的结构形式,可以将其划分为以下几种类型:
-梁桥:由梁体直接承载车辆和行人的桥梁,通常为简单的横梁结构。
-拱桥:由弧形的拱体承载荷载的桥梁,能够有效分散荷载并提供稳定支撑。
-斜拉桥:通过拉索将桥面与桥墩相连接的桥梁,能够在较大跨度上提供承载能力。
-悬索桥:通过主悬索和斜拉索将桥面悬挂在主塔上的桥梁,具有较大的跨度和承载能力。
3. 功能用途:根据桥梁的功能用途,可以将其划分为以下几类:
-高速铁路桥梁:用于承载高速列车的桥梁,需要具备高强度和稳定性。
-普通铁路桥梁:用于承载普通列车的桥梁,通常在载荷和设计上相对较轻。
-支线铁路桥梁:用于承载支线或辅助线列车的桥梁,通常跨度较小,结构相对简单。
-转辙架桥梁:用于支持铁路转辙架的桥梁,需要具备较高的稳定性和可靠性。
这些标准可以根据具体的铁路桥梁设计和建设需求进行调整和细分。
此外,还有一些其他的因素,如地理条件、环境要求等,也会影响铁路桥梁的划分和设计。

德国咼速铁路线上的桥梁结构型式1. 设计速度250 km/h、全长327 km的德国汉诺威一维尔茨堡和全长104 km的曼海姆一斯图加特两条新干线上,共有桥梁359座,总延长37 km。
在359座桥中,152座跨越公路,139座跨越铁路,其余68座为大型山谷桥和高架桥。
2. 从桥梁总长与线路总长之比来看,德国高速铁路上的桥梁数量远小于日本新干线和我国拟建的京沪高速铁路线。
3. 德国这两条新干线上的桥梁几乎全部是预应力混凝土和钢筋混凝土桥。
其原因一方面是混凝土桥养护维修方便、造价也较低,另一更主要的的原因则是混凝土桥在高速行车条件下的噪音远比钢桥低。
4. 在德国的这两条新干线上,大部分桥为预应力混凝土简支梁和连续梁。
5. 简支梁的墩中心距基本上采用44 m及58 m两种,25 m的只有少数几跨。
墩中心距44 m的梁跨度为42 m,58 m的梁跨度55.75 m。
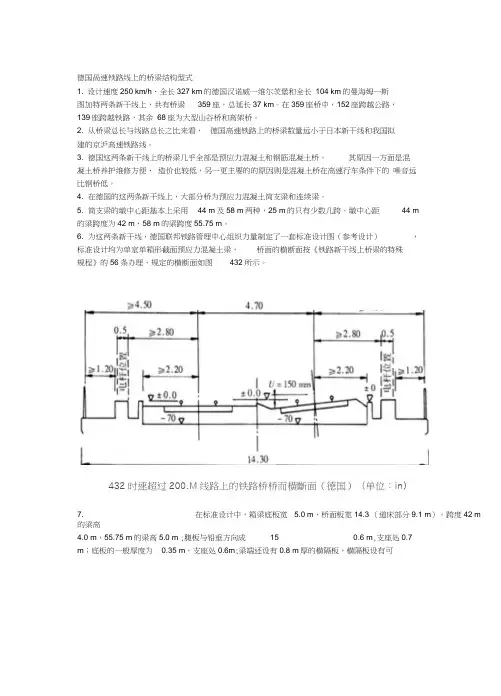
6. 为这两条新干线,德国联邦铁路管理中心组织力量制定了一套标准设计图(参考设计),标准设计均为单室单箱形截面预应力混凝土梁,桥面的横断面按《铁路新干线上桥梁的特殊规程》的56条办理,规定的横断面如图432所示。
432时速超过200.M线路上的铁路桥桥而横斷面(德国)(单位:in)7. 在标准设计中,箱梁底板宽 5.0 m,桥面板宽14.3 (道床部分9.1 m)。
跨度42 m 的梁高4.0 m,55.75 m的梁高5.0 m ;腹板与铅垂方向成15 0.6 m,支座处0.7m;底板的一般厚度为0.35 m,支座处0.6m;梁端还设有0.8 m厚的横隔板,横隔板设有可供维修人员及小车通行的洞。
迪陽舟it山圾桥(6)祭转勒Jt斯爭塔尔山谷桥图433痔国高速铁路桥梁的上部结构典型橫截面图(单位:cm)確国高速铁路桥彖时典型善敷表43.5法国高速铁路线上的高架桥1•运行TGV列车的法国大西洋高速铁路时速为300 km/h,总长263 km。
总共修建了10座双线高架桥,总长 3 523 m,单线高架桥3座,总长455 m,其数量相对说来非常少,这些高架桥的基本资料列于表436中蛙国夭西漁宫速鉄路肓架桥^U6从表436所反映的情况可见,绝大部分桥都采用预应力混凝土箱梁。




桥梁拱形结构当我们行驶在高速公路上或者穿过一道铁路桥时,或许很少有人会想过这些巨大的桥梁是如何支撑起整个结构的。
事实上,这些桥梁的背后隐藏着一种古老而优雅的建筑结构:拱形结构。
本文将以桥梁拱形结构为题,介绍拱形结构的原理、优势以及一些拱形结构桥梁的实例。
一、拱形结构的原理拱形结构是一种弯曲而稳固的结构形式,它将受力均匀地分布到支撑点上。
以桥梁为例,拱形结构通过桥墩和拱体之间的力传递来承受桥梁上的荷载。
当车辆通过桥梁时,重力会传递到桥墩,而桥墩会把这些力传递到拱体上,使得整个结构获得均衡和稳定。
拱形结构的原理可以用弧线上的压缩力来解释。
根据物理学原理,任何物体都会在受力作用下产生力的反作用。
在拱形结构中,当桥梁上的荷载通过拱体传入桥墩时,拱体会向下产生一个向内的压缩力,而桥墩则会产生一个向外的压力以抵消这个向内的压缩力。
这种力的平衡使得拱形结构能够承受更大的荷载,并且具有极高的稳定性。
二、拱形结构的优势1. 强大的承重能力:拱形结构通过合理的分布受力,能够更好地承受荷载。
相比于其他结构形式,拱形结构能够将荷载均匀地分散到桥梁或建筑物的基础上,从而减小了单点的压力,提高了整体的承重能力。
2. 灵活性和适应性:拱形结构可以适应不同的地理环境和地质条件。
在不同的地区和地形条件下,拱形结构可以根据实际情况进行调整,以确保结构的稳定性和安全性。
3. 经济性:由于拱形结构能够提供较大的承重能力,所以可以节省建筑材料的使用。
相对于其他结构形式,拱形结构所需的材料更少,从而减少了成本和建设时间。
三、拱形结构桥梁的实例1. 渡阳高架桥:位于中国广东省深圳市,该桥横跨深圳河。
渡阳高架桥采用了拱形结构,拱体呈现出优美的曲线,不仅提供了高强度和稳定性,而且也成为了城市地标。
2. 伊苏祖高架桥:位于法国巴黎西北部,该桥是一座拱形结构的公路桥梁,横跨塞纳河。
伊苏祖高架桥以其典雅的设计和高承重能力而闻名,成为了巴黎的重要交通枢纽之一。



高速铁路桥梁桥式方案的确定思路随着高速铁路的发展,高速铁路桥梁也成为了重要的工程之一。
在高速铁路桥梁建设过程中,桥式方案的确定是至关重要的一步。
本文将介绍高速铁路桥梁桥式方案的确定思路。
一、确定桥梁类型在确定高速铁路桥式方案之前,需要先确定桥梁的类型。
常见的高速铁路桥梁类型有梁式桥、拱桥、斜拉桥和悬索桥等。
根据设计要求和现场条件,选择最适合的桥梁类型。
二、确定荷载和桥跨在确认桥梁类型后,需要确定荷载和桥跨。
荷载是指在运行过程中对桥梁所施加的力,包括垂直荷载和横向荷载。
桥跨是指横跨于两侧支承墩或两侧基础的距离。
根据荷载和桥跨确定桥梁主梁的型号和横截面尺寸。
三、确定地质条件和环境要求确定桥式方案前,需要对桥梁所在的地质条件和环境要求做好充分的了解。
包括地震性质、风荷载、温差和构筑物周边环境等因素,这些因素将影响桥梁的设计和建造。
四、确认桥墩和基础在确定桥梁类型、荷载、桥跨和地质条件等因素后,需要确定桥墩和基础的类型和配置方案。
桥墩和基础是桥梁的支撑结构,与桥梁的运行、安全及维修密切相关。
根据荷载、地质条件、环境要求确定桥墩和基础的位置、高度、尺寸和材质。
五、确定桥式方案在前四步的准备工作完成之后,可根据已确认的数据,综合考虑桥梁的建设成本、施工难度、建筑工期、安全要求等因素,最终确定桥式方案。
确保桥式方案的结构合理、稳固可靠、经济合理、机械化程度高、利于施工和维修。
六、优化桥式方案绘制桥梁的结构草图及参数表,并模拟验证桥梁的破坏模式、安全极限状态、变形和振动情况等,根据结果对桥式方案进行优化。
优化后的桥式方案能够满足性能、安全和节能等多重要求。
七、完成详细设计和施工图纸确定好桥式方案之后,需要完成详细设计和施工图纸。
图纸的设计和编制出来记录了桥梁的具体尺寸、构造和建造方式等重要信息,有助于保证建造期间的准确施工,同时也方便了未来的维护管理。
总之,确定高速铁路桥梁桥式方案需要充分考虑各种因素,如结构荷载、桥跨、地质环境等,以确保桥式方案的稳固可靠、经济合理。
铁路桥台常见结构形式1. 引言铁路桥台是铁路桥梁结构中的重要组成部分,其作用是支撑和传递铁路桥梁的荷载,保证铁路线路的安全和稳定。
铁路桥台的结构形式多种多样,根据不同的设计要求和地理条件,可以选择不同的结构形式。
本文将介绍铁路桥台常见的结构形式,包括刚性桥台、弹性桥台和组合桥台。
2. 刚性桥台刚性桥台是最常见的铁路桥台结构形式之一。
它由混凝土或钢结构组成,具有较高的刚度和承载能力。
刚性桥台主要由桥台顶板、立柱和基础构成。
2.1 桥台顶板桥台顶板是刚性桥台的承载面,通常由预应力混凝土或钢板混凝土构成。
桥台顶板的厚度和尺寸根据设计要求和荷载计算来确定,以确保其具有足够的强度和刚度。
2.2 立柱刚性桥台的立柱通常由钢筋混凝土或钢结构构成。
立柱的数量和布置根据桥梁的跨度和荷载来确定,以保证桥台的稳定性和安全性。
2.3 基础刚性桥台的基础是支撑桥台的地基,通常采用混凝土浇筑或钢桩的形式。
基础的设计要考虑地质条件、荷载传递和抗震性能等因素,以确保桥台的稳定和安全。
3. 弹性桥台弹性桥台是一种较为特殊的桥台结构形式,其主要特点是具有一定的变形能力和减震效果。
弹性桥台通常由橡胶支座和钢板组成。
3.1 橡胶支座橡胶支座是弹性桥台的关键部件,它能够承受桥梁的荷载并减少震动传递。
橡胶支座具有较好的弹性和耐久性,能够吸收和分散桥梁的振动能量,减少对桥台和铁路线路的影响。
3.2 钢板弹性桥台的钢板位于橡胶支座的上方,用于传递桥梁的荷载。
钢板的选择要考虑其强度、刚度和耐久性等因素,以确保桥台的安全和稳定。
4. 组合桥台组合桥台是将刚性桥台和弹性桥台结合起来的一种桥台结构形式。
它兼具刚性桥台的承载能力和弹性桥台的减震效果,适用于特殊的工程要求和地理条件。
4.1 组合形式组合桥台的组合形式多种多样,可以根据具体的设计要求来确定。
常见的组合形式包括刚性桥台与弹性桥台的结合,以及刚性桥台与弹性桥台的分段布置。
4.2 优势组合桥台的优势在于既能满足桥梁的承载要求,又能减少对桥台和铁路线路的振动影响。
高速铁路桥梁的基本类型
高速铁路桥梁的基本类型包括以下几种:
1. 混凝土桥梁:混凝土桥梁是高速铁路常见的桥梁类型,具有良好的耐久性和承载能力。
根据结构形式可以分为板梁桥、T梁桥、箱梁桥等。
2. 钢桥:钢桥通常用于跨越较大跨度的河流或谷地,其优点在于施工周期短,适应能力强。
3. 悬索桥:悬索桥通过主梁上的吊杆将桥面悬挂在主塔上,可用于跨越宽广的水域或峡谷。
悬索桥在高速铁路中的使用相对较少,因为对线性和舒适性要求较高。
4. 拱桥:拱桥是一种古老且美观的桥梁结构,适用于中小跨度的桥梁。
在高速铁路中,也可采用一些特殊形式的拱桥。
5. 组合桥:某些情况下,会采用不同结构形式的组合桥,以充分利用各种结构的优点,满足特定的工程要求。
这些桥梁类型在高速铁路建设中,会根据跨度、地形、技术经济指标等因素进行选择,并可能结合实际情况采用多种结构形式的组合。
2020-2021中考数学锐角三角函数的综合热点考点难点附答案一、锐角三角函数1.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由(3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长.【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP的长为62或23.【解析】【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再根据直角三角形斜边中线等于斜边一半即可得OF=OE;(2)如图2中,延长EO交CF于K,由已知证明△ABE≌△BCF,△AOE≌△COK,继而可证得△EFK是等腰直角三角形,由等腰直角三角形的性质即可得OF⊥EK,OF=OE;(3)分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】(1)如图1中,延长EO交CF于K,∵AE⊥BE,CF⊥BE,∴AE∥CK,∴∠EAO=∠KCO,∵OA=OC,∠AOE=∠COK,∴△AOE≌△COK,∴OE=OK,∵△EFK是直角三角形,∴OF=12EK=OE;(2)如图2中,延长EO交CF于K,∵∠ABC=∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,∴∠BAE=∠CBF,∵AB=BC,∴△ABE≌△BCF,∴BE=CF,AE=BF,∵△AOE≌△COK,∴AE=CK,OE=OK,∴FK=EF,∴△EFK是等腰直角三角形,∴OF⊥EK,OF=OE;(3)如图3中,点P在线段AO上,延长EO交CF于K,作PH⊥OF于H,∵|CF﹣AE|=2,3AE=CK,∴FK=2,在Rt△EFK中,tan∠3∴∠FEK=30°,∠EKF=60°,∴EK=2FK=4,OF=12EK=2,∵△OPF是等腰三角形,观察图形可知,只有OF=FP=2,在Rt△PHF中,PH=12PF=1,3OH=23∴()2212362+-=如图4中,点P 在线段OC 上,当PO=PF 时,∠POF=∠PFO=30°, ∴∠BOP=90°, ∴OP=33OE=233, 综上所述:OP 的长为62 或233. 【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等,综合性较强,正确添加辅助线是解题的关键.2.小红将笔记本电脑水平放置在桌子上,显示屏OB 与底板OA 所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO '后,电脑转到AO 'B '位置(如图3),侧面示意图为图4.已知OA=OB=24cm ,O 'C ⊥OA 于点C ,O 'C=12cm . (1)求∠CAO '的度数.(2)显示屏的顶部B '比原来升高了多少?(3)如图4,垫入散热架后,要使显示屏O 'B '与水平线的夹角仍保持120°,则显示屏O 'B '应绕点O '按顺时针方向旋转多少度?【答案】(1)∠CAO′=30°;(2)(36﹣12)cm ;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°. 【解析】试题分析:(1)通过解直角三角形即可得到结果;(2)过点B 作BD ⊥AO 交AO 的延长线于D ,通过解直角三角形求得BD=OBsin ∠BOD=24×=12,由C 、O′、B′三点共线可得结果;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.试题解析:(1)∵O′C⊥OA于C,OA=OB=24cm,∴sin∠CAO′=,∴∠CAO′=30°;(2)过点B作BD⊥AO交AO的延长线于D,∵sin∠BOD=,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×=12,∵O′C⊥OA,∠CAO′=30°,∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°,∴O′B′+O′C﹣BD=24+12﹣12=36﹣12,∴显示屏的顶部B′比原来升高了(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,理由:∵显示屏O′B与水平线的夹角仍保持120°,∴∠EO′F=120°,∴∠FO′A=∠CAO′=30°,∵∠AO′B′=120°,∴∠EO′B′=∠FO′A=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.考点:解直角三角形的应用;旋转的性质.3.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定4.如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D 在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A 在点B的左侧),交y轴于点C,设点D的横坐标为a.(1)如图1,若m=.①当OC=2时,求抛物线C2的解析式;②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;(2)如图2,当OB=2﹣m(0<m<)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).【答案】(1) ①y=﹣x2+x+2.②.(2)P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【解析】试题分析:(1)①首先写出平移后抛物线C2的解析式(含有未知数a),然后利用点C (0,2)在C2上,求出抛物线C2的解析式;②认真审题,题中条件“AP=BP”意味着点P在对称轴上,“点B与点C到直线OP的距离之和最大”意味着OP⊥BC.画出图形,如图1所示,利用三角函数(或相似),求出a的值;(2)解题要点有3个:i)判定△ABD为等边三角形;ii)理论依据是角平分线的性质,即角平分线上的点到角两边的距离相等;iii)满足条件的点有4个,即△ABD形内1个(内心),形外3个.不要漏解.试题解析:(1)当m=时,抛物线C1:y=(x+)2.∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+)2).∴抛物线C2:y=﹣(x﹣a)2+(a+)2(I).①∵OC=2,∴C(0,2).∵点C在抛物线C2上,∴﹣(0﹣a)2+(a+)2=2,解得:a=,代入(I)式,得抛物线C2的解析式为:y=﹣x2+x+2.②在(I)式中,令y=0,即:﹣(x﹣a)2+(a+)2=0,解得x=2a+或x=﹣,∴B(2a+,0);令x=0,得:y=a+,∴C(0,a+).设直线BC的解析式为y=kx+b,则有:,解得,∴直线BC的解析式为:y=﹣x+(a+).假设存在满足条件的a值.∵AP=BP,∴点P在AB的垂直平分线上,即点P在C2的对称轴上;∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,∴OP⊥BC.如图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,则OP⊥BC,OE=a.∵点P在直线BC上,∴P(a,a+),PE=a+.∵tan∠EOP=tan∠BCO=,∴,解得:a=.∴存在a=,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP="BP"(3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+m)2).∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).∵OB=2﹣m,∴2a+m=2﹣m,∴a=﹣m.∴D(﹣m,3).AB=OB+OA=2﹣m+m=2.如图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB=,OE=OB﹣BE=﹣m.∵tan∠ABD=,∴∠ABD=60°.又∵AD=BD,∴△ABD为等边三角形.作∠ABD的平分线,交DE于点P1,则P1E=BE•tan30°=×=1,∴P1(﹣m,1);在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.在Rt△BEP2中,P2E=BE•tan60°=•=3,∴P2(﹣m,﹣3);易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2,且P3P4∥x轴.∴P3(﹣﹣m,3)、P4(3﹣m,3).综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,其坐标为:P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【考点】二次函数综合题.5.如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).(1)若△BDE是以BE为底的等腰三角形,求t的值;(2)若△BDE为直角三角形,求t的值;(3)当S△BCE≤92时,所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=23;(2秒或3秒;(3)6﹣【答案】(1)2【解析】【分析】(1)如图1,先由勾股定理求得AB的长,根据点A、E关于直线CD的对称,得CD垂直平分AE,根据线段垂直平分线的性质得:AD=DE,所以AD=DE=BD,由,可得t 的值;(2)分两种情况:①当∠DEB=90°时,如图2,连接AE,根据t的值;②当∠EDB=90°时,如图3,根据△AGC≌△EGD,得AC=DE,由AC∥ED,得四边形CAED 是平行四边形,所以AD=CE=3,即t=3;(3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE 面积的变化取决于以CE作底边时,对应高的大小变化,①当△BCE在BC的下方时,②当△BCE在BC的上方时,分别计算当高为3时对应的t的值即可得结论.【详解】解:(1)如图1,连接AE,由题意得:AD=t,∵∠CAB=90°,∠CBA=30°,∴BC=2AC=6,∴∵点A、E关于直线CD的对称,∴CD垂直平分AE,∴AD=DE,∵△BDE是以BE为底的等腰三角形,∴DE=BD,∴AD=BD,∴t=AD=;2(2)△BDE为直角三角形时,分两种情况:①当∠DEB=90°时,如图2,连接AE,∵CD垂直平分AE,∴AD=DE=t,∵∠B=30°,∴BD=2DE=2t,∴∴②当∠EDB=90°时,如图3,连接CE,∵CD垂直平分AE,∴CE=CA=3,∵∠CAD=∠EDB=90°,∴AC∥ED,∴∠CAG=∠GED,∵AG=EG,∠CGA=∠EGD,∴△AGC≌△EGD,∴AC=DE,∵AC∥ED,∴四边形CAED是平行四边形,∴AD=CE=3,即t=3;综上所述,△BDE为直角三角形时,t的值为3秒或3秒;(3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE 面积的变化取决于以CE作底边时,对应高的大小变化,①当△BCE在BC的下方时,过B作BH⊥CE,交CE的延长线于H,如图4,当AC=BH=3时,此时S△BCE=12AE•BH=12×3×3=92,易得△ACG≌△HBG,∴CG=BG,∴∠ABC=∠BCG=30°,∴∠ACE=60°﹣30°=30°,∵AC=CE,AD=DE,DC=DC,∴△ACD≌△ECD,∴∠ACD=∠DCE=15°,tan∠ACD=tan15°=t3=23,∴t=6﹣3由图形可知:0<t<6﹣3时,△BCE的BH越来越小,则面积越来越小,②当△BCE在BC的上方时,如图3,CE=ED=3,且CE⊥ED,此时S△BCE=12CE•DE=12×3×3=92,此时t=3,综上所述,当S△BCE≤92时,t的取值范围是6﹣3.【点睛】本题考查三角形综合题、平行四边形的判定和性质、直角三角形的性质、三角形的面积问题、轴对称等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,学会寻找特殊点解决问题,属于中考压轴题.6.2018年12月10日,郑州市城乡规划局网站挂出《郑州都市区主城区停车场专项规划》,将停车纳入城市综合交通体系,计划到2030年,在主城区新建停车泊位33.04万个,2019年初,某小区拟修建地下停车库,如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度为1:3,DE =3米,点C在DE上,CD=0.5米,CD是限高标志屏的高度(标志牌上写有:限高米),如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据2≈1.41,3≈1.73)【答案】该停车库限高约为2.2米.【解析】【分析】据题意得出3tan B ,即可得出tan A,在Rt△ADE中,根据勾股定理可求得DE,即可得出∠1的正切值,再在Rt△CEF中,设EF=x,即可求出x,从而得出CF3的长.【详解】解:由题意得,tan3B∵MN∥AD,∴∠A=∠B,∴tan A,∵DE⊥AD,∴在Rt△ADE中,tan A=DEAD,∵DE=3,又∵DC=0.5,∴CE=2.5,∵CF⊥AB,∴∠FCE+∠CEF=90°,∵DE⊥AD,∴∠A+∠CEF=90°,∴∠A=∠FCE,∴tan∠FCE=3.在Rt△CEF中,设EF=x,CF x(x>0),CE=2.5,代入得(52)2=x2+3x2,解得x=1.25,∴CFx≈2.2,∴该停车库限高约为2.2米.【点睛】本题考查了解直角三角形的应用,坡面坡角问题和勾股定理,解题的关键是坡度等于坡角的正切值.7.如图,AB是⊙O的直径,E是⊙O上一点,C在AB的延长线上,AD⊥CE交CE的延长线于点D,且AE平分∠DAC.(1)求证:CD是⊙O的切线;(2)若AB=6,∠ABE=60°,求AD的长.【答案】(1)详见解析;(2)9 2【解析】【分析】(1)利用角平分线的性质得到∠OAE=∠DAE,再利用半径相等得∠AEO=∠OAE,等量代换即可推出OE∥AD,即可解题,(2)根据30°的三角函数值分别在Rt△ABE中,AE=AB·cos30°,在Rt△ADE中,AD=cos30°×AE即可解题.【详解】证明:如图,连接OE,∵AE平分∠DAC,∴∠OAE=∠DAE.∵OA=OE,∴∠AEO=∠OAE.∴∠AEO=∠DAE.∴OE∥AD.∵DC⊥AC,∴OE⊥DC.∴CD是⊙O的切线.(2)解:∵AB是直径,∴∠AEB=90°,∠ABE=60°.∴∠EAB=30°,在Rt△ABE中,AE=AB·cos30°333在Rt△ADE中,∠DAE=∠BAE=30°,∴AD=cos30°×AE=32×3392.【点睛】本题考查了特殊的三角函数值的应用,切线的证明,中等难度,利用特殊的三角函数表示出所求线段是解题关键.8.如图,在正方形ABCD 中,E 是边AB 上的一动点,点F 在边BC 的延长线上,且CF AE =,连接DE ,DF ,EF . FH 平分EFB ∠交BD 于点H .(1)求证:DE DF ⊥;(2)求证:DH DF =:(3)过点H 作HM EF ⊥于点M ,用等式表示线段AB ,HM 与EF 之间的数量关系,并证明.【答案】(1)详见解析;(2)详见解析;(3)22EF AB HM =-,证明详见解析.【解析】【分析】(1)根据正方形性质, CF AE =得到DE DF ⊥.(2)由AED CFD △△≌,得DE DF =.由90ABC ∠=︒,BD 平分ABC ∠, 得45DBF ∠=︒.因为FH 平分EFB ∠,所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.(3)过点H 作HN BC ⊥于点N ,由正方形ABCD 性质,得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥,,得HM HN =.因为4590HBN HNB ∠=︒∠=︒,,所以22sin 45HN BH HN HM ===︒. 由22cos 45DF EF DF DH ===︒,得22EF AB HM =-. 【详解】(1)证明:∵四边形ABCD 是正方形,∴AD CD =,90EAD BCD ADC ∠=∠=∠=︒.∴90EAD FCD ∠=∠=︒.∵CF AE =。
路基与桩板结构下穿高速铁路桥梁影响对比分析[摘要]摘要:随着经济发展,越来越多的公路或城市道路下穿高速铁路桥梁,影响高速铁路桥梁稳定性。
高速铁路运行速度快,高铁桥梁结构变形超限将影响高速铁路运营安全,在设计阶段,应用大型有限元软件对道路下穿高速铁路进行影响分析是必要的,本文将对路基与桩板结构两种型式下穿高速铁路桥梁影响进行对比分析。
[关键词]关键词:道路下穿高铁;路基;桩板结构一、引言随着经济发展,越来越多的公路或城市道路下穿高速铁路桥梁,高速铁路作为国家运输大动脉,保证其运营安全十分重要,采取稳妥可靠的下穿方式、结构型式以及施工方法十分必要[1 5]。
高速铁路运行速度快,高铁桥梁结构变形过大将影响高速铁路运营安全,下穿构筑物(道路交通、管线等)的建设及使用已成为高速铁路运营安全的主要因素之一。
目前,道路穿越高铁的主要形式有路基下穿、桥梁下穿、桩板结构下穿、U型槽和框架结构等[2-3]。
其中路基下穿与桩板结构下穿适用于桥下填土高度不高的情形,本文结合工程实例,对这两种下穿型式进行对比分析。
二、工程实例拟建项目起自翠家岭村西、费县收费站西侧的G327上,向北沿规划G327,经北尹大桥西、成立庄东,在胡阳村南下穿日兰高速铁路后转向西,在农立庄西顺接方马路,向西经南东洲大桥南、荣和庄北、电厂南,止于北广丰村北的规划新西外环上。
道路全长26.667公里,道路等级为一级公路,道路路基宽度为25.5米,双向四车道,设计速度80km/h。
本工程穿越日兰高速铁路三和特大桥第108#孔,107#至109#孔桥梁为(60m+100m+60m)变截面连续箱梁,桥墩为圆端形实体桥墩,107#墩为桩基础,基础承台尺寸为9.6m×14.4m,108#墩为桩基础,基础承台尺寸为9.6m×14.4m。
(一)工程地质勘察深度范围内所揭露的地层以杂填土、粉质黏土、石灰岩、凝灰岩和泥岩为主,依据野外钻探资料,将所揭露地层分层叙述如下:第①层杂填土[Q42ml]:杂色,成分以粉质黏土为主,含有碎砖块和混凝土块,结构较差,局部为耕土。
高速铁路桥梁结构型式
高速铁路上的桥梁,应能在列车达到最高设计速度的条件下,满足行车安全和旅客乘坐的舒适度。
因而桥梁结构必须具有足够的强度、稳定性、刚度和耐久,并且保持桥上线路的平顺状态。
(一)桥梁结构体系
1.小跨度刚架桥的截面形式以现浇板梁为宜;简支梁与连续梁桥的截面以单箱单室箱梁为宜;板梁的截面推荐用日本高架桥的截面形状,箱梁截面推荐采用德国新干线标准设计截面。
钢桁架桥的桥面系以采用正交异性板为宜;组合梁桥也以箱形截面形状为宜。
2. 混凝土简支梁结构构造简单、技术成熟、架设快捷、更换方便,是我国既有铁路桥梁的主要型式,总数90%以上。
近年来,拼装式移动支架造桥机研制成功,使混凝土简支梁的跨度达56。
这就更
加扩大了铁路混凝土简支梁的使用范围。
在特殊条件下,其它型式的混凝土简支梁,如槽形梁等,也可采用。
3. 混凝土连续梁70年代以来,在我国新线铁路上修建了大量混凝土连续梁,以扩大混凝土梁桥的使用范跨度多在40~80m之间,最大达 84m,成为中等跨度铁路混凝土梁桥的主要型式。
作为一个实例,在小跨度范围内应用不多,钱塘江二桥的引桥,采用了7 ~9孔1联,共6孔跨度32 联47孔跨度32m等高度箱形截面双线铁路连续梁桥,是目前我国跨度最小的铁路预应力混凝土连续梁桥。
4. 混凝土刚架桥是一种空间超静定结构,整体性好,具有较好的刚度和抗震性能。
在日本高速铁路高架桥中占有十分重要的地位。
刚架桥多为3 ~ 5 孔一联,跨度 6 ~ 8 m 左右,联间以简支挂
孔相连。
填土高度7~12 m,基础多采用打入桩和扩大基础型式。
与我国京沪高速铁路沪宁段的线路和地质情况相近,具有较好的参考价值。
(二)上部结构型式
1. 分离式结构与整体式结构的比较。
在双线并列的情况下,梁部结构可采用两单线桥的分离式结构,也可采用双线桥整体式结构,对于中等跨度混凝土连续梁结构,考虑到一般采用悬臂灌注法施工。
尤其重要的是,双线单箱整体式结构,虽不能有效降低桥梁的动力系数,但从车辆运动平稳性考虑,由于结构自重增大,旅客乘坐舒适度有进一步改善,是值得重视的。
2.箱形截面和T形截面的比较。
箱形截面整体性强,抗扭刚度大是当代混凝土桥,特别是大跨度桥的主要形式。
它用于高速行车的桥梁上动力性能更显得优越。
这种截面形式混凝土梁的主要缺点是,在架设过程中需在桥位上进行梁片间的连结工作。
特别是对于高速铁路桥梁,当需进行工地横向预应力钢筋的张拉工作,费工费时,影响架桥进度。
分片式简支T梁是梁式桥构造简单,最易设计为各种标准跨径的装配式结构,施工工序少,架设程序固定,在多孔简支梁桥中,由于各跨构造和尺寸简化了施工管理工作,降低了施工费用,也便于养护和维修。
整孔简支箱梁在国外高速铁路中小跨度桥梁中常被采用,整孔简支箱梁具有受力简单、明确、型式简洁、外形美观、抗扭刚度
大、建筑高度相应较低、建成后的桥梁养护工作量小以及噪音小等优点。
(三)下部结构型式
为了节省工量,降低对地基的压力,减小基础尺寸和基桩的数量,对于中小跨桥梁宜采用轻型墩台,特别是对于多联孔的高架轻型墩台尚可增加建筑物外形的美观。
T形桥台的工量是耳墙式桥台的1.5~ 2.0倍,当然相应基础尺寸或承台基桩数量也会加所以除高地震区外,宜优先采用耳墙式桥台。
(四)高架桥的经济跨度分析
对于多跨联孔的高架桥来说,选择合理的跨度,使工程投资最小,是十分有意义的。
依据铁路工程概算定额,对采用打入直桩基础的各种跨度混凝土梁方案进行了计算,在三种填土高度情况下,各种跨度方案的造价相差不大。
高速铁路桥梁的特点
桥梁是构建铁路本体的重要基本工程结构之一,也是铁路建设的关键技术。
在高速运行的环境、技术要求以及我国特有的国情条件下,桥梁设计、建造和检测等许多方面具有与国外高速铁路以及我国传统铁路不同的要求和特点。
1、高架桥多、桥梁比例大
在高速铁路建设中,综合考虑建筑物与地基变形、控制工后沉降、少占良田、环境保护以及维修养护等多种因素,通过桥梁与路基工程的技术经济比较,加大桥梁比例,修建高架桥。
2、大量采用简支箱梁结构型式
刚度较大,整体性好。
高速铁路桥梁必须具有足够大的刚度性良好的整体性,以防止桥梁出现较大挠度和振幅。
同时,必须限制桥梁的预应力徐变上拱和不均匀温差引起的结构变形,以保证轨道的高平顺行。
纵向刚度大。
高速铁路要求依次铺设跨区间无缝线路,而桥上无缝线路钢轨的受力状态不同于路基,结构的温度变化、列车制动、桥梁挠曲会使桥梁在纵向产生一定位移,引起桥上钢轨产生附加应力。
结构便于检查维修。
3、特殊结构桥多
特殊结构桥桥梁的一般形式主要有:拱桥、连续刚构、V形刚构、斜拉桥、组合结构桥(如连续梁与拱组合桥、斜拉刚构组合桥、连续钢桁梁柔性拱组合桥等) 。
4、大跨度桥多
据统计,在建与拟建客运专线中, 100 m以上跨度的高速桥梁至少200 座以上。
其中,预应力混凝土连续梁桥的最大跨度为128 m,预应力凝
土刚构桥的最大跨度为180 m,钢桥最大跨度为504 m。
5、重视桥梁建筑美学
在桥梁设计构思时,除了考虑结构安全性与经济性之外,还同时从桥梁美学效果综合考虑桥梁形式美、功能美以及与环境的协调性,从时代的需求出发, 努力塑造新颖、美观的桥梁造型。
心中的理想建筑
理想中的建筑应在空间上通过几个大庭院的取光,以及白色环境反射加剧光亮的方式间接获得照明。
开敞的空间与家具的完美结合给人以宽敞整洁的感觉。
在整体设计上,我们希望用一种单纯的材料,以极致的设计语言,创造独特的感觉。
而建筑外观与室内空间也不是孤立存在的,而是相互交融,平衡和互补的关系。
建筑与空间本身应当形成视觉体验,其内部功能与形式能够激发人们对于艺术感知的渴望与热情。
整个建筑外观,照明,室内设计都力图做到表里如一。
灯光设计中,对于整体的光亮度和光的颜色需要特别考虑,控制在一个较低的亮度,选择温暖的亮色,使进到酒店的客人在第一时间可以放松下来。
建筑立面采用金色格栅,形体的序列感是为了呼应平行于建筑的解放大道高架桥的速度感与流动性。
从地下出入口,到公共走廊,再到入口大厅,随着空间尺度,建筑构件以及天花设备的变化,金色的
线条如流水一般在空间中穿行。
其形体的节奏感记录了所有空间轨迹,也反映了材料在不同空间状态中的视觉特征。
内外的统一性构筑了空间的特质。
现代城市的核心就是为市民提供具有活动和交流机会的城市公共空间体系。
而城市的特色多由它的令人瞩目的公共空间来决定。
在一个消费型的社会里,除了购物消费体验之外,商业建筑作为城市公共空间的一部分,其核心价值就在于通过创造独特的视觉感受,使人们对于城市有更深刻的归属感。
土木工程施工未来发展趋势
以最小的代价谋求经济效益与生态环境效益的最大化,是现代建筑技术活动的基本原则。
在这一原则的规范下,现代建筑技术的发展呈现出一系列重要趋势。
剖析和揭示这些发展趋势有助于认识和推动建筑技术的进步。
1.高技术化发展趋势
新技术革命成果向建筑领域的全方位、多层次渗透,是技术运动的现代特征,是建筑技术高技术化发展的基本形式。
这种渗透推动着建筑技术体系内涵与外延的迅速拓展,出现了结构精密化、功能多元化、布局集约化、驱动电力化、操作机械化、控制智能化、运转长寿
化的高新技术化发展趋势。
建材技术向高技术指标、构件化、多功能建筑材料方向发展。
在这种发展趋势中,工业建筑的施工技术也随之向着高科技方向发展,利用更加先进的施工技术,使整个施工过程合理化、高效化是工业建筑施工的核心理念。
2.生态化发展趋势
生态化促使建材技术向着开发高质量、低消耗、长寿命、高性能、生产与废弃后的降解过程对环境影响最小的建筑材料方向发展;要求建筑设计目标、设计过程以及建筑工程的未来运行,都必须考虑对生态环境的消极影响,尽量选用低污染、耗能少的建筑材料与技术设备,提高建筑物的使用寿命,力求使建筑物与周围生态环境和谐一致。
在这样的趋势中,建筑的灵活性将成为工业建筑施工技术首先要考虑的问题,在使用高科技材料的同时也要有助于周围生态的和谐发展,另外在建筑使用价值结束后建筑的本身对周围环境的影响也要在建筑施工的考虑之中。
3.工业化发展趋势
工业化是现代建筑业的发展方向。
它力图把互换性和流水线引入到建筑活动,以准化、工厂化的成套技术改造建筑业的传统生产方式。
从建筑构件到外部脚手架等都可以由工业生产完成,标准化的实施带来建筑的高效率,为今后的工业建筑施工技术的统一化提供了可能。