浙江省高考数学模拟试卷(含答案)
- 格式:docx
- 大小:484.40 KB
- 文档页数:18

2018年高考模拟试卷语文卷
注意事项:
1.本试卷共8页,满分为150分,考试用时为150分钟。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色签字笔写在试卷及答题卡上。
3.请认真核对学校、姓名、准考证号。
4.作答非选择题,必须用0.5毫米黑色签字笔在答题纸上的指定位置作答,在其他位置作答一律无效。
一、语言文字运用(共20分)
【改编】1.下列各句中,没有错别字且加点字的注音全部正确的一项是(3分) ( ▲ )
A.《战狼2》是一部商业和主弦律两不误的电影。一方面,各种打斗、爆炸场面看得人肾上腺素狂飙(biāo);另一方面,故事本身又能唤起人们内心的爱国主义热情,使观众同时得到了视觉和心灵上的震(zhèn)撼,可以说是一次满足两个愿望。
B.今年银监系统对违规行为开逾(yù)1500张罚单,上半年整体罚款规模近3.4亿元。银监风暴之下,违规行为无处遁(dùn)形。
C.圣彼得堡城风光旖旎(nǐ),教堂建筑气势雄伟,构思精巧,设计细腻大方,外墙及立柱均使用大理石、花岗岩精心雕刻成。整座教堂显得金碧辉煌,熠(yì)熠生辉,使人赏心悦目,美不胜收。
D.晕(yūn)车与内耳中的前庭系统有很大关系,当前庭器官受到长时间过强的刺激,抑或刺激虽未过强但前庭过于敏感使,就会出现眩(xuàn)晕等症状。
【命题意图】本题考查识记现代汉语普通话的字音、字形,能力层级为A。近几年高考对字形的考查都置于具体的语境中,应用性强。所选的字音、字形均为现实生活中的常见易错字。
阅读下面文字,完成2-3题。
敬畏是人生的大智慧,不仅是一种人生态度,也是..一种行为准则。〔甲〕曾国藩说自己平生有“三畏”:畏天命、畏人言、畏君父。他的一生始终常怀敬畏之心,坚守做人为官的基本规律..,保持清醒的头脑,做到原则不动、底线不松,在战战兢兢、如履薄冰的心境中度过,最终一路平步青云,大业辉煌,成就了自我。

试卷第 1 页 (共3页)
高考数学模拟试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分, 考试用时120分钟.
第Ⅰ卷(选择题 共50分)
参考公式:
如果事件A、B互斥, 那么 柱体(棱柱、圆柱)的体积公式
P(A+B)=P(A)+P(B) hVS柱体
如果事件A、B相互独立, 那么 其中S表示柱体的底面积,
P(A·B)=P(A)·P(B) h表示柱体的高
一、单项选择题:(每一小题仅有一个正确答案, 请将正确答案的代号填入
答题表内。每小题5分, 共计60分)
1.下列关系中正确的是 ( )
A. 0 B.a{a} C.{a,b}{b,a} D. }0{
2. 不等式21xx的解集为 ( )
A. )0,1[ B. ),1[
C. ]1,( D. ),0(]1,(
3.对任意实数,,abc在下列命题中, 真命题是( )
A. ""acbc是""ab的必要条件 B. ""acbc是""ab的必要条件
C. ""acbc是""ab的充分条件 D. ""acbc是""ab的充分条件
4.若平面向量b与向量)2,1(a的夹角是o180, 且53||b, 则b( )
A. )6,3( B. )6,3(
C. )3,6( D. )3,6(
5.设P是双曲线19222yax上一点, 双曲线的一条渐近线方程为023yx, 1F、2F分别是双曲线的左、右焦点。若3||1PF, 则||2PF ( )
A. 1或5 B. 6 C. 7 D.9

微信公众号:“浙江数学”提醒您,答案请仔细核对后使用,仅供参考
第1页(共29页)绝密★启用前
2018年浙江省高考数学试卷
考试时间:120分钟;试卷整理:微信公众号--浙江数学
学校:___________姓名:___________班级:___________考号:___________
题号一二三总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷(选择题)
评卷人得分
一.选择题(共10小题,满分40分,每小题4分)
1.(4分)(2018•浙江)已知全集U={1,2,3,4,5},A={1,3},则∁
UA=()
A.∅B.{1,3}C.{2,4,5}D.{1,2,3,4,5}
2.(4分)(2018•浙江)双曲线﹣y2=1的焦点坐标是()
A.(﹣,0),(,0)B.(﹣2,0),(2,0)C.(0,﹣),(0,)D.(0,
﹣2),(0,2)
3.(4分)(2018•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积
(单位:cm3)是()微信公众号:“浙江数学”提醒您,答案请仔细核对后使用,仅供参考
第2页(共29
页)A.2B.4C.6D.8
4.(4分)(2018•浙江)复数(i为虚数单位)的共轭复数是()
A.1+iB.1﹣iC.﹣1+iD.﹣1﹣i
5.(4分)(2018•浙江)函数y=2|x|sin2x的图象可能是()
A
.B
.C
.D
.
6.(4分)(2018•浙江)已知平面α,直线m,n满足m⊄α,n⊂α,则“m∥n”是“m∥α”
的()
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
7.(4分)(2018•浙江)设0<p<1,随机变量ξ的分布列是
ξ012
P
则当p在(0,1)内增大时,()
A.D(ξ)减小B.D(ξ)增大微信公众号:“浙江数学”提醒您,答案请仔细核对后使用,仅供参考
第3页(共29页)C.D(ξ)先减小后增大D.D(ξ)先增大后减小

第1页,共23页
高考语文模拟试卷(4)
题号 一 二 三 四 五 六 七 总分
得分
一、默写(本大题共1小题,共3.0分)
1. 补写出下列名篇名句的空缺部分。
(1)凤兮!凤兮!何德之衰!______,______。(《论语》)
(2)盖将自其变者而观之,______;自其不变者而观之,______。(苏轼《赤壁赋》)
(3)间关莺语花底滑,幽咽泉流冰下难。______,______。(白居易《琵琶行》)
(4)斜阳草树,寻常巷陌,______。想当年,金戈铁马,______。(辛弃疾《永遇乐•京口北固亭怀古》)
(5)亲朋无一字,老病有孤舟,______,______。(杜甫《登岳阳楼》)
二、选择题(本大题共2小题,共6.0分)
2. 下列各句中,没有错别字且注音全都正确的一项是( )
A. “抢跑式”校外培训班喧宾夺主,主要原因在于义务教育优质资源分布不均衡(héng),这种不均衡导致一些中小学校与校外培训机构互相钩连,将培训结果与中小学校招生入学挂钩。
B. 教育事业绝不是一个人的独行,团队协作、分工明确、高效执行、目标一致是做成任何事业的必备前提,唯有如此,才能在于浑沌处亮一盏明灯,做教育行业中“口碑(bēi)票房”双丰收的《红海行动》。
C. 水受重力驱动,总要往低处流,且荡平阻挡、充盈凹陷,秉(bǐng)持温良向善;沙则借风力助推,偏爱往高处攀,且积沙成峰、摧枯拉朽(xiǔ),始终前赴后继。
D. 中国在外交斡(wò)旋过程中提出的一系列理念和方案,体现了中国与世界各国共同发展、休戚(qì)与共的态度和决心,也体现了中国作为大国的使命感和责任感。
3. 下列各句中,没有语病的一项是( )
A. PM2.5俨然已成为中国当下最敏感的话题之一,1月30日全国雾霾面积已达到143万平方公里,社会各界呼吁尽快出台治理空气污染,各城市和地区开始探索治霾之道。

第1页,共16页
高考数学模拟试卷(4月份)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,共40.0分)
1. 若集合A={x|x2-1≥0},B={x|0<x<4},则A∩B=( )
A. (-∞,-1) B. [0,4) C. [1,4) D. (4,+∞)
2. 已知i为虚数单位,,则z的虚部为( )
A. 1 B. -2 C. 2 D. -2i
3. 已知双曲线C:-=1(a>0,b>0)的渐近线方程为y=±x,则双曲线C的离心率为( ) A. B. C. D.
4. 函数函数的大致图象为( )
A. B.
C. D.
5. 已知随机变量ξ满足P(ξ=0)=x,P(ξ=1)=1-x,若,则( )
A. E(ξ)随着x的增大而增大,D(ξ)随着x的增大而增大
B. E(ξ)随着x的增大而减小,D(ξ)随着x的增大而增大
C. E(ξ)随着x的增大而减小,D(ξ)随着x的增大而减小
D. E(ξ)随着x的增大而增大,D(ξ)随着x的增大而减小
6. 某几何体的三视图如图所示,则该几何体的体积是( )
A.
B.
C.
D.
第2页,共16页
7. “”是“”的( )
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
8. 如图,圆O是半径为1的圆,,设B,C为圆上的任意2个点,则的取值范围是( ) A.
B. [-1,3]
C. [-1,1] D.
9. 在棱长为的正四面体D-ABC中,过点D的平面Γ与底面ABC所成锐二面角的正切值为,设平面Γ与底面ABC的交线为l,当平面Γ运动时,直线l在△ABC内的部分形成的区域的面积为( ) A. B. C. D.
10. 已知二次函数f(x)=ax2+bx+c有零点,且a+b+c=1,则max{min{a,b,c}}=( ) A. B. C. D.

2011年宁波高三“十校联考”
数学(理科)试题
命题学校:北仑中学 宁海中学
说明:
1、本试卷分选择题 和非选择题两部分,共150分,考试时间120分钟。
2、请将答案全部填写在答题卡上。
选择题部分(共50分)
一、选择题:本题共10小题,每小题5分,共50分,在每小题出的四个选项中,只有一项是符合题目要求的。
1.设集合}0log|{},01|{22xxBxxA,则等于BA( )
A.}1|{xx B.}0|{xx C.}1|{xx D.}11|{xxx或
2.若命题甲:32yx或;命题乙:5yx,则( )
A.甲是乙的充分非必要条件
B.甲是乙的必要非充分条件;
C.甲是乙的充分条件;
D.甲既不是乙的充分条件,也不是乙的必要条件
3.某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如右图所示,则中位数与众数分别为( )
A.23,21
B,23,23
C.23,25
D.25,25
4.已知m,n为直线,,为平面,给出下列命题( )
①anmam// ②nmnm//
③//amam ④nmanam////
其中的正确命题序号是( )
A.③④ B.②③ C.①② D.①②③④
5.设双曲线以椭圆192522yx长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的离心率为( )
A.2 B.25 C.23 D.26
6.某程序框图如右图所示,现输入如下四个函数,则可以输出的函数是( )
A.2)(xxf B.xxf1)(
C.xexf)( D. xxfsin)(
7.已知函数xxxhxxxgxxfx32)(,log)(,2)(的零点依次为cba,,,则cba,,的大小顺序正确的是( )

试卷第 1 页 (共3页)
高考数学模拟试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分, 考试用时120分钟.
第Ⅰ卷(选择题 共50分)
参考公式:
如果事件A、B互斥, 那么 柱体(棱柱、圆柱)的体积公式
P(A+B)=P(A)+P(B) hVS柱体
如果事件A、B相互独立, 那么 其中S表示柱体的底面积,
P(A·B)=P(A)·P(B) h表示柱体的高
一、单项选择题:(每一小题仅有一个正确答案, 请将正确答案的代号填入
答题表内。每小题5分, 共计60分)
1.下列关系中正确的是 ( )
A. 0 B.a{a} C.{a,b}{b,a} D. }0{
2. 不等式21xx的解集为 ( )
A. )0,1[ B. ),1[
C. ]1,( D. ),0(]1,(
3.对任意实数,,abc在下列命题中, 真命题是( )
A. ""acbc是""ab的必要条件 B. ""acbc是""ab的必要条件
C. ""acbc是""ab的充分条件 D. ""acbc是""ab的充分条件
4.若平面向量b与向量)2,1(a的夹角是o180, 且53||b, 则b( )
A. )6,3( B. )6,3(
C. )3,6( D. )3,6(
5.设P是双曲线19222yax上一点, 双曲线的一条渐近线方程为023yx, 1F、2F分别是双曲线的左、右焦点。若3||1PF, 则||2PF ( )
A. 1或5 B. 6 C. 7 D.9
6、原点到直线y=kx+2的距离为2, 则k的值为 ( )

1 / 12
高三数学高考仿真模拟
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个选项符合题目要求。
1.己知复数z满足(1-i)z=2i(i为虚数单位),则z=( )
A.-1-i B.-1+i C.1+i D.1-i
2.若集合M={x|x>1},N={xZ|0≤x≤4},则(CRM)∩N=( )
A.{0} B.{0,1} C.{0,1,2} D.{2,3,4
3.在矩形ABCD中,|AB|=4,|AD|=2.若点M,N分别是CD,BC的中点,则AM·AN=( )
A.4 B.3 C.2 D.1
4.函数xf是定义在R上的奇函数,41f=1,当x<0时,xf=log2x-+m,则实数m=( )
A.-1 B.0 C.1 D.2
5.在平面直角坐标系xOy中,角的顶点在原点,始边与x轴的非负半轴重合,终边经过点(-3,1),则cos2=( )
A.53- B.53 C.54- D.54
6.执行如图所示的程序框图,则输出的结果是( )
A.8 B.16 C.32 D.64
7. 已知a,bÎR,“ab>0”是“ba+ab>2”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
8. 已知函数fx()=sinwx+j()w>0,j
的图象向右平移p6个单位长度后,得到的图象关于y轴对称,则( )
A.fx()的图象关于点p6,0æèçöø÷对称 B.fx()的图象关于点-p6,0æèçöø÷对称
C.fx()在-p6,p3æèçöø÷单调递增 D.fx()在-2p3,-p6æèçöø÷单调递增

第1页,共25页 高考语文模拟试卷(4月份)
题号 一 二 三 四 五 六 七 八 总分
得分
一、选择题(本大题共2小题,共6.0分)
1. 下列各句中,没有错别字且加点字的注音全都正确的一项是( )
A. 可与西方大片媲.( bì)美的震撼特效,契合民族感情、彰显国家精神的内容,使得《流浪地球》的票房能在竞争激烈的春节档.( dàng)期中独占鳌头。
B. 皎沽的月光爬上鎏.(liú)金宝顶,绵延的灯彩映出角楼的瑰.( guī)丽,绚烂的灯光秀把城楼照得璀璨--历经沧桑的故宫沉浸在一片喜庆祥和之中。
C. 把握中国思想文化的荦.(luó)荦大端,从中汲取精髓.(suí)并加以淬炼,一定能为新时代文艺创作提供丰厚底蕴和淋漓原气。
D. 没有甄别地乱用、滥用网络词语,将造成语言系统混.( hūn)乱,妨碍交流;对网络词语嗤之以鼻,摒.( bìng)弃不用,会削弱表达的时代性与鲜活味。
2. 下列各句中,没有语病的一项是( )
A. 旷日持久的“脱欧”行动使英围航空、餐饮、制造、运输等多行业受到冲击,加深了民众的焦虑感,多方压力让英国政府进退两难。
B. 于教授擅写人物,她用诗意的文字、散文的笔法,将记忆中的人物与历史事件、眼前景物结合,创造出一系列血肉丰满的艺术形象。
C. 房地产行业关涉社会政治、经济的方方面面,期望通过一个想法或意见的出台解决目前市场存在的诸多问题是不现实的。
D. 智能手机在学生群体中迅速普及引发的一系列问题,是全面禁止还是合理引导,是刚性约束还是柔性管理,成为考验学校和教师的难题。
二、默写(本大题共1小题,共6.0分)
3. 补写出下列名篇名句的空缺部分。
仰之弥高, ______ 。瞻之在前 ______ 。(《论语》)
且臣少仕伪朝, ______ ;本图宦官达 ______ 。(李密《陈情表》)
______ ,万夫莫开。(李白《蜀道难》)
第1页,共15页
高考数学模拟试卷(5月份)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,共30.0分)
1. 已知集合M={x∈Z|x2-2x<8},P={1,3},Q={0,7},则Q∪(∁MP)=( )
A. {0,1,7} B. {-1,0,7} C. {0,1,3,7} D. {-1,0,2,7}
2. 双曲线9x2-16y2=1的焦点坐标为( )
A. (±,0) B. (0,) C. (±5,0) D.
(0,±5)
3. 已知i为虚数单位,设z=1+,则复数z在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
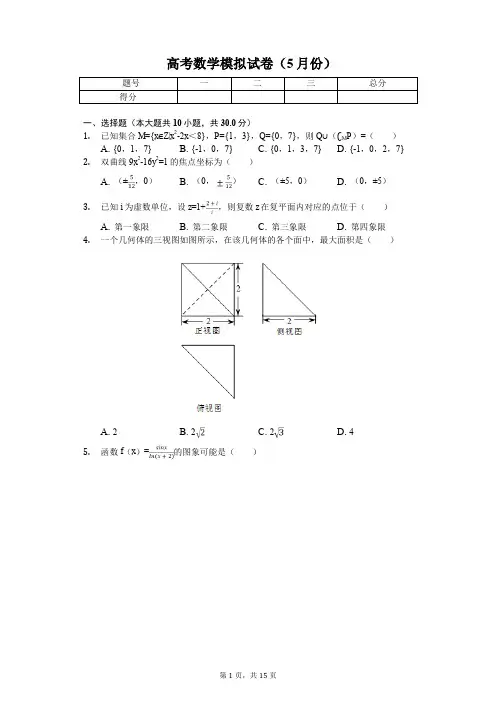
4. 一个几何体的三视图如图所示,在该几何体的各个面中,最大面积是( )
A. 2 B. 2 C. 2 D. 4
5. 函数f(x)=的图象可能是( ) 第2页,共15页 A. B.
C. D.
6. 下面四个命题中正确的是( )
A. “直线a、b不相交”是“直线a、b为异面直线”的充分非必要条件
B. “l⊥平面α”是“直线l垂直于平面α内无数条直线”的充要条件
C. “a垂直于b在平面α内的射影”是“直线a⊥b”的充分非必要条件
D. “直线a平行于平面β内的一条直线”是“直线a∥平面β”的必要非充分条件
7. 已知随机变量ξ满足P(ξ=0)=,P(ξ=1)=x,P(ξ=2)=-x.若0<x<.则( )
A. E(ξ)随着x的增大而增大,D(ξ)随着x的增大而增大
B. E(ξ)随着x的增大而减小,D(ξ)随着x的增大而增大
C. E(ξ)随着x的增大而减小,D(ξ)随着x的增大而减小
D. E(ξ)随着x的增大而增大,D(ξ)随着x的增大而减小
8. 在长方体ABCD-A1B1C1D1中,底面ABCD是边长为3的正方形,侧棱AA1=x,P为矩形CDD1C1内部(含边界)一点,M为BC中点,∠APD=∠CPM,三棱锥A1-PCD的体积的最大值记为V(x),则关于函数V(x),下列结论正确的是( )

第1页,共16页
浙江省高考数学模拟试卷(10)(4月份)
一、单选题(本大题共10小题,共40.0分)
1. 已知集合𝐴={𝑥|𝑥2<1},𝐵={𝑥|log2𝑥<0},则𝐴∪𝐵=( )
A. (−∞,1) B. (0,1) C. (−1,0) D. (−1,1)
【答案】D
【解析】解:集合𝐴={𝑥|𝑥2<1}=(−1,1),𝐵={𝑥|log2𝑥<0}=(0,1),
则𝐴∪𝐵=(−1,1),
故选:D.
化简集合,再求并集.
考查集合的并集运算,基础题.
2. 已知𝑡𝑎𝑛𝛼=2,则1+𝑠𝑖𝑛2𝛼+cos2𝛼sin2𝛼−2𝑐𝑜𝑠2𝛼=( )
A. 32 B. 52 C. 4 D. 5
【答案】D
【解析】解:∵𝑡𝑎𝑛𝛼=2,
∴1+𝑠𝑖𝑛2𝛼+cos2𝛼sin2𝛼−2𝑐𝑜𝑠2𝛼=sin2𝛼+2𝑠𝑖𝑛𝛼𝑐𝑜𝑠𝛼+2𝑐𝑜𝑠2𝛼sin2𝛼−2𝑐𝑜𝑠2𝛼=tan2𝛼+2𝑡𝑎𝑛𝛼+2tan2𝛼−2=22+2×2+222−2=5.
故选:D.
由已知利用同角三角函数基本关系式,二倍角的正弦函数公式化简所求即可求解.
本题主要考查了同角三角函数基本关系式,二倍角的正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.
3. 圆𝑥2+𝑦2−𝑚𝑥+𝑦+𝑚=0在x轴上截得的弦长是它在y轴上截得的弦长的2倍,则实数m的值是( )
A. −6−2√10 B. −6+2√10 C. −3−√10 D. −3+√10
【答案】A
【解析】解:对于𝑥2+𝑦2−𝑚𝑥+𝑦+𝑚=0,
令𝑥=0得:𝑦2+𝑦+𝑚=0,设与y轴交点的纵坐标为𝑦1,𝑦2,且1−4𝑚>0,得𝑚<14①.
则𝑦1+𝑦2=−1,𝑦1𝑦2=𝑚,故与y轴相交的弦长为:|𝑦1−𝑦2|=√(𝑦1+𝑦2)2−4𝑦1𝑦2=√1−4𝑚. 第2页,共16页 同理,令𝑦=0可得:𝑥2−𝑚𝑥+𝑚=0,设与x轴交点的横坐标为𝑥1,𝑥2,且𝑚2−4𝑚>0,得𝑚>4,或𝑚<0②.
第1页,共19页
高考语文模拟试卷(一)
题号 一 二 三 四 五 六 总分
得分
一、默写(本大题共1小题,共5.0分)
1. 补写出下列名篇名句中的空缺部分。
(1)哀吾生之须臾,______。(苏轼《赤壁赋》)
(2)______,斯天下之民至焉。(孟子《寡人之于国也》)
(3)盘盘焉,囷囷焉,蜂房水涡,______。(杜牧《阿房宫赋》)
(4)无边落木萧萧下,______。(杜甫《登高》)
(5)多情应笑我,早生华发。人间如梦,______。(苏轼《念奴娇•赤壁怀古》)
二、选择题(本大题共10小题,共30.0分)
2. 下列词语中加点字的注音全都正确的一项是( )
A. 喧嚣.(xiāo) 濡.染(rú) 教诲.(huǐ) 胡诌.(zhōu)
B. 剥蚀.(shí) 蓓.蕾(pèi) 隽.永(juàn) 矗.立(chù)
C. 桦.树(huà) 老饕.(tāo) 铿.锵(kēng) 猝.然(cù)
D. 昵.称(ní) 谗.言(chán) 气氛.(fēn) 嗜.好(shì)
3. 下列词语中没有错别字的一项是( )
A. 甘之如怡 自我安慰 哀怨 截瘫
B. 半途而费 窸窸窣窣 祭坛 雕栏
C. 旁征博引 九坛八庙 安详 车辙
D. 撕叫不停 骄阳高悬 倔强 羞涩
4. 依次填入下列句子横线处的词语,恰当的一项是( )
(1)如果我们想在疾病________起来以前根除它们,就必须毫不留情地揭露它们。
(2)他的创作是如此博大精深,又是如此有意识地自成一体,因此,可以毫无愧色地说,他的艺术是世界文化中不容________的组成部分。
(3)太阳黑子又进入集中爆发期,我国天文学家从去年就开始密切________太阳的活动。
A. 蔓延 置疑 监测 B. 曼延 置疑 观测
第1页,共16页
中考语文模拟试卷
学校:___________姓名:___________班级:___________考号:___________
一、默写(本大题共1小题,共8.0分)
1. 古诗文名句默写。
(1)潮平两岸阔, ______ 。(王湾《次北固山下》)
(2)抽刀断水水更流, ______ 。(李白《宣州谢朓楼饯别校书叔云》)
(3) ______ ,铁马冰河入梦来。(陆游《十一月四日风雨大作》)
(4) ______ ,日长蝴蝶飞。(冯延巳《醉桃源》)
(5)故天将降大任于是人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,
______ , ______ ,曾益其所不能。(《孟子•告子下》)
(6)快毕业了,美好的祝愿总是说不完。新锐同学想找一句古诗送给他的同窗好友,希望好友在未来的学习中百尺竿头更进一步,请你帮他想一句。你想到的句子是: ______ , ______ 。
二、其他(本大题共1小题,共4.0分)
2. 读下面这段文字,根据拼音写出汉字。
中国是一个文化资源大国,处处都可以找到(yùn) ______ 藏了几千年历史信息的文化资源,既有传统的,也有现代的;既有显性的,也有隐性的;既有(bīn)
______ 危的,也有新生的,林林总总,不一而足。不同地区、不同社群之间的文化习惯、文化形态也参差多样,勾连交错,互相(shèn) ______ 透,形成万花筒般变化多(zī) ______ 的文化生态。
三、选择题(本大题共1小题,共3.0分)
3. 下列加点的文言词语意思相同的一项是( )
A. 学而不思则罔,思而不学则 殆. 此 殆.天所以资将军,将军岂有意乎
B. 忠之 属.也,可以一战 土地平旷,屋舍俨然,有良田美池桑竹之 属.
C. 予观夫巴陵 胜.状,在洞庭一湖 白头搔更短,浑欲不 胜.簪
2020年浙江省高考数学模拟试卷(4月份)
一.选择题(共10小题)
1.设集合A={x∈N||x|<4},B={x|2x≤4},则A∩B=( )
A.{x|x≤2} B.{x|﹣4<x≤2} C.{0,1,2} D.{1,2}
2.设复数z满足iz=2+3i,其中i为虚数单位,在复平面内,复数z对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知q是等比数列{an}的公比,首项a1<0,则“0<q<1”是“数列{an}是递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.设x,y满足,则|x+4y|的最大值为( )
A.0 B.1 C.2 D.5
5.函数y=﹣cosxln|x|的图象可能是( )
A. B.
C. D. 6.随机变量X满足P(X=p)=p,P(X=1﹣p)=1﹣p,随机变量Y=1﹣X,则( )
A.E(X)≥E(Y),D(X)≥D(Y) B.E(X)≥E(Y),D(X)=D(Y
C.E(X)≤E(Y),D(X)≥D(Y) D.E(X)≤E(Y),D(X)=D(Y)
7.已知正四面体ABCD中,E,F分别是线段BC,BD的中点,P是线段EF上的动点(含端点).PA与平面BCD所成的角为θ1,二面角A﹣EF﹣D的平面角为θ2,二面角A﹣CD﹣B的平面角为θ3,则( )
A.θ1≤θ3≤θ2 B.θ3≤θ1≤θ2
C.θ1≤θ2,θ1≤θ3 D.θ1≤θ3,θ2≤θ3
8.已知双曲线的左、右焦点分别为F1,F2,P是双曲线上一点,满足|PF1|=|F1F2|,PF2与双曲线的一条渐近线平行,则该双曲线的离心率是( )
A. B. C. D.3
9.已知a∈R,函数f(x)=,则函数y=f(x)的零点个数不可能为( )
A.0 B.1 C.2 D.3
10.已知数列{an}满足:a1=1,.
新高考数学模拟试卷(含答案)
一、选择题
1.如图所示的圆锥的俯视图为( )
A. B. C. D.
2.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数学之和为偶数的概率是( )
A.12 B.13 C.23 D.34
3.已知532()231fxxxxx,应用秦九韶算法计算3x时的值时,3v的值为( )
A.27 B.11 C.109 D.36
4.给出下列说法:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确说法的个数是( )
A.0 B.1 C.2 D.3
5.在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为
A.10 B.11 C.12 D.15
6.在△ABC中,AD为BC边上的中线,E为AD的中点,则EB
A.3144ABAC B.1344ABAC
C.3144ABAC D.1344ABAC
7.若,是一组基底,向量=x+y (x,y∈R),则称(x,y)为向量在基底,下的坐标,现已知向量在基底p=(1,-1), q=(2,1)下的坐标为(-2,2),则在另一组基底m=(-1,1), n=(1,2)下的坐标为( )
A.(2,0) B.(0,-2) C.(-2,0) D.(0,2)
8.下列各组函数是同一函数的是( )
①32fxx与2fxxx;3fx2xyx2x与②fxx与2gxx;
③0fxx与01gxx;④221fxxx与221gttt.
浙江省2020届高考语文模拟试卷
语 文
考生须知:
1.本卷满分150分,考试时间150分钟;
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。
3.所有答案必须写在答题卷上,写在试卷上无效;
4.考试结束后,只需上交答题卷。
一、语言文字运用(共20分)
1.下列各句中,没有错别字且加点字的注音全都正确的一项是(3分)( )
A.贺岁档(dàng)的常胜将军的新电影《只有芸知道》,上映7天,票房勉强过亿。对此,他发文感慨:“一众新锐导演生龙活虎,催营拔寨(zhài),屡创新高,我已是英雄老矣!”
B.行进中的中国,给了你最大的底气。这份底气,藏在你眼中绽放的神采里;镌(jun)刻进你为生活打拼(pn)、为理想执着的自信里;映照在你的谈吐,你的胸襟你的视野里。
C.如果对文艺事业没有深厚情谊(yì),缺乏传世之心,仅仅当作谋生的手段、牟利的工具,这样的文艺工作就容易沾满铜臭(chòu)味,这样的文艺工作者就容易成为市场的奴隶。
D.淖(nào),是一片大水。说是湖泊,似还不够,比一个池塘可要大得多,淖中央有一条狭长的沙洲。沙洲上长满茅草和芦荻。春初水暖,沙洲上冒出很多紫红色的芦芽和灰绿色的蒌蒿(go)。
阅读下面的文字,完成下面2~3小题。
经典是在古今中外浩如烟海的书籍中淘洗出的精品,经受了不同时代、不同人群从不同的视角去审视和诠释。然而,在现实生活中,大学生经典阅读的现状并不乐观。【甲】近日,华东师范大学在上海书展期间发布了“2019新时代上海大学生经典阅读指数报告”。其中数据显示,大学生经典阅读的范围比较狭隘,经常阅读文学类经典的学生尚不足三成,而有三至四成的学生从不读哲学、教育学和法学类经典。其次是经典阅读愈加浅层化。【乙】具体表现为快餐式和功利式的阅读,人们越来越不愿认真、耐心阅读,而转向浏览网页式的跳读和浏览,经典往往读得支离破碎。最后是缺乏经典阅读的氛围。学校教学过程中重知识传授和技能掌握,校园缺乏人文内涵。同时,家庭普遍缺乏读书氛围,不读书、读书少的家长不在少数。
第1页,共18页
浙江省高考数学模拟试卷(含答案)
一、单选题(本大题共10小题,共40.0分)
1. 已知集合𝐴={𝑥|𝑥2−2𝑥≤0},𝐵={𝑥|0≤log3𝑥≤9},𝐶={𝑥|𝑥=2𝑛,𝑛∈𝑁},则𝐴∩𝐵∩𝐶=( )
A. {2} B. {0,2} C. {0,2,4} D. {2,4}
【答案】A
【解析】解:集合𝐴={𝑥|𝑥2−2𝑥≤0}={𝑥|0≤𝑥≤2}=[0,2],
𝐵={𝑥|0≤log3𝑥≤9}={𝑥|1≤𝑥≤2}=[1,2],
𝐶={𝑥|𝑥=2𝑛,𝑛∈𝑁}={0,2,4,…},
则𝐴∩𝐵∩𝐶={2}.
故选:A.
化简集合A、B、C,根据交集的定义计算即可.
本题考查了集合的化简与运算问题,是基础题.
2. 复数z满足(𝑧−2𝑖)⋅(1+𝑖)=2(𝑖为虚数单位),则复数𝑧−在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】D
【解析】解:由(𝑧−2𝑖)⋅(1+𝑖)=2得:𝑧−2𝑖=21+𝑖=1−𝑖,
∴𝑧=1+𝑖,𝑧−=1−𝑖.则𝑧−对应的点(1,−1)在第四象限,
故选:D.
先求出z,然后求出z的共轭复数,由此即可求解.
本题考查了共轭复数的概念,考查了复数对应的点的位置,属于基础题.
3. 如果点𝑃(𝑥,𝑦)在平面区域{2𝑥−𝑦+2≥0𝑥−2𝑦+1≤0𝑥+𝑦−2≤0上,则𝑦+1𝑥−2的取值范围是( )
A. [−2,−13] B. [−2,−32] C. [−2,13] D. [−13,2]
【答案】A
【解析】解:如图,先作出点𝑃(𝑥,𝑦)所在的平面区域. 第2页,共18页 𝑦+1𝑥−2表示动点P与定点𝑄(2,−1)连线的斜率.
联立{𝑥−2𝑦+1=0𝑥+𝑦−2=0,解得{𝑥=1𝑦=1.
于是𝑘𝑄𝐸=1+11−2=−2,𝑘𝑄𝐹=0+1−1−2=−13.
因此−2≤𝑦+1𝑥−2≤−13.
故选:A.
作出不等式组对应的平面区域,利用𝑦+1𝑥−2的几何意义,通过数形结合即可的得到结论.
本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键,是中档题.
4. 条件p:𝑥2−4𝑥−5<0是条件q:𝑥2+6𝑥+5>0的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 非充分又非必要条件
【答案】A
【解析】解:∵𝑃:由𝑥2−4𝑥−5<0,解得:−1<𝑥<5,
q:由𝑥2+6𝑥+5>0,解得:𝑥>−1或𝑥<−5,
由𝑝⇒𝑞,而q推不出p,
∴𝑝是q的充分不必要条件,
故选:A.
分别解出关于p,q的不等式的解集,从而判断出p,q的关系.
本题考查了充分必要条件,考查了解不等式问题,是一道基础题.
5. 函数𝑓(𝑥)=2𝑥𝑒𝑥+𝑒−𝑥的部分图象大致为( ) 第3页,共18页 A. B. C. D.
【答案】A
【解析】解:∵𝑓(−𝑥)=−2𝑥𝑒−𝑥+𝑒𝑥=−𝑓(𝑥),∴函数𝑓(𝑥)为奇函数,排除选项B和C,
当𝑥→+∞时,𝑒𝑥比x增长的快,∴𝑓(𝑥)→0,排除选项D,
故选:A.
先判断函数的奇偶性,再考虑𝑥→+∞时,𝑓(𝑥)的取值情况,即可作出选择.
本题考查函数的图象与性质,一般可从函数的单调性、奇偶性或特殊点处的函数值等方面着手思考,考查学生的逻辑推理能力和运算求解能力,属于基础题.
6. 如图,在矩形ABCD中,𝐴𝐵=1,𝐵𝐶=√3,沿BD将矩形ABCD折叠,连接AC,所得三棱锥𝐴−𝐵𝐶𝐷正视图和俯视图如图,则三棱锥𝐴−𝐵𝐶𝐷中AC长为( )
A. 32 B. √3 C. √102 D. 2
【答案】C
【解析】解:根据矩形的折叠,得到:平面𝐴𝐵𝐷⊥平面BCD.
如图所示: 第4页,共18页
在平面ABD中,作𝐴𝐸⊥𝐷𝐵,在平面BCD中,作𝐶𝐹⊥𝐵𝐷,
利用射影定理:𝐴𝐵=1,𝐵𝐶=√3,
所以𝐵𝐷=2,
𝐴𝐵2=𝐵𝐸⋅𝐵𝐷,解得𝐵𝐸=12,
同理:𝐷𝐹=12,
所以𝐸𝐹=2−12−12=1,
则:𝐴𝐸2=𝐵𝐸⋅𝐸𝐷=12×32=34,
同理:𝐶𝐹2=34
所以|𝐴𝐶⃗⃗⃗⃗⃗ |2=|𝐴𝐸⃗⃗⃗⃗⃗ +𝐸𝐹⃗⃗⃗⃗⃗ +𝐹𝐶⃗⃗⃗⃗⃗ |2=|𝐴𝐸⃗⃗⃗⃗⃗ |2+|𝐸𝐹⃗⃗⃗⃗⃗ |2+|𝐹𝐶⃗⃗⃗⃗⃗ |2+2𝐴𝐸⃗⃗⃗⃗⃗ ⋅𝐸𝐹⃗⃗⃗⃗⃗ +2𝐸𝐹⃗⃗⃗⃗⃗ ⋅𝐹𝐶⃗⃗⃗⃗⃗ +2𝐴𝐸⃗⃗⃗⃗⃗ ⋅𝐹𝐶⃗⃗⃗⃗⃗ =34+34+1=104.
故AC=√102.
故选:C.
直接利用矩形的折叠的应用和射影定理,线面垂直的应用,勾股定理,向量的线性运算,向量的模的应用求出结果.
本题考查的知识要点:射影定理,线面垂直的应用,勾股定理,向量的线性运算,向量的模,主要考查学生的运算能力和转换能力及思维能力,属于基础题.
7. 已知直线l过第一象限的点(𝑚,𝑛)和(1,5),直线l的倾斜角为135°,则1𝑚+4𝑛的最小值为( )
A. 4 B. 9 C. 23 D. 32
【答案】D
【解析】解:根据题意,直线l过第一象限的点(𝑚,𝑛)和(1,5),直线l的倾斜角为135°,
则𝑛−5𝑚−1=−1,变形可得𝑚+𝑛=6,
则1𝑚+4𝑛=16×(1𝑚+4𝑛)(𝑚+𝑛)=16(5+4𝑚𝑛+𝑛𝑚), 第5页,共18页 又由点(𝑚,𝑛)在第一象限,即𝑚>0,𝑛>0,
则有4𝑚𝑛+𝑛𝑚≥2√4𝑚𝑛×𝑛𝑚=4,当且仅当𝑛=2𝑚时等号成立,
故1𝑚+4𝑛=16(5+4𝑚𝑛+𝑛𝑚)≥32,即1𝑚+4𝑛的最小值为32,
故选:D.
根据题意,由直线的斜率计算公式可得𝑛−5𝑚−1=−1,变形可得𝑚+𝑛=6,则有1𝑚+4𝑛=16×(1𝑚+4𝑛)(𝑚+𝑛)=16(5+4𝑚𝑛+𝑛𝑚),结合基本不等式的性质分析可得答案.
本题考查基本不等式的性质以及应用,涉及直线的斜率,属于基础题.
8. 设0<𝑎<13,随机变量𝜉的分布列为
𝜉 0 1 2
P a 1−3𝑎 2a
那么,当a在(0,13)内增大时,𝐷(𝜉)的变化是( )
A. 减小 B. 增大 C. 先减小后增大 D. 先增大后减小
【答案】B
【解析】解:由随机变量𝜉的分布列,得:
𝐸(𝜉)=1×(1−3𝑎)+2×2𝑎=1+𝑎,
𝐸(𝜉2)=1×(1−3𝑎)+4×2𝑎=1+5𝑎,
𝐷(𝜉)=𝐸(𝜉2)−𝐸2(𝜉)=(1+5𝑎)−(1+𝑎)2=−(𝑎−32)2+94,
当0<𝑎<13时,𝐷(𝜉)单调递增.
故选:B.
先求出𝐸(𝜉)=1+𝑎,𝐸(𝜉2)=1+5𝑎,再求出𝐷(𝜉)=𝐸(𝜉2)−𝐸2(𝜉)=(1+5𝑎)−(1+𝑎)2=−(𝑎−32)2+94,从而得到当0<𝑎<13时,𝐷(𝜉)单调递增.
本题考查离散型随机变量的方差的变化趋势的判断,涉及到离散型随机变量的分布列的性质等基础知识,考查运算求解能力等数学核心素养,是基础题.
9. 如图,在△𝐴𝐵𝐶中,𝐴𝐵=1,𝐵𝐶=2√2,𝐵=𝜋4,将△𝐴𝐵𝐶绕边AB翻转至△𝐴𝐵𝑃,使平面𝐴𝐵𝑃⊥平面ABC,D是第6页,共18页 BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ等于( )
A.
√52 B. 3√55
C. 2√55
D. 2√53
【答案】C
【解析】
【分析】
本题考查空间向量法在立体几何中的应用,考查利用向量法求线段长与直线所成的角,还考查利用导数研究函数的最值,考查运算求解能力,是中档题.
根据题意过点P作𝑃𝑂⊥平面ABC,交BA延长线于点O,连结OC,以O为原点,OB为x轴,OC为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出PC与DQ所成角的余弦值,再结合导数即可求得PC与DQ所成角取得最小值时,线段AQ的长.
【解答】
解:因为平面𝐴𝐵𝑃⊥平面ABC,交线为AB,
故过点P作𝑃𝑂⊥平面ABC,交BA延长线于点O,连结OC,
以O为原点,OB为x轴,OC为y轴,OP为z轴,建立空间直角坐标系,如图,
在△𝐴𝐵𝐶中,𝐴𝐵=1,𝐵𝐶=2√2,𝐵=𝜋4,
将△𝐴𝐵𝐶绕边AB翻转至△𝐴𝐵𝑃,
使平面𝐴𝐵𝑃⊥平面ABC,D是BC的中点,设Q是线段PA上的动点,
则𝐵(2,0,0),𝐴(1,0,0),𝑂(0,0,0),𝐶(0,2,0),𝑃(0,0,2), 第7页,共18页 设𝑄(𝑥,y,𝑧),𝐴𝑄⃗⃗⃗⃗⃗ =𝜆𝐴𝑃⃗⃗⃗⃗⃗ =𝜆(−1,0,2),𝜆∈[0,1],
即(𝑥−1,y,𝑧)=(−𝜆,0,2𝜆),∴𝑄(1−𝜆,0,2𝜆),
又D是BC的中点,故D(1,1,0),
𝐷𝑄⃗⃗⃗⃗⃗⃗ =(−𝜆,−1,2𝜆),𝑃𝐶⃗⃗⃗⃗⃗ =(0,2,−2),
|cos<𝐷𝑄⃗⃗⃗⃗⃗⃗ ,𝑃𝐶⃗⃗⃗⃗⃗ >|=|−2−4𝜆|√5𝜆2+1⋅2√2=1√2⋅√(1+2𝜆)25𝜆2+1,
令𝑓(𝜆)=(1+2𝜆)25𝜆2+1,𝜆∈[0,1],
∴𝑓′(𝜆)=2(1+2𝜆)(2−5𝜆)(5𝜆2+1)2,
由𝑓′(𝜆)=0,𝜆∈[0,1],得𝜆=25,
𝜆∈[0,25)时,𝑓′(𝜆)>0,𝜆∈(25,1]时,𝑓′(𝑥)<0,
∴当𝜆=25时,𝑓(𝜆)取最大值,此时PC与DQ所成角取得最小值,
|𝐴𝑄|=25|𝐴𝑃⃗⃗⃗⃗⃗ |=25√5.
故选:C.
10. 已知数列{𝑎𝑛}满足𝑎1=1,𝑎𝑛+1−𝑎𝑛>1𝑛+1(𝑛∈𝑁∗),则一定成立的是( )
A. 𝑎100>𝑙𝑛102 B. 𝑎99>𝑙𝑛100 C. 𝑎99<𝑙𝑛100 D. 𝑎100<𝑙𝑛99
【答案】B
【解析】解:∵𝑎1=1,𝑎𝑛+1−𝑎𝑛>1𝑛+1(𝑛∈𝑁∗),
∴𝑎𝑛−𝑎𝑛−1>1𝑛,𝑎𝑛−1−𝑎𝑛−2>1𝑛−1,…,𝑎2−𝑎1>12,
将上面的式子相加得到:𝑎𝑛−𝑎1>12+13+⋯+1𝑛(𝑛≥2),即𝑎𝑛>1+12+13+⋯+1𝑛,𝑛≥2,
令𝑓(𝑥)=ln(𝑥+1)−𝑥(𝑥>−1),当𝑥>0时,𝑓′(𝑥)=1𝑥+1−1<0,故当𝑥>0时,𝑓(𝑥)<𝑓(0)=0,即ln(𝑥+1)<𝑥,
∴ln𝑛+1𝑛=ln(1+1𝑛)<1𝑛,又ln(𝑛+1)=ln𝑛+1𝑛+ln𝑛𝑛−1+⋯+ln21,
∴𝑎𝑛>1+12+13+⋯+1𝑛>𝑙𝑛2+ln(1+12)+ln(1+13)+⋯+ln(1+1𝑛)=ln(𝑛+1),即𝑎𝑛>ln(𝑛+1),𝑛≥2,
∴𝑎99>𝑙𝑛100,
故选:B.