第五章分式与分式方程知识点总结

分式的相关知识点总结一、分式的定义和性质1. 分式的定义分式是指两个整数或者两个代数式的比值的表示形式.一般为 a/b 的形式，其中 a 和 b 都是整数，b 不等于 0。

2. 分式的性质(1) 分式的分子和分母互质：如果分数 a/b 已经约分为最简分数，那么 a 和 b 一定是互质的，即它们的最大公因数是 1。

(2) 分母为 1 的分数：如果分数的分母为 1，那就是一个整数，可以简单地把它看作一个整数。

(3) 分式的相等：分数 a/b 和 c/d 相等，当且仅当 ad = bc。

两个分式相等时，它们表示的比值是相等的。

二、分式的运算1. 分式的加法和减法(1) 加法和减法的分母变换：对于不同分母的分数，需要将它们的分母变为相同的数，然后再进行加法或减法运算。

(2) 加法和减法的运算规则：对于相同的分母，直接将分子相加或相减，分母保持不变。

2. 分式的乘法和除法(1) 乘法法则：两个分式相乘时，分子与分子相乘，分母与分母相乘，即 (a/b) * (c/d) = (a*c)/(b*d)。

(2) 除法法则：两个分式相除时，分子与分母相乘，分母与分子相乘，即 (a/b) / (c/d) = (a*d)/(b*c)。

三、分式的化简1. 分式的约分分式约分是指将分子与分母的公因数约掉，使其成为最简分式.一般采用求最大公因数的方法进行约分。

2. 分式的通分不同分母的分数，通分是指将它们的分母都变为相同的数，通常采用最小公倍数的方法进行通分。

3. 分式的化简原则(1) 分式中的公因式可以约掉；(2) 同等分母的分式相加或相减时，只需对各分子分别进行加减。

四、分式的应用1. 代数方程中的应用在解代数方程时，常常会遇到分式方程，需要对其进行分式的加减乘除，并化简以便求解。

2. 几何问题中的应用在几何中，常常会涉及到对分式的加减乘除和化简操作，特别是在比例、相似三角形、面积等方面的计算中。

3. 物理问题中的应用在物理中，分式广泛应用于密度、速度、功率等问题的计算中，需要进行分式的加减乘除以及化简操作。

第五章分式与知识点在数学的广袤天地中，分式是一个重要且有趣的概念。

它就像一座桥梁，连接着代数运算和实际问题，为我们解决各种数学难题提供了有力的工具。

分式，简单来说，就是形如 A/B 的式子，其中 A 和 B 都是整式，且 B 中含有字母。

这里要注意哦，分母 B 不能为零，否则这个式子就没有意义啦。

我们先来聊聊分式的基本性质。

它和分数的基本性质类似，分式的分子和分母同时乘以（或除以）同一个不为零的整式，分式的值不变。

这一性质可是分式运算的重要基础呢！比如，我们要对分式进行化简，就经常会用到它。

比如说，给定一个分式（2x)／（4x²) ，我们可以根据分式的基本性质，将分子分母同时除以2x ，得到1/（2x) ，这样就把分式化简了。

再来说说分式的约分和通分。

约分就是把分式的分子和分母中的公因式约去，让分式变得更简洁。

通分呢，则是把几个异分母的分式化为同分母的分式，方便进行加减运算。

举个例子，对于分式（x² 1)／（x ＋ 1) ，我们可以因式分解分子为（x ＋ 1)（x 1) ，然后约去分子分母的公因式（x ＋ 1) ，得到 x 1 。

而如果要计算（1/2x) ＋（1/3x) ，就需要先通分，找到 2x 和 3x 的最小公倍数 6x ，将两个分式分别化为（3/6x) 和（2/6x) ，然后相加得到 5/6x 。

分式的乘除运算也是重要的一部分。

分式乘以分式，用分子的积做积的分子，分母的积做积的分母；分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘。

例如，计算（2x/y) ×（3y/4x²) ，分子相乘得到 6xy ，分母相乘得到 4x²y ，约分后得到 3/（2x) 。

对于分式的加减运算，同分母的分式相加减，分母不变，把分子相加减；异分母的分式相加减，先通分，变为同分母的分式，再加减。

比如说，（2/x) ＋（3/x) ＝（5/x) ，而（1/x) （1/2x) ＝（2/2x) （1/2x) ＝ 1/2x 。

第五章分式与分式方程知识点1：分式的概念1、分式的定义：一般地，用A,B表示两个正式，A÷B可以表示成AB的形式。

如果B中含有字母，那么称AB为分式，其中A称为分式的分子，B称为分式的分母。

分式需要满足的三个条件：（1）是形如AB的式子；（2）A,B都整式；（3）分母B中必须含有字母。

分式有意义的条件：分母不能为0.分式无意义的条件：分母等于0.分式的值为0的条件：分子等于0且分母不等于0.知识点2：分式的性质2、分式的基本性质分式的基本性质：分式的分子与分母都乘（或除以）同一个不等于零的整式，分式的值不变。

字母表示：AB =A·CB·C，AB=A÷CB÷C(C≠0，其中A,B,C均是整式)运用条件：（1）分子和分母要同时做“乘法（或除法）”运算；（2）“乘（或除以）”的对象必须是同一个不等于0的整式。

3、分式的符号法则法则内容：分式的分子、分母与分式本身的符号同时改变其中两个，分式的值不变。

字母表示：AB =−A−B=−−AB=−A−B知识点3：分式的约分与通分4、分式的约分约分：根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分式的约分，即A·CB·C =AB（C为整式且C≠0）.约分的方法：如果分式的分子、分母都是单项式，那么直接约去分子、分母的公因式；如果分式的分子、分母中至少有一个多项式，那么先分解因式，再约去分子、分母的公因式。

最简分式：分子与分母没有公因式的分式，叫做最简分式。

5、分式的通分通分：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分。

用字母表示：将AB 和CD通分，AB=A·DB·D，CD=B·CB·D（分母都为B·D）。

通分的步骤：（1）将所有分式的分母化为乘积的形式，当分母为多项式时，应进行因式分解；（2）确定最简公分母，即各分母的所有因式的最高次幂的积；（3）将分子、分母同乘一个因式，使分母变为最简公分母。

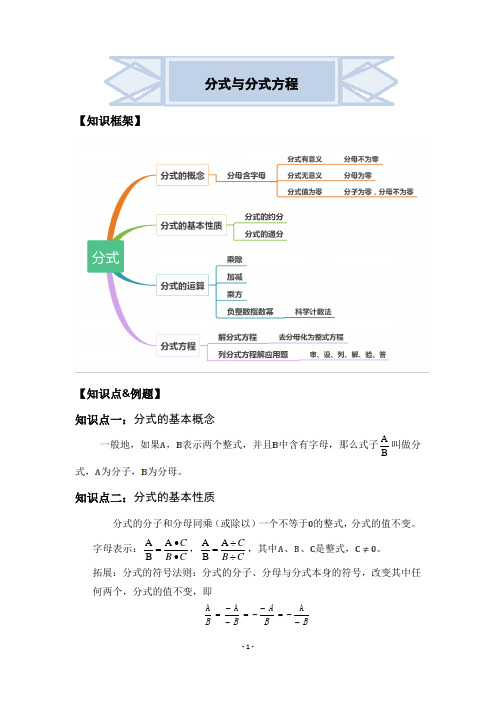
分式与分式方程【知识框架】【知识点&例题】知识点一：分式的基本概念一般地，如果，表示两个整式，并且中含有字母，那么式子B A 叫做分式，为分子，为分母。

知识点二：分式的基本性质 分式的分子和分母同乘（或除以）一个不等于的整式，分式的值不变。

字母表示：C B C••=A B A，C B C÷÷=A B A ，其中、、是整式，。

拓展：分式的符号法则：分式的分子、分母与分式本身的符号，改变其中任何两个，分式的值不变，即B B AB B --=--=--=AAA注意：在应用分式的基本性质时，要注意这个限制条件和隐含条件B ≠0。

知识点三：分式的乘除法法则分式乘分式：用分子的积作为积的分子，分母的积作为积的分母。

式子表示为：db c a d c b a ••=•分式除以分式：把除式的分子、分母颠倒位置后，与被除式相乘。

式子表示为cc ••=•=÷bd a d b a d c b a 分式的乘方：把分子、分母分别乘方。

式子n n nb a b a =⎪⎭⎫ ⎝⎛巩固练习：1.若分式的值为0，则x 的值为 .2.当= 时，分式的值为零.3.计算x xy y xy y xy y x xy y22222222++-÷+-+4.先化简，再求值：其中.242x x --x 26(1)(3)x x x x ----2291333x x x x x ⎛⎫-⋅ ⎪--+⎝⎭13x =5.先化简，再求值：，其中．6、先化简，再求值：，其中7、解下列方程：（1）（2）（3） （4）532224x x x x -⎛⎫--÷ ⎪++⎝⎭3x 22144(1)1a a a a a-+-÷--1a =-3522x x =-223444x x x x =--+22093x x x +=-+35012x x -=+9、在年春运期间，我国南方出现大范围冰雪灾害，导致某地电路断电.该地供电局组织电工进行抢修.供电局距离抢修工地千米.抢修车装载着所需材料先从供电局出发，分钟后，电工乘吉普车从同一地点出发，结果他们同时到达抢修工地．已知吉普车速度是抢修车速度的倍，求这两种车的速度。

分式与分式方程知识点一、分式的定义1. 分式（Fraction）：形如 A/B 的代数表达式，其中 A 是分子，B 是分母，B ≠ 0。

2. 有理表达式（Rational Expression）：包含分式的代数表达式。

二、分式的基本性质1. 等值变换：分式可以通过乘以或除以相同的非零表达式进行等值变换。

例如：(2/3) * (4/5) = (2*4)/(3*5) = 8/152. 分式的加减法：只有当分母相同时，才能直接进行加减运算。

例如：(2/5) + (3/5) = (2+3)/5 = 5/5 = 13. 分式的乘除法：分子乘分子，分母乘分母。

例如：(2/3) * (4/5) = (2*4)/(3*5) = 8/154. 分式的化简：通过约分，将分子和分母中的公因数相除，得到最简分式。

例如：(12/16) -> (12÷4)/(16÷4) = 3/4三、分式方程1. 分式方程（Fractional Equation）：含有分式的方程。

2. 解分式方程的基本原则：将分式方程转化为整式方程进行求解。

3. 去分母：通过将方程两边同时乘以所有分母的最简公分母，消除分母。

例如：(2/x) + (3/y) = 5 => 2y + 3x = 5xy (假设 x, y > 0) 4. 检验解：将求得的整式解代入最简公分母中，确保不会得到零。

四、特殊类型的分式方程1. 一元一次分式方程：只含有一个未知数，且未知数的最高次数为一的分式方程。

2. 二元一次分式方程：含有两个未知数，且每个未知数的最高次数为一的分式方程。

3. 高次分式方程：含有未知数的最高次数大于一的分式方程。

五、解分式方程的步骤1. 确定最简公分母。

2. 去分母，将分式方程转化为整式方程。

3. 解整式方程，求得未知数的值。

4. 检验解的有效性。

5. 写出最终解。

六、应用题1. 理解题意，找出等量关系。

2. 列出分式方程。

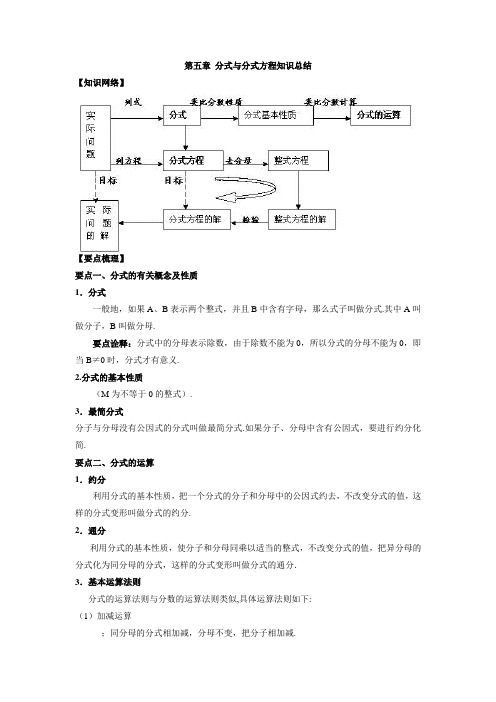
第五章分式与分式方程知识总结【知识网络】【要点梳理】要点一、分式的有关概念及性质1．分式一般地，如果A、B表示两个整式，并且B中含有字母，那么式子叫做分式.其中A叫做分子，B叫做分母.要点诠释：分式中的分母表示除数，由于除数不能为0，所以分式的分母不能为0，即当B≠0时，分式才有意义.2.分式的基本性质（M为不等于0的整式）.3．最简分式分子与分母没有公因式的分式叫做最简分式.如果分子、分母中含有公因式，要进行约分化简.要点二、分式的运算1．约分利用分式的基本性质，把一个分式的分子和分母中的公因式约去，不改变分式的值，这样的分式变形叫做分式的约分.2．通分利用分式的基本性质，使分子和分母同乘以适当的整式，不改变分式的值，把异分母的分式化为同分母的分式，这样的分式变形叫做分式的通分．3．基本运算法则分式的运算法则与分数的运算法则类似,具体运算法则如下:（1）加减运算；同分母的分式相加减，分母不变，把分子相加减.；异分母的分式相加减，先通分，变为同分母的分式，再加减.（2）乘法运算，其中是整式，.两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母.（3）除法运算，其中是整式，.两个分式相除，把除式的分子和分母颠倒位置后，与被除式相乘.（4）乘方运算分式的乘方，把分子、分母分别乘方.4.分式的混合运算顺序先算乘方，再算乘除，最后加减，有括号先算括号里面的.要点三、分式方程1．分式方程的概念分母中含有未知数的方程叫做分式方程．2．分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程．3．分式方程的增根问题增根的产生：分式方程本身隐含着分母不为0的条件，当把分式方程转化为整式方程后，方程中未知数允许取值的范围扩大了，如果转化后的整式方程的根恰好使原方程中分母的值为0，那么就会出现不适合原方程的根---增根.要点诠释：因为解分式方程可能出现增根，所以解分式方程必须验根．验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解.要点四、分式方程的应用列分式方程解应用题与列一元一次方程解应用题类似，但要稍复杂一些．解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节，从而正确列出方程，并进行求解.。

第五章 分式与分式方程1. 分式的定义：如果A 、B 表示两个整式，并且B 中含有字母，那么式子BA 叫做分式。

1) 分式与整式最本质的区别：分式的字母必须含有字母，即未知数；分子可含字母可不含字母。

2) 分式有意义的条件：分母不为零，即分母中的代数式的值不能为零。

3) 分式的值为零的条件：分子为零且分母不为零2. 分式的基本性质：分式的分子与分母同乘或除以一个不等于0的整式，分式的值不变。

用式子表示 或 其中A 、B 、C 为整式（0≠C ）注：（1）利用分式的基本性质进行分时变形是恒等变形，不改变分式值的大小，只改变形式。

（2）应用基本性质时，要注意C ≠0，以及隐含的B ≠0。

（3）注意“都”，分子分母要同时乘以或除以，避免只乘或只除以分子或分母的部分项，或避免出现分子、分母乘除的不是同一个整式的错误。

3. 分式的通分和约分：关键先是分解因式1) 分式的约分定义：利用分式的基本性质，约去分式的分子与分母的公因式，不改变分式的值。

2) 最简分式：分子与分母没有公因式的分式3) 分式的通分的定义：利用分式的基本性质，使分子和分母同乘适当的整式，不改变分式的值，把几个异分母的分式化成分母相同的分式。

4) 最简公分母：取“各个分母”的“所有因式”的最高次幂的积做公分母，它叫做最简公分母。

4. 分式的符号法则 C B C A B A ⋅⋅=CB C A B A ÷÷=分式的分子、分母与分式本身的符号，改变其中任何两个分式的值不变。

用式子表示为 注：分子与分母变号时，是指整个分子或分母同时变号，而不是指改变分子或分母中的部分项的符号。

5.分式的运算：1）分式乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为分母。

2）分式除法法则：分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘。

3）分式乘方法则： 分式乘方要把分子、分母分别乘方。

4）分式乘方、乘除混合运算：先算乘方，再算乘除，遇到括号，先算括号内的，不含括号的，按从左到右的顺序运算5）分式的加减法则：同分母的分式相加减，分母不变，把分子相加减。

第五章：分式与分式方程5.1认识分式一般地，用,A B 表示两个整式，A B ÷可以表示成A B 的形式，如果B 中含有字母，那么称A B为分式，其中A 称为分式的分子，B 称为分式的分母，对于任意一个分式，分母都不能为零.例1， 下列各式中哪些是整式？哪些是分式？211(1);;(3);(4);2242b a b x xy x y a x ++-+- (2) 分式的基本性质 分式的分子与分母都乘（或除以）同一个不等于零的整式，分式的值保持不变. 这一性质可以用式子表示为：,(0)b b m b b m m a a m a a m⋅÷==≠⋅÷. 把一个分式的分子和分母的公因式约去，这种变形称为分式的约分.例2， 化简下列分式 2225(1);;20xy a ab x y b ab++ (2) 在化简的结果中，如果分子和分母已没有公因式，这样的分式称为最简分式，化简分式时，通常要使结果成为最简分式或是整式.5.2分式的乘除法两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母；两个分式相除，把除式的分子和分母颠倒位置后在与被除式相乘. 这一法则可以用式子表示为：;b d bd b d b c bc a c ac a c a d ad⋅=÷=⋅= . 例3， 计算2222244(1);(4);2x xy xy x xy y x y x y x y x y+-+÷÷---+ (2) 5.3分式的加减法同分母的分式相加减，分母不变，把分子相加减. 这一法则可以用式子表示为：b c b c a a a±±=. 例4，计算222(1);(2);(3);22a b x y m n n n a b b a x y y x n m n m n m++++-------- 根据分式的基本性质，异分母的分式可以化为同分母的分式，这一过程称为分式的通分，为了计算方便，异分母分式通分时，通常取最简单的公分母（最简公分母）作为它们的共同分母.异分母分式的加减法法则是：异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法法则进行计算. 这一法则可以用式子表示为：;b d bc ad bc ad a c ac ac ac±±=±= 例5，计算22111(1);(2);(3);423332a b a a a x x a b--+---+ 5.4分式方程分母中含有未知数的方程叫做分式方程.因为解分式方程可能产生增根，所以解分式方程必须检验.通常只需检验所得的根是否使原方程中分式的分母的值等于零就好了，如果使原方程中分式的分母的值等于零，则舍去此根.例7， 解方程 653121(1);(2)1;(3)2;1(1)4433x x y x x x x x y y+--=+==-++---- 。

15.3分式方程一、本节学习指导解分式方程和我们前面学习的解方程有很多相似之处，期间会运用到很多分式的计算方式，就这一节来说并不难。

做适当练习即能掌握。

二、知识要点1、分式方程：含分式，并且分母中含未知数的方程叫做分式方程。

（1）、分式方程的解法：解分式方程的基本思想方法是：分式方程转化去分母整式方程.解分式方程的一般方法和步骤：①去分母：即在方程的两边都同时乘以最简公分母，把分式方程化为整式方程，依据是等式的基本性质；②解这个整式方程；③检验：把整式方程的解代入最简公分母，使最简公分母不等于0的解是原方程的解，使最简公分母等于0的解不是原方程的解，即说明原分式方程无解。

注意：①去分母时，方程两边的每一项都乘以最简公分母，不要漏乘不含分母的项；②解分式方程必须要验根，千万不要忘了！（2）、解分式方程的步骤：(1)能化简的先化简；(2)方程两边同乘以最简公分母，化为整式方程；(3)解整式方程；(4)验根．（3）、分式方程检验方法：将整式方程的解带入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解。

（4）、含有字母的分式方程的解法：在数学式子的字母不仅可以表示未知数，也可以表示已知数，含有字母已知数的分式方程的解法，也是去分母，解整式方程，检验这三个步骤，需要注意的是要找准哪个字母表示未知数，哪个字母表示未知数，还要注意题目的限制条件。

计算结果是用已知数表示未知数，不要混淆。

2、列分式方程解应用题（1）列分式方程解应用题的步骤：①审：审清题意；②找: 找出相等关系；③设：设未知数；④列：列出分式方程；⑤解：解这个分式方程；⑥验：既要检验根是否是所列分式方程的解，又要检验根是否符合题意；⑦答：写出答案。

（2）应用题有几种类型；基本公式是什么？常见的有以下五种：①行程问题基本公式：路程=速度×时间而行程问题中又分相遇问题、追及问题．②数字问题：在数字问题中要掌握十进制数的表示法．③工程问题基本公式：工作量=工时×工效．④顺水逆水问题=+•=-v v v v v v顺水静水水逆水静水水3、科学记数法：把一个数表示成的形式10na⨯（其中≤a，n是整数）的记数方法叫做科学记数法．1<10（1）、用科学记数法表示绝对值大于1的数时，应当表示为10na⨯的形式,其中1≤︱a︱＜10,n为原整数部分的位数减1；（2）、用科学记数法表示绝对值小于1的数时,则可表示为10n⨯的形式，其中n为原数第1个不为0的a-数字前面所有0的个数(包括小数点前面的那个0)，1≤︱a︱＜10.三、经验之谈：这一节考点比较多的应该是分式方程的应用题和科学计数法，但应用题基本不会单独命题，步骤虽繁琐，但是难度并不大。

分式知识点归纳与总结分式是初中数学中的重要内容之一，它与整式一起构成了代数式的基础。

为了帮助大家更好地理解和掌握分式的相关知识，下面将对分式的知识点进行详细的归纳与总结。

一、分式的定义如果 A、B 表示两个整式，并且 B 中含有字母，那么式子 A/B 就叫做分式。

其中 A 叫做分子，B 叫做分母。

需要注意的是，分式的分母不能为 0，因为除数不能为 0。

如果分母 B 的值为 0，那么分式 A/B 就没有意义。

例如，x/（x ＋ 1) 是一个分式，因为分母 x ＋ 1 中含有字母 x；而2/3 不是分式，因为分母 3 是一个常数，不含有字母。

二、分式有意义、无意义和值为 0 的条件1、分式有意义的条件：分母不为 0。

即当B ≠ 0 时，分式 A/B 有意义。

例如，对于分式 1/（x 2)，要使其有意义，必须满足x 2 ≠ 0，即 x ≠ 2。

2、分式无意义的条件：分母为 0。

即当 B ＝ 0 时，分式 A/B 无意义。

例如，对于分式 3/（x ＋ 3)，当 x ＋ 3 ＝ 0，即 x ＝－3 时，分式无意义。

3、分式值为 0 的条件：分子为 0 且分母不为 0。

即当 A ＝ 0 且B ≠ 0 时，分式 A/B 的值为 0。

例如，对于分式（x 1)／（x ＋ 2)，要使其值为 0，必须满足 x 1＝ 0 且 x ＋2 ≠ 0，解得 x ＝ 1。

三、分式的基本性质分式的分子和分母同时乘以（或除以）同一个不为 0 的整式，分式的值不变。

用式子表示为：A/B ＝ A×C/B×C，A/B ＝ A÷C/B÷C（C 为不等于 0 的整式）例如，对于分式2x/（3y)，将分子分母同时乘以2，得到4x/（6y)，分式的值不变。

这个性质是分式化简和计算的重要依据。

四、分式的约分把一个分式的分子和分母的公因式约去，叫做分式的约分。

约分的关键是确定分子和分母的公因式。

公因式的确定方法：系数取分子和分母系数的最大公因数，字母取分子和分母共有的字母，相同字母取最低次幂。

知识点1、分式概念重点：掌握分式的概念和分式有意义的条件难点：分式有意义、分式值为0的条件 分式的概念：形如B A ，其中分母B 中含有字母，分数是整式而不是分式. (1)分式无意义时，分母中的字母的取值使分母为零，即当B=0时分式无意义.(2)求分式的值为零时，必须在分式有意义的前提下进行，分式的值为零要同时满足分母的值不为零及分子的值为零，这两个条件缺一不可.(3)分式有意义，就是分式里的分母的值不为零.易错易混点(1) 对分式的定义理解不准确；(2)不注意分式的值为零的条件；知识点2、分式的基本性质重点：正确理解分式的基本性质.难点：运用分式的基本性质，将分式约分、通分分式的基本性质：分式的分子与分母都乘以(或除以)同一个不等于零的整式，分式的值不变，用式子表示是：AB=MB M A ⨯⨯，AB=M B M A ÷÷.(其中M 是不等于零的整式)分式中的A ，B ，M 三个字母都表示整式，其中B 必须含有字母，除A 可等于零外，B ，M 都不能等于零.因为若B=0，分式无意义；若M=0，那么不论乘或除以分式的分母，都将使分式无意义.分式的约分和通分(1)约分的概念：把一个分式的分子与分母的公因式约去，叫做分式的约分．(2)分式约分的依据：分式的基本性质．(3)分式约分的方法：把分式的分子与分母分解因式，然后约去分子与分母的公因式．(4)最简分式的概念：一个分式的分子与分母没有公因式时，叫做最简分式．求几个分式的最简公分母的步骤：1．取各分式的分母中系数最小公倍数；2．各分式的分母中所有字母或因式都要取到；3．相同字母（或因式）的幂取指数最大的；4．所得的系数的最小公倍数与各字母（或因式）的最高次幂的积（其中系数都取正数）即为最简公分母。

各个分式的分母都是多项式，并且可以分解因式。

这时，可先把各分式的分母中的多项式分解因式，再确定各分式的最简公分母，最后通分。

易错易混点分式的分子、分母都是几个因式的积的形式，所以约去分子、分母中相同因式的最低次幂，注意系数也要约分。

分式与分式方程分式是数学中的一个重要概念，它由一个或多个整数构成的比的形式表示。

分式为我们解决很多实际问题提供了便利，特别是在代数方程的求解过程中，分式方程的出现频率相当高。

本文将介绍分式的基本概念、性质及其在解决分式方程中的应用。

一、分式的基本概念分式是一种特殊的比的表示形式，可以用“a/b”的形式表示，其中a 和b是整数，且b不等于0。

分式中，a被称为分子，b被称为分母。

分子表示被分割的部分，分母表示分割的份数。

例如，2/3就是一个分式，其中2是分子，3是分母。

这个分式表示将一个事物分成3个等份，取其中的2份。

二、分式的性质1. 基本性质：分式的值不仅依赖于分子和分母，还依赖于它们所表达的实际意义。

2. 约分：若分子和分母有公因数，可以约去这些公因数，使得分式更简洁。

3. 相等关系：分数相等的条件是分子与分子的乘积等于分母与分母的乘积。

4. 倒数性质：一个分式的倒数是将其分子与分母互换得到的分式。

三、分式的四则运算分式的四则运算包括加法、减法、乘法和除法。

下面分别介绍：1. 加法和减法：若两个分式的分母相同，就可以直接将它们的分子相加或相减，然后保持分母不变。

例如：(1/3) + (1/4) = (4/12) + (3/12) = 7/12(2/5) - (3/5) = (2/5) + (-3/5) = -1/5若两个分式的分母不同，则需要找到它们的最小公倍数来进行通分，再进行加减。

例如：(1/6) + (3/8) = (4/8) + (3/8) = 7/8(3/4) - (1/2) = (3/4) - (2/4) = 1/42. 乘法：两个分式相乘时，直接将它们的分子相乘，分母相乘。

例如：(2/3) * (3/5) = (2*3) / (3*5) = 6/153. 除法：两个分式相除时，将被除数与除数的倒数相乘。

例如：(2/3) ÷ (5/7) = (2/3) * (7/5) = 14/15四、分式方程的解法分式方程是含有一个或多个未知数的方程，其中包含分式。

第五章分式与分式方程复习总结第一课时知识点梳理肇州三中黄国庆教学目标1•将本章知识点形成知识脉络。

2. 培养学生如何建立完整的知识体系的能力。

教学重点1. 分式的概念及其基本性质。

2. 分式的运算法则。

3. 分式方程的概念、解法。

教学难点分式的运算及分式方程的解法.教学过程一、知识点梳理：1. 分式的定义：如果A B表示两个整式，并且B中含有字母，那么式子A叫做分式。

B1）分式与整式最本质的区别：分式的字母必须含有字母，即未知数；分子可含字母可不含字母2）分式有意义的条件：分母不为零，即坟墓中的代数式的值不能为零。

3）分式的值为零的条件：分子为零且分母不为零2. 分式的基本性质：分式的分子与分母同乘或除以一个不等于0的整式，分式的值不变。

用式子表示A^C I A-C其中A B、C为整式（C 0）B BC B B C注：（1）利用分式的基本性质进行分时变形是恒等变形，不改变分式值的大小，只改变形式。

（2）应用基本性质时，要注意C M0,以及隐含的B M0。

（3）注意“都”，分子分母要同时乘以或除以，避免只乘或只除以分子或分母的部分项，或避免出现分子、分母乘除的不是同一个整式的错误。

3. 分式的通分和约分：关键先是分解因式1）分式的约分定义：利用分式的基本性质，约去分式的分子与分母的公因式，不改变分式的值。

2）最简分式：分子与分母没有公因式的分式3）分式的通分的定义：利用分式的基本性质，使分子和分母同乘适当的整式，不改变分式的值，把几个异分母的分式化成分母相同的分式。

4）最简公分母：取“各个分母”的“所有因式”的最高次幕的积做公分母，它叫做最简公分母4. 分式的运算:1）分式乘法法则：分式乘分式，用分子的积作为积的分子，分母 的积作为分母。

2）分式除法法则：分式除以分式，把除式的分子、分母颠倒位置 后，与被除式相乘a c ac a c ad ad■b d bd b d be be3）分式的加减法则：同分母的分式相加减，分母不变，把分子相加减异分母的分式相加减，先通分，变为同分母分式，然后再加减a b a b a c ad be ad be c c c ，b d bd bd bd5. 分式方程：含分式，并且分母中含未知数的方程 分式方程。