(完整版)摄像机模型及坐标变换分解

相机标定的来龙去脉（详解标定原理、畸变矫正原理、使用经验）1、相机标定的意义在机器视觉领域，相机的标定是一个关键的环节，它决定了机器视觉系统能否有效的定位，能否有效的计算目标物。

相机的标定基本上可以分为两种，第一种是相机的自标定；第二种是依赖于标定参照物的标定方法。

前者是相机拍摄周围物体，通过数字图像处理的方法和相关的几何计算得到相机参数，但是这种方法标定的结果误差较大，不适合于高精度应用场合。

后者是通过标定参照物，由相机成像，并通过数字图像处理的方法，以及后期的空间算术运算计算相机的内参和外参。

这种方法标定的精度高，适用于对精度要求高的应用场合。

本文主要写一写后者，至于前者，是一个研究的难点和热点，以后有空再写。

2、坐标系的变换2.1、小孔成像的原理小孔成像的原理可以用下图来说明：2.2、各个坐标系的定义为了说明白，建议先介绍图像的坐标系，再逐步推广到世界坐标系，最后说明各个坐标系是如何变化的，从而给出相机的内参和外参。

2.2.1、像素坐标系像素坐标就是像素在图像中的位置。

一般像素坐标系的左上角的顶点就是远点，水平向右是u，垂直向下是v轴。

例如，在上图中，任意一个像素点的坐标可以表示为（ui,vi）。

2.2.2、图像坐标系在像素坐标系中，每个像素的坐标是用像素来表示的，然而，像素的表示方法却不能反应图像中物体的物力尺寸，因此，有必要将像素坐标转换为图像坐标。

将像素坐标系的原点平移到图像的中心，就定为图像坐标系的原点，图像坐标系的x轴与像素坐标系的u轴平行，方向相同，而图像坐标系的y轴与像素坐标系的v轴平行，方向相同。

在图中，假设图像中心的像素坐标是（u0,v0），相机中感光器件每个像素的物力尺寸是dx * dy，那么，图像坐标系的坐标（x,y）与像素坐标系的坐标（u,v）之间的关系可以表示为：写成矩阵的形式就为改写为齐次坐标的形式2.2.3、相机坐标系相机坐标系是以相机的光轴作为Z轴，光线在相机光学系统的中心位置就是原点Oc（实际上就是透镜的中心）,相机坐标系的水平轴Xc与垂直轴Yc分别于图像坐标系的X轴和Y轴平行。

相机坐标系与世界坐标系转换公式
相机坐标系与世界坐标系是计算机视觉和计算机图形学中重要的概念之一。

在三维场景中，相机坐标系是以相机为原点建立的坐标系，而世界坐标系是以场景中某一个固定点为原点建立的坐标系。

在进行三维物体的渲染和图像处理时，常常需要将相机坐标系中的坐标转换为世界坐标系中的坐标，或者将世界坐标系中的坐标转换为相机坐标系中的坐标。

以下是相机坐标系与世界坐标系转换公式：
1. 将世界坐标系中的点P(xw, yw, zw)转换为相机坐标系中的点Pc(xc, yc, zc)：
Pc = R * (P - T)
其中，R是旋转矩阵，T是平移向量，可以通过相机的位置和姿态计算得到。

2. 将相机坐标系中的点Pc(xc, yc, zc)转换为图像坐标系中的点Pp(u, v)：
Pp = (fu * xc / zc + cu, fv * yc / zc + cv)
其中，fu和fv是相机的焦距，cu和cv是相机的像素中心点，可以通过相机的内部参数矩阵计算得到。

3. 将图像坐标系中的点Pp(u, v)转换为像素坐标系中的点Ppix(x, y)：
Ppix = round(Pp)
其中，round表示四舍五入操作，将浮点数坐标转换为整数坐
标。

以上是相机坐标系与世界坐标系转换的基本公式，在实际应用中需要根据具体情况进行修正和优化。

数字图像处理中的变分模型与分割技术数字图像处理是一种广泛应用于计算机视觉、图像处理、图像分析等领域的技术。

其中的变分模型与分割技术是数字图像处理的重要组成部分，广泛应用于各种图像处理领域，如医学影像处理、物体识别、目标检测等。

变分模型是指对一个系统的能量函数进行最小化或最大化的过程，其中的能量函数是由图像像素的灰度值、空间距离和各种边缘等特征组成的。

常见的变分模型有全变分模型和TV（Total Variation）模型。

全变分模型是一种常见的图像处理方法，它可以将一个图像分解成多个层次，形成一个自适应的图像分割系统。

它可以有效地对图像进行边缘检测和分割。

TV模型则是一种基于局部均匀性假设的变分模型，它可以有效地管理图像分割中的噪声，并通过对图像的总变化量进行最小化来实现对图像分割的优化。

在分割技术中，边缘检测是关键环节之一。

边缘检测是指通过检测出图像中明显的边缘，进而将图像分割成若干区域的处理方法。

边缘检测技术包括Prewitt算子、Sobel算子、Canny算子等方法。

其中，Canny算法是一种基于高斯滤波、梯度计算、非极大值抑制和双阈值化等多项技术的综合算法，它可以有效地检测图像中的边缘，并将图像分割成多个区域。

除了边缘检测之外，聚类分析也是数字图像处理中广泛使用的分割技术之一。

聚类分析是指将具有相同特征的图像像素归为一类的过程。

它可以有效地将图像分割成多个相似的区域，常见的聚类算法有k-means算法、谱聚类算法等。

此外，分水岭算法也是一种常见的数字图像分割算法。

它是基于图像水平线的思想设计而成的一种聚类算法，可以将图像分割成多个区域，并在每个区域周围形成边缘。

分水岭算法广泛应用于医学影像处理中的肺部分割、乳腺分割等领域。

总之，数字图像处理中的变分模型与分割技术是数字图像处理的重要组成部分，可以有效地对图像进行边缘检测、目标分割、肿瘤检测等领域。

未来，随着计算机视觉和人工智能技术的不断发展，数字图像处理技术将在更多领域得到应用。

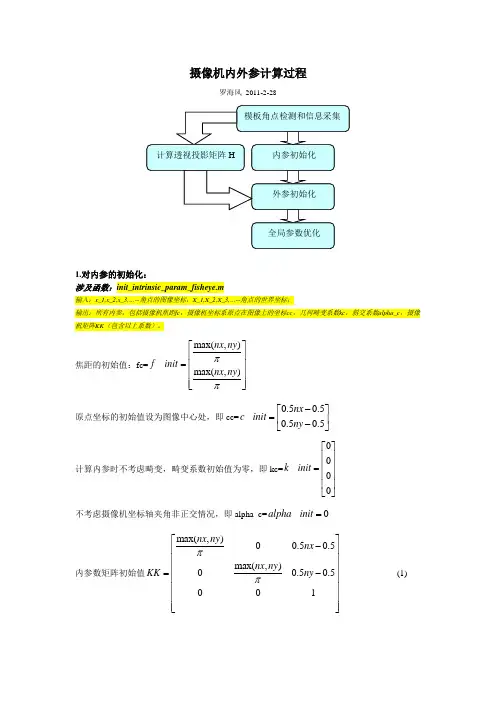
摄像机内外参计算过程罗海风2011-2-281.对内参的初始化：涉及函数：init_intrinsic_param_fisheye.m输入：x_1,x_2,x_3,…--角点的图像坐标，X_1,X_2,X_3,…--角点的世界坐标；输出：所有内参，包括摄像机焦距fc，摄像机坐标系原点在图像上的坐标cc，几何畸变系数kc，斜交系数alpha_c，摄像机矩阵KK（包含以上系数）。

焦距的初始值：fc=max(,)_max(,)nx nyf initnx nyππ⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦原点坐标的初始值设为图像中心处，即cc=0.50.5 _0.50.5nxc initny-⎡⎤=⎢⎥-⎣⎦计算内参时不考虑畸变，畸变系数初始值为零，即kc=0 _0 k init⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦不考虑摄像机坐标轴夹角非正交情况，即alpha_c=_0alpha init=内参数矩阵初始值max(,)00.50.5max(,)00.50.5001nx nynxnx nyKK nyππ⎡⎤-⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦-------------------(1)2.对外参的初始化：涉及函数：comp_ext_calib_fisheye.m功能：主要是调用compute_extrinsic_init_fisheye.m 和compute_extrinsic_refine_fisheye.mcompute_extrinsic_init_fisheye.m输入：像点的世界坐标和图像坐标x_kk 和X_kk,以及所有内参fc,cc,kc,alpha_c; 输出：所有外参初始值，包括平移矩阵Tckk ，旋转矩阵Rckk 和旋转向量omckkcompute_extrinsic_refine_fisheye.m输入：像点的世界坐标和图像坐标x_kk 和X_kk,最大迭代次数MaxIter 以及所有内参fc,cc,kc,alpha_c; 输出：所有外参初始值，包括平移矩阵Tckk ，旋转矩阵Rckk 和旋转向量omckk对像点世界坐标和图像坐标进行整理（整理过程考虑到坐标变换和畸变模型，涉及normalize_pixel_fisheye .m 输入：像点图像坐标x_kk,所有内参fc,cc,kc,alpha_c;输出：标准化无畸变图像坐标xn ）。

相机切向畸变模型1. 引言相机镜头的畸变是指由于镜头的物理结构和光学特性导致的图像形变现象。

其中，切向畸变是一种常见的畸变形式之一。

本文将对相机切向畸变模型进行推导和编写。

2. 相机切向畸变模型推导相机切向畸变模型是一种描述相机图像畸变的数学模型。

它假设相机的切向畸变主要由镜头的物理结构引起，并通过一组参数来描述畸变的程度。

2.1 坐标系首先，我们需要定义相机坐标系和图像坐标系。

相机坐标系是相机内部的坐标系，以相机光心为原点，相机光轴为Z轴正方向，X轴和Y轴分别与图像平面垂直。

图像坐标系以图像平面为基准，原点位于图像平面上的某个点。

2.2 相机内部参数相机内部参数是描述相机光学特性的参数，包括焦距、主点位置等。

在相机切向畸变模型中，我们主要关注焦距和主点位置两个参数。

2.3 相机切向畸变模型相机切向畸变模型假设图像上的每个像素点的坐标(x,y)在经过畸变后的坐标(x’,y’)可以通过以下公式计算得到：x’ = x + (2 * p1 * y + p2 * (r^2 + 2 * x^2)) y’ = y + (p1 * (r^2 + 2 * y^2) + 2 * p2 * x)其中，p1和p2是切向畸变的参数，r^2 = x^2 + y^2是像素点到光轴的距离的平方。

2.4 参数估计为了使用相机切向畸变模型对图像进行畸变校正，我们需要估计切向畸变的参数p1和p2。

常见的方法是使用标定板，通过观察标定板上的已知点在图像上的位置来估计这些参数。

3. 编写相机切向畸变模型代码import numpy as npdef undistort_image(image, p1, p2):# 获取图像尺寸height, width = image.shape[:2]# 计算图像中心点cx = width / 2cy = height / 2# 创建输出图像undistorted_image = np.zeros_like(image)# 遍历图像上的每个像素点for y in range(height):for x in range(width):# 计算像素点到光轴的距离r_squared = (x - cx)**2 + (y - cy)**2# 计算畸变校正后的坐标x_distorted = x + (2 * p1 * y + p2 * (r_squared + 2 * x**2))y_distorted = y + (p1 * (r_squared + 2 * y**2) + 2 * p2 * x)# 将校正后的像素点赋值给输出图像undistorted_image[y, x] = image[y_distorted, x_distorted] return undistorted_image# 调用undistort_image函数进行畸变校正undistorted_image = undistort_image(image, p1, p2)4. 结论相机切向畸变模型是一种常用的描述相机图像畸变的数学模型。

相机坐标系与世界坐标系转换公式
相机坐标系与世界坐标系是计算机图形学中常用的两个坐标系。

相机坐标系是相机本身的坐标系，原点为相机的位置，Z轴为相机的观察方向，X轴和Y轴分别为相机平面上的水平和竖直方向。

而世界坐标系是场景或物体所在的坐标系，原点可以是任意位置，三个坐标轴之间的角度也可以任意设置。

在计算机图形学中，通常需要将相机拍摄的图像转换到世界坐标系中，或是将世界坐标系中的物体投影到相机坐标系中。

为了实现这种转换，需要用到相机坐标系与世界坐标系之间的转换公式。

相机坐标系转换到世界坐标系的公式可以表示为：
P_w = R * P_c + t
其中，P_w表示在世界坐标系中的点坐标，P_c表示在相机坐标系中的点坐标，R表示相机坐标系到世界坐标系的旋转矩阵，t表示相机坐标系到世界坐标系的平移向量。

世界坐标系转换到相机坐标系的公式可以表示为：
P_c = R' * (P_w - t)
其中，P_w和P_c的含义同上，R'表示世界坐标系到相机坐标系的旋转矩阵的逆矩阵，即R的转置。

t同上。

以上就是相机坐标系与世界坐标系转换的公式，这些公式可以帮助我们在计算机图形学中进行相应的转换与计算。

- 1 -。

一、坐标系的定义（1）大地坐标系()c c c c Z Y X O C -WGS-84大地坐标系原点位于地球质心，c Z 轴指向地球北极，c X 轴由原点指向格林尼治平子午面与赤道交点，c Y 轴垂直c c c Z O X 平面与c Z 轴，c X 轴共同组成右手坐标系称为大地坐标系。

某点大地坐标系下坐标用()H L B ,,表示，分别表示该点的经度、纬度和大地高程。

（2）空间大地直角坐标系()g g g g Z Y X O G -空间大地直角坐标系具有与大地坐标系相同的坐标轴。

不同的是，空间大地直角坐标系为笛卡尔坐标系，大地坐标系为椭球坐标系。

某点的大地直角坐标系下的坐标用()gg g z y x ,,表示。

（3）地理坐标系()s s s s Z Y X O S -以无人机平台为例，将无人机平台看做质点，飞机平台的位置()H L B ,,即为地理坐标系的原点，可以表示为()s s s h ,,αλ，s Z 轴指向正北方向，s X 轴由原点指向天顶方向，s Y 与s Z 和s X 组合起来构成右手坐标系被称为地理坐标系。

该坐标系也为笛卡尔坐标系。

某点地理坐标系下坐标用()s s s z y x ,,表示。

（4）无人机坐标系()a a a a Z Y X O A -无人机坐标系和地理坐标系具有相同的原点。

无人机坐标系相当于地理坐标系经过三轴旋转而成的坐标系，当无人机姿态角均为零时，无人机坐标系与地理坐标系重合。

设无人机三轴姿态角为λκθ，，，无人机坐标系即为地理坐标系绕a Y （俯仰），a Z （横滚），a X （偏航）旋转λκθ，，后形成的坐标系。

某点载机坐标系下坐标用()a a a z y x ,,表示。

（5）摄像机坐标系()t t t t Z Y X O T -质点位于摄像机光轴与摄像机镜头平面的交点，t Z 轴定义为指向目标物体时摄像机光轴的方向，当t Z 轴处于水平方向时，t X 轴指向天顶方向，t Y 轴与t Z 轴和t X 轴共同组成的右手坐标系称为摄像机坐标系。

两种七参数坐标转换模型的坐标转换精度分析目录1. 内容概括 (2)1.1 研究背景 (3)1.2 研究意义 (3)1.3 国内外研究概况 (5)1.4 本文研究内容与方法 (6)2. 两种七参数坐标转换模型 (7)2.1 七参数坐标转换模型简介 (8)2.1.1 模型的基本原理 (9)2.1.2 模型的参数定义 (10)2.2 两种七参数坐标转换模型的比较 (11)2.2.1 模型特性的比较 (12)2.2.2 模型适用条件 (13)3. 坐标转换精度分析方法 (14)3.1 精度分析的目的与要求 (15)3.2 精度分析的方法与工具 (16)3.3 精度分析的评估指标 (18)4. 精度分析实验设计 (19)4.1 实验数据来源 (20)4.2 实验数据的处理 (21)4.3 实验方案与参数设置 (22)5. 两种七参数坐标转换模型的精度分析 (23)5.1 模型A的精度分析 (24)5.1.1 实验结果 (25)5.1.2 分析与讨论 (26)5.2 模型B的精度分析 (28)5.2.1 实验结果 (29)5.2.2 分析与讨论 (31)5.3 两种模型性能对比 (32)1. 内容概括本研究旨在探讨并分析两种不同的七参数坐标转换模型的坐标转换精度。

这两种模型广泛应用于地理信息系统（GIS）和地球科学领域，用于实现不同坐标系统之间的转换。

七参数模型相较于传统的六参数模型多了一个椭球离心率参数，这使得模型在转换过程中能够更好地捕捉和处理地球曲率的影响，因此在高精度定位和地图投影转换中尤为重要。

分析将包括理论推导和数值模拟两部分，理论推导将详细描述两种模型的数学原理和参数意义，为后续的分析提供理论支持。

数值模拟则通过实际数据和对地理空间数据的模拟，对两种模型的坐标转换精度进行量化评估。

我们将通过计算模型转换结果与真实值之间的偏差、残差和相关统计量，比较两种模型的性能，并探讨哪种模型更能准确满足不同的坐标转换需求。

一种倾斜摄影实景三维模型的空间坐标系统转换方法本文提出了一种新的的倾斜摄影实景三维模型的空间坐标系统转换方法，旨在提高倾斜摄影实景三维模型中的空间坐标系的精度和准确性。

本文首先介绍了倾斜摄影实景三维模型的基本概念，然后介绍了本方法的实现流程和核心算法，最后通过实验验证了本方法的有效性。

倾斜摄影实景三维模型是一种通过采集真实场景的倾斜摄影影像数据，并利用三维重建技术生成的三维模型。

由于摄影影像数据通常包含多个角度和位置拍摄的影像，因此倾斜摄影实景三维模型包含了丰富的空间信息和几何特征。

在实际应用中，倾斜摄影实景三维模型广泛用于城市规划、工程测量和建筑设计等领域。

在倾斜摄影实景三维模型中，空间坐标系统的转换是一个非常重要的问题。

传统的空间坐标系统转换方法通常采用高精度的全站仪或GPS等测量设备进行，但这些设备需要高昂的成本和复杂的操作，不利于实际应用。

因此，本文提出了一种基于图像匹配和控制点约束的空间坐标系统转换方法，可以利用倾斜摄影实景三维模型中的自然特征和控制点信息进行坐标转换，具有成本低、操作简单和精度高等优点。

本方法的实现流程如下：首先，在倾斜摄影实景三维模型中选取若干组控制点，其中至少一组控制点需具有已知坐标，通过三维重建技术在模型中标记出来。

然后，在影像数据中利用SIFT算法提取自然特征点，并利用RANSAC算法进行特征匹配和筛选，得到特征点匹配对。

接着，在特征点匹配对中筛选出与控制点匹配的对应特征点对，并通过二元线性方程组求解旋转矩阵、平移矢量和尺度因子，最终实现空间坐标系的转换。

本方法的核心算法即是旋转、平移和尺度的求解。

旋转矩阵R的求解可以通过选取三对匹配的特征点，按照对应的像素坐标和模型空间坐标进行线性重心变换，得到一个3×3的线性方程组，通过奇异值分解或QR分解求解得到旋转矩阵。

平移向量t的求解可以通过控制点的坐标和模型空间坐标的距离关系求解，即计算控制点在模型坐标系下的均值和影像坐标系下的均值之间的差值。

计算机视觉之相机成像原理：世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的转换本⽂链接：https:///chentravelling/article/details/535580960.前⾔最近整理了"相机成像原理"和"视差与深度信息"相关的资料，然后做成了PPT，以备⾃⼰⽤，也提供给相关的图像、视觉⽅向的朋友参考。

如有误，望海涵并指出。

1.正⽂图像处理、⽴体视觉等等⽅向常常涉及到四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。

例如下图：构建世界坐标系只是为了更好的描述相机的位置在哪⾥，在双⽬视觉中⼀般将世界坐标系原点定在左相机或者右相机或者⼆者X轴⽅向的中点。

接下来的重点，就是关于这⼏个坐标系的转换。

也就是说，⼀个现实中的物体是如何在图像中成像的。

1.1世界坐标系与相机坐标系于是，从世界坐标系到相机坐标系，涉及到旋转和平移（其实所有的运动也可以⽤旋转矩阵和平移向量来描述）。

绕着不同的坐标轴旋转不同的⾓度，得到相应的旋转矩阵，如下图所⽰：那么从世界坐标系到相机坐标系的转换关系如下所⽰：1.2相机坐标系与图像坐标系从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。

此时投影点p的单位还是mm，并不是pixel，需要进⼀步转换到像素坐标系。

1.3图像坐标系与像素坐标系像素坐标系和图像坐标系都在成像平⾯上，只是各⾃的原点和度量单位不⼀样。

图像坐标系的原点为相机光轴与成像平⾯的交点，通常情况下是成像平⾯的中点或者叫principal point。

图像坐标系的单位是mm，属于物理单位，⽽像素坐标系的单位是pixel，我们平常描述⼀个像素点都是⼏⾏⼏列。

所以这⼆者之间的转换如下：其中dx和dy表⽰每⼀列和每⼀⾏分别代表多少mm，即1pixel=dx mm那么通过上⾯四个坐标系的转换就可以得到⼀个点从世界坐标系如何转换到像素坐标系的。

其中相机的内参和外参可以通过张正友标定获取（戳）。

摄影测量学第一章绪论1、摄影测量是从非接触成像系统，经过记录、量测、解析与表达等办理，获取地球及其环境和其他物体的几何、属性等可靠信息的工艺、科学与技术。

2、摄影测量学的三个睁开阶段：模拟摄影测量、解析摄影测量、数字摄影测量3、摄影测量三个睁开阶段的特点：4、摄影测量存在哪些问题第二章单幅影像解析基础1、像主点：摄像机主光轴〔摄影方向〕与像平面的交点，称为像片主点。

像主距：摄像机物镜后节点到像片主点的垂距称为摄像机主距，也叫像片主距〔f〕。

2、航空摄影：利用安装在航摄飞机上的航摄仪，在空中以预定的翱翔高度度沿着早先拟定好的航线翱翔，按必然的时间间隔进行曝光摄影，获取整个测区的航摄像片。

空中摄影采用竖直摄影方式，即摄影刹时摄像机物镜主光轴近似与地面垂直。

1lfmL H〔m—像片比率尺分母，f—摄像机主距，H—平均高程面的摄影高度H=m・f〕3、相对航高是指摄像机物镜有对于某一基准面的高度，称为摄影航高。

绝对航高是有对于平均海平面的航高，是指摄像机物镜在摄影刹时的真实海拔高。

经过相对航高H与摄影地区地面平均高度H地计算获取：H绝二日+H4、航空摄影与成图比率尺的关系5、航向重叠：同一条航线内相邻像片之间的影像重叠称，重叠度一般要求在60%以上;旁向重叠：两相邻航带像片之间的影像重叠，重叠度要求在30%左右。

6、中心投影：当投影汇聚于一点时，称为中心投影；正射投影：投隐射线与投影平面成正交。

中心投影：投隐射线汇聚于一点〔投隐射线的汇聚点称投影中心〕投影斜投影：投隐射线与投影平面成斜交I平行投影II正射投影：投隐射线与投影平面成正交7、透视变换中的重要的点线面：① 由投影中心作像片平面的垂线，交像面于o ，称为像主点；像主点在地面上的对应点以 O 表示，称为地主点。

② 由摄影中心作铅垂线交像片平面于点n ，称为像底点；此铅垂线交地面于点N ，称为地 底点。

③ 过铅垂线SnN 和摄影方向SoO 的铅垂面称为主垂面〔W 〕，主垂面即垂直于像平面P ， 又垂直于地平面E ，也垂直于两平面的交线透视轴TT 。

多视角几何5-相机模型-射影相机一般射影相机P通过x=PX将世界点X映射到图像点x。

基于这种映射，我们将对相机模型进行分解，进一步展示几何实体，如相机中心，如何起作用。

我们所考虑的一些性质仅应用于有限射影相机和它们的推广，而其他性质则适用于一般相机。

这种区别在上下文中很容易区分，有关性质参考下表：5.2.1 相机模型拆解一般射影相机可分解为若干部分，P=[M | p4]，其中M是3×3矩阵。

我们可以证明，如果M是非奇异矩阵，那么这是一个有限相机，否则不是。

相机中心.矩阵P有一维零空间，因为它的秩是3，并且有4列。

假设零空间是由4维向量C组成，即PC=0。

现在可以证明，C是相机中心，并以4维齐次向量组成。

考虑包含C 和三维空间中任意点A的直线。

该直线上的点可以通过连接表示，X(λ)=λA+(1-λ)C。

在映射x=P X作用下，该直线上的点投影是，x=Px=PX(λ)=λPA+(1-λ)PC=λPA因为PC=0。

直线上所有点均映射到同一个图像点PA，这表示，该直线一定是经过相机中心的射线，也推出C是相机中心的齐次表达式，因为对于A的所有选择，直线X(λ)都是通过相机中心的一条射线。

这个结果在预料之内，因为图像点(0,0,0)T=PC并未定义，相机中心是空间中唯一的图像没有定义的点。

在有限相机情况下，可直接求得相机中心，因为C=(T,1)T显然是P=KR[ I | -]的零向量。

这个结论是正确的，即使P的3×3子矩阵M 是奇异的。

在奇异情况下，尽管零向量的形式C=(d T,0)T，其中Md=0。

相机中心是无穷远点，这种相机模型会在5.3中讨论。

列向量.射影相机的列是三维向量，是具有几何意义代表着某个图像点。

采用记号p i 表示P的各列，i=1....4，那么p1，p2，p3分别表示X/Y/Z轴的消失点。

这是因为这些点是轴方向的图像。

例如，x轴的方向D=(1,0,0,0)T，它成像在p1=PD，参考图。