角边角定理

角角边定理经典数学定理角角边定理又称三角形三边定理，是由古希腊数学家艾西莫斯提出的。

它最早出现在他的著作《数学史》中，它的基本思想是：如果三条边的长度分别为a、b、c，则“a+b>c”。

角角边定理是一个关于三角形的重要定理，它是非常重要的一个基础定理，在很多数学问题中，它都使用到了。

它能够提供用户对三角形及其角边的重要信息，例如求解三角形三条边长度等。

早在古希腊时期，定理就已经被提出。

当时，数学家艾西莫斯就已经得出了三角形的三边规律，即“a+b>c”。

此外，他还发现，当三角形的某一边较长时，对应的两个角就会变小。

这就是角角边定理的基本思想。

古代数学家认为，三角形的三边的长度应当符合a+b>c的关系，否则就不能构成三角形。

在18世纪，英国数学家约翰杰斐逊将这一定理推广到了几何学中，他把它称为“角角边定理”。

杰斐逊把它应用到了多边形，证明了它对求解多边形的面积和周长也有着重要的意义。

角角边定理也可以用于求解其他几何问题。

比如，它可以用来计算三角形内角平分线的长度，也可以用来求解三角形的外接圆半径。

它还可以用来求解斜三角形的面积，也可以用来求解椭圆的周长等等。

角角边定理也在现代几何学中得到了广泛应用，它在很多几何问题的求解中都起着重要的作用。

比如，它可以用来计算正多边形的内角和外角，可以用来求解正多边形的面积和周长，甚至可以用来求解曲线的交点等等。

由于角角边定理在几何学中有着重要的作用，因此，它已经被定义为几何学的基本定理。

它不仅在数学领域有着重要的应用，而且在工程学中也有很多应用。

比如，在建筑工程中，它可以用来设计几何形状，用来求解室内墙体的面积和角度等等。

显然，角角边定理是一个非常重要的几何定理，它在很多几何问题中都发挥着重要的作用。

它的作用和意义不仅仅是几何学中的，它在工程学中也有重要的应用。

希望本文可以帮助读者更好地理解角角边定理，并将它应用到实践中。

三角形全等的边角边判定定理的由来三角形全等的边角边判定定理是几何学中一个重要的判定全等三角形的定理，它指出，如果两个三角形的一个角和两边分别与另一个三角形的一个角和两边相等，那么这两个三角形全等。

下面将详细介绍这个定理的由来。

边角边判定定理最早可以追溯到古希腊时期的几何学家欧几里得（Euclid）。

欧几里得在他的著作《几何原本》（Elements）中系统地阐述了欧几里得几何的基本原理和定理，边角边判定定理就是其中的一条。

在欧几里得的几何系统中，全等的概念是一个基本的概念。

两个几何图形全等意味着它们具有相同的形状和大小。

欧几里得通过不同的方法证明了一些三角形的全等判定定理，比如SAS（边角边）、SSS （边边边）和ASA（角边角）等定理，这些定理在后来的几何学研究中得到了广泛应用。

边角边判定定理的证明一般采用辅助线的方法。

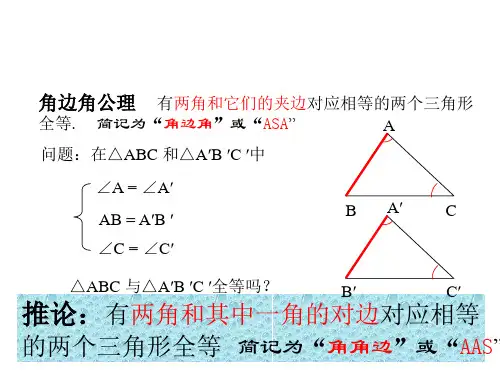
首先，我们假设有两个三角形ABC和DEF，假设∠ABC=∠DEF，AB=DE，BC=EF。

我们需要证明这两个三角形全等。

为了证明这个定理，我们可以引入一个辅助线，将两个三角形重叠在一起。

首先，我们可以在两个三角形的共同顶点B和E之间画一条线段BE，然后通过顶点B和E分别画出射线BA和ED。

由于∠ABC=∠DEF，所以射线BA和射线ED的方向是一样的。

然后，我们可以利用已知条件AB=DE和BC=EF，将BE分别延长到交点C和F。

根据欧几里得的几何原理和已知条件，我们可以得到下列结论：1. ∠ABC=∠DEF（已知）；2. AB=DE（已知）；3. BC=EF（已知）；4. ∠ABE=∠BDE（公共角）；5. ∠BCA=∠EFA（公共角）。

根据欧几里得几何的公理和等角的定义，我们可以得到以下等式：1. ∠ABC=∠DEF（已知）；2. AB=DE（已知）；3. BC=EF（已知）；4. ∠ABE=∠BDE（公共角）；5. ∠BCA=∠EFA（公共角）；6. AC=AF（共线）。

由于两个三角形的三个边和三个角分别相等，满足等价性的条件，所以我们可以得出结论，两个三角形ABC和DEF全等。

三角形的全部定理
三角形是几何学中最基本的形状之一，它具有丰富的性质和定理。

三角形的全部定理是一系列关于三角形边长、角度和面积的定理。

1. 三角形的内角和定理（角度定理）：任意三角形的三个内角之和等于180度。

这个定理有助于计算未知角度，或者判断给定角度是否构成三角形。

2. 三角形的外角和定理：任意三角形的一个外角等于其余两个内角
之和。

这个定理可以帮助我们计算外角的大小。

3. 三角形的边长关系定理（边长定理）：在任意三角形中，任意两边之和大于第三边。

这个定理可以用来判断给定的边长是否能够构成一个三角形。

4. 三角形的角边关系定理（角边定理）：在任意三角形中，两个角的夹边之比等于这两个角的正弦之比。

这个定理可以用来计算或比较三角形的边长和角度。

5. 三角形的正弦定理：在任意三角形中，三个角的正弦之比等于对
边的长度之比。

这个定理可以用来计算未知边长或角度。

6. 三角形的余弦定理：在任意三角形中，边的平方等于另外两边平方之和减去这两边与这个边所夹角的余弦乘积的两倍。

这个定理可以用来计算未知边长或角度。

除了上述定理外，还有许多其他与三角形相关的定理，如角平分线定理、中位线定理、高线定理等等。

这些定理在解决三角形相关问题、计算三角形的面积、判断三角形的形状等方面都有重要的应用。

掌握这些定理可以帮助我们更好地理解和分析三角形的性质。

三角形边边角公式
三角定律，简单的说就是五条数学定律。

正弦定理、余弦定理、直角三角形中的射影定理、大角对大边定理、内角平分线定理。

该定律的作用，是通过对行情前期图形的角度形态来判断未来走势的方向及潜力。

把人们常说的“盘感”用数学几何图形做出逻辑的诠释。

该定律有助于对大周期，小周期之间的结构关系进行全局性的理解。

对临界点的发现有极其精确的锁定。

三角定律是对趋势结构阐述的最为精辟的理论之一。

等边三角形（ 又称正三边形），为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。

等边三角形也是最稳定的结构。

等边三角形是特殊的等腰三角形，所以等边三角形拥有等腰三角形的一切性质。

三角形的边角关系公式为：
1、正弦定理：a/sinA=b/sinB=c/sinC。

2、余弦定理：a²=b²+c²-2bccosA，b²=a²+c²-2accosA，c²=a²+b²-2abcosA。

三角形角角边定理一、角角边定理（AAS）的内容1. 定义- 在两个三角形中，如果有两个角和其中一个角的对边分别相等，那么这两个三角形全等。

- 例如，在△ABC和△DEF中，如果∠A = ∠D，∠B=∠E，BC = EF（∠A和∠D，∠B和∠E是两角，BC是∠A的对边，EF是∠D的对边），那么△ABC≌△DEF。

二、角角边定理的证明1. 思路- 已知两个三角形有两个角相等，根据三角形内角和为180°，可以推出第三个角也相等。

然后利用已经有的角相等和一条边相等的条件，通过转化为角边角（ASA）定理来证明三角形全等。

2. 证明过程（以△ABC和△DEF为例，∠A = ∠D，∠B = ∠E，BC=EF）- 因为∠A = ∠D，∠B = ∠E，又因为三角形内角和为180°，所以在△ABC中，∠C=180° - ∠A - ∠B；在△DEF中，∠F = 180°-∠D - ∠E。

- 由于∠A = ∠D，∠B = ∠E，所以∠C = ∠F。

- 在△ABC和△DEF中，已经有∠B = ∠E，BC = EF，∠C = ∠F，根据角边角（ASA）定理，可以得出△ABC≌△DEF。

三、角角边定理的应用1. 证明三角形全等- 例1：已知在△ABC和△DEF中，∠A = 30°，∠B = 50°，BC = 4cm，∠D = 30°，∠E = 50°，EF = 4cm。

- 因为∠A = ∠D = 30°，∠B = ∠E = 50°，BC = EF = 4cm，根据角角边（AAS）定理，所以△ABC≌△DEF。

2. 求解三角形中的未知元素- 例2：在△ABC中，∠A = 40°，∠B = 60°，AC = 5cm。

在△DEF中，∠D = 40°，∠E = 60°，DF = 5cm。

- 由角角边（AAS）定理可知△ABC≌△DEF。

角与边的关系公式角与边的关系是几何学中的重要概念之一，它描述了角度和边长之间的数学关系。

在几何学中，角度通常被表示为两条边之间的夹角，而边长则是指连接角的两个点之间的距离。

在平面几何中，角度可以分为直角、锐角和钝角三种类型。

其中，直角是指两条边相互垂直，形成一个90度的角；锐角是指两条边之间的夹角小于90度；钝角则是指两条边之间的夹角大于90度。

角与边的关系可以通过一些公式来描述。

以下是几个常见的角与边的关系公式：1. 正弦定理：正弦定理描述了一个三角形中的角与边的关系。

对于一个三角形ABC，边长分别为a、b、c，而角A、B、C的对边分别为a、b、c，则正弦定理可以表示为：sin(A)/a = sin(B)/b = sin(C)/c2. 余弦定理：余弦定理也描述了一个三角形中的角与边的关系。

对于一个三角形ABC，边长分别为a、b、c，而角A、B、C的对边分别为a、b、c，则余弦定理可以表示为：c^2 = a^2 + b^2 - 2ab*cos(C)3. 正切定理：正切定理描述了一个直角三角形中的角与边的关系。

对于一个直角三角形ABC，边长分别为a、b，而角A、B的对边分别为a、b，则正切定理可以表示为：tan(A) = a/b4. 角平分线定理：角平分线定理描述了一个角的平分线与角的边之间的关系。

对于一个角ABC，其平分线交角的边AB和AC分别于D和E，则有：AB/BD = AC/CE以上公式是角与边的关系中常用的几个公式，它们在解决几何问题和计算角度和边长时非常有用。

通过这些公式，我们可以在已知一些角或边的情况下，计算出其他未知角或边的值。

除了这些公式外，还有一些特殊情况下的角与边的关系。

例如，在等边三角形中，三个角均为60度；在等腰直角三角形中，两个锐角均为45度。

这些特殊情况下的角与边的关系也有助于我们更好地理解几何学中的角与边的概念。

总结起来，角与边的关系是几何学中的重要概念之一。

通过一些公式和特殊情况下的关系，我们可以计算和解决与角度和边长相关的几何问题。

边边角定理
边边角定理指的是两三角形中，如果两组对应的边相等，并且其中一组等边的对角相等，那么这两个三角形全等。

具体来说，如果两个三角形有两条边相等，并且这两条边所夹的角也相等，那么这两个三角形就是全等的。

这个定理可以用来证明两个三角形是否全等。

需要注意的是，边边角定理并不适用于所有情况。

如果两个三角形只有一组对应边相等，且这两条边所夹的角为钝角或直角，或者不是对应角，那么这两个三角形不一定全等。

因此，在使用边边角定理时，需要仔细检查条件是否满足，以避免出现错误。

另外，还需要注意的是，在边边角定理中，“对应角相等”这个条件是很重要的。

如果没有这个条件，那么两个三角形就不一定全等。

因此，在使用边边角定理时，需要确保这个条件也被满足。

总之，边边角定理是一个有用的定理，可以用来证明两个三角形是否全等。

但是，在使用时需要注意条件是否满足，以避免出现错误。