下载文档原格式
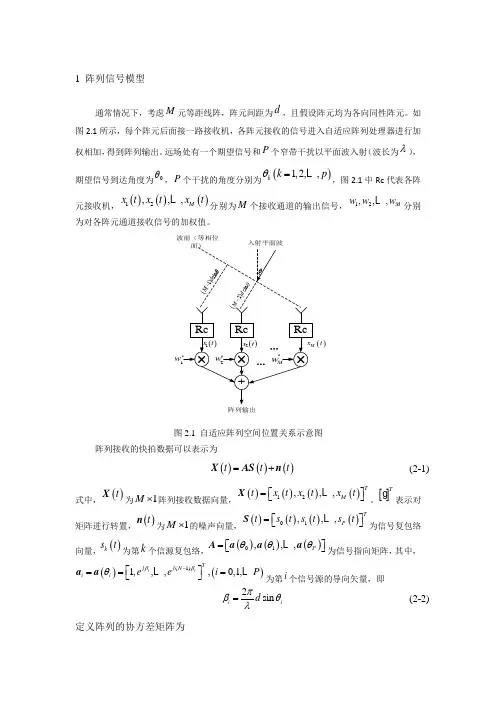
1 阵列信号模型通常情况下，考虑M 元等距线阵，阵元间距为d ，且假设阵元均为各向同性阵元。
如图2.1所示，每个阵元后面接一路接收机，各阵元接收的信号进入自适应阵列处理器进行加权相加，得到阵列输出。
远场处有一个期望信号和P 个窄带干扰以平面波入射（波长为λ），期望信号到达角度为0θ，P 个干扰的角度分别为()1,2,,k k p θ= ，图2.1中Rc 代表各阵元接收机，()()()12,,,M x t x t x t 分别为M 个接收通道的输出信号，12,,,M w w w 分别为对各阵元通道接收信号的加权值。
()t w 阵列输出波前（等相位图2.1 自适应阵列空间位置关系示意图阵列接收的快拍数据可以表示为()()()t t t =+X AS n(2-1)式中，()t X 为1M ⨯阵列接收数据向量，()()()()12,,,TM t x t x t x t =⎡⎤⎣⎦X 。
[]T表示对矩阵进行转置，()t n 为1M ⨯的噪声向量，()()()()01,,,TP t s t s t s t =⎡⎤⎣⎦S 为信号复包络向量，()k s t 为第k 个信源复包络，()()()01,,,P θθθ=⎡⎤⎣⎦A a a a 为信号指向矩阵，其中，()()(1)1,,,,0,1,i iTj j N i i e e i P ββθ-⎡⎤===⎣⎦a a 为第i 个信号源的导向矢量，即2sin i i d πβθλ=(2-2)定义阵列的协方差矩阵为()()2H H x s n E t t σ⎡⎤==+⎣⎦R X X AR A I (2-3)式中，()()H s E t t ⎡⎤=⎣⎦R S S 为信号的协方差矩阵，I 为M 维单位矩阵，2n σ为阵元的噪声功率，本文中约定，[]T表示转置，[]*表示共轭，[]H表示共轭转置。
式(2-3)常由接收数据采样协方差矩阵ˆx R 代替，即()()11ˆNH xiii t t N==∑R x x(2-4)如图2.1所示的自适应阵列模型，阵列的M 个通道接收信号经加权处理后，最后的输出信号为()()()1MH i i i y t w x t t *===∑w x(2-5)阵列的方向图()p θ定义为()()H p θθ=w a(2-6)调整自适应阵列的权矢量w ，可以改变阵列的方向图，即改变各个方向上入射信号增益。
阵列信号处理（Array Signal Processing）1. 简介阵列信号处理是一种利用多个传感器或微phones接收到的信号进行处理的技术。
这些传感器通常以阵列的形式排列在一起，可以在空间上对信号进行采样。
阵列信号处理技术可以用于各种应用，包括无线通信、雷达、声音定位和语音增强等领域。
在阵列信号处理中，经常会使用到点扩散函数（Point Spread Function，PSF）和反卷积（Deconvolution）等概念。
本文将详细介绍这些特定函数的定义、用途和工作方式。
2. 点扩散函数（Point Spread Function，PSF）2.1 定义点扩散函数（PSF）是指在观察到一个点源时，系统输出的响应。
点源可以是一个理想的点光源、点声源或点热源等。
PSF描述了系统对于一个点源的感知能力，可以用于评估系统的分辨率和信号传输特性。
2.2 用途PSF在阵列信号处理中具有广泛的应用，主要用于以下几个方面：2.2.1 分辨率评估PSF可以用于评估系统的分辨率，即系统能够分辨并显示的最小特征尺寸。
通过分析PSF的形状和尺寸，可以确定系统的分辨率限制，进而优化系统设计和参数设置。
2.2.2 反卷积PSF还可以用于图像或信号的反卷积处理。
在实际应用中，由于传感器和系统的限制，观测到的信号往往受到模糊和失真的影响。
通过将观测到的信号与PSF进行卷积运算的逆过程，可以恢复出原始信号的更清晰的图像或声音。
2.2.3 信号重构PSF在阵列信号处理中也可以用于信号重构。
通过对多个传感器接收到的信号进行处理和分析，可以利用PSF将信号的不同成分分离出来，从而实现信号的重构和定位。
2.3 工作方式PSF的工作方式可以通过以下几个步骤来理解：2.3.1 系统建模首先，需要对阵列系统进行建模。
这包括确定阵列的几何结构、传感器的位置和响应特性等。
通过建模，可以得到系统的传递函数，即系统对于输入信号的响应。
2.3.2 点源输入接下来，将一个点源输入到系统中，观察系统的输出。
基于MATLAB阵列信号处理研究1基于MATLAB阵列信号处理研究1MATLAB是一种广泛应用于科学和工程领域的编程语言和开发环境。
它在信号处理领域有着广泛的应用，可以用于信号的生成、滤波、变换、分析和可视化等方面。
本文将基于MATLAB介绍阵列信号处理的研究内容，包括阵列信号模型、阵列信号参数估计、波束形成和空间谱估计等。
首先，阵列信号模型是研究阵列信号处理的基础。
阵列信号模型描述了信号在阵列中的传播和接收过程。
常见的阵列信号模型有基于阵列几何结构的波达模型和基于信号方向的自相关函数模型。
波达模型假设信号到达阵列的时间差和入射角与信号源之间的关系，自相关函数模型则描述了信号在阵列中的空间相关性。
其次，阵列信号参数估计是研究阵列信号处理的关键环节。
信号参数估计是指在阵列接收到信号之后，通过分析接收到的信号来估计信号的到达角度、入射波的相位和幅度等参数。
常用的信号参数估计方法有基于阵列输出的MUSIC算法、基于最小二乘法的MVDR算法和基于梯度的阵列信号处理算法等。
这些方法可以有效地提取出信号的参数信息并进行分析。
波束形成是阵列信号处理的一个重要任务。
波束形成是指通过对阵列接收到的信号进行加权和相干性处理，实现对特定方向信号的增强，从而抑制其他方向的干扰信号。
常用的波束形成方法有波束形成权向量设计、线性约束波束形成和非线性约束波束形成等。
这些方法可以实现对特定方向的信号进行增强，并提高抗干扰能力和信噪比。
最后，空间谱估计是一种用于估计信号频谱特性的方法。
空间谱估计可以通过阵列接收到的信号的二阶统计特性来计算信号的功率谱密度。
常用的空间谱估计方法有基于传统阵列信号处理方法的峰值检测算法、基于最大似然法的多传感器信号处理算法和基于SVD分解的阵列信号处理算法等。
这些方法可以提供信号的频谱信息，为信号处理和分析提供重要的依据。
总之，基于MATLAB的阵列信号处理研究涉及到阵列信号模型、信号参数估计、波束形成和空间谱估计等多个方面。
信号子空间：设N 元阵接收p 个信源，则其信号模型为：()()()()1piiii x t s t a N t θ==+∑在无噪声条件下，()()()()()12,,,P x t span a a a θθθ∈称()()()()12,,,P span a a a θθθ为信号子空间，是N 维线性空间中的P 维子空间，记为P N S 。
P N S 的正交补空间称为噪声子空间，记为N P N N -。
正交投影设子空间m S R ∈，如果线性变换P 满足，()1),,,2),,,0m mx R Px S x S Px x x R y S x Px y ∀∈∈∀∈=∀∈∀∈-=且则称线性变换P 为正交投影。
导向矢量、阵列流形设N 元阵接收p 个信源，则其信号模型为：()()()()1piiii x t s t a N t θ==+∑，其中矢量()i ia θ称为导向矢量，当改变空间角θ，使其在空间扫描，所形成的矩阵称为阵列流形，用符号A 表示，即(){|(0,2)}a A θθπ=∈波束形成波束形成（空域滤波）技术与时间滤波相类似，是对采样数据作加权求和,以增强特定方向信号的功率，即()()()()HHy t W X t s t W a θ==，通过加权系数W 实现对θ的选择。
最大似然已知一组服从某概率模型()f X θ的样本集12,,,N X X X ，其中θ为参数集合，使条件概率()12,,,N f X X X θ最大的参数θ估计称为最大似然估计。
不同几何形态的阵列的阵列流形矢量计算问题假设有P 个信源，N 元阵列，则先建立阵列的几何模型求第i 个信源的导向矢量()i i a θ 选择阵元中的一个作为第一阵元，其导向矢量()1[1]i a θ=然后根据阵列的几何模型求得其他各阵元与第一阵元之间的波程差n ∆，则确定其导向矢量()2jn i a eπλθ∆=最后形成N 元阵的阵列流形矢量()11221N j j N Pe A e πλπλθ-∆∆⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 例如各向同性的NxM 元矩形阵，阵元间隔为半个波长，当信源与阵列共面时：首先建立阵列几何模型：对于第m 行、第n 列的阵元，其与第1行、第1列阵元之间的波程差为(1)sin()(1)cos()mn i i n d m d θθ∆=---故：()1122(sin()cos())22((1)sin()(1)cos())11N j j d j j d N M NM P NM Pe e A e e ππθθλλππθθλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦而当信源与阵列不共面时： 首先将信源投影到阵列平面然后建立阵列模型对于第m 行、第n 列的阵元，其与第1行、第1列阵元之间的波程差为[(1)sin()(1)cos()]sin()mn i i i n d m d θθϕ∆=-+-故：()1122(sin()cos())cos()22((1)sin()(1)cos())cos()11N j j d j j d N M NM P NM Pe e A e e ππθθϕλλππθθϕλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦线性约束最小方差准则（LCMV ）的自适应波束形成算法： 对于信号模型：()()()0X t s t a J N θ=++， 波束形成输出：()()()()0()H H H yt W X t s t W a W J N θ==++LCMV 准则实际上是使()0HW a θ为一个固定值的条件下，求取使得()HWJ N +方差最小的W 作为最有权值，即：()0min .H X W HW R Ws t W a Fθ⎧⎪⎨⎪=⎩，其中F 为常数利用拉格朗日乘子法可解得：()10X opt W R a μθ-=当取1F =时，则()()11H X a R a μθθ-=，μ的取值不影响SNR 和方向图。
阵列接收信号处理流程一、信号接收阵列接收信号处理的第一步是信号接收。
在阵列中，有多个接收器同时接收信号。
这些接收器可以是天线、传感器或其他接收设备。
每个接收器都可以独立地接收到信号，并将信号传输到后续的信号处理单元。
二、信号预处理接收到的信号可能会受到噪声、干扰或其他不完美因素的影响，因此需要进行信号预处理。
信号预处理的目的是提高信号的质量和准确性。
常见的信号预处理方法包括滤波、增益控制、噪声消除和时序校正等。
滤波是信号预处理的一种常用方法。
通过滤波可以去除信号中的噪声和干扰，提高信号的清晰度和可辨识度。
常见的滤波方法有低通滤波、高通滤波和带通滤波等。
增益控制是调整信号强度的方法。
通过增益控制可以使信号的强度达到最佳状态，避免信号过强或过弱的问题。
噪声消除是去除信号中噪声成分的方法。
噪声是信号中的不完美因素，可能会干扰信号的质量和准确性。
通过噪声消除可以提高信号的清晰度和准确性。
时序校正是调整信号的时序关系的方法。
在多个接收器同时接收信号时，由于信号传输路径的不同，信号到达各个接收器的时间可能存在微小的差异。
通过时序校正可以使信号的时序关系达到一致，提高信号的同步性和准确性。
三、信号合并经过信号预处理后，接收到的信号可以进行合并。
信号合并是将多个接收器接收到的信号进行综合和整合的过程。
通过信号合并可以提高信号的强度和准确性，增加信号的可靠性和鲁棒性。
常见的信号合并方法有加权平均法、最大比例合并法和最大比例合并法等。
加权平均法是将每个接收器接收到的信号按照一定的权重进行加权平均，得到综合的信号。
最大比例合并法是选择接收到信号强度最大的接收器的信号作为综合的信号。
最大比例合并法是根据接收到信号的强度比例进行综合，提高信号的强度和准确性。
四、信号解调和解码信号合并后，接下来需要进行信号的解调和解码。
信号解调是将调制信号转化为原始信号的过程。
常见的调制方式有频率调制、相位调制和振幅调制等。
通过信号解调可以恢复出原始信号的特征和信息。
阵列信号处理是信号处理的一个年青的分支，属于现代信号处理的重要研究内容之一，其应用范围很广，可用于雷达、声呐、通信、地震勘察、射电天文和医用成像等众多领域。
阵列信号处理是将一组传感器在空间的不同位置按一定规则布置形成的传感器阵列（尽管采用的传感器的类型可以不同，如天线、水听器、听地器、超声探头、X射线检测器，但是传感器的功能是相同的，它是连接信号处理器和感兴趣的空间纽带），用传感器阵列发射能量和（或）接收空间信号，获得信号源的观测数据并加以处理。
阵列信号处理的目的是从这些观测数据中提取信号的有用特征，获取信号源的属性等信息。
目前，阵列信号处理在雷达及移动通信等领域有着广泛而重要的应用。
在相控阵雷达体制中，自适应波束形成技术在抑制杂波干扰方面起着关键的作用。
在移动通信中，基于阵列信号处理的波达方向估计技术，使移动通信进入一个崭新的阶段。
本论文首先介绍阵列信号处理的基础知识。
在此基础上，着重讨论阵列波束形成技术，非理想线性阵列的雷达信号波达方向和多普勒频率估计，均匀圆形阵列的信号波达方向估计和复杂信号的波达方向及参数估计等四方面内容。
这些内容都是阵列信号处理领域的研究热点。
它们无论对阵列信号处理的理论发展还是实际应用，都有重要的意义。
目前，人们普遍关注在阵列响应矢量未知情况下，自适应波束形成问题，即盲自适应波束形成技术。
本文第一方面介绍了最基本的阵列波束形成方法，即最小均方误差波束形成器，线性约束最小方差波束形成器和基于特征空间的波束形成器（ESB）。
在此基础上，提出一个基于特征空间的盲自适应波束形成算法。
此算法首先根据高分辨波达方向估计方法，估计信号源的波达方向，然后以此方向形成约束导向矢量，进而计算出ESB波束形成算法的最优权矢量，最后，对期望目标形成笔状波束。
此算法能够有效地抑制信号的对消现象，并且能够应用于在波束中有多个期望信号的场合。
当阵列存在各种误差时，一般高分辨波达方向估计方法（如MUSIC）的估计性能严重下降。
