5.6三角函数的图像和性质

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinαcos （2kπ＋α）= cosαtan （2kπ＋α）= tanαcot （2kπ＋α）= cotα设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= -sinαcos（π＋α）= -cosαtan（π＋α）= tanαcot（π＋α）= cotα公式三任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明（全部）公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注：韦达定理判别式b2-4a=0 注：方程有相等的两实根b2-4ac>0 注：方程有一个实根b2-4ac<0 注：方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注：角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。

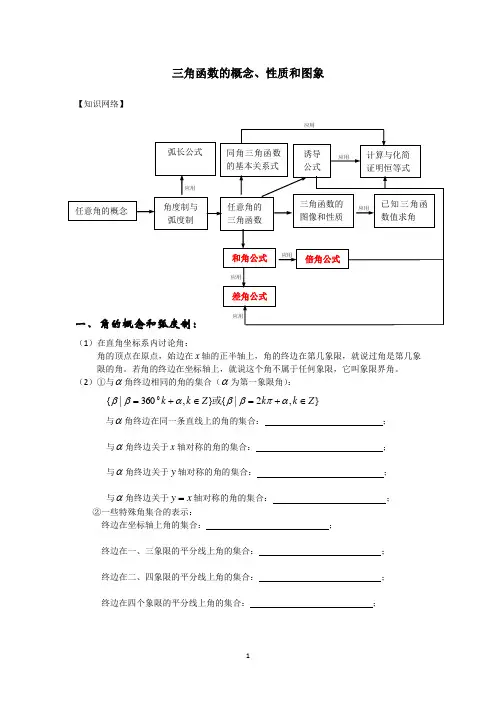
三角函数的概念、性质和图象【知识网络】一、角的概念和弧度制：（1）在直角坐标系内讨论角：角的顶点在原点，始边在x 轴的正半轴上，角的终边在第几象限，就说过角是第几象限的角。

若角的终边在坐标轴上，就说这个角不属于任何象限，它叫象限界角。

（2）①与α角终边相同的角的集合（α为第一象限角）： },2|{},360|{0Z k k Z k k ∈+=∈+=απββαββ或与α角终边在同一条直线上的角的集合： ；与α角终边关于x 轴对称的角的集合： ；与α角终边关于y 轴对称的角的集合： ；与α角终边关于x y =轴对称的角的集合： ；②一些特殊角集合的表示：终边在坐标轴上角的集合： ；终边在一、三象限的平分线上角的集合： ；终边在二、四象限的平分线上角的集合： ；终边在四个象限的平分线上角的集合： ；任意角的概念弧长公式角度制与 弧度制 同角三角函数的基本关系式诱导 公式计算与化简 证明恒等式任意角的 三角函数三角函数的 图像和性质已知三角函数值求角和角公式倍角公式差角公式应用应用应用应用应用应用应用（3）区间角的表示：①象限角：第一象限角： ；第三象限角： ；第一、三象限角： ；②写出图中所表示的区间角：（4）弧度制：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零；任一已知角α的弧度数的绝对值rl=||α，其中l 为以角α作为圆心角时所对圆弧的长，r 为圆的半径。

（5）弧长公式： ；扇形面积公式： ；二、任意角的三角函数：（1）任意角的三角函数定义：以角α的顶点为坐标原点，始边为x 轴正半轴建立直角坐标系，在角α的终边上任取一个异于原点的点),(y x P ，点P 到原点的距离记为r ，则=αsin ；=αcos ；=αtan ；=αc s c ；=αsec ；=αcot ； 如：角α的终边上一点)3,(a a -，则=+ααsin 2cos 。

（2）在图中画出角α的正弦线、余弦线、正切线；比较)2,0(π∈x ，x sin ，x tan ，x 的大小关系： 。

【课题】5.6三角函数的图像和性质
【教学目标】
知识目标：
(1) 理解正弦函数的图像和性质；
(2) 理解用“五点法”画正弦函数的简图的方法；
(3) 了解余弦函数的图像和性质．
能力目标：
(1) 认识周期现象，以正弦函数、余弦函数为载体，理解周期函数；
(2) 会用“五点法”作出正弦函数、余弦函数的简图；
(3) 通过对照学习研究，使学生体验类比的方法，从而培养数学思维能力．
【教学重点】
（1）正弦函数的图像及性质；
（2）用“五点法”作出函数y=sin x在[]
0,2π上的简图．
【教学难点】
周期性的理解．
【教学设计】
（1）结合生活实例，认识周期现象，介绍周期函数；
（2）利用诱导公式，认识正弦函数的周期；
（3）利用“描点法”及“周期性”作出正弦函数图像；
（4）观察图像认识有界函数，认识正弦函数的性质；
（5）观察类比得到余弦函数的性质．
【教学备品】
课件，实物投影仪，三角板，常规教具．
【课时安排】
1
2课时．(90分钟)
【教学过程】
2
及
3
，
一般地，设函数y=
，对任意的
．如果这样的M
无界函数．
4。

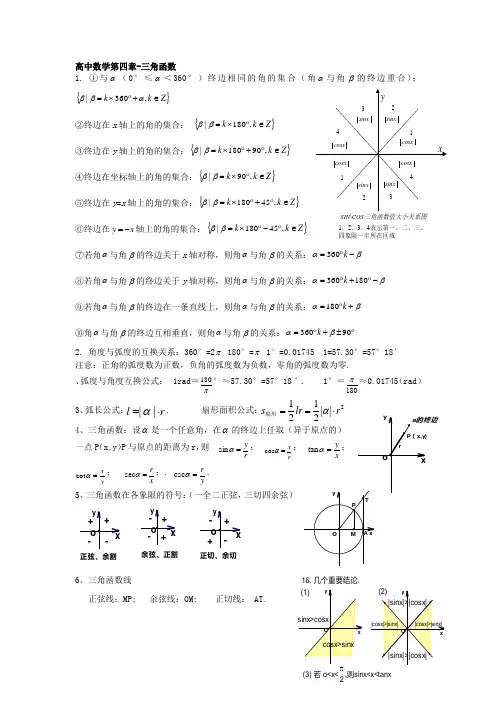
三角函数图像与性质三角函数的图像与性质一、正弦函数和余弦函数的图像：正弦函数y=sinx和余弦函数y=cosx的图像可以用五点法作图。

先取横坐标分别为-2π,-π,0,π,2π的五个点，再用光滑的曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图像。

二、正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的性质：1.定义域：都是R。

2.值域：1）都是[-1,1]。

2）正弦函数y=sinx，当x=2kπ+3π/2(k∈Z)时，y取最小值-1；当x=2kπ+π/2(k∈Z)时，y取最大值1.余弦函数y=cosx，当x=2kπ(k∈Z)时，y取最大值1；当x=2kπ+π(k∈Z)时，y取最小值-1.3.周期性：1）正弦函数y=sinx、余弦函数y=cosx的最小正周期都是2π。

2）函数f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)的最小正周期都是T=2π/|ω|。

4.奇偶性与对称性：1）正弦函数y=sinx是奇函数，对称中心是(2kπ,0)(k∈Z)，对称轴是直线x=kπ+π/2(k∈Z)。

2）余弦函数y=cosx是偶函数，对称中心是(kπ,0)(k∈Z)，对称轴是直线x=kπ(k∈Z)。

例：若函数y=a-bsin(3x+π/6)的最大值为1，最小值为-2，则a=1/2，b=1或b=-1.课堂练：1.函数y=sinx-sin2x的值域是[-1,1]。

2.已知f(x)的定义域为[0,1]，求f(cosx)的定义域为[-1,1]。

3.下列函数中，最小正周期为π的是B.y=sin2x。

4.若f(x)=sin(πx/3)，则f(1)+f(2)+f(3)+。

+f(2003)=0.答：1001/2）正弦型函数的对称轴为过最高点或最低点且垂直于x轴的直线，对称中心为图象与x轴的交点。

例如，函数y=sin(5π/2x)的奇偶性是偶函数。

已知函数f(x)=ax+bsin(3x)+1(a,b为常数），且f(5)=7，则f(-5)=-5.单调性方面，y=sinx在[2kπ-,2kπ+]（k∈Z）上单调递增，在[2kπ+,2kπ+]（k∈Z）上单调递减；y=cosx在[2kπ,2kπ+π]（k∈Z）上单调递减，在[2kπ+π,2kπ+2π]（k∈Z）上单调递增。

三角函数的图象与性质(解析版)三角函数的图象与性质(解析版)三角函数是数学中重要的函数之一，它们在解析几何、物理、工程等领域中具有广泛的应用。

本文将对三角函数的图象与性质进行解析，便于读者更好地理解与掌握三角函数的特点。

一、正弦函数的图象与性质正弦函数是最基本的三角函数之一，它的图象是一条连续的波浪线。

我们可以通过数学方法推导出正弦函数的周期性、奇偶性和对称性等性质。

1. 图象特点：正弦函数的图象是一条在坐标平面上连续波动的曲线。

它的振幅表示峰值与谷值之间的差距，周期则代表两个峰值或谷值之间的距离。

2. 周期性：正弦函数的一个周期内，曲线的形状相同，并且可以无限延伸。

周期为2π，即当x增加2π时，曲线的形状重复出现。

3. 奇偶性：正弦函数是奇函数，即f(x) = -f(-x)。

这意味着当自变量x取负值时，函数值会发生变号。

4. 对称性：正弦函数关于原点对称，即f(x) = -f(x + π)。

这意味着以原点为对称中心，曲线的左右两侧完全相同。

二、余弦函数的图象与性质余弦函数也是常见的三角函数之一，它的图象是一条连续的波浪线。

与正弦函数相似，余弦函数也有周期性、奇偶性和对称性等特点。

1. 图象特点：余弦函数的图象是一条波动的曲线，与正弦函数相比，它的最高点与最低点位置不同。

余弦函数的振幅表示波峰与波谷之间的差距，周期代表两个波峰或波谷之间的距离。

2. 周期性：余弦函数的周期也是2π，当自变量x增加2π时，曲线的形状重复出现。

3. 奇偶性：余弦函数是偶函数，即f(x) = f(-x)。

这意味着当自变量x取负值时，函数值保持不变。

4. 对称性：余弦函数关于y轴对称，即f(x) = f(π - x)。

这意味着以y轴为对称中心，曲线的左右两侧完全相同。

三、正切函数的图象与性质正切函数是三角函数中的另一个重要函数，它的图象是一条连续的波动曲线。

我们也可以通过数学方法推导出正切函数的周期性、奇偶性和对称性等性质。