当前位置：文档之家 › 第5章图与网络分析

第5章图与网络分析

  • 格式：ppt
  • 大小：5.72 MB
  • 文档页数：78

下载文档原格式

  / 78

合集下载

《运筹学》第8章_图与网络分析

《运筹学》第8章_图与网络分析
V = {v1 ,v 2 , v 3 , v 4 , v 5 , v 6 }
v1 e1 e2 e5 e8 v5 e6 e7 v3 v2 e3 e v4 4
e 5 = { v1 , v 3 }
e9 = {v 6 , v 6 }
E = {e1 ，2 , e3 , e4 , e5 , e6 , e7 , e8 , e9 , e10 } e e1 = {v1 , v 2 } e 2 = { v1 , v 2 } e10 e 3 = {v 2 , v 3 } e = {v , v }
引
C
言
B A
D
图的基本概念与基本定理
在实际的生产和生活中，人们为了 反映事物之间的关系，常常在纸上用点 点 和线来画出各式各样的示意图。 和线 是我国北京、上海、重庆等十四个城 市之间的铁路交通图，这里用点表示城 市，用点与点之间的线表示城市之间的 铁路线。诸如此类还有城市中的市政管 道图，民用航空线图等等。
例
v6
v1 3 6
4 7 3
v2 2 v3 5
3
4 2
权矩阵
v1 0 v 2 4 v 3 0 A= v4 6 v5 4 v6 3 v1
v5
v4
邻接矩阵
v1 0 v 2 1 v 3 0 B= v 4 1 v 5 1 v 6 1 v1 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 0 v 2 v 3 v4 v5 v6
4 3 4
e6 = {v 3 , v 5 }
e8 = {v 5 , v 6 } e10 = {v1 , v6 }
v6
e 7 = {v 3 , v 5 }

运筹学(第6章 图与网络分析)

运筹学(第6章 图与网络分析)
a1 (v1) 赵
(v2)钱
a2 a3 a4 a14 a15
a8 a9
a7 (v4) 李
(v3)孙
a5 (v5) 周 a6 a10 (v6)吴
图6-3
a12 a11 a13
(v7)陈

定义: 图中的点用v表示，边用e表示。对每条边可用它
所连接的点表示，记作：e1=[v1,v1]; e2=[v1,v2];
树是图论中结构最简单但又十分重要的图。在自然和社会领 域应用极为广泛。 例6.2 乒乓求单打比赛抽签后，可用图来表示相遇情况，如 下图所示。
运动员 A
B C
D
E
F G
H

例6.3 某企业的组织机构图也可用树图表示。
厂长
人事科
财务科
总工 程师
生产副 厂长
经营副 厂长
开发科
技术科
生产科
设备科
供应科
动力科
e2
(v1) 赵
e1
e3
e4 孙(v3) 李(v4)
周(v5)
图6-2
e5 吴(v6) 陈(v7)
(v2)钱
如果我们把上面例子中的“相互认识”关系改为“认识” 的关系，那么只用两点之间的联线就很难刻画他们之间的关 系了，这是我们引入一个带箭头的联线，称为弧。图6-3就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。
端点,关联边,相邻 若有边e可表示为e=[vi,vj]，称vi和
e2 v2 e6 e1 e4 v1 e3 v3 e8
vj是边e的端点，反之称边e为点vi
或vj的关联边。若点vi、vj与同一条 边关联，称点vi和vj相邻；若边ei和
e5
e7

计算机网络技术第5章网络层ppt课件

计算机网络技术第5章网络层ppt课件

5.2.1 在节点交换机中查找转发表
1. 广域网中的主机地址结构
+ 分组往往要经过许多节点交换机的存储转发才到达目的地。 + 每一个节点交换机中都有一个转发表，里面存放了到达每一个
主机的路由。那么广域网中的主机越多，查找转发表就越费时 间。 + 在广域网中一般采用层次地址结构:前一部分表示该主机所连接 的分组交换机的编号，后一部分表示所连接的分组交换机的端 口号（或主机号）。
3. 数据报和虚电路优缺点分析
1）传输短报文时数据报服务有优势 + 若报文长度较短，在128个字节之内，可采用128个
字节为分组长度，则往往一次传送一个分组就可以 了。这样，用数据报既迅速又经济。若用虚电路， 为了传送一个分组而建立虚电路和释放虚电路就很 浪费网络资源。 2）虚电路服务减少数据流量的额外开销 + 在交换节点进行数据存储转发时，若使用数据报， 每个分组必须携带完整的地址信息。而使用虚电路 时，每个分组不需要携带完整的目的地址，而仅需 要有个很简单的虚电路号码的标志，这就使分组的 控制信息部分比特数减少，因而减少了额外开销。
完成虚电路服务过程的步骤：
(1) 虚电路的建立 所谓建立一条虚电路，实际上就是填写源节点与目的节
点之间沿途各节点的入口出口表。 (2) 数据传送 虚电路建立后，所有待发的数据分组均由此虚电路传送。
这样，在传输一个分组时，分组头部不需要填入目的节 点的完整地址，只要带上虚电路号就可以了。 (3) 虚电路的释放 当数据传输结束后，源主机发一呼叫清除分组给目的主 机，目的主机送回一清除确认分组给源主机。至此，该 虚电路就释放了，即从入口出口表中删去相应信息。
– 当网络发生拥挤时，数据报服务可以迅速为单 个分组选择流量较少的路径。

图与网络分析

图与网络分析

end;
例 1 中 1 到 7 点的最短路是 1-2-5-7
查伴随矩阵 E 的第一行
1234567
10020255 19
hw
小结
• 最短路有广泛的应用 (P176案例) • 最短路的多种形式：无向图，有向图无循环圈，有向
图，混合图，无负边权，有负边权，有负回路，k-最 短路等 • 当存在负权值边时，Floyd算法比Dijkstra算法效率高， 且程序极简单。但Dijkstra算法灵活 • 若图是前向的，则Dijkstra算法也可以求两点间最长路 • 一般情况下，两点间最长路是 NP-complete，但最短 路是 P算法 • 两点间k-最短路：分为边不相交的和边相交的 求边不相交的k-最短路非常容易：先求最短路，将该 最短路中的边从网路删去，再用Dijkstra算法可求次最 短路，以此类推
hw
6.1.4 链，圈，路径，回路，连通图
• 走过图中所有边且每条边仅走一次的闭行走称为欧拉 回路
定理 2：偶图一定存在欧拉回路(一笔画定理) 6.1.4 连通图，子图，成分
• 设有两个图 G1(V1, E1), G2(V2, E2), 若V2 V1, E2 E1， 则 G2 是 G1 的子图
• 无向图中，若任意两点间至少存在一条路径，则称为 连通图(connected graph)，否则为非连通图( disconnected graph)；非连通图中的每个连通子图称为成分 (component)
线表示实体间的关联
A
A D
C
C
D
B
B
2
hw
6.1 图与网络的基本概念
6.1.1图与网络 • 节点 (Vertex)
– 物理实体、事物、概念 – 一般用 vi 表示

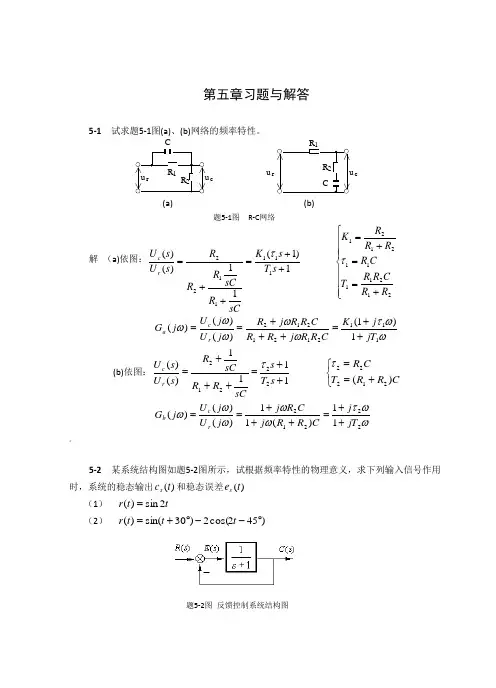
自动控制原理第五章习题及答案

自动控制原理第五章习题及答案

第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。

u r R1u cR2CR2R1u r u c(a) (b)题5-1图R-C网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图：⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++=="5-2某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs和稳态误差)(tes（1）tt r2sin)(=（2）)452cos(2)30sin()(︒--︒+=ttt r题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=-系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ （2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ>)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应 h t e e t tt()..=-+≥--11808049试求系统频率特性。

第5章图与网络分析163页PPT

第5章图与网络分析163页PPT

bi j 0wi j
(vi ,vj)E (vi ,vj)E
例6.4 下图所表示的图可以构造权矩阵B如下:
v1 4
v2
36
72
v6 4
3
3
v3
5
2
v5
v4
v1 0 4 0 6 4 3
v
2

4
0
2
7
0
0

B

v3
0
2
0
5
0
3
v4 6 7 5 0 2 0
v
5
4
17
v4
树与图的最小树
v1 23 v6
20
v2
1
4
v7
9
15 v3
28 25
16 3
v5
17
v4
v1
v2
23 v6
1
4
v7
9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23 v6
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28
25
16 3
v5
17
v4
v1
②
15
9
7 ④ 14
⑤
①
10
19
20
6 ⑥
③
25
图的矩阵描述： 邻接矩阵、关联矩阵、权矩阵等。
1. 邻接矩阵 对于图G=（V，E），| V |=n， | E |=m，有nn阶方矩阵

8.1__图与网络分析基本概念

8.1__图与网络分析基本概念

• 不连通图中的每个连通的部分,称为原图的连通分图. 链、圈、路、回路都是原图的连通分图.
16
5、连通图、连通分图、子图
• 给定图 G
(V , E )
,如果有 (V , E ),使得 V V,E E ， G 为 则称 G 为 G 的一个子图.当 V V 时, 则称 G G 的一个
而 e i 是 v i , v j的关联边. • 同一条边的两个端点称为相邻顶点.具有共同端点的边 称为相邻边. • 一条边的两个端点相同,称为环.具有两个共同端点的
两条边称为多重边. • 既没有环也没有多重边的图称为简单图.
9
3、端点、关联边、相邻、次
• 一个没有环,但允许有多重边的图称为多重图. 今后若不加特别说明,所研究的图均为简单图. • 在无向图中,以顶点 v 为端点的边的数目,称为该顶点 的次,记作 d ( v ) . 次为1的点称为悬挂点,连接悬挂点的边称为悬挂边. 次为0的点称为孤立点. 仅有孤立点的图为零图. 次为奇数的点称为奇点,次为偶数的点称为偶点. 图中顶点均为偶点的图称为偶图.
链中没有重复点和重复边的链称为初等链. • 链 ( v i , v i , v i ) 中,若 v i v i ,则称此链为圈.
1 1 k
1
k
没有重复点和重复边的圈称为初等圈.
14
4、链、圈、路、回路
• 设D是一个有向图, G是它的基础图.若 ( v i , e i , ...., e i , v i )
6
无向图
有向图
混合图
• 图G或D的边数记作 m ( G ) 或 m ( D ) , 顶点个数记作n ( G ) 或 n ( D ) .在不引起混淆情况下,也简记为m , n .

第5章-宽带IP网络

第5章-宽带IP网络
根据预置的一些规则，分类器对进入路由器
的每一个分组进行分类。
（4）队列调度器(Scheduler)
它主要是基于一定的调度算法对分类后的分
5.2.3
网络节点为了适配不同的网络速率及缓冲通
信的突发量，一般都设有排队机制（如图5-1所
图5-1 分组队列调度
（1）传统的先进先出（FIFO）队列
所有分组都进入同一个队列，先到达的分组 先接收服务。
② IP报文标签的产生和分配所需的网络拓扑 和路由信息则是通过现有的IP路由协议获得的， 不用进行2层地址和3层地址之间的转换就可以实 现IP地址和标签之间的映射。
5.5.2 MPLS
目前MPLS实现信令的方式可分为两类，一
类是标签分配协议/约束路由—标签分配协议
（LDP/CR LDP），它支持IP QoS，还考虑了
区分业务是由综合业务(Int-Serv )发展 而来的，它采用了综合业务分类思想，抛 弃了分组流沿路节点上的资源预留。区分 业务区域的主要成员有：核心路由器、边 缘路由器、资源控制器（Bandwidth Broker，BB）。区分业务模型的网络结构 如图5-2所示。
图5-2 区分业务模型网络结构
（4）分级的基于级别的排队(CBQ)
业务被分成不同级别，每种级别又可细分成 若干子级 (Sub-class)。
5.2.4 综合业务模型的优缺点
1
① 能够提供绝对有保证的QoS。
② RSVP在源和目的地间可以使用现有的路 由协议决定流的通路。
③ 设计综合模型开始的目的之一就是使得 QoS能够工作在单播和多播下。
2．QoS
互联网工程部（Internet Engineering Task Force，IETF）已经建议了很多服务模型和机制， 以满足QoS的需求。主要有：综合业务模型、区 分业务模型、多协议标签交换（MPLS）、流量 工程和约束路由。 IETF提出的Integrated Services/RSVP和 Differentiated Services是两种IP网络提供QoS的 模型。

第5章网络消费者行为分析(共36张PPT)

第5章网络消费者行为分析(共36张PPT)
① 兴趣
从心理学的角度讲，兴趣具有很大的动机的成分。社会上 的许多人就是为了兴趣的需求而进行某些活动的。如果有 几种可供人选择的目标可以满足人们的需求，人们总是根 据自己的兴趣决定选择的对象。
2022/9/14
9
② 生理的需求
人类生活的生存的基本要求，如：吃、穿、用、住、行 等。这些需求必须得到最低限度的满足。在传统消费模式 下，首先将满足生理需求的物品放在购买的第一位。对于 网络消费者，这种情况有了较大的变化。能够上网的人多 数已经解决了基本生活用品的购买问题，因此它的注意力 集中往往不是在这一层次的需求中。
到复杂的自我实现的需求；
人的某一级的需求得到最低限度的满足之后，才会追求高一 级的需求。
2022/9/14
5
1．动机
是指推动人进行活动的内部原动力。即激 励人活动的原因。
动机是一种内在的心理状态； 动机不容易被直接观察到或被直接测量到；
动机可以根据人们长期的行为表现加以了解和 归纳。
2022/9/14
15
3.惠顾动机
这是一种集于理智经验和感情之上的， 对特定的网站、图标广告、商品产生特殊 的信任与偏好而重复性、习惯性前往购买 的一种购买动机。回顾动机的形成经历了 人的意志过程。具惠顾动机的消费者，往 往是一个网站的忠实浏览者。他不仅自己 光顾这一站点，而且对众多的网民也具有 较大的宣传和影响功能。
2022/9/14
18
在网络消费中，各个层次的消费不是互相排斥的， 而是紧密联系的，需求之间存在着广泛的交叉现象 。
网络冲浪者大都是具有超前意识的年轻人，他们对新 事物反应灵敏，没有旧框框，接受速度快。虚拟市场 中，最先进的产品和最时髦的商品会以最快的速度与 消费者见面。

运筹学图与网络分析

运筹学图与网络分析
v6
07
含有奇点的连通图中不含欧拉圈，此时，最优的邮递路线是什么呢？
08
求解中国邮路问题的奇偶点图上作业法
奇偶点表上作业法
奇偶点表上作业法 (1)找出奇点(一定为偶数个)，在每两个奇点之间找一条链，在这些链经过的所有边上增加一条边，这样所有的奇点变为偶点，一定存在欧拉圈，但是不一定是路线最短的，所以需要检验和调整。 (2)检验增加的边的权值是否是最小的。 定理3 假设M是使得图G中不含奇点的所有增加边，则M是权值总和为最小的增加边的充分必要条件是： 1)图G中每条边上最多增加一条边； 2)在图G的每个圈上，增加的边的总权值不超过该圈总权值的一半。 如果上述两个条件都满足则已经找到权值最小的欧拉圈 否则转入3) 3)调整增加边。如果1)不满足，则从该条边的增加边中去掉偶数条； 如果2)不满足，则将这个圈上的增加边去掉，将该圈的其余边上添加增 加边，转入(2)
v1
v2
v3
v4
v5
v1
v2
v3
v4
v5
图2
图3
如果在比赛中： A胜E， B胜C， A胜D， C胜A， E胜D， A胜B，
v1
v2
v3
v4
v5
注：本章所研究的图与平面几何中的图不 同，这里我们只关心图有几个点，点与点 之间有无连线，两条线有无公共顶点，点 与线是否有关联，至于连线的方式是直线 还是曲线，点与点的相对位置如何都是无 关紧要的。
求从v1到v8的最短路
(0)
(1,1)
(1,3)
(3,5)
(2,6)
(5,10)
(5,9)
(5,12)
注：在给顶点编号时，如果在多个为标号点均取得最小值Llk则对这多个点同时标号，这些点的第二个标号相同，但是第一个标号不一定相同。

08运筹学-图论

08运筹学-图论
v i 是 边e j的 两 个 端 点 2 当 且 仅 当 m ij 1 当 且 仅 当 v i 是 边e j的 一 个 端 点 0 其 他
3. 权矩阵 对于赋权图G=(V,E), 其中边 (vi , v j )有权 w i ,j 构造矩阵B=(bij) nn 其中：
wi j bi j 0
运 筹 帷 幄 之 中
第八章
决 胜
图与网络分析
Graph Theory and Network Analysis
千 里 之 外
图与网络分析
本章主要内容： 图与网络的基本知识
树和最小支撑树
最短路问题
最大流问题
最小费用流问题
中国邮路问题
§1 图与网络的基本知识
图论起源——哥尼斯堡七桥问题
A
C
A
D
C
B
910201571419256链圈连通图义定义无向图中一个点边交错的序列序列中的第一个和最后一个元素都是点若其中每条边以序列中位于它之前和之后的点为端点则称这个点边序列为图中连接其第一个点与最后一个点的称为无向图中一个点边交错的序列序列中的第一个和最后一个元素都是点若其中每条边以序列中位于它之前和之后的点为端点则称这个点边序列为图中连接其第一个点与最后一个点的称为链
2016/5/30
链，圈，连通图 定义 无向图中一个点、边交错的序列，序列中的第一个和 最后一个元素都是点，若其中每条边以序列中位于它之前和 之后的点为端点，则称这个点边序列为图中连接其第一个点 与最后一个点的称为链。 链中所含的边数称为链长。
{v0 , e1 , v1 ,L , ek , vk }
问题：一个散步者能否从任一 块陆地出发，走过七座桥，且 每座桥只走过一次，最后回到 出发点？ 结论：不能。每个结点关联的 边数要均为偶数。

运筹学复习题-1

运筹学复习题-1

第一章线性规划及单纯形法一、复习思考题1 试述线性规划数学模型的结构及各要素的特征。

2 线性规划的解有哪几种情况。

3 什么是线性规划问题的标准形式，如何将一个非标准型的线性规划问题转化为标准形式。

4 试述线性规划问题的可行解、基解、基可行解、最优解的概念以及上述解之间的相互关系。

5 试述单纯形法的计算步骤，如何在单纯形表上去判别问题是具有惟一最优解、无穷多最优解、无界解或无可行解。

6 如果线性规划的标准型式变换为求目标函数的极小化min z，则用单纯形法计算时如何判别问题已得到最优解。

7 在确定初始可行基时，什么情况下要在约束条件中增添人工变量，在目标函数中人工变量前的系数为(一M)的经济意义是什么。

8 什么是单纯形法计算的两阶段法，为什么要将计算分两个阶段进行，以及如何根据第一阶段的计算结果来判定第二阶段的计算是否需继续进行。

9 简述退化的含义及处理退化的勃兰特规则。

10 举例说明生产和生活中应用线性规划的方面，并对如何应用进行必要描述。

二、判断下列说法是否正确1、图解法同单纯形法虽然求解的形式不同，但从几何上理解，两者是一致的；2、线性规划模型中增加一个约束条件，可行域的范围一般将缩小，减少一个约束条件，可行域的范围一般将扩大；3、线性规划问题的每一个基解对应可行域的一个顶点.4、如线性规划问题有最优解，则最优解一定对应可行域边界上的一个点；5、用单纯形法求解标准型式的线性规划问题时，与＞j对应的变量都可被选作换入变量；6、单纯形法计算中，选取最大正检验数σk 对应的变量xk作为换入变量，将使目标函数值得到最快的增长；7、线性规划问题任一可行解都可以用全部基可行解的线性组合表示；9、对一个有n个变量，m个约束的标准型的线性规划问题，其可行域的顶点恰好为mn C个；10、单纯形法的迭代计算过程是从一个可行解转换到目标函数值更大的另一个可行解；11、若线性规划问题具有可行解，且其可行域有界，则该线性规划问题最多具有有限个数的最优解；12、线形规划可行域的某一项点若其目标函数值优于所有顶点的目标函数值，则该顶点处的目标函数值达到最优。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如：
乙
为了反映城市之间有没有航
班，我们可用右图表示。甲城与 乙城，乙城与丙城有飞机到达， 而甲、丙两城没有直飞航班。
对于工作分配问题，我们可 能用点表示工人与需要完成的工 作，点间连线表示每个工人可以
甲 丙
工人
甲 乙
工作 A
B
胜任哪些工作如右图所示。
丙
C
Ｄ
4
图的定义：
所谓图，就是顶点（简称点）和一些点之间的连线（不带箭头或者 带箭头）所组成的集合。
v v 一条联结
和
i1
in的链，记作
vi1 ,vi2 , 。 ,vin
9
（2）开链和闭链：如果 vi1 ，vi则n 该链称为开链；如果
称为闭链（或称为圈）。
v，i1 =则v该in 链
（3）简单链和初等链：如链内所含的边均不相同，称之为简单链；如 链内所含的点均不相同，称之为初等链。
如：
Ｖ1
e4
有向图D中的链不一定是路，因为有向图的链可能存在和链的方向
（4）基础图和路：若把一个有向图D的方向去掉，即每一弧都用相应 得无向边代替，所得到的一个无向图，称为该有向图D的基础图， 记为G（D）；
基础图G（D）中的链（或圈）恢复无向边的方向后，称为有向图
D的链（或圈）。
若交替序列 vi1 ,ai1 ,vi2 ,ai2 , 是,有vin向-1 ,a图in-G1 ,v的in一条链，且满
Ｖ4
e5
v1,v2 ,v3,v4 ,v5 ,v3,v6 ,v7
是简单链，
v1,v2 ,v3,v6 ,v7
e1 e2
Ｖ2
e7
Ｖ6
e3
Ｖ5 是初等链，
e6
Ｖ3
e9
e8
Ｖ7
v1,v2 ,v3,v4 ,v1
是初等圈，
v4 ,v1,v2 ,v3,v5 ,v7 ,v6 ,v3,v4
是简单圈，
10
6
如有向图：D= V,A
Ｖ3 a2
Ｖ1
a3
a1
Ｖ2
V=v1,v2 ,v3 ,v4 ,v5 ,v6 ,v7
a8
Ｖ5
Ｖ7
a10
A=a1,a2,a3, ,a11
a11
a6 a4
a9 Ｖ6
a7
a1= v1,v2 ,a2 = v1,v3 ,a3= v3,v2 , a4 = v3,v4 ,a5= v2,v4 ,a6= v4,v5 ,
A
置的解题方法”的论文，解决了著名的哥尼斯
堡七桥问题．
C
D
欧拉证明了上述图形一笔划是不可能的，
因为图中每一个点都只和奇数条线相关联．
B
他的结论是：图形能一笔画的充要条件是图形的奇顶点（连接
奇数条线的顶点）的个数为零
3
二、图的定义
在自然界和人类的实际生活中，常用点和点与点之间的联线
所构成的图，来反映某些研究对象和对象之间的某种特定的关系。
（2）端点和关联边：若 e= vi ,vj， 则E称顶点
是e v的i ,v关j 联边。
是 v的i ,v端j 点，e
（3）相邻点和相邻边：若顶点 v和i v与j 同一条边相关联，则称点 和vi
为v j相邻点；若边 和ei 有e一j 个共同的端点，则称其为相邻边。
（4）环和多重边：若边的两个端点属同一顶点，则称该边为环；若两个
V仍表示有向图D的非空的顶点集合，A 表示D的弧集合。一条方向从
指向 vi的弧记v为j
。a= vi,vj
5
如无向图： G=V,E
Ｖ1
e5
Ｖ4
e7
e1
Ｖ2
e2
e6
e3
Ｖ3
e4
V= v1,v2 ,v3,v4 E=e1,e2,e3,e4,e5,e6 ,e7
e1=v1,v2 ,e2 =v1,v2 ,e3=v2,v3 , e4 =v3,v4 ,e5=v1,v4 ,e6=v1,v3 ,e7 =v4,v4
端点之间多于一条边，则称这些边为多重边。
（5）多重图和简单图：含多重边的图称为多重图，无环也无多重边的图 称为简单图。
8
（6）次和孤立点：与点关联的边的条数，称为点的次，记作 d(v；) 次 数为零的点为孤立点。
（7）悬挂点和悬挂边：次为1的点称为悬挂点；悬挂点的关联边称为 悬挂边。
（8）奇点和偶点：次为奇数的点称为奇点；次为偶数的点为偶点。
a5
Ｖ4
a7 = v4,v6 ,a8= v5,v3 , a9= v5,v4 , a10 = v5,v6 a11= v6,v7
7
三、基本概念
点和边的相关概念：
（1）顶点数和边数：给定图 G=V，,E集 合V的元素的个数，称为图G的顶点
数，记作 ；集p(G合) E的元素的个数，称为图G的边数，记作 。 q(G)
第5章 图与网络分析
图论的基本概念 最小支撑树 最短路问题
图论是由瑞士数学家欧拉（Euler）于1736年创始的，当时有一个
世界难题，叫“哥尼斯堡七桥问题” 。
哥尼斯堡城中有一条河，叫普雷格尔河，河中有两个岛，河上有七
座桥，如图所示。当时那里的居民
足
aik =，v即ik链,vi中k+1 每一条弧的箭头方向都和链的方向一致，那么
该链称为有向图D 的一条从 到 的路，v简i1 记vin μ=vi1 ,vi2 , 。,又vi若n-1 ,vin ，则称μ为v图i1 =Dv中in 的回路。
➢ 对无向图G来说，链和路（闭链和回路）这两个概念是一致的。但
热衷于这样的问题：
A
一个散步者能否走过七座桥，
但每座桥只走过一次，最后回到
C
D
出发点。
B
2
欧拉用A、B、C、D四点表 示河的两岸和小岛，用两点间的 联线表示桥，如右下图所示，该 问题可归结为：
能否从某一点出发，一笔画 出这个图形，最后回到出发点而 不重复？即一笔画问题。
A
C
D
B
欧拉在1786年发表了题为“依据几何位
为区别起见，不带箭头的连线称为边， 带箭头的连线称为弧。
➢ 如果一个图是由点和边所构成的，则称之为无向图（也简称为图），
记作 G=V，,E其 中V表示图G的非空的顶点集合，E表示G的边的集合。
连接顶点vi和 v的j 边记为
e；= vi ,v j
➢ 如果一个图是由点和弧所构成的，则称之为有向图，记作 D=V，,A其 中
定理1 图 G=V中,E，所有顶点的次之和等于所有边数的2倍，
即 d(v)=2q vV
链的概念：
（1）给定一个图 G=V，,E一 个点、边的交错序列
vi1 ,ei1 ,vi2 ,ei2 , ,vin-1 ,ein-1 ,vin ，
如果满足 eit = vit ,vit+1 , t=1, 2, n-。1这样的序列称为