第五章数据拟合.

第五章 差值与拟合方法5.4 最小二乘拟合方法5.4.1 线性最小二乘拟合方法设{}m k x 0k )(=φ是一个线性无关的函数系，则称线性组合∑==mk k k a x 0)(φφ为广义多项式。

如三角多项式：∑∑==+=m k k m k k kx b kx a x 00sin cos )(φ设由给定的一组测量数据),(i i y x 和一组正数),,2,1(n i w i =，求一个广义多项式∑==mk k k x a x 0)()(φφ使得目标函数21])([∑=-=n i i i i y x w s φ达到最小，则称函数)(x φ为数据),,2,1)(,(n i y x i i =关于权系数),,2,1(n i w i =的最小二乘拟合函数，由于)(x φ关于待定系数i a 是线性的，故此问题又称为线性最小二乘问题。

注：这里{}mk k x 0)(=φ可根据实际来选择，权系数的选取更是灵活多变的，有时可选取1=i w ,或n w i 1=。

对于n w i 1=，则相应问题称为均方差的极小化问题。

5.4.2 最小二乘拟合函数的求解要使最小二乘拟合问题的目标函数（）达到最小，则由多元函数取得极值的必要条件得),,2,1,0(m k o a s k==∂∂ 即 ),,2,1,(0)(])([0m o k x y x a w i k n i i mk i i k k i ==-∑∑==φφ亦即 ),,2,1,0()(])()([00m k x y w a x x w ni i k j i j m j i k i j i ==∑∑∑==φφφ是未知量为m a a a ,,,,a 110 的线性方程组，称之为正规方程组。

实际中可适当选择函数系{}mk x 0k )(=φ，由正规方程组解出m a a a a ,,,,210 ，于是可得最小二乘拟合函数∑==mk k k x a x 0)()(φφ。

5.4.3 一般线性最小拟合方法将上面一元函数的最小拟合问题推广到多元函数，即为多维线性最小二乘拟问题。

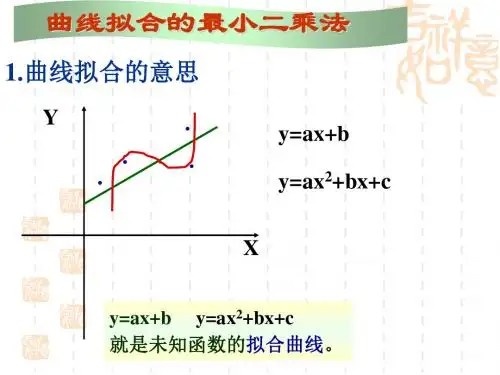
第五章 数据拟合这就是数据拟合成曲线的思想，简称为曲线拟合(fitting a curve)。

根据一组二维数据，即平面上的若干点，要求确定一个一元函数y = f (x )，即曲线，使这些点与曲线总体来说尽量接近，曲线拟合其目的是根据实验获得的数据去建立因变量与自变量之间有效的经验函数关系，为进一步的深入研究提供线索。

本章的目的，掌握一些曲线拟合的基本方法，弄清楚曲线拟合与插值方法之间的区别,学会使用MATLAB 软件进行曲线拟合。

§1 最小二乘法给定平面上的点(x i, y i )，（i = 1,2,…,n ），进行曲线拟合有多种方法，其中最小二乘法是解决曲线拟合最常用的方法。

最小二乘法的原理是：求 ∑∑==-==n i i i ni i y x f x f 1212])([),(δδ使 达到最小如图1所示，其中δi 为点(x i ,y i )与曲线y=f (x )的距离。

曲线拟合的实际含义是寻求一个函数y=f (x )，使f (x )在某种准则下与所有数据点最为接近，即曲线拟合得最好。

最小二乘准则就是使所有散点到曲线的距离平方和最小。

拟合时选用一定的拟合函数f (x ) 形式，设拟合函数可由一些简单的“基函数”（例如幂函数，三角函数等等） )(),...,(),(10x x x m ϕϕϕ来线性表示：)(...)()()(1100x c x c x c x f m m ϕϕϕ+++=图1 曲线拟合示意图现在要确定系数c 0，c 1，…，c m ，使d 达到极小。

为此，将f (x )的表达式代入d 中，d 就成为c 0，c 1，…，c m 的函数，求d 的极小，就可令d 对 c i 的偏导数等于零，于是得到m +1个方程组，从中求解出c i 。

通常取基函数为1，x ，x 2，x 3，…，x m ，这时拟合函数f (x )为多项式函数。

当m =1时，f (x ) = a + bx ，称为一元线性拟合函数，它是曲线拟合最简单的形式。

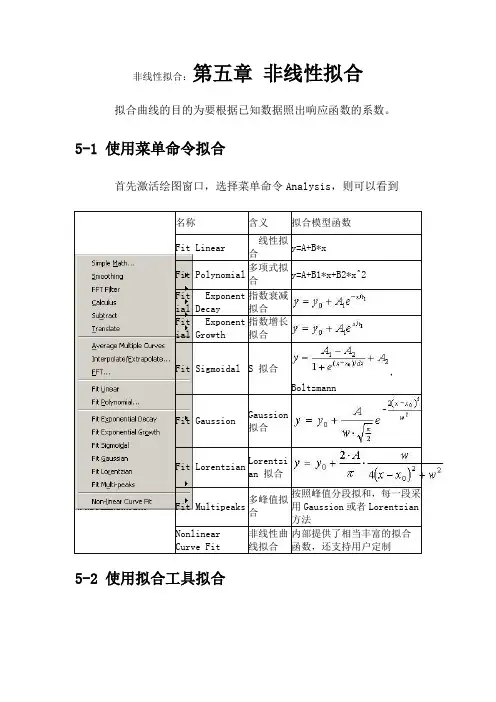
非线性拟合：第五章非线性拟合拟合曲线的目的为要根据已知数据照出响应函数的系数。

5-1 使用菜单命令拟合
首先激活绘图窗口，选择菜单命令Analysis，则可以看到
，
Gaussion
5-2 使用拟合工具拟合
为了给用户提供更大的拟合控制空间，Origin提供了三种拟合工具，即线性拟合工具、多项式拟合工具、S拟和工具。

具体自己去体会。

5-3 非线性最小平方拟合NLSF
这是Origin提供的功能最强大、使用也最复杂的拟合工具。

方法是Analysis-》Non-Linear Curve Fit－》Advanced Fitting Tools或者Fitting Wizad
具体的请自己体会。

高级模式 利用Function-》new 可以自定义拟合函数
基本模式，利用new 可以自定义拟合函数
Wizad模式
高级模式中利用Action－》Dataset设置，在基本模式中用Select
Dataset设置。

数据拟合方法研究之阿布丰王创作中文摘要在我们实际的实验和勘探中,城市发生年夜量的数据.为了解释这些数据或者根据这些数据做出预测、判断,给决策者提供重要的依据.需要对丈量数据进行拟合,寻找一个反映数据变动规律的函数.本文介绍了几种经常使用的数据拟合方法,线性拟合、二次函数拟合、数据的n次多项式拟合等.并着重对曲线拟合进行了研究,介绍了线性与非线性模型的曲线拟合方法,最小二乘法、牛顿迭代法等.在传统的曲线拟合基础上,为了提高曲线拟合精度,本文还研究了多项式的摆动问题,从实践的角度分析了发生这些摆动及偏差的因素和特点,总结了在实践中减小这些偏差的处置方法.采纳最小二乘法使变量转换后所得新变量离均差平方和最小,其实纷歧定能使原响应变量的离均差平方和最小,所以其模型的拟合精度仍有提高的空间.本文以残数法与最小二乘法相结合,采纳非线性最小二乘法来获得拟合效果更好的曲线模型.随着计算机技术的发展,实验数据处置越来越方便.但也提出了新的课题,就是在选择数据处置方法时应该比以往更为慎重.因为稍有失慎,就会非常方便地根据正确的实验数据得出不确切的乃至毛病的结论.所以提高拟合的准确度是非常有需要的关键词：数据拟合、最小二乘法、曲线拟合、多项式摆动、残数法Data Fitting MethodAbstractInourexperimentsand exploration,it will produce large amounts ofdata.In order to explain these data to make predictions based on these data to determine, provide an important basis for policy makers.Need to fit the measured data to find a function toreflect data changes in the law.This article describes several commonly used data fitting methods, and focused on a nonlinear curve fitting of the model.This paper introduces some commonly used data fitting method, linear fitting, secondary function fitting, data n times polynomial fitting etc. TAnd focuses on the curve fitting, introduced the linear and nonlinear model of curve fitting method, the least square method, Newton iterative method, etc. In the traditional curve fitting basis, in order to improve the curve fitting precision, this paper also studies the polynomial swing, from the perspective of the practice the oscillation and deviation of factors and characteristics, and summarizes the decrease in practice the treatment method of thesedeviations. The least square method to variable after converting from new variables are the sum of squared residuals minimum, not necessarily make the original response from all the variables of the sum of squared residuals minimum, so the model fitting precision still has room to improve.Based on the number of residual method and least square method, and the combination of nonlinear least square method to get better fitting effect of curve model.With the development of computer technology, the experiment data processing more and more convenient. But also put forward the new subject, which is in the data processing method of choice should be more careful than ever before.Because carelessly a bit, it can be very easily according to the correct experimental data that not the exactand even the wrong conclusion. Therefore, to raise the fitting accuracy is very necessary Key words：Data Fitting ; Least square method; Curve fitting; Polynomial swing; Residual method目录中文摘要IAbstractII第一章绪论11．1数据简介11.1.1名词解释11.1.2数据属性11.2 曲线拟合简介2第二章数据拟合方法分类32.1 线性拟合52.2 二次函数拟合72.3 数据的n次多项式拟合92.4 点集{x1,x2,……,x m}上的正交多项式系10 2.5 用正交多项式系组成拟合函数的多项式拟合112.6 指数函数的数据拟合122.7 多元线性函数的数据拟合13第三章曲线拟合特性143.1 线性模型的曲线拟合153.1.1 最小二乘法及其计算153.1.2 用正交多项式作最小二乘拟合213.2 非线性模型的曲线拟合253.2.1 牛顿迭代263.2.2 罕见非线性模型26第四章多项式的摆动314.1 多项式摆动介绍324.2 影响多项式拟合偏差的因素344.2.1 实验数据的不均匀性344.2.2 数据的密度354.2.3 拟合曲线的适用区间354.3 使用多项式拟合的注意事项364.3.1尽量防止高阶多项式的拟合364.3.2坚持密度374.3.3在实验数据走向比力明确的前提下,可以考虑其他的非线性拟合方法37第五章残数法与最小二乘法结合385.1 二项指数曲线原理与方法395.2 资料与分析415.3 残数法与最小二乘法结合总结44第六章总结47结束语47参考文献50附录1 英文原文54附录2 中文翻译69附录3 法式83第一章绪论在我们实际的实验和勘探中,城市发生年夜量的数据.为了解释这些数据或者根据这些数据做出预测、判断,给决策者提供重要的依据.需要对丈量数据进行拟合,寻找一个反映数据变动规律的函数.1．1数据简介科学实验、检验、统计等所获得的和用于科学研究、技术设计、查证、决策等的数值.1.1.1名词解释研究数据就是对数据进行收集、分类、录入、贮存、统计分析,统计检验等一系列活动的统称.1.1.2数据属性柯岩《奇异的书简·船主》：“贝汉廷分析着各个分歧的数据,寻找着规律,终于抓住了矛盾的牛鼻子.”数据是载荷或记录信息的按一定例则排列组合的物理符号.可以是数字、文字、图像,也可以是计算机代码.对信息的接收始于对数据的接收,对信息的获取只能通过对数据布景的解读.数据布景是接收者针对特定命据的信息准备,即当接收者了解物理符号序列的规律,并知道每个符号和符号组合的指向性目标或含义时,即可以获得一组数据所载荷的信息.亦即数据转化为信息,可以用公式“数据+布景=信息”暗示.数据拟合在很多处所都有应用,主要用来处置实验或观测的原始离散数据.通过拟合可以更好的分析和解释数据.1.2 曲线拟合简介曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的暗示方式.科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望获得一个连续的函数（也就是曲线）或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合.在科学实验或社会活动中,人们经常需要观测很大都据的规律,通过实验或者观测获得量x与y的一组数据对（）(i=1,2, …,N),其中是彼此分歧的.人们希望用一类与数据实质规律相适应的解析表达式,来反映量x与y之间的依赖关系,即在一定意义下“最佳”地迫近或拟合已知数据.常称作拟合模型,当c在中线性呈现时,称为线性模型,否者称为非线性模型.线性模型是回归模型中最罕见的一种,但在实际中,许多现象之间的关系往往其实不是线性的,而是呈现某种曲线关系.如服药后血药浓度与时间的关系；病毒剂量与致死率的关系；化学反应的反应物浓度与反应速度的关系.这就发生的曲线拟合,用连续曲线近似地刻画或比力平面上离散点组所暗示的坐标之间的函数关系.用解析表达式迫近离散数据的一种方法.第二章数据拟合方法分类在实验中,实验和戡测经常会发生年夜量的数据.为了解释这些数据或者根据这些数据做出预测、判断,给决策者提供重要的依据.需要对丈量数据进行拟合,寻找一个反映数据变动规律的函数.数据拟合方法与数据插值方法分歧,它所处置的数据量年夜而且不能保证每一个数据没有误差,所以要求一个函数严格通过每一个数据点是分歧理的.数据拟合方法求拟合函数,插值方法求插值函数.这两类函数最年夜的分歧之处是,对拟合函数不要求它通过所给的数据点,而插值函数则必需通过每一个数据点.例如,在某化学反应中,测得生成物的质量浓度y (10–3 g/cm3)与时间t （min）的关系如表所示显然,连续函数关系y(t) Array是客观存在的.可是通过表中的数据不成能确切地获得这种关系.何况,由于仪器和环境的影响,丈量数据难免有误差.因此只能寻求一个近拟表达式y = ϕ(t)寻求合理的近拟表达式,以反映数据变动的规律,这种方法就是数据拟合方法.数据拟合需要解决两个问题：第一,选择什么类型的ϕ作为拟合函数（数学模型）；第二,对选定的拟合函数,函数)(t如何确定拟合函数中的参数.数学模型应建立在合理假设的基础上,假设的合理性首先体现在选择某种类型的拟合函数使之符合数据变动的趋势（总体的变动规律）.拟合函数的选择比力灵活,可以选择线性函数、多项式函数、指数函数、三角函数或其它函数,这应根据数据分布的趋势作出选择.为了问题叙述的方便,将例1的数据表写成一般的形式2.1 线性拟合假设拟合函数是线性函数,即拟合函数的图形是一条平面上的直线.而表中的数据点未能精确地落在一条直线上的原因是实验数据的误差.则下一步是确定函数y= a + b x中系数a 和b 各即是几多？从几何布景来考虑,就是要以a 和b 作为待定系数,确定一条平面直线使得表中数据所对应的10个点尽可能地靠近这条直线.一般来讲,数据点将不会全部落在这条直线上,如果第k 个点的数据恰好落在这条直线上,则这个点的坐标满足直线的方程,即a +b x k = y k如果这个点不在直线上,则它的坐标不满足直线方程,有一个绝对值为k k y bx a -+的不同（残差）.于是全部点处的总误差是∑=-+101k k ky bxa这是关于a 和b 的一个二元函数,合理的做法是选取a 和b ,使得这个函数取极小值.可是在实际求解问题时为了把持上的方便,经常是求a 和b 使得函数∑=-+=1012)(),(k k k y bx a b a F到达极小.为了求该函数的极小值点,令0=∂∂a F ,0=∂∂bF, 得0)(2101=-+∑=k k ky bxa , ∑==-+1010)(2k k k k x y bx a这是关于未知数a 和b 的线性方程组.它们被称为法方程,又可以写成⎪⎪⎩⎪⎪⎨⎧=+=+∑∑∑∑∑=====101101210110110110k k k k k k k k k k k y x b x a x y b x a 求解这个二元线性方程组便得待定系数a 和b ,从而得线性拟合函数2.2 二次函数拟合假设拟合函数不是线性函数,而是一个二次多项式函数.即拟合函数的图形是一条平面上的抛物线,而表中的数据点未能精确地落在这条抛物线上的原因是实验数据的误差.则下一步是确定函数y = a 0 + a 1 x + a 2 x 2中系数a 0、a 1和a 2各即是几多？从几何布景来考虑,就是要以a 0、a 1和a 2为待定系数,确定二次曲线使得表中数据所对应的10个点尽可能地靠近这条曲线.一般来讲,数据点将不会全部落在这条曲线上,如果第k 个点的数据恰好落在曲线上,则这个点的坐标满足二次曲线的方程,即a 0 + a 1 x k + a 2 x k 2 = y k如果这个点不在曲线上,则它的坐标不满足曲线方程,有一个误差（残差）.于是全部点处的总误差用残差平方和暗示∑=-++=10122210210])[(),,(k k k k y x a x a a a a a F这是关于a 0、a 1和a 2的一个三元函数,合理的做法是选取a 0、a 1和a 2,使得这个函数取极小值.为了求该函数的极小值点,令00=∂∂a F ,01=∂∂a F ,02=∂∂a F得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-++=-++=-++∑∑∑===10122210101221010122100])[(20])[(20])[(2k k k k k k k k k k k k k k x y x a x a a x y x a x a a y x a x a a 这是关于待定系数a 0、a 1和a 2的线性方程组,写成等价的形式为⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++∑∑∑∑∑∑∑∑∑∑∑===========101210124101131010210110110123121010101101221101010k kk k k k k k k k k k k k k k k k k kk k k k y x a x a x a x y x a x a x a x y a x a x a这就是法方程,求解这一方程组可得二次拟合函数中的三个待定系数.下图反映了例题所给数据的二次曲线拟合的结果2.3数据的n 次多项式拟合已知函数在个离散点处的函数值,假设拟合函数是n 次多项式,则需要用所给数据来确定下面的函数y = a 0 + a 1 x + a 2 x 2+…… + a n x n这里要做一个假设,即多项式的阶数n 应小于题目所给数据的数目m （例题中m = 10）.类似前面的推导,可得数据的n 次多项式拟合中拟合函数的系数应满足的正规方程组如下⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑=====+==+====m k k n k mk k k mk k n mk nk mk n kmk n k mk n k mk km k kmk n k mk k y x y x ya a a x xx x xxx x m 11110121111112111从这一方程组可以看出,线性拟合方法和二次拟合方法是多项式拟合的特殊情况.从算法上看,数据最小二乘拟合的多项式方法是解一个超定方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++m n m n m m nn n n yx a x a x a a y x a x a x a a y x a x a x a a 22102222221*********( m > n ) 的最小二乘解.而多项式拟合所引出的正规方程组恰好是用超定方程组的系数矩阵的转置矩阵去左乘超定方程组左、右两端所得.正规方程组的系数矩阵是一个病态矩阵,这类方程组被称为病态方程组.当系数矩阵或者是右端向量有微小的误差时,可能引起方程组准确解有很年夜的误差.为了防止求解这样的线性方程组,在做多项式拟合时可以将多项式中的各次幂函数做正交化变换,使得所推出的正规方程的系数矩阵是对角矩阵.2.4 点集{x 1,x 2,……,x m }上的正交多项式系多项式q 0(x ),q 1(x ),q 2(x ),……,q n (x )在点集{x 1,x 2,……,x m }上的正交 ∑==mi i j i k j k x q x q q q 1)()(),(正交多项式系可以认为是幂函数系：1,x ,x 2,……,x n 通过正交变换而获得的一组函数.正交多项式系构造的方法如下：q 0(x )=1,q 0(x ) =x – a 1,(a 1 = n x mi i /1∑=),q k (x ) = (x - a k ) q k -1(x ) - b k q k-2(x ) ,( k = 2,3,……,n ) 其中,∑∑=-=-----==mi i k mi i k i k k k k k x q x q x q q q xq a 1211211111)(/)(),/(),(∑∑=-=-----==mi i k mi i k k k k k k x q x q q q q q b 1221212211)(/)(),/(),(2.5用正交多项式系组成拟合函数的多项式拟合考虑拟合函数：)()()()(1100x q a x q a x q a x n n +++= ϕ,将数据表中的数据代入,得超定方程⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++mm n n m m m n n n n y x q a x q a x q a x q a y x q a x q a x q a x q a y x q a x q a x q a x q a )()()()()()()()()()()()(2211002222221120011122111100 （m > n ） 其系数矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡)()()()()()()()()()()()(21022221201121110m n m m mn n x q x q x q x q x q x q x q x q x q x q x q x q由于多项式q 0(x ),q 1(x ),q 2(x ),……,q n (x )在点集{x 1,x 2,……,x m }上的正交,所以超定方程组的系数矩阵中分歧列的列向量是相互正交的向量组.于是用这一矩阵的转置矩阵去左乘超定方程组左、右两端得正规方程组⎪⎪⎩⎪⎪⎨⎧===),(),(),(),(),(),(11110000y q a q q y q a q q y q a q q n n n n => ⎪⎪⎩⎪⎪⎨⎧===),/(),(),/(),(),/(),(11110000n n n n q q y q a q q y q a q q y q a 其中,∑==m i i k k k x q q q 12)(),(,∑==mi i i k k y x q y q 1)(),(.因为正规方程组中每一个方程都是一元一次方程可以直接写出原超方程组的最小二乘解,所以拟合函数为)(),(),()(),(),()(),(),()(11110000x q q q y q x q q q y q x q q q y q x n n n n +++=ϕ这一结果与用次多项式拟合所得结果在理论是完全一样的,只是形式上分歧、算法实现上防止了解病态方程组.2.6 指数函数的数据拟合问题1：世界人中预测问题下表给出了本世纪六十年代世界人口的统计数据(单元：亿)有人根据表中数据,预测公元2000年世界人口会超越 60亿.这一结论在六十年代末令人难以置信,但现在已成为事实.试建立数学模型并根据表中数据推算出2000年世界人口的数量.根据马尔萨斯人口理论,人口数量按指数递增的规律发展.记人口数为 N (t ),则有指数函数N e a bt =+.现需要根据六十年代的人口数据确定函数表达式中两个常数a、b.为了计算方便,对表达式两边取对数,得ln N a bt=+,令Ny ln=.于是btaty+=)(.(1)计算出表中人口数据的对数值y k = ln N k ( k = 1,2, (9)(2) 根据表中数据写出关于两个未知数a 、b的9个方程的超定方程组（方程数多于未知数个数的方程组）a +b tk = yk( k = 1,2, (9)其中,t1 =1960,t2 =1961,t3 =1962,……,t9 =1968；y1= ln29.72,y2 = ln 30.61,……,y9 = ln34.83.(3) 利用MATLAB解线性方程组Ax=c的命令A\c计算出a 、b的值,并写出人口增长函数.利用人口增长函数计算出2000年世界人口数据：N(2000)2.7 多元线性函数的数据拟合问题2 人的耗氧能力的数据拟合.人的耗氧能力y (ml/min·kg)与下列变量有关x1年龄x2体重x31.5英里跑步所用时间x4静止时心速x5跑步时最年夜心速某健身中心对31个自愿者进行测试,获得31组数据（每一组数据有6个数）令耗氧能力为因变量,其它的指标为自变量,建立线性模型为了确定6个系数,利用已记录的数据得超定方程组这一方程组包括6个未知数,但却有31个方程.写出超定方程组的系数矩阵和右端向量如下⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=31,531,431,331,231,152423222125141312111111x x x x x x x x x x x x x x x A,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=3121y y y y 由最小二乘法可得正规方程组y A AX A T T =其中,T第三章 曲线拟合特性在科学实验或社会活动中,人们经常需要观测很大都据的规律,通过实验或者观测获得量x 与y 的一组数据对（）(i=1,2, …,N),其中是彼此分歧的.人们希望用一类与数据实质规律相适应的解析表达式,来反映量x与y之间的依赖关系,即在一定意义下“最佳”地迫近或拟合已知数据.常称作拟合模型,当c在中线性呈现时,称为线性模型,否者称为非线性模型.3.1 线性模型的曲线拟合已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1, λ2,…,λm), 使得该函数与已知点集的分歧(最小二乘意义)最小.如果待定函数是线性,就叫线性拟合.下面介绍计算线性拟合的基本方法.3.1.1最小二乘法及其计算在函数的最佳平方迫近中,如果只在一组离散点集{}上给出,这就是科学实验中罕见的实验数据{}的曲线拟合,这里,要求一个函数与所给数据{}拟合,若记,设是C[a,b]上线性无关函数族,在中找一个函数,使误差平方和这里这就是一般的最小二乘迫近,用几何语言说,就称为曲线拟合的最小二乘法.用最小二乘法求曲线时,首先要确定的形式.这部纯真三数学问题,还与所研究问题的运动规律及所得观测数据有关；通常要从问题的运动规律或给定命据描图,确定的形式,并通过实际计算选出较好的结果.的一般表达式为（3.2）式暗示的线性形式.若是k次多项式,就是n次多项式.为了使问题的提法更有一般性,通常在最小二乘法中都考虑为加权平方和这里是[a,b]上的权函数,它暗示分歧点处的数据比重分歧,用最小二乘法求拟合曲线的问题,就是在形如(2.2)式的中求一函数,使(3.3)式取得最小.它转化为求多元函数的极小点的问题.由求多元函数极值的需要条件,有若记上式可改写为线性方程组（3.6）称为法方程,可将其写成矩阵形式其中要使法方程（3.6）有唯一解,就要求矩阵G非奇异.必需指出,在[a,b]上线性无关不能推出矩阵G非奇异.例如,令,显然在[]上线性无关,但如果取点,那么有,由此得出为保证方程组（3.6）的系数矩阵G非奇异,必需加上另外的条件.如果函数族在有限点集中的任意n+1(n)个点上都有则称函数族在点集X上满足哈尔条件.这个界说实际上等价于：函数族的任意线性组合在点集X上至多有n个分歧的零点.显然在任意个点上满足哈尔条件.可以证明,如果在上满足哈尔条件,则法方程（3.6）的系数矩阵（2.7）非奇异,于是方程组（3.6）存在唯一的解.从而可以获得函数的最小二乘解为可以证明这样获得的,对任何形如（3.2）式的,都有故确是所求最小二乘解.给定的离散数据,要确定是困难的,一般可取,但这样做那时,与连续情形一样求解法方程（3.6）时将呈现系数矩阵G病态的问题,通常对的简单情形都可通过求法方程（3.6）获得.有时根据给定命据图形,其拟合函数概况上不是（3.2）式的形式,但通过变换仍可化为线性模型.例如,若两边取对数得它就是形如（3.2）式的线性模型.例设数据由下表给出表2-1i 0 1 2 3 41.00 1.25 1.50 1.752.005.10 5.796.537.458.451.629 1.756 1.8762.008 2.135 解根据给定命据描图根据拟合图形可以看出它不是线性形式,因为,可以获得数学模型为,用最小二乘法来确定未知数.两边取对数得,若令,则得.为确定A,b,先将转化为,数据表见2-1.根据最小二乘法,去,得故由法方程解得.于是得最小二乘拟合曲线为现在很大都学软件配有自动选择数学模型的法式,其方法与本例相同.法式中因变量与自变量变换的函数类型较多,通过计算比力误差找到拟合得比力好的曲线,最后输出曲线图形及数学表达式.3.1.2 用正交多项式作最小二乘拟合用最小二乘法获得的法方程（3.6）,其系数矩阵G是病态的,但如果是关于点集带权正交的函数族,即则法方程（2.6）的解为且平方误差为现在我们根据给定节点及权函数,造出带权正交的多项式,注意,用递推公司暗示,即这里是首项系数为1的k次多项式,根据的正交性,得下面用归纳法证明这样给出的是正交的,由（3.10）式第二次及（3.11）式中的表达式,有现假定对及均成立,要证对均成立.由（3.10）式有由归纳法假定时,另外,是首项系数为1的s+1次多项式,它可由的线性组合暗示,而,故由归纳法假定又有于是由（3.12）式,那时.再看由假定有利用（3.11）式中表达式及以上结果,得最后,由（3.11）式有至此已证明了由（3.10）式及（3.11）式确定的多项式组成一个关于点集的正交系.用正交多项式的线性组合作最小二乘曲线拟合,只要根据公司（3.10）及（3.11）逐步求的同时,相应计算出系数并逐步把累加到S()中去,最后就可获得所求的拟合曲线这里n可事先给定或在计算过程中根据误差确定.用这种方法编法式不用解线性方程组,只用递推公式,而且当迫近次数增加一次时,只要把法式中循环数加1,其余不用改变.这就是目前用多项式作曲线拟合最后的计算方法.3.2 非线性模型的曲线拟合以后研究的非线性模型主要是指参数或自变量是非线性的,形式复杂多样,罕见的有多项式形式、双曲线形式、对数形式、幂函数形式等等,更复杂的有修正指数曲线、Compterz曲线以及Logistic 曲线等.如何根据数据的年夜致规律来选择合适的模型,是拟合的关键.总的来说有两中可参考的方法：一是根据散点图来确定类型,即由散点图的形状年夜体确定模型类型；二是根据专业知识和经验,判断研究的数据曲线属于什么类型.现在研究非线性模型的方法用得最多的就是最小二乘法.3.2.1 牛顿迭代无论采用什么方式变换都不成能实现线性化,这样的模型称为不成线性化模型.对不成线性化模型,一般采纳高斯一牛顿迭代法进行参数估计,即借助于泰勒级数展开式进行逐次的线性近似估计.第一步：做Logit-Ln 线性回归,求, , x 和p 的初值.此时x 不能为0值,若输入的x 有0值,则将其设为一小值（例如：0.00001）.首选将原方程变形为如下线性形式：x p x p y A A y ln ln ln 010-=⎪⎪⎭⎫ ⎝⎛+- 将初值设为输入的y 值的最年夜值加1,的初值设为输入的y 值的最小值减0.1.通过简单的直线拟合即可求出p 和的初值.第二步：对Logistic 方程四个参数求偏微分,获得y 对给定系数的增量（△, △, △x, △p ）的泰勒级数展开式.px x A y ⎪⎪⎭⎫ ⎝⎛+=∂∂0111px x A y⎪⎪⎭⎫ ⎝⎛+-=∂∂02111pp xx x x A A x px y ⎪⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=∂∂02001001 2001001ln ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=∂∂p px x A A x x x x p y泰勒级数展开式为：)(0000110p pyx x y A A y A A y y y ∆∂∂+∆∂∂+∆∂∂+∆∂∂+= 由此,将曲线回归转化为多元线性回归,通过迭代计算,获得四个参数的变量△, △, △x, △p,逐步修正四参数的值.多元线性回归与多项式拟合方法相同.每一次迭代可计算出参数变量值,新的参数值为原参数值与变量值的叠加.第三步：为保证迭代收敛,在计算相关系数时,引入一系数a,初值设为2,将a 与参数的变量矩阵相乘,计算相关系数.a=a/2,循环10次,每次a 的值减半.取循环中获得的相关系数最年夜的变量矩阵[△, △, △x, △p].第四步：默认总的迭代次数为1000次,或者当相关系数不再减小时,则迭代停止.返回获得的四参数值.3.2.2 罕见非线性模型对解释变量是非线性的,但参数之间是线性的模型,可以利用变量直接代换的方法将模型线性化,通过线性拟合来计算. 1.多项式函数模型多项式函数形式 令原模型可化为线性形式即可利用多元线性回归分析的方法处置了.这类模型广泛地用于生产和本钱函数.例如总本钱函数可暗示为： 其中,y 暗示总本钱,暗示产出. 2．双曲线模型 双曲线函数形式 3.双对数函数模型函数形式 2k 012k y=+++...+x x x uββββ+212,,kk z x z x z x ===23i 01i 2i 3i y =+++x x x ββββ011y u xββ=++01ln ln y x uββ=++所以弹性为一常数.它暗示x 变动1%,y 变动 了.由于这个特殊的性质,双对数模型又称为不变弹性模型. 4.半对数函数模型函数形式 对线性-对数模型它暗示x 变动1%,y 将变动个单元的绝对量.即y 的绝对变动量即是乘以x 的相对变动量. 5.逻辑斯蒂（Logistic ）曲线函数形式 令 则有 6.指数曲线函数形式 两边取对数得： *1*（ln )/(ln )/dy d y y y Edx d x x xβ∆====∆1%β01ln y x uββ=++ln y x uββ=++ln y x uββ=++1*(ln )/dy dy y dx d x x xβ∆===∆1xy xβ∆∆=1β1βx be a y -+=1yy 1='xe x -='x b a y '+='x ab y =loglog log y a x b=+令则有 7.幂函数曲线 函数形式 两边取对数得：令 则有8.龚伯兹（Gompertz ）曲线函数形式两边取对数得： 令 则有y y '=log a a '=log b b '=log y a b x '''=+bdx y=xb d y log log log +=y y log ='xx log ='da log =y a bx ''=+bxde y =bx d y +=ln ln yy ln ='da ln =y a bx ''=+第四章多项式的摆动在实验科学中,经常会遇到这样的问题,用一组给定的非线性实验数据得出指导性的经验公式,即自变量x与因变量y的函数关系,这就是曲线拟合.在曲线拟合中最小二乘法多项式拟合的应用非常普遍,在许多科学文献中,实验结果都以多项式的形式给出以供参考.虽然多项式的拟合适用普遍,通过适当的拟合多项式的阶数改善曲线迫近实验数据点的水平,但同时也带来晦气的一面.提高拟合多项式的阶数,曲线在某些区间往往会发生非期望的起伏,这使得曲线的参考价值年夜打折扣.。