浅析散布图法

目录摘要 (1)一、简介 (2)（一）两张关系 (2)（二）散布图的基本形式 (3)二、作法 (4)三、用途 (4)四、分类 (4)（1）强正相关（完全正线性相关） (4)（2）弱正相关 (5)（3）无关 (5)（4）弱负相关 (6)（5）强负相关（完全负线性相关） (6)（6）非线性相关 (7)五、绘制程序 (7)六、应用关系 (8)七、构成 (9)八、特色 (9)九、注意事项 (9)十、使用事项 (10)十一：示例，作出放电恢复与放电后电压的散点图 (10)散布图[摘要]质量管理发展到现在已经十分丰富，直方图在质量管理中的运用更为丰富和完善。

统计技术是质量管理中进行质量分析、质量控制和质量改进的基本工具和方法，不使用统计技术难以进行数据分析，在质量管理中直方图是一种常见的统计技术。

直方图作为数字资料统计工具和技术在质量管理中起着至关重要的作用。

[关键词]质量管理统计技术直方图。

一、简介散布图: 散布图是用非数学的方式来辨认某现象的测量值与可能原因因素之间的关系. 这种图示方式具有快捷, 易于交流, 和易于理解的特点. 用来绘制散布图的数据必须是成对的(X,Y). 通常用垂直轴表示现象测量值Y , 用水平轴表示可能有关系的原因因素X. 推荐两轴的交点采用两个数据集(现象测量值集, 原因因素集)的平均值. 收集现象测量值时要排除其他可能影响该现象的因素. 例如, 测量机器制产品的表面品质时,也要考虑到其它可能影响表面品质的因素, 如进给速度, 刀具状态等。

散布图又叫相关图，它是将两个可能相关的变数资料用点画在坐标图上，用成对的资料之间是否有相关性。

这种成对的资料或许是特性--原因，特性--特性--原因的关系。

通过对其观察分析，来判断两个变数之间的相关关系。

这种生产中也是常见的，例如热处理时淬火温度与工件硬度之间的关系，某种元素在材料中的含量与材料强度的关系等。

这种关系虽然存在，但又难以用精确的公式或函数，在这种情况下用相关图来分析就是很方便的。

散布图法-详解散布图法（Scatter Diagram Method）目录• 1 什么是散布图法• 2 散布图法的步骤• 3 散布图法示例什么是散布图法散布图法（Scatter Diagram Method）是指根据若干时期的历史资料，将其业务量和成本数据逐一在坐标图上标注，形成若干个散布点，再通过目测的方法尽可能画出一条接近所有坐标点的直线，并据以推算出固定成本总额和单位变动成本的一种成本习性分析方法。

散布图法由于将全部成本数据均作为描述成本习性的依据，其准确程度比高低点法高。

但因为其采用目测的方法得出固定成本，因而计算结果也具有一定的不准确性。

在质量管理过程中，经常需要对一些重要因家进行分析和控制这些因素大多错综复杂地交织在一起，它们既相互联系又相互制约既可能存在很强的相关性，也可能不存在相关性。

如何对这些因素进行分析？散布团法便是这样一种直观而有效的好方法，通过做散布图，因素之间繁杂的数据就变成了坐标图上的点，其相关关系使一目了然地呈现出来。

在分析质量事故时，总是希望能够寻找到造成质量事故的主要原因，但影响产品质量的因素往往很多，有时只需要分析具体两个因索之间到底存在着什么关系。

这时可将这两种因素有关的数据列出来，并用一系列点标在直角坐标系上，制作成图形，以观察两种因素之间的关系，这种图就称为散布图，对它进行分析称为相关分析。

散布图法的步骤散布图法的工作步骤为：1）收集历史数据收集以前各期产量与总成本的历史数据。

2）画出散布图将各期总成本数据标入直角坐标系，画出散布图。

3）确定固定成本平均值根据离散的历史成本点目测成本随产量变动的趋势，画出一条能反映成本平均变动趋势的直线，直线与纵轴的交点即固定成本平均值。

4）计算单位变动成本在直线上任取一点，根据的计算公式，计算出单位变动成本。

5）计算总成本按照计算出的固定成本平均值（a）、单位变动成本(b)，预测未来某期产量下的总成本，预测公式为：y = a + bx式中:y—未来预测期的总成本；x—产量。

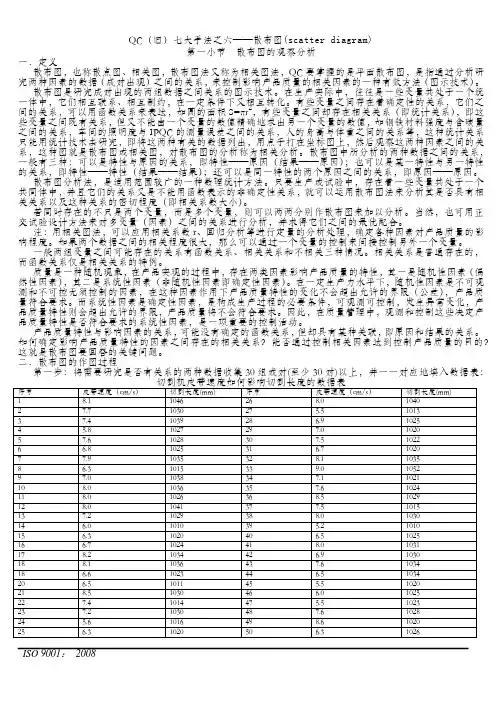
QC（旧）七大手法之六——散布图(scatter diagram)第一小节散布图的观察分析一．定义散布图，也称散点图、相关图，散布图法又称为相关图法，QC要掌握的是平面散布图，是指通过分析研究两种因素的数据（成对出现）之间的关系，来控制影响产品质量的相关因素的一种有效方法（图示技术）。

散布图是研究成对出现的两组数据之间关系的图示技术。

在生产实际中，往往是一些变量共处于一个统一体中，它们相互联系、相互制约，在一定条件下又相互转化。

有些变量之间存在着确定性的关系，它们之间的关系，可以用函数关系来表达，如圆的面积S=πr2，有些变量之间却存在相关关系（即统计关系），即这些变量之间既有关系，但又不能由一个变量的数值精确地求出另一个变量的数值，如钢铁材料强度与含碳量之间的关系，车间的照明度与IPQC的测量误差之间的关系，人的身高与体重之间的关系等，这种统计关系只能用统计技术去研究，即将这两种有关的数据列出，用点子打在坐标图上，然后观察这两种因素之间的关系，这种图就是散布图或相关图，对散布图的分析称为相关分析。

散布图中所分析的两种数据之间的关系，一般有三种：可以是特性与原因的关系，即特性——原因（结果——原因）；也可以是某一特性与另一特性的关系，即特性——特性（结果——结果）；还可以是同一特性的两个原因之间的关系，即原因——原因。

散布图分析法，是适用范围较广的一种数理统计方法。

只要生产或试验中，存在着一些变量共处于一个共同体中，并且它们的关系又是不能用函数表示的非确定性关系，就可以运用散布图法来分析其是否具有相关关系以及这种关系的密切程度（即相关系数大小）。

若同时存在的不只是两个变量，而是多个变量，则可以两两分别作散布图来加以分析。

当然，也可用正交试验设计方法来对多变量（因素）之间的关系进行分析，并求得它们之间的最优配合。

注：用相关图法，可以应用相关系数r、回归分析等进行定量的分析处理，确定各种因素对产品质量的影响程度。

第九章散布图法一什么是散布图散布图也叫相关图它是用来研究判断两个变量之间相关关系的图我们经常会遇到这样一类问题两个变量之间是否有互相联系互相影响的关系如果存在关系那么这种关系是什么样的关系例如某些食品的水分含量与霉变热处理工艺中淬火温度与淬火硬度酿酒中酒药量与出酒率等等在对两个变量进行分析后可以得出有无关系什么样的关系以及二者之间所存在的相互间关系的规律的结论一两种不同的关系当我们分析研究两个有关系的变量问题时常有两种不同的关系1确定性的函数关系这种关系是两个变量之间存在着完全确定的函数关系例如圆的周长C和圆的直径D之间存在着C=D的关系只要知道圆的直径就能精确地求出圆的周长或者知道圆的周长就可求得圆的直径不管谁来计算答案是唯一的这种变量间的关系是完全确定的关系2非确定性的相关关系这种关系是非确定性的依赖或制约的关系例如儿童的年龄和体重之间虽有一定关系但只能一般地说儿童年龄越大体重也越重然而并不是所有的同龄儿童体重都相同在一些生活顾问手册中常可以见到用这样一个公式来表示儿童的年龄和体重之间的关系儿童体重=年龄2+7千克这是一个统计了很多中国儿童年龄和体重的数据后得到的推荐式虽然不是所有2周岁儿童的体重都是11千克但总是在11千克左右我们把这种关系叫相关关系相关关系是可以借助统计技术来描述这种变量之间的关系散布图法就是解决这个问题的统计技术一散布图的基本形式散布图由一个纵坐标一个横坐标很多散布的点子组成图12一1是某零件在热处理中淬火温度与淬火硬度两个变量之间关系的散布图从散布图上的点子分布状况可以观察分析出两个变量x y之间是否有相关关系以及关系的密切程度如何在质量管理活动中我们可以运用散布图来判断各种因素对产品质量特性有响及影响程度的大当两个变量相关程度很大时则找出他们的关系式无影小y=ax+b然后借助于这一关系式只需观察其中一个变量就可以推断出另一个变量以达到简化和节约的目的还可以从控制一个变量估计另一个变量的数值二散布图的作图方法 明散布图的作图步骤举一个酒厂的实例来说一搜集数据某酒厂为要判定中间产品酒醅中酸度含量和酒度两变量之间有无关系以及存在什么关系使用了散布图法会导致判断不准确数据太多计算的工作量就太大 作散布图的数据一般应搜集30组以上数据太少相关就不太明显因而本例搜集了30组酒醅中酸度和对应酒度的数据填入数据表把酸度定为自变量值x 对应的酒度定为应变量y 值表12一1二打 点 先画纵坐标再画坐横标横坐标为自变量取值范围应包括自变量数值x 值的最大值与最小值越往右取越值大本例中x 值最小为0.5最大为1.6则横.4坐标值从0取到1.8为宜纵坐标为应变量应包括应变量数值Y 值的最大值与最小值越往上取值越大本例中Y 值最小是3.4最大是6.8则纵坐标值从3.0取到7.0为宜把数据表中的各组对应数据一一按坐标位置用坐标点表示出来如果碰上一组数据和另一组完全相同本例的第3 组和第30组数据完全相同则在点上加一个圈表示重复☉,如碰上三组数据相同则加上两重圈表示☉把本例30组数据都打上点后就得到图12一2. 三散布图的判断分析散布图的判断分析方法有两种一对照典型图例法3把画出的散布图与典这是最简单的方法图12一是六种典型散布图例型图个关例对照就可得出两变量之间是否相关及属哪一种相的结论把上述例子与典型图例对照就可以得出酸度与酒度呈负相关的结论二简单象限法以图12一2为例1在图上画一条与Y轴平行的P线使P线的左右两侧的点数相等或大致相等本例各为15个点2在图上再画一条与x轴平行的Q使Q线上下两侧的点数相等或大致相等本例Q线通过两个点两侧各14个点3P Q两线把图形分成四个象限区域分别计数各象限区域内的点数(线上的点不计)得n1=0n2=14n3=1n4=134分别计算对角象限区域内数的点n1+n n2+n4本例为n1+n3=0+1=1+n2n4=14+13=27当n1+n3> n2+n4时为正相关当n1+n3< n2+n4时为负相关应该说明的是用打作图的方再点法进行相关分析是最简单的方法由于分析较为粗糙难以在生产实践中应用当需要进行课题研究时必须应用计可进一步找出变量之间内在联系算的方法比较精确地计算出相关关系还的即回归分析法四散布图法在应用中应注意的事项性的数据分层作图否则将会导致不真实的判断结论1应将不同质2散布图相关性规律的适用范围一般局限于观测值数据的范围内不能任意扩大相关判断范图散布图中出现的个别偏离分布趋势的异常点应在查明原因后予以剔除散布图中出现的个别偏离分布趋势的异常点,应在查明原因后予以剔除.。

医院品管圈七大手法之二散布图在医院品管圈开展活动中，七大手法的应用直接影响到医院品管圈项目所取得的效果。

本文主要介绍最常用的手法之二—散布图。

散布图能够准确分析出医院运营中出现问题的原因。

一什么是散布图(WHAT）散布图（Scatter diagram）就是把互相有关联的对应数据，在方格纸上以纵轴表示结果，横轴表示原因，然后以点表示出分布形态，根据分布形态来判断对应数据之间的相互关系。

其功能与鱼骨图类似，主要是了解原因与结果关系是否有相关，相关的程度如何。

也有人称之为"散点图"或"相关图"。

鱼骨图可以看作是定性查找原因的工具；散布图可以看作是定量查找原因的工具。

鱼骨图一般可以大致了解哪些要因会影响最后的结果，散布图也是以这种因果关系的方式来表示其关联性，并将因果关系所对应变化的数据分别点绘在X、Y轴坐标的象限上，以观察其中的相关性是否存在。

二散布图的用途（WHY）（一）能大概掌握原因与结果之间是否有相关及相关的程度如何。

例如患者满意度与候诊时间的关系。

（二）能检视离岛现象是否存在，以确定产生结果的关键因素。

（三）原因与结果相关性高时，两者可互为替代变量。

对于参数特性的掌握，可从原因或结果中对一个较易观测的变量予以监测，从而可根据所观察的变量的变化来推断另一个变量的变化情况。

三散布图的实施步骤（HOW）（一）确定要调查的两个变量，收集相关的数据，至少30组以上，并整理后写人数据表中。

数据太少时无法明确判断相互间的关系，所以至少应在30组以上。

（二）找出两个变量的最大值与最小值。

（三）画出纵轴与横轴刻度，计算组距。

收集的数据都是相对应数据，一般以横轴代表原因，纵轴代表结果。

特别要注意一点，横轴和纵轴的长度要差不多一样长，不可以相差太多，否则在图形上将无法判断它们的相关性。

组距的计算应以数据中的最大值减去最小值，原因与结果两个数据都必须计算出来，将组距除以轴长即得知每一个刻度的数值。