QC七大手法之散布图

QC7大手法及举例说明QC七大手法：层不法，柏拉图，特性要因图，散布图，查核表，直方图，管制图1 层不法层不法是所有手法中最差不多的概念，亦立即多种多样的资料，因应目的的需要分类成不同的[类不]，使之方便以后的分析。

一样工厂所做的层不通常为[空间不]，如作业员：不同班组不机器：不同机器不原料、零件：不同供给厂家作业条件：不同的温度、压力、湿度、作业场所….产品：不同产品不不同批不：不同时刻生产的产品将所要进行的项目利用统计表进行区不，这是运用统计方法作为治理的最基础工具。

在学校里某一学生考试成绩5科总分为440分，各（分类成绩如下：语文95分、英文92分、数学90分、历史85分，地理78。

加以分类后，可得之哪一科最高、哪一科最低，易于采取因应措施。

X X公司注塑机系三班轮班，前周三班所生产的产品均为同一产品，结果为班不A B C项目产量（件）10000 10500 9800以班不来加以统计，可得知各班的产量及不良率状况，以便于有依据地采取措施。

层不法的应用，要紧是一种系统概念，即在于要想把相当复杂的资料进行处理，就需明白得如何把这些资料加以有系统有目的加以分门不类的归纳及统计。

科学治理强调的是以治理的技法来补偿以往靠体会靠直觉判定的治理的不足。

而此治理技法，除了建立正确的理念外，更需要有数据的运用，才有方法进行工作解析及采取正确的措施。

如何建立原始的数据及将这些原始数据依所需要的目的进行集计，也是诸多品管手法的最基础工具。

再举个例子：国内航空市场近几年随着开放而竞争日趋猛烈，航空公司为了争取市场，除了加大各种措施外，也在服务品质方面下功夫。

我们也能够经常在航机上看到客户中意度的调查。

此调查是通过调查表来进行的。

调查表的设计通常分为地面的服务品质及航机上的服务品质。

地面又分为订票、候机；航机又分为空服态度、餐饮、卫生….等。

透过这些调查，将这些数据予以集计，就可得到从何处加大服务品质了。

2 柏拉图在工厂里，要解决的咨询题专门多，但往往不知从哪里着手，但事实上大部分的咨询题，只要能找出几个阻碍较大的要因，并加以处置及操纵；就可解决咨询题的80％以上，柏拉图是按照归集的数据，以不良缘故、不良状况发生的现象，有系统地加以项目不（层不）分类，运算出各项目不所产生的数据（如不良率、缺失金额）及所占的比例，再按照大小顺序排列，再加上累积值的图形。

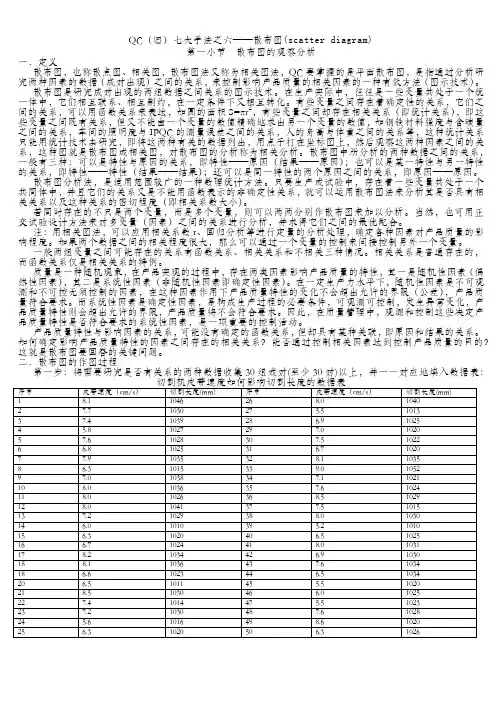
QC（旧）七大手法之六——散布图(scatter diagram)第一小节散布图的观察分析一．定义散布图，也称散点图、相关图，散布图法又称为相关图法，QC要掌握的是平面散布图，是指通过分析研究两种因素的数据（成对出现）之间的关系，来控制影响产品质量的相关因素的一种有效方法（图示技术）。

散布图是研究成对出现的两组数据之间关系的图示技术。

在生产实际中，往往是一些变量共处于一个统一体中，它们相互联系、相互制约，在一定条件下又相互转化。

有些变量之间存在着确定性的关系，它们之间的关系，可以用函数关系来表达，如圆的面积S=πr2，有些变量之间却存在相关关系（即统计关系），即这些变量之间既有关系，但又不能由一个变量的数值精确地求出另一个变量的数值，如钢铁材料强度与含碳量之间的关系，车间的照明度与IPQC的测量误差之间的关系，人的身高与体重之间的关系等，这种统计关系只能用统计技术去研究，即将这两种有关的数据列出，用点子打在坐标图上，然后观察这两种因素之间的关系，这种图就是散布图或相关图，对散布图的分析称为相关分析。

散布图中所分析的两种数据之间的关系，一般有三种：可以是特性与原因的关系，即特性——原因（结果——原因）；也可以是某一特性与另一特性的关系，即特性——特性（结果——结果）；还可以是同一特性的两个原因之间的关系，即原因——原因。

散布图分析法，是适用范围较广的一种数理统计方法。

只要生产或试验中，存在着一些变量共处于一个共同体中，并且它们的关系又是不能用函数表示的非确定性关系，就可以运用散布图法来分析其是否具有相关关系以及这种关系的密切程度（即相关系数大小）。

若同时存在的不只是两个变量，而是多个变量，则可以两两分别作散布图来加以分析。

当然，也可用正交试验设计方法来对多变量（因素）之间的关系进行分析，并求得它们之间的最优配合。

注：用相关图法，可以应用相关系数r、回归分析等进行定量的分析处理，确定各种因素对产品质量的影响程度。

第九章 散布图(Scatter Diagram)一、前言散布图有以下的作用：⒈能大概掌握缘故与结果之间是否有关联及关联的程度如何。

图2-1。

⒉能检查离岛现象是否存在。

图2-2。

⒊缘故与结果关联性高时，二者可互为替代变数。

关于过程参数或产品特性的掌握，可从缘故或结果中选择一较经济性的变数予以监测。

同时可通过观看一变数的变化来明白另一变数的变化。

二、散布图的定义特性要因图（鱼骨图）大概能够了解工程上那些缘故会阻碍第九章 散布图 145XX产品的质量特性，散布图也是以这种因果关系的方式来表示其关连性。

并将因果关系所对应变化的数据分不点绘在x—y轴坐标的象限上，以观看其中的关联性是否存在。

三、散布图的制作方法以横轴（X轴）表示缘故，纵轴（Y轴）表示结果，作法如下：⒈收集成对的数据(x1,y1)，(x2,y2)，…整理成数据表。

146 品管七大手法⒉找出x,y的最大值及最小值。

⒊以x,y的最大值及最小值建立x—y坐标，并决定适当刻度便于绘点。

⒋将数据依次点于x—y坐标中，两组数据重复时以☉表示，三组数据重复时以表示。

⒌必要时，可将相关资料注记在散布图上。

⒍散布图的注意事项： ⑴是否有异常点：有异常点时，不可任意删除该异常点，除非异常的缘故已确实掌握。

⑵是否需分层：数据的获得常常因为操作人员、方法、材料、设备或时刻等的不同，而使数据的关联性受到扭曲。

a. 全体时低度关联，分层后高度关联。

b. 全体时高度关联，分层后低度关联。

第九章 散布图 147YX Y XY Y Y⑶散布图是否与原有技术、经验相符：散布图若与原有技术、经验不相符时，应追查缘故与结果是否受到其他因素干涉。

四、散布图的判读依散布图的方向、形状，有以下几种关联情形：⒈完全正（负）关联：点散布在一直线上。

X X关X X⒉高度正(负)关联：缘故(X)与结果(Y)的变化近于等比例。

3.(X)4.(X)148 品管七大手法X XX X5.(Y)的变化完全不成比例。