立体图形、截面图形、投影图形的画法

初中数学如何绘制立体图形的投影绘制立体图形的投影需要一定的几何知识和绘图技巧。

下面将详细介绍绘制立体图形投影的步骤和方法。

1. 确定投影平面：首先，需要确定立体图形的投影平面。

投影平面可以是水平面、垂直面或其他平面。

根据需要，选择合适的投影平面。

2. 绘制基本形状：根据立体图形的形状，绘制基本形状的投影。

例如，如果立体图形是一个长方体，可以先绘制长方形的投影。

如果立体图形是一个球体，可以绘制一个圆的投影。

3. 定位顶点和边：根据立体图形的顶点和边的位置，使用几何知识将它们定位到投影平面上。

可以利用垂直投影或平行投影的方法。

-垂直投影：将立体图形的顶点和边垂直地投影到投影平面上。

使用垂直投影可以保持立体图形的形状和大小不变。

在投影平面上，使用垂直线表示立体图形的边。

-平行投影：将立体图形的顶点和边平行地投影到投影平面上。

使用平行投影可以保持立体图形的形状和大小不变。

在投影平面上，使用平行线表示立体图形的边。

4. 连接顶点和边：在投影平面上，根据立体图形的顶点和边的位置，连接顶点和边，绘制立体图形的投影。

-在平行投影中，使用平行线连接顶点和边。

-在垂直投影中，使用垂直线连接顶点和边。

5. 添加细节：根据需要，可以添加立体图形的细节，如曲线、阴影等。

这样可以使投影更加真实和逼真。

绘制立体图形的投影需要具备几何知识和绘图技巧。

对于不同类型的立体图形，可以选择不同的投影方法和投影平面。

在绘制过程中，要注意保持正确的比例和尺寸，以确保投影的准确性。

总结起来，绘制立体图形的投影需要以下步骤：确定投影平面、绘制基本形状、定位顶点和边、连接顶点和边，并添加细节。

通过正确选择投影方法和投影平面，可以准确地表示立体图形在二维投影平面上的形状和尺寸。

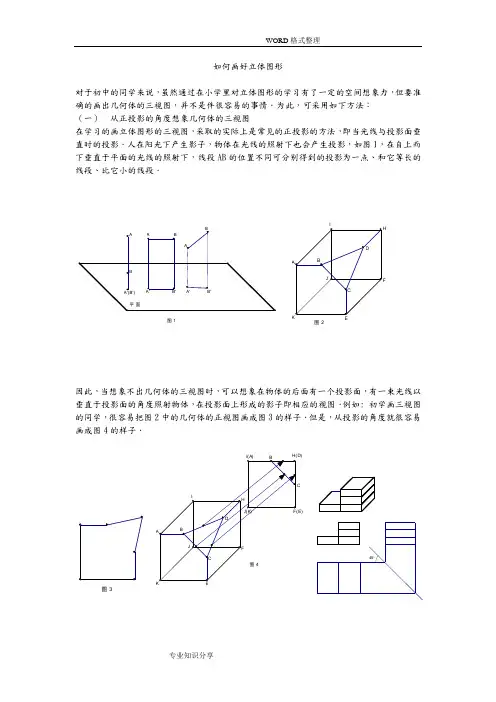
如何画好立体图形对于初中的同学来说，虽然通过在小学里对立体图形的学习有了一定的空间想象力，但要准确的画出几何体的三视图，并不是件很容易的事情．为此，可采用如下方法：（一） 从正投影的角度想象几何体的三视图在学习的画立体图形的三视图，采取的实际上是常见的正投影的方法，即当光线与投影面垂直时的投影．人在阳光下产生影子，物体在光线的照射下也会产生投影，如图1，在自上而下垂直于平面的光线的照射下，线段AB 的位置不同可分别得到的投影为一点、和它等长的线段、比它小的线段．因此，当想象不出几何体的三视图时，可以想象在物体的后面有一个投影面，有一束光线以垂直于投影面的角度照射物体，在投影面上形成的影子即相应的视图．例如: 初学画三视图的同学，很容易把图2中的几何体的正视图画成图3的样子．但是，从投影的角度就很容易画成图4的样子．图345图 1图 2（二）用45º线的方法形成对应因为三视图中的正视图和俯视图都反映几何体的长，所以在画三视图时，正视图和俯视图在长上应保持一致，同理，正视图和左视图应在高上保持一致，左视图和俯视图应在宽上保持一致．在这几种保持一致的对应上，左视图和俯视图的一致比较难掌握，而画45º线的方法则可以使它们之间保持很好的一致．具体画法为：1．确定主视图的位置，画出主视图；2．在主视图正下方画出俯视图，注意与主视图“长对正”；3．在主视图正右方画出左视图，注意与主视图“高平齐”，与俯视图“宽相等”；4．为表示出旋转几何体（圆柱、圆锥、球等）的对称轴，可在视图中加画点划线。

《几何画板》在数学教学中的应用对于数学科学来说主要是抽象思维和理论思维，这是事实；一个没有得到形象思维培养的人会有很高的抽象思维、理论思维的能力。

同样，一个学生如果根本不具备数学想象力，要把数学学好那也是不可能的。

因此，随着计算机多媒体的出现和飞速发展，在网络技术广泛应用于各个领域的同时，也给学校教育带来了一场深刻的变革──用计算机辅助教学，改善人们的认知环境──越来越受到重视。

立体图形怎么画立体图形是由三维空间中的几何体构成的，具有长度、宽度和高度三个方向。

常见的立体图形有立方体、长方体、球体、圆锥体、圆柱体等。

在绘制立体图形时，需要遵循一定的规律和技巧，以获得更加真实、精确和美观的效果。

下面将介绍如何绘制常见的立体图形，并提供相关的绘图技巧和实例。

1.立方体的绘制立方体是一种六面体，每个面都是一个正方形。

在绘制立方体时，需要先画定位线，然后绘制正方形的平面，再将他们合成一个六面体。

（1）先画出一个正方形，作为立方体的底面，在底面四个顶点处描绘四个边向上的垂直线，这些线应高出底面边的长度，相交处即为顶部的四个点。

（2）连接底面和顶部，从每个底面上端平行线向上连接，然后向下连接到相应的垂直线，再连接相邻的线段，即得到了一个完整的立方体。

绘制立方体时需要注意以下几点：（1）定位线和平面的尺寸应该相同，以确保立方体的比例正确。

（2）在制作六个正方形时，要保证它们的边缘互相平行，这有助于提高图形的准确性。

（3）在绘制各个面时，应遵循透视原理，即远离我们的面会缩小，而靠近我们的面会增大。

2.长方体的绘制长方体是一种六面体，由两个平行的长方形作为顶部和底部，以及四个矩形作为侧面组成。

与立方体类似，绘制长方体时也需要先绘制定位线和平面。

（1）确定长方体的长度、宽度和高度，以此在画面上虚构出一个长方体的框架。

（2）在底面四个顶点处描绘四个边向上的垂直线，这些线应高出底面边的长度，相交处即为顶部的四个点。

（3）连接底面和顶部，从每个底面上端平行线向上连接，然后向下连接到相应的垂直线，再连接相邻的线段，即得到了一个完整的长方体。

绘制长方体时需要注意以下几点：（1）与立方体相同，定位线和平面的尺寸应该相同，以确保长方体的比例正确。

（2）在制作顶部和底部的两个长方形时，要确保它们的边缘互相平行，这有助于提高图形的准确性。

（3）在绘制矩形时，应遵循透视原理，以确保各个侧面的比例正确。

3.球体的绘制球体是一种三维圆形体，由无数平行的圆形组成，可以绘制出不同的大小和形状。

初中数学如何绘制立体图形的投影绘制立体图形的投影是初中数学中的重要内容，它可以帮助我们更好地理解三维物体在二维平面上的表现。

在绘制立体图形的投影时，我们需要掌握一些基本的技巧和方法。

下面我将为你详细介绍如何绘制立体图形的投影。

一、绘制平面投影平面投影是指将一个三维物体的影像投影到一个平面上。

根据投影方向的不同，平面投影可以分为正射投影和斜投影。

在绘制平面投影时，我们可以通过以下步骤进行操作：1. 确定投影平面：首先，确定要将物体投影到的平面。

这个平面可以是水平的、垂直的或斜的，具体根据题目或需要来确定。

2. 确定投影方向：根据题目要求或需要，确定投影的方向。

例如，俯视图、正视图、侧视图等。

3. 绘制主要轮廓线：根据物体的主要轮廓线，在投影平面上绘制出物体的主要形状。

4. 绘制次要轮廓线：根据物体的次要轮廓线，在投影平面上绘制出物体的次要形状。

5. 补充细节：根据需要，可以在投影图中添加一些细节，如标记点、标尺、坐标轴等。

二、绘制正交投影正交投影是指将三维物体的各个面分别投影到与其平行的投影面上。

在绘制正交投影时，我们可以通过以下步骤进行操作：1. 确定投影平面：首先，确定要将物体投影到的平面。

这个平面可以是水平的、垂直的或斜的，具体根据题目或需要来确定。

2. 确定投影方向：根据题目要求或需要，确定投影的方向。

例如，主视图、副视图等。

3. 绘制主视图：根据物体的主要轮廓线，在投影平面上绘制出物体的主视图。

主视图通常选择与物体的主轴平行的投影面。

4. 绘制副视图：根据物体的次要轮廓线，在投影平面上绘制出物体的副视图。

副视图通常选择与物体的副轴平行的投影面。

5. 补充细节：根据需要，可以在投影图中添加一些细节，如标记点、标尺、坐标轴等。

三、绘制斜投影斜投影是指将三维物体的各个面分别投影到一个与其不平行的投影面上。

在绘制斜投影时，我们可以通过以下步骤进行操作：1. 确定投影平面：首先，确定要将物体投影到的平面。

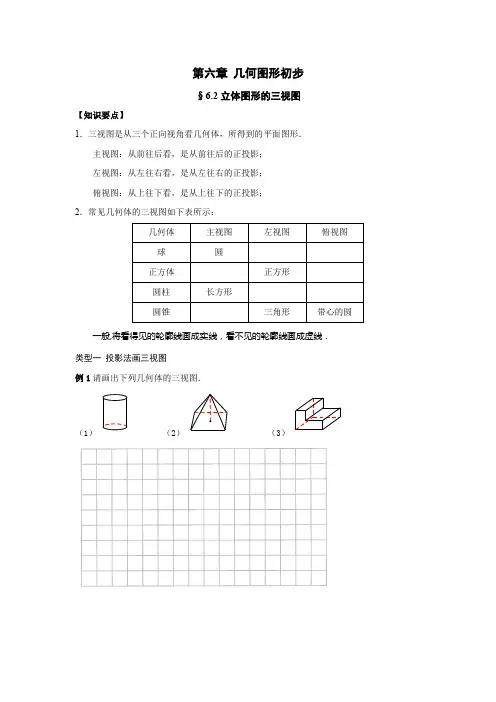
第六章几何图形初步
§6.2立体图形的三视图
【知识要点】
1．三视图是从三个正向视角看几何体，所得到的平面图形．主视图：从前往后看，是从前往后的正投影；
左视图：从左往右看，是从左往右的正投影；
俯视图：从上往下看，是从上往下的正投影；
2．常见几何体的三视图如下表所示：
一般,将看得见的轮廓线画成实线，看不见的轮廓线画成虚线．类型一投影法画三视图
例1请画出下列几何体的三视图．
（1）（2）（3）
练习1请画出下列几何体的三视图．
（1）（2）（3）（4）
类型二从不同方向看立体图形
例2如图是由5个相同的小正方体搭成的几何体，从上面看到的形状图是( )
A．B．C．D．
练习2请画出下列几何体的三视图．
（1）（2）
（3） （4）
类型三 根据不同方向看到的图形还原几何体的形状
例3如图用若干小正方体搭成的几何体的三视图，则原几何体是( )
A ．
B ．
C ．
D ．
练习3（1）如图是几个小正方体搭成的几何体的三视图，则原几何体中小正方体的个数为 ；
（2）若正方体的棱长为1，则还原后的几何体的表面积为对少？
主视图
左视图
俯视图
俯视图
左视图
主视图
练习4如图是几个小正方体搭成的几何体的俯视图，其中数字表示从上面看一列有几个小正方体，请画出主视图和左视图．
2
21
1
主视图
左视图。

立体图形怎么画引言立体图形是由三维空间中的点、线、面组成的图形。

在绘画和设计中，了解如何画立体图形是非常重要的。

本文将介绍一些常见的立体图形，并提供简单易懂的步骤来帮助你画出精确的立体图形。

1. 立体图形的基本概念在开始画立体图形之前，我们先来了解一些基本概念。

1.1 点、线、面•点：在三维空间中，点是没有长度、宽度和高度的。

它是空间中一个确定的位置。

•线：点可以通过连线来形成线。

线由无数个点组成，它们相互连接，有一定的长度和方向。

•面：三个或更多线可以形成一个面。

面有长度和宽度，但没有高度。

1.2 立体图形的分类常见的立体图形可以分为以下几种：•球体：具有圆心和半径，表面是由无数个相同的曲线组成的。

•长方体：具有六个面，每个面都是一个矩形。

•正方体：是一种特殊的长方体，具有六个面，每个面都是正方形。

•圆锥体：由一个圆形底面和一个顶点连接而成，侧面是由无数个扇形组成的。

2. 画立体图形的步骤现在，让我们分别介绍如何画球体、长方体、正方体和圆锥体。

以下是每种立体图形的具体步骤。

2.1 画球体画球体可以通过以下步骤进行：1.画一个圆，它将成为球体的截面。

2.从圆的中心点开始，在圆上划出一条半径。

3.依次从圆的边缘上的每个点划出一条相同长度的线，使这些线都通过圆心。

4.这些线将形成一系列扇形，用曲线将它们连接起来。

5.将扇形连接起来，形成球体的外表。

2.2 画长方体画长方体可以通过以下步骤进行：1.画一个矩形，它将成为长方体的一个面。

2.在矩形的一边上选择一个点，画一条与矩形边平行的线段，这将成为长方体的高度。

3.从矩形的另一个边上的相应位置开始，画一条与高度线平行的线段，它将成为长方体的另一条边。

4.从矩形的对角线上的相应位置开始，画一条与高度线平行的线段，它将成为长方体的第三条边。

5.这样，你就画出了长方体的外表。

2.3 画正方体画正方体可以通过以下步骤进行：1.画一个正方形，它将成为正方体的一个面。

分析立体图形的投影和截面立体图形是指具有长度、宽度和高度的图形，它们在三维空间中存在着。

在现实生活中，我们常常会遇到各种不同形状的立体图形，如长方体、圆柱体、球体等。

对于这些立体图形，我们可以通过投影和截面的方法进行分析。

一、投影投影是指将三维立体图形映射到二维平面上，以便更好地观察和分析其形状、结构等特征。

常见的投影方式有平行投影和透视投影两种。

1. 平行投影平行投影是指将立体图形的每个顶点在平行于某一方向的平面上投影，得到的是一个与原图形相似但比例不同的平面图形。

例如，沿着水平方向进行平行投影，我们可以得到一个俯视图，展示出立体图形在水平方向上的特征。

2. 透视投影透视投影是指以某一视点为中心，将图形的各个点以透视关系投影到一个平面上。

透视投影更接近于人眼观察物体的方式，能够更真实地呈现出立体图形的空间感。

例如，我们常见的透视图就是使用透视投影得到的。

二、截面截面是指将立体图形与一个平面相交后，所得到的图形形状。

通过对不同位置和角度的截面进行观察和分析，我们可以了解立体图形在不同方向上的特征。

1. 平行截面平行截面是指将平行于某一方向的平面与立体图形相交，所得到的截面图形。

通过平行截面，我们可以观察到图形在该方向上的特征，例如一个圆柱体的平行截面是一个圆。

2. 垂直截面垂直截面是指将垂直于某一方向的平面与立体图形相交，所得到的截面图形。

通过垂直截面，我们可以观察到图形在该方向上的特征，例如一个长方体的垂直截面是一个矩形。

通过投影和截面的方法，我们可以更好地理解和分析立体图形。

它们帮助我们揭示立体图形的特征和结构，以及在工程、建筑、设计等领域的应用。

总之，立体图形的投影和截面是我们研究和了解立体图形的重要工具，可以帮助我们更好地认识和应用立体图形。

通过以上的分析我们可以看出，投影是将三维图形映射到二维平面上，分析其形状和结构；而截面则是通过将图形与平面相交，观察和分析图形在不同方向上的特征。

这两种方法都有助于我们更好地理解和应用立体图形，对于计算机图形学、工程建模等领域也有重要意义。

截面画法大全高中数学
在高中数学中，截面画法通常用于解决立体几何问题，特别是涉及到计算空间中的距离、角度等问题。

以下是一些基本的截面画法：
1. 水平截面法：这是最常见的截面画法，即在平面中通过一个水平切割来观察立体图形。

例如，如果你想要计算一个圆柱体的高度，你可以通过在底部垂直切割来得到一个水平截面，然后通过测量截面中圆形周长的一半（即圆柱体的底面直径），再根据圆周长公式计算出高度。

2. 垂直截面法：这与水平截面法类似，只是在平面中通过一个垂直切割来观察立体图形。

例如，如果你想要计算一个圆柱体的底面半径，你可以通过在顶部水平切割来得到一个垂直截面，然后通过测量截面中圆形周长的一半，再根据圆周长公式计算出底面半径。

3. 正交截面法：这是在平面中通过一个既不是水平也不是垂直的切割来观察立体图形。

例如，如果你想要计算一个圆柱体的侧面积，你可以通过
在侧面倾斜切割来得到一个正交截面，然后通过测量截面中矩形的面积（即圆柱体的侧面积）。

以上就是高中数学中常见的截面画法，希望对你有所帮助。