匀变速圆周运动切向加速度和法向加速度

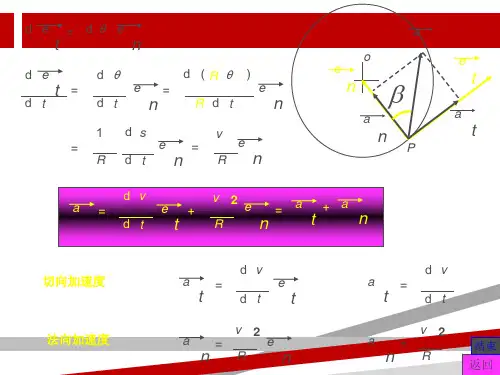
大学物理切向法向加速度.ppt

解：
ω dq
=
=c
2bt
dt
dw
=
= 2b
dt
a = R
=
t
2 bR
w a = R n
2 = R (c
2 b t )2
结束返回
圆周运动及其描述
一、切向加速度和法向加速度
a
a
=
dv e+
dt t
v 2e =
Rn
a+
t
a
n
o e
n
e
t
a
a
n
t
P
切向加速度
dv
a=
e
t
dt t
dv
a=
t
dt
法向加速度
1．李鸿章1872年在上海创办轮船招商局，“前10年盈和，成
为长江上重要商局，招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办
()
A．打破了外商对中国航运业的垄断
B．阻止了外国对中国的经济侵略
C．标志着中国近代化的起步
D．使李鸿章转变为民族资本家
解析：李鸿章是地主阶级的代表，并未转化为民族资本家；洋务运动标志着中国近代化的开端，但不是具体以某个企业的创办为标志；洋务运动中民用企业的创办在一定程度上抵制了列强的经济侵略，但是并未能阻止其侵略。故B、C、D 三项表述都有错误。答案：A
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应
时代潮流
图说历史
主旨句归纳
(1)近代交通由传统的人力工具逐渐演变为
机械动力牵引的新式交通工具，火车、
汽车、电车、轮船、飞机先后出现。
(2)通讯工具由传统的邮政通信发展为先进

大学物理切向加速度和法向加速度

科研探索
在物理学、天文学、生物学等科研领域，切向加速度和法向加速度的应用对于探索物体运动规律和现象具有重要作用，能够促进科学研究的深入开展和创新。
THANKS FOR WATCHING
感谢您的观看
曲线运动中的切向加速度
在曲线运动中，切向加速度等于物体速率对时间的变化率，即$a_{t} = frac{dv}{dt}$。
3
匀速圆周运动中的切向加速度
在匀速圆周运动中，切向加速度的大小为$a_{t} = omega^{2}r$，方向始终指向圆心。
切向加速度在现实生活中的应用
车辆转弯
汽车在转弯时，由于离心力作用，车轮与地面之间产生侧向摩擦力，
工程设计和优化
在机械、航空、交通等领域，切向加速度和法向加速度的应用对于工程设计和优化至关重要，能够帮助工程师更好地分析物体的运动特性和受力情况，提高设计质量和安全性。
体育科技
在体育领域，切向加速度和法向加速度的应用对于运动分析和技术优化具有重要意义，能够帮助教练和运动员更好地理解运动过程中的技术细节和改进方向。
使汽车产生切向加速度，影响车辆行驶稳定性。
旋转机械
旋转机械在运转过程中，由于摩擦力或外部扰动作用，会产生切向加速度，影响机械的正常运转。
投掷运动
在投掷运动中，如标枪、铁饼等，运动员通过施加切向力使器械产生切向加速度，从而影响器械飞行的轨迹和距离。
03 法向加速度
法向加速度的概念
法向加速度是描述物体在圆周运动或曲线运动中速度方向变化快慢的物理量。
在不同运动状态下的表现
01
02
03
匀速圆周运动
切向加速度为零，法向加速度不为零，物体做匀速圆周运动。

自然坐标系

r

t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a

an

v2 R

vB

B vA
R

O
A
大小，方向，作用
2. 一般圆周运动的
切向加速度和法向加速度分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er

ds dt
er

ds dt
三、自然坐标系下的加速度
1. 匀速圆周运动，法向加速度
v vB
vA

v vB
vA
Δv vB vA ,

AB R
lim lim ar
t 0
则：a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略：
（1）分析问题特点，建立恰当的坐标系（2）由运动方程求解速度随时间变化的表达式（3）分别计算出切向加速度与法向加速度，再求解合加速度的大小和方向
解：根据加速度的定义：
ar
anern
a er

v2 R
ern

dv dt
er
a an2 a 2
v

ds dt
2
R
a

d
dt
1.2t

切向加速度和法向加速度的数学表达式及其意义

切向加速度和法向加速度的数学表达式及其意义在物理学中，我们经常会遇到物体在运动中所受到的加速度。

加速度可以分为两个方向，即切向加速度和法向加速度。

本文将介绍并解释切向加速度和法向加速度的数学表达式，以及它们在物理学中的意义。

一、切向加速度的数学表达式与意义切向加速度是物体在运动轨迹上的变化速率，也可以理解为物体在运动过程中速度的变化率。

它的数学表达式可以用以下公式表示：at = dv/dt其中，at表示切向加速度，v表示物体的速度，t表示时间。

这个公式表明切向加速度等于速度对时间的导数。

切向加速度的意义在于描述了物体在轨迹上改变方向所产生的加速度。

当物体沿着曲线运动时，速度方向在不断改变，因此切向加速度将用于量化速度方向的变化。

切向加速度的大小取决于速度的变化率和物体的质量。

如果物体的速度越快，切向加速度也会相应增大。

二、法向加速度的数学表达式与意义法向加速度是物体在曲线上运动时的向心加速度，也称为离心加速度。

它表明物体在曲线上偏离直线运动时所受到的向心力和加速度。

法向加速度的数学表达式可以用以下公式表示：an = v²/r其中，an表示法向加速度，v表示物体的速度，r表示曲线的半径。

法向加速度的意义在于描述了物体在曲线上半径方向的加速度。

当物体沿着曲线运动时，它将受到向心力的作用，使它偏离直线运动。

法向加速度的大小取决于物体的速度和曲线的半径。

如果物体的速度越快或曲线的半径越小，法向加速度也会相应增大。

三、切向加速度和法向加速度的关系与实例分析切向加速度和法向加速度是相关联的。

在物体沿着曲线运动时，它们的关系可以通过以下公式表示：a = √(at² + an²)其中，a表示总加速度，at表示切向加速度，an表示法向加速度。

这个公式表明了切向加速度和法向加速度的平方和等于总加速度的平方。

它们在矢量运算中也有着重要的作用。

举例来说，当一个车辆在一个转弯处加速时，它会受到切向加速度和法向加速度的影响。

大学物理3切向法向加速度

01
车辆行驶过程中的转弯
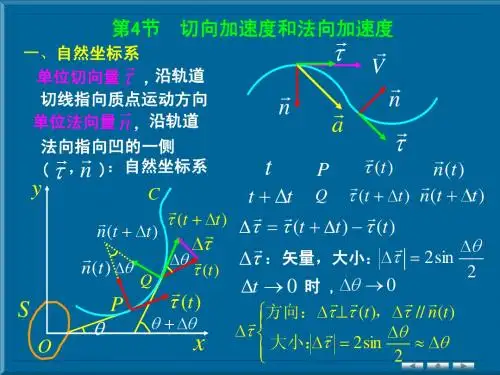
在转弯过程中，车辆的切向加速度和法向加速度共同作用，使车辆按照
预定的轨迹行驶。
02
投掷物体的运动
在投掷物体时，出手的瞬间切向加速度和法向加速度达到最大值，共同
决定了物体的飞行轨迹。
03
天体运动
在天体运动中，行星绕太阳运动的轨迹是一个椭圆，切向加速度和法向
加速度的大小和方向不断变化，共同决定了行星的运动状态。
03
当物体沿着抛物线轨道运动时，法向加速度的计算公式为： an = v^2 / p，其中p表示抛物线的焦距。
法向加速度的物理意义
法向加速度的物理意义在于描述物体运动方向改变的快慢程度。
法向加速度越大，表示物体运动方向的改变越快，物体运动的曲
率越大。
在圆周运动中，法向加速度的大小决定了物体运动的角速度和周期，其值越大则角速度和周期越
在车辆设计过程中，需要考虑轮胎与地面的摩擦力、悬挂系统的设计以及轮胎的弹性等因素，以确保车辆在行驶过程中的稳定性和安全性。
飞行器飞行中的切向法向加速度
飞行器飞行中的切向法向加速度
在飞行器飞行过程中，由于气流的压力和摩擦力作用，会产生切向加速度，使飞行器产生偏航或滚转动作。同时，由于飞行器的翼型设计和气动布局，会产生法向加速度，使飞行器在飞行过程中保持稳定。
小。
03
CATALOGUE
切向法向加速度的关系
切向法向加速度的关联性
切向法向加速度是描述物体运动状态的两个重要参数，它们
之间存在一定的关联性。
当物体做曲线运动时，切向加速度决定物体运动轨迹的弯曲程度，法向加速度则与物体偏离轨迹的方向有关。
切向加速度和法向加速度的大小和方向共同决定了物体的运

1-3切向加速度法向加速度

第1.3.2节切向加速度法向加速度
一、自然坐标系 •问题的提出：在直角坐标系中，加速度公式无法看出哪一部分是由速度大小变化产生的加速度，哪一部分是由速度方向变化产生的加速度，所以引入自然坐标系来描写。 1.自然坐标系自然坐标系是建立在物体运动的轨迹上的，有两个坐标轴，切向坐标和法向坐标。
速率对时间求一阶导数
v an r
2
r 为运动轨迹的曲率半径。
例：一质点作半径为R的圆周运动，其速率满足 v kRt ， k为常数，求：切向加速度、法向加速度和加速度的大小。
dv at kR 解：切向加速度 dt 2 2 v ( kRt) 2 2 法向加速度 an k Rt r R 2 2 加速度 a a an

kR k Rt
2 2
2 2
讨论下列几种运动情况（物体分别做什么运动）：
1. at 0 , an 0 匀速直线运动；
2. at C , an 0
3. at 0 , an C 4. at 0 , an 0
匀变速直线运动；
匀速率圆周运动；变速曲线运动；
•切向坐标 t沿运动轨迹的切线方向； •法向坐标 n 沿运动轨迹的法线方向。
n
n
二、切向加速度、法 v an = dt R
2
切向加速度
法向加速度
at an
由于速度大小变化产生的加速度；由于速度方向变化产生的加速度。
可以证明：
dv at dt

切向加速度和法向加速度课件

在圆周运动中，法向加速度的大小与半径和线速度的平方成正比。
法向加速度的计算公式
在圆周运动中，法向加速度的大小可以通过公式an = v²/r计算，其中an表示法向加速度，v表示线速度，r表示半径。
对于一般的曲线运动，法向加速度的大小可以通过公式an = dv/dt计算，其中an 表示法向加速度，dv/dt表示速度的变化率。
03 切向加速度与法向加速度的关系
圆周运动中的切向加速度与法向加速度
切向加速度
描述物体在圆周运动中速度大小的变化，即线速度的变化率。
法向加速度
描述物体在圆周运动中速度方向的改变，即角速度的变化率。
曲线运动中的切向加速度与法向加速度
切向加速度
描述物体在曲线运动中速度大小的变化。
法向加速度
描述物体在曲线运动中速度方向的改变。
在航天器进行轨道变化时，需要产生法向加速度来改变其轨道半径或轨道倾角。这可以通过调整发动机推力和飞行姿态来实现。
切向加速度与法向加速度在日常生活中的应用
游乐设施
游乐场中的过山车、旋转木马等设施利用了切向加速度和法向加速度的原理，使游客能够体验刺激和乐趣。
体育竞技
在赛车、自行车等竞技项目中，运动员通过控制切向加速度和法向加速度来提高速度、改变运动方向或完成特定动作。
切向加速度和法向加速度课件
• 切向加速度与法向加速度的关
目
录
• 切向加速度和法向加速度的应
• 切向加速度和法向加速度的实
01 切向加速度
切向加速度的定义
切向加速度
描述物体在圆周运动或曲线运动中，沿运动轨迹切线方向的加速度。
公式表示
at = d^2r/dt^2 ，其中 r 为物体在曲线上的位置矢量，t为时间。

切向加速度和法向加速度

r τ (t)
τ
r
θ
θ + θ
x
r τ r θ ：大小 τ = 2sin 2 ≈ θ
dτ dτ dθ dτ dθ ds dτ r ds = ρ ds =V = = , =n , dθ , dt dt dθ dt dθ ds dt dθ
r τ ≈ θ n r r r dτ r τ θ n r lim θ →0, θlim θ = θ →0 θ = n dθ = n →0
α
r a
an
dV 2 V 2 2 2 a = at2 + an = ( ) + ( ) , tgα = an / at dt ρ
讨论：（1 直线运动，讨论：（1）直线运动，ρ = ∞, an = 0 ：（ dV V2 a = 0, an = 匀速率圆周运动，（2）匀速率圆周运动， t = ：向心加速度 R dt 一般曲线运动及变速率圆周运动，（3）一般曲线运动及变速率圆周运动，at ≠ 0, an ≠ 0 V2 V2 （4） an = ρ= ：计算曲率半径
θ = 63.4o
第6节节
圆周运动的角量表示
角坐标， s = Rθ θ ：角坐标，rad θ = θ (t) s = s(t)
y
r P r s θ A R O
V = ωR,
dω d 2θ ：角加速度，角加速度， rad / s2 β= = 2 dt dt V 2 ω2 R2 = = ω2 R at = Rβ, an = R R
第5 节
相对运动
P
r r
S
O
静系
r r0
S′
O′
动系
r r′
r r r r = r ′ + r0 r r r dr dr ′ dr0 = + dt d = r′ + r0

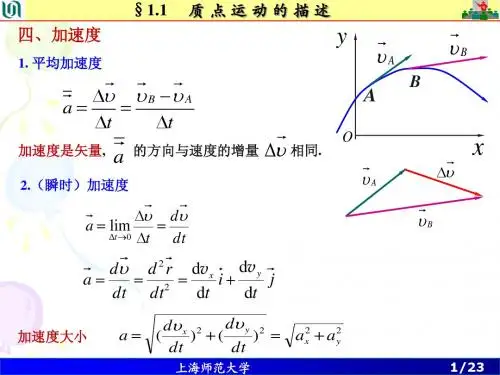
第 01章 2 次课 -- 加速度圆周运动

(4)
7 /23
§1.2
圆周运动
(4)
v(t) r(t)
(4)式就是质点作圆周运动时的速率与角速度的关系. 质点作圆周运动时, 速度方向不断改变, 因此圆周运动是变速运动 ! 有加速度 ! 圆周运动的加速度有什么特点 ?
o
v2 et 2 v1 et1
r
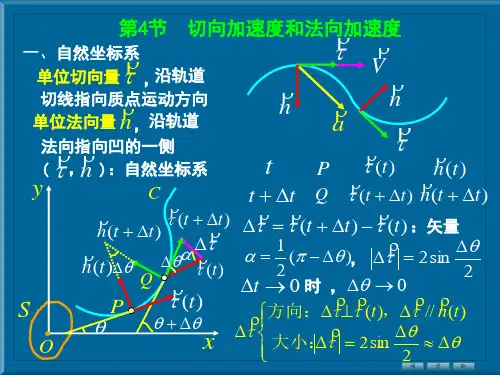
三、圆周运动的切向加速度和法向加速度
at r
也是常数
法向加速度
加速度
an r 2
2
r
不是常数 (10)
a at an r et r 2 en
d dt
设t=0时, =0, =0; 则

d dt
d dt
0 t
2 2 02 2 ( 0 )
即
dy 由速度的定义得 v v0 e 1.0t dt
两边积分, 得
dy 0e1.0t dt

y
0
dy v0 e-1.0t dt
0
t
即
y v0[1 e
]
y
代入初速度, 得
y 10[1 e1.0t ]
上海师范大学
2 /23
§1.1
质点运动的描述
v v0e
为小球已停止运动; （2）此球体在停止运动前经历的路程有多长？
解：如图建立坐标系.
由加速度定义得
v
a
t dv 两边积分, 得 1.0 dt v0 v 0
d 1.0 dt
即
d 1.0dt
1.0t
o
v0
-1.0t
即
lnv - ln0 1.0t
化简得

03运动学圆周运动 (自然坐标系、角速度、角加速度、切向加速度、法向加速度)

2
平均角加速度 t
t 0
瞬时角加速度 lim d
t dt
(SI)单位：rad/s2 角速度与角加速度都是矢量，角速度的方向由右手定则确定。（规定用右手螺旋定则来判定：四指方向为绕向，大拇指方向为角速度方向！！） α与ω同向。质点作加速圆周运动。
α与ω方向相反。质点作减速圆周运动。
Y
r
r =R
θ确定后：x=Rcosθ y=Rsinθ θ 单位 rad 弧度

t

θ=θ(t)
X
定义：角位置
角位移△θ=θ（t+ △t) -θ(t) 平均角速度瞬时角速度 (SI)单位：rad/s 弧度/秒工程单位 rev/min(转/分）
d lim t 0 t dt
9
4 平面运动的极坐标表示：
r
0
e

p
er
在平面内取一个定点O，叫极点，引一条射线Ox，叫做极轴，再选定一个长度单位和角度的正方向（通常取逆时针方向）。对于平面内任何一点M，用r表示线段OM的长度，θ表示从Ox到OM的角度，r叫做点M的极径，θ叫做点M的极角，有序数对 (r,θ)就叫点M的极坐标，这样建立的坐标系叫做极坐标系。
解法：用积分或求解微分方程的方法求解。
x x0 vdt
t0
t
v v0 adt
t0
t
12
an=gcos γ =gV x/V=9.13m/s2
aτ=gcosβ=gVy/V=3.53m/s2
ρ=V2/an=25.03m
11
5 质点运动学小结： 1、描述运动的物理量：t、Δt、r、Δr、v、a 、 s dv dr 加速度： a 2、定义：速度 v dt dt 对一维的情况：v=dx/dt a=dv/dt 3、质点运动学的两类问题： 1）已知运动方程，求速度、加速度。解法：用求导数的方法解决。 2）已知速度（或加速度）及初始条件求运动方程。

切向加速度和法向加速度

dV d 2s 切向加速度， at = = 2 ：切向加速度，速率变化引起的 dt dt r r方向， V V ↑, at > 0, 沿 τ 方向， ↓, at < 0,与 τ 反方向
an = V2
ρ
法向加速度， >0：法向加速度，速度方向变化引起的沿法线指向曲率中心
at
α
r dV 2 V2 2 2 a a = at2 +an = ( ) +( ) , tgα = an / at
r r r dV dV′ dV0 = + dt dt dt
r r r aB对A = aB −aA
例：汽车以20 汽车以20
m/ s
速度向东行驶，速度向东行驶，
雨滴在空气中以10 雨滴在空气中以10 m/ s 速度下落，求雨滴相对于汽车的速度解：地面： , 汽车： ′系地面：汽车： S S 车对地面的速度为牵连速度大小
消去时间变量可得轨迹方程：消去时间变量可得轨迹方程：
r e ：沿矢经方向 1 r r e2：垂直于 e 指向 θ ↑的方向 1
r = r(θ)
r r r 二、径向速度与横向速度 V =Vr e1 +V e2 θ r r r de1 dθ r
r V
V θ
dr dθ Vr = ：径向速度， V = r ：横向速度 θ dt dt y r 例：质点位于 P(x, y), 速度大小为 V r dr dr A， B， dt dt r P(x, y) r r dr D， (dx)2 + (dy)2 C， x O dt dt dt
θ =θ0 +ω t
匀变速圆周运动
x = x0 +Vt
匀加速直线运动

匀变速圆周运动切向加速度和法向加速度

匀变速圆周运动切向加速度和法向加速度匀变速圆周运动是物理学中经常讨论的一种运动状态，它的加速度分为两个方向，即切向加速度和法向加速度。

切向加速度是指物体在圆周运动中速度的大小不断变化，导致其方向发生改变所产生的加速度；而法向加速度则是指物体受到向心力的作用导致其沿着圆周方向运动时的加速度。

匀变速圆周运动的切向加速度可以通过求导速度大小得出，即
a_t=dv/dt。

而法向加速度则可以通过向心力公式F_c=m*v^2/R计算得出，其中m为物体质量，v为物体在圆周运动中的速度，R为圆周半径。

在匀变速圆周运动中，切向加速度和法向加速度可以相互影响，导致物体在圆周运动中的轨迹发生变化。

如果切向加速度和法向加速度大小相等，物体将沿着圆周方向做匀速直线运动；如果切向加速度大于法向加速度，物体将沿着圆周向外运动；反之，如果法向加速度大于切向加速度，物体将沿着圆周向内运动。

因此，在研究匀变速圆周运动时，切向加速度和法向加速度是非常重要的物理量，它们可以帮助我们理解物体在圆周运动中的行为和运动规律。

- 1 -。

大学物理12圆周运动

S系 (Oxyz)
基本参考系
S'系(O' x' y' z')
运动参考系
u是S’系相对S系
运动的速度
1-3 相对运动
yy'
P P'
*
oo'
xx'
t0
y
o
P
y'
D
r
P'
uQ
r'
xx'
ut o' t t
第一章质点运动学
22
物理学
第五版
位移关系
r r'D 或 r r'ut
速度变换
r r' u t t v v'u
理解伽利略速度变换式, 并会用它求简单的质点相对运动问题．
第一章质点运动学
2
物理学
第五版
质点运动的自然坐标描述
自然坐标系 —— 坐标原点固接于质点, 坐标轴沿质点运动轨道
1-2 圆周ev运t 动 evt B
的切向和法向的坐标系，叫做自
然坐标系。切向以质点前进方向 A
为侧正方，向记为做正，ev记t ，做法ev向n以。曲线凹
y
A
r
二圆周运动的角速度
❖ 角坐标 (t)
o
❖角位移
y
xx
B
❖ 角速度
lim
d
t0 t dt
r A
o
x
单位：rad·s-1
第一章质点运动学
4
物理学
第五版
1-2 圆周运动
❖ 速率 v lim Δs r lim Δθ
Δt0 Δt
Δt0 Δt

大学物理切向加速度和法向加速度

在实际问题中的应用选择
车辆行驶
在车辆行驶过程中，由于摩擦力和空气阻力的作用，车辆会受到切向加速度的影响，导致速度的变化；而转弯时，车辆还会受到法向加速度的作用，改变运动方向。Байду номын сангаас
航天器轨道
航天器在绕地球运行时，受到地球引力的作用产生法向加速度，使得航天器沿着预定轨道运行；同时，航天器在切线方向上也会受到其他力的作用，如太阳辐射压和大气阻力等，这些力产生的切向加速度会影响航天器的速度和轨道半径。
实验步骤与操作
准备实验器材
滑轮、细绳、重物、测量尺、计时器等。
VS
搭建实验装置
将滑轮固定在实验台上，细绳一端系住重物，另一端跨过滑轮并可调节长度。
实验步骤与操作
实验操作 1. 调整细绳长度，使重物做近似圆周运动。
2. 记录重物运动的速度和时间，通过测量尺测量轨道半径。
实验步骤与操作
3. 改变重物运动的速度，重复实验。
思考三
如何理解切向加速度和法向加速度在描述物体运动状态中的作用？
THANKS
感谢观看
详细描述
在卫星轨道计算中，需要根据切向加速度来计算卫星的速度和轨道半径；在曲线运动分析中，切向加速度用于描述物体在曲线运动中的速度变化。
02
法向加速度
定义与公式
定义
法向加速度是描述速度矢量方向改变的快慢程度的加速度，通常表示为an。
公式
an=v^2/r，其中v是速度大小，r是运动物体到圆心的距离。
在不同运动形式下的表现
匀速圆周运动
自由落体运动
在匀速圆周运动中，切向加速度为零，法向加速度等于向心加速度，方向始终指向圆心。
自由落体运动中，物体只受到重力的作用，切向加速度为零，法向加速度等于重力加速度，方向始终竖直向下。

圆周运动的角量描述角量与线量的关系

A
反映反映的方向变化因素
的大小变化因素
无限趋近法向
无限趋近切向
法向加速度
切向加速度
要点归纳法向加速度Fra bibliotek切向加速度
线量描述
切向加速度
0, , v 增大 at dv 0, , v 常量 dt 0, , v 减小
一般曲线运动（自然坐标）
y
a
o a x a
et
en
第三节
圆周运动
线量描述
1、自然坐标系：
切向：质点前进的方向法向：与切向垂直，指向曲线凹的一面。
et
en
2、圆周运动的切向加速度和法向加速度（自然
坐标系分析） S =S (t )
v v(t ),a a (t ) ds v et vet dt
线量描述
加速度问题
C
D B
截取 AD = AB 作矢量和
v et
v ds et vet dt 2 d v d v v a et en dt dt
ds 其中 d 为曲率半径 .
en
例
角位置
角位移
角速度
角加速度
匀变速圆周运动
角线量关系
物理量小结
物理量小结2
角线简例

大学物理第四章-刚体的转动-习题及答案

第 4 章刚体的定轴转动习题及答案
1．刚体绕一定轴作匀变速转动，刚体上任一点是否有切向加速度？是否有法向加速度？切向和法向加速度的大小是否随时间变化？
答：当刚体作匀变速转动时,角加速度不变。刚体上任一点都作匀变速圆周运动，因此该点速
率在均匀变化，v l ，所以一定有切向加速度 at l ，其大小不变。又因该点速度的方向变化，
ω dr
（1）圆盘上半径为r、宽度为dr的同心圆环所受的摩擦力矩
为
dM
m
(
R2
2 rdr)grBiblioteka 2r 2 mgdr/
R2
负号表示摩擦力矩为阻力矩。对上式沿径向积分得圆盘所受
r dF
的总摩擦力矩大小为
M dM R 2r2mgdrdr 2 mgR
0
R2
3
（2）由于摩擦力矩是一恒力矩，圆盘的转动惯量 I 1 mr2 ，由角动量定理可得圆盘停止的 2
度．
解：碰撞过程满足角动量守恒：
2 3
mv0l
1 2
mv0
2 3
l
I
而
I m( 2 l)2 2m(1 l)2 2 ml2
3
33
所以
mv0l
2 3
ml 2
由此得到： 3v0 2l
2m
1 3
l
O⅓l
1 2
v
0
2 3
l
m
⅓l m v0
⅓l
15. 如图所示，A和B两飞轮的轴杆在同一中心线上，设两轮的转动惯量分别为 JA＝10 kg·m2 和 JB
2
2
22
2
2
1 16
( Ld14
1 2
ad24

《大学物理》圆周运动

得切向加速度与角加速度的关系为a r
dt
而法向加速度an
v2 r
dt r 2
质点作匀变速圆周运动时的角速度、角位移与角加速度的关系式
为：
ω ω0 t
θ θ0 ω0t t 2 / 2
ω2 ω02 2 (θ θ0 )
v v0 at
x
x0
v0t
at2 / 2
v2
v02
2a( x
(R
sin
ti
R
c
ostj )
a(t)
dv(dtt)
2 (R
costi
R 2
sin tj)
dt
速度、加速度也可以用其在x、y方向上的分量来表示
二、自然坐标系下的描述
自然坐标系：以动点为坐标原点，以动点所在轨道处的切线和法线为坐标轴（切向指向前进方向，法向指向曲率中心），、n 为切、法向的单位矢量。
1-16.飞轮作匀减速转动 , 在 5 秒内角速度由 40πrad/s 减到 10πrad/s , 则飞轮在这 5秒内总共转过了多少圈?飞轮再经过多少时间才能停止转动?
课后习题 1-8 1-9 1-10
（2）如
匀变速直线运动
（3）如 a 0,a；则0 质点作
n
t
匀速直线运动
（4）如
a n
0,
a t
0；, 质点 c作
一般曲线运动
（5）如 a 0, a 0；, 质点c作
n
t
变速圆周运动
（6）如
a n
0,
a t
c；, 质点c作
匀变速圆周运动
（7）如 a 0, a 0；, 质点c作
dt dt
dt dt

大学物理切向、法向加速度

大学物理切向、法向加速度
contents
目录
• 切向加速度 • 法向加速度 • 切向、法向加速度的应用 • 切向、法向加速度的关联与区别 • 切向、法向加速度的实例分析
01 切向加速度
定义
01
02
03
切向加速度
描述物体在圆周运动或曲线运动中，沿运动轨迹切线方向的加速度。
切向加速度的大小
表示物体速度大小变化的快慢，单位为米每秒平方（m/s^2）。
物理意义
切向加速度的物理意义在于描述物体在曲线运动中速度大小的变
化趋势。
当切向加速度大于零时，物体速度大小增加；当切向加速度小于
零时，物体速度大小减小。
在匀速圆周运动中，切向加速度的大小表示物体在单位时间内速
度大小的变化量。
02 法向加速度
定义
法向加速度，也称为向心加速度，是指物体在圆周运动或曲线运动中，沿半径方向的加速度分量。
法向加速度与物体偏离轨道的方向有关，其方向与轨道半径垂直，大小表示物体偏离轨道的速度。
在曲线运动中，切向加速度和法向加速度的作用是不同的，切向加速度主要影响速度的大小，而法向加速
度则主要影响物体偏离轨道的方向。
05 切向、法向加速度的实例分析
匀速圆周运动中的切向、法向加速度
总结词
在匀速圆周运动中，切向加速度使物体保持匀速，而法向加速度使物体始终指向圆心。
曲线运动中的法向加速度
总结词
描述物体在曲线运动中的离心力效应。
详细描述
法向加速度主要描述物体在曲线运动中的离心力效应。当物体做曲线运动时，由于惯性作用，会产生一个指向曲率中心的力，即离心力。法向加速度的大小与物体的质量、曲率半径和线速度有关。

大学物理第一章第二节圆周运动与一般平面曲线运动

2、角加速度
lim
t 0 t
d
dt
d 2
dt 2
方向？
四、圆周运动中线量和角量的关系 1、线速度与角速度 v R
角速度的方向:
按“右旋规则”确定角加速度的方向: 加速时与方向相同减速时与方向相反
y
R
o
x
2、切向加速度与角加速度 3、法向加速度与角速度
a R
an
v2 R
v
R 2
4、速度分量式
（1）可将抛体运动分解为沿x和y 两个方向的独立运动。
立进行的运动迭加而成。
※
抛体运动方程的矢量形式
v
(v0cos )i
(v0
sin
gt)
j
v0t
r
1
gt
2
2
v dr dt
r
t vdt
0
t 0
(vxi
vy
j )dt
(v0t
cos
)i
(v0t
sin
1 2
gt2 )
j
（2）也可将抛体运动分解为沿初速度方向的匀速直线运动和
t
a a
ax2
a
2 y
R 2
7
五、匀变速率圆周运动
常量，故 at r，an r 2
dω 常量，
dt
又
dω dt d dt，
如 t 0 时, 0 ， 0
可得：
0 t θ θ0 0t
1 2
t
2
2
2 0
2 (
0)
匀变速率圆周运动
0 t
θ
θ0
0t
1 2
t

质点做圆周运动时,切向加速度和法向加速度产生的原因

质点做圆周运动时,切向加速度和法向加速度
产生的原因
质点做圆周运动时，其速度大小保持不变，但速度的方向在不断变化，这意味着质点具有加速度。

其中，切向加速度的产生原因是因为质点在作圆周运动时，速度方向的变化会导致速度的大小变化，而速度的大小变化就会产生切向加速度。

而法向加速度的产生原因，则是由于质点在做圆周运动时，其径向运动与切向运动不同步，导致质点与圆心之间的距离不断变化，从而产生法向加速度。

匀变速圆周运动切向加速度和法向加速度

合集下载

大学物理切向法向加速度.ppt

大学物理切向加速度和法向加速度

自然坐标系

切向加速度和法向加速度的数学表达式及其意义

大学物理3切向法向加速度

1-3切向加速度法向加速度

切向加速度和法向加速度课件

切向加速度和法向加速度

第 01章 2 次课 -- 加速度圆周运动

03运动学圆周运动 (自然坐标系、角速度、角加速度、切向加速度、法向加速度)

切向加速度和法向加速度

匀变速圆周运动切向加速度和法向加速度

大学物理12圆周运动

大学物理切向加速度和法向加速度

圆周运动的角量描述角量与线量的关系

大学物理第四章-刚体的转动-习题及答案

《大学物理》圆周运动

大学物理切向、法向加速度

大学物理第一章第二节圆周运动与一般平面曲线运动

质点做圆周运动时,切向加速度和法向加速度产生的原因

文档推荐

最新文档

匀变速圆周运动切向加速度和法向加速度

合集下载

大学物理切向法向加速度.ppt

大学物理切向加速度和法向加速度

自然坐标系

切向加速度和法向加速度的数学表达式及其意义

大学物理3切向法向加速度

1-3切向加速度法向加速度

切向加速度和法向加速度课件

切向加速度和法向加速度

第 01章 2 次课 -- 加速度 圆周运动

03运动学圆周运动 (自然坐标系、角速度、角加速度、切向加速度、法向加速度)

切向加速度和法向加速度

匀变速圆周运动切向加速度和法向加速度

大学物理12圆周运动

大学物理切向加速度和法向加速度

圆周运动的角量描述 角量与线量的关系

大学物理第四章-刚体的转动-习题及答案

《大学物理》圆周运动

大学物理切向、法向加速度

大学物理 第一章 第二节圆周运动与一般平面曲线运动

质点做圆周运动时,切向加速度和法向加速度产生的原因

文档推荐

最新文档

第 01章 2 次课 -- 加速度圆周运动

圆周运动的角量描述角量与线量的关系

大学物理第一章第二节圆周运动与一般平面曲线运动