多目标规划的原理和

基于多目标规划模型的建设方案优化设计概述：建设项目的规划和设计是一个复杂而关键的过程。

传统的规划方法往往只考虑单一目标，无法全面考虑各种因素的权衡和平衡。

而基于多目标规划模型的建设方案优化设计能够在考虑多个目标的基础上，找到最优解，提高建设方案的质量和效益。

一、多目标规划模型的概念和原理多目标规划模型是一种数学模型，它考虑了多个目标之间的相互关系和权衡。

在建设项目中，常见的目标包括经济效益、环境效益、社会效益等。

多目标规划模型的原理是通过建立目标函数和约束条件，将多个目标转化为数学问题，并利用数学方法求解最优解。

二、建设方案的多目标优化设计1. 目标的确定在进行多目标优化设计前，需要明确建设方案的各个目标。

例如，对于一个城市道路建设项目，目标可以包括减少交通拥堵、提高通行效率、降低能耗等。

目标的确定需要综合考虑项目的特点和需求，确保目标的合理性和可操作性。

2. 变量的选择变量是影响建设方案的因素，通过调整变量的取值可以改变建设方案的性能。

在多目标优化设计中，需要选择合适的变量，并确定其取值范围。

例如，对于道路建设项目，变量可以包括道路宽度、道路材料、交通信号灯等。

选择合适的变量可以提高优化设计的效果。

3. 目标函数的建立目标函数是多目标优化设计的核心，它反映了各个目标之间的关系和权衡。

在建立目标函数时，需要考虑目标之间的相互影响和权重。

例如，对于道路建设项目，可以建立一个综合评价指标，包括交通拥堵指数、通行效率指数和能耗指数。

通过设定不同的权重，可以实现不同目标之间的平衡。

4. 约束条件的设置约束条件是多目标优化设计的限制条件，它反映了建设方案的可行性和可操作性。

在设置约束条件时，需要考虑项目的实际情况和限制条件。

例如，对于道路建设项目，约束条件可以包括土地利用限制、环境保护要求等。

合理设置约束条件可以确保优化设计的可行性和可持续性。

5. 模型求解和结果分析通过建立多目标规划模型，可以利用数学方法求解最优解。

最优化多目标规划动态规划多目标规划是指在决策问题中同时考虑多个目标的优化问题，其目标可能相互矛盾或者相互关联。

动态规划是一种通过将问题划分为子问题并利用子问题的最优解来求解整体最优解的方法。

将多目标规划与动态规划结合起来，可以解决一些具有多个相互关联目标的决策问题。

下面将介绍最优化多目标规划动态规划的原理和应用举例。

1.定义决策变量：确定需要作出的决策，并定义决策变量。

2.建立状态转移方程：将问题划分为多个子问题，并建立它们之间的状态转移方程。

状态转移方程描述了子问题之间的关系，通过子问题之间的转移可以得到整体问题的最优解。

3.确定初始状态和边界条件：确定初始状态和边界条件，即子问题的初始状态和边界条件，用于递归地求解子问题。

4.递推求解：使用动态规划的递推求解方法，从初始状态开始，逐步求解子问题，直到求解出整体的最优解。

5.分析最优解：根据求解结果分析得到的最优解，并根据需要进行调整和优化。

假设有一家公司要进行产品的生产安排，公司有多个产品需要安排生产，每个产品有不同的生产时间和利润，同时公司还要考虑生产能力的限制和产品订单的要求。

问题可以建立如下的数学模型：决策变量：对于每个产品，决定其生产数量。

目标函数：最大化总利润。

约束条件：生产时间不能超过生产能力限制，同时生产数量要满足订单要求。

利用动态规划方法可以将问题分解为多个子问题，以子问题的最优解作为动态规划的递推依据。

具体步骤如下：1.将产品的生产时间和利润作为状态，根据时间顺序划分为多个子问题。

2.定义状态转移方程，将子问题的最优解与前面子问题的最优解关联起来。

3.初始状态为生产时间为0的情况，边界条件为订单要求。

4.递推求解，根据状态转移方程求解每个子问题的最优解。

5.分析最优解，确定每个产品的生产数量，以及总利润。

通过最优化多目标规划动态规划的方法，可以在满足多个目标和约束条件的情况下，求解出最优的决策方案。

这种方法可以应用于生产调度、资源分配、物流配送等领域，帮助企业做出合理的决策，达到优化目标。

多目标规划模型及其在生产优化中的应用随着科技的不断进步，企业在生产的过程中需要考虑的因素也越来越多，例如成本、质量、效率、环保等多个方面。

这些因素不仅对企业的发展起到了决定性的作用，而且对于整个行业的发展也具有重要意义。

因此，在这个时代，如何能够完成多目标规划，对于企业的生产优化是非常重要的。

本文将从多目标规划模型及其在生产优化中的应用方面进行探讨。

一、多目标规划模型的概述多目标规划（multi-objective programming，MOP）是指在满足多个目标的基础上，寻求最优方案的一种决策方法。

多目标规划模型是通过建立目标函数，对每个目标进行评价和权衡，从而实现多目标的决策优化模型。

多目标规划模型可以被用来解决许多现实生产和决策问题，例如资源配置问题、供应链管理问题、营销决策问题、风险管理和环境保护问题等等。

在这些问题中，优化目标多个，且有时目标之间存在着矛盾性，因此需要采用多目标规划模型来解决。

二、多目标规划模型在生产优化中的应用1. 降低成本和提高质量对于一个企业来说，成本和质量是两个非常重要的因素。

如何同时降低成本和提高质量成为了企业的一个难题。

多目标规划模型可以帮助企业在进行生产决策时，考虑多个目标，实现成本和质量的平衡。

在多目标规划模型中，建立成本和质量的目标函数，对企业的各项指标进行量化和分析，然后对目标函数进行加权，最终得到最优方案。

通过这种方式，企业可以在不降低产品质量的条件下，实现成本的降低，从而提高企业的效益。

2. 提高生产效率和降低能耗随着市场竞争的加剧，企业需要不断提高生产效率，从而降低成本，并提高企业的竞争力。

另一方面，环境保护也成为了现代企业生产的一个必须考虑的因素。

多目标规划模型可以在生产过程中，同时考虑生产效率和能耗，实现生产的可持续发展。

在多目标规划模型中，建立生产效率和能耗的目标函数，评估企业的各项指标，加权得到最优方案。

通过这种方式，企业可以在提高生产效率的同时，降低能耗，实现生产效率与环境保护的双赢。

第四章 多目标规划模型多目标决策问题的理论基础之一是向量优化问题，也称多目标优化问题。

这类问题，从方法论的角度看，它是一个目标函数中具有向量值的数学规划问题；从决策论角度看，它又是决策规则中含有各个目标极值的决策问题。

因此，多目标决策问题属于向量优化问题。

向量优化问题的解与标量优化问题的解是不同的。

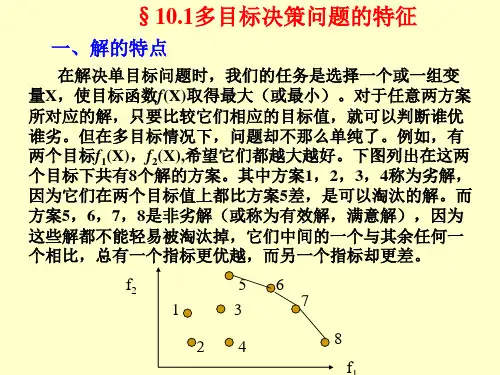
标量优化问题对任何两个函数的解，只要比较它们的两个函数值的大小，总可以从中找出一个最优解，且能排出它们的顺序；而多目标优化问题的解都是非劣解，且不是唯一的，究竟谁优谁劣，很难直接作出判断。

非劣解的概念是由经济学家pareto 于1896年提出的。

但是发展为向量优化问题的生成非劣解技术，还是在1951年Kuhn-Tucker 非劣性条件发表以后的事。

由于向量优化问题是在标量优化问题的基础上发展起来的，只要通过适当的途径将向量优化问题转化为标量优化问题，就可以利用求解标量优化问题的现有方法，求解具有一定特征的向量优化问题。

本章主要介绍有关向量优化问题的基本理论，如非劣解概念，特征非裂解的标量优化解法及非劣性的充要条件。

其中提到的许多概念和术语，在本书的后继章节中都是很有用的。

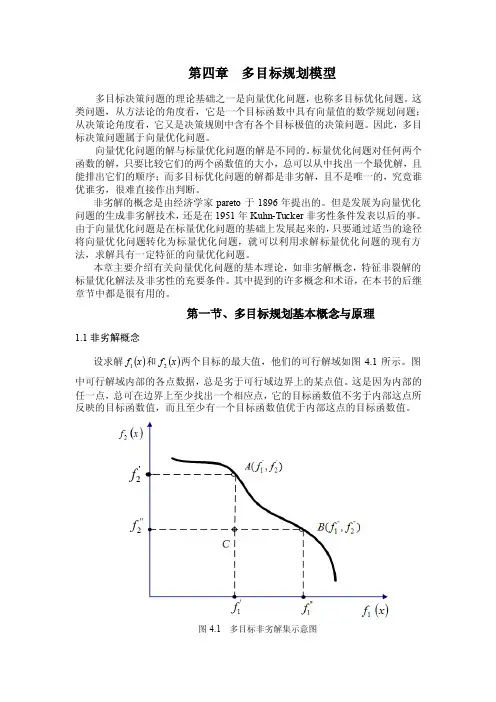
第一节、多目标规划基本概念与原理1.1非劣解概念设求解()x f 1和()x f 2两个目标的最大值，他们的可行解域如图4.1所示。

图中可行解域内部的各点数据，总是劣于可行域边界上的某点值。

这是因为内部的任一点，总可在边界上至少找出一个相应点，它的目标函数值不劣于内部这点所反映的目标函数值，而且至少有一个目标函数值优于内部这点的目标函数值。

图4.1 多目标非劣解集示意图例如，图中的C 点就劣于A 点和B 点之间任一点所反映的目标函数值。

所以，在优选中类似C 点的一些点可以舍去，并将这些可以舍去的解称为劣解。

但是可行域边界上各点所代表的解，就不能直接判断它们的优劣（如A 点、B 点就是这样）。

因为这些点中任一个与其他任一个相比较，总会发现一个目标函数值比其他另一个函数值优越，但又不是两个目标函数值都优越，否则其中的一个作为劣解而舍去。

单目标规划和多目标规划的区别与联系1.最优化概念最优化是应用数学的一个重要分支，最优化可定义为一种数学方法，用它可以对各种生产活动进行规划，在可供利用资源(资源泛指矿藏、水能、人力、设备、原料、运输条件、生态环境、资金、时间、空问等等)的限制条件下，使生产活动得到最大的效益或用最少的资源完成指定的生产活动。

最优化问题的数学表现形式为：式中，123()n f x x x x ⋅⋅⋅、、称为目标函数，若具体问题是求123max ()n f x x x x ⋅⋅⋅、、，则令123123()()n n x x x x f x x x x ϕ⋅⋅⋅=-⋅⋅⋅、、、、，于是最大值问题就转化为最小值问题123min ()n x x x x ϕ⋅⋅⋅、、。

123()j n h x x x x ⋅⋅⋅、、称为等式约束条件，123g ()i n x x x x ⋅⋅⋅、、称为不等式约束条件，如果约束条件中有123()0i n s x x x x ⋅⋅⋅≤、、，则可令123123()g ()i n i n s x x x x x x x x ⋅⋅⋅=-⋅⋅⋅、、、、，于是原来的“≤”就变为了“≥”。

满足约束条件的一组123n x x x x ⋅⋅⋅、、称之为一组可行解。

满足目标函数的可行解称为最优解，即我们需要寻求的答案。

许多现实和理论问题都可以建模成这样的一般性框架，最优化问题种类繁多，分类的方法也有许多。

按目标函数的个数分类：1）单目标规划:只存在一个目标函数时，称这一类问题为单目标规划。

2）多目标规划：当存在多个目标函数时，称为多目标规划。

2.单目标规划方法非线性规划问题的求解一般要比线性规划困难很多，而且目前尚没有适合于各类非线性问题的一般算法，每种算法都有自己的特定的使用范围。

有些情况下，为方便计算，也会把非线性规划问题近似为线性规划问题进行求解。

2.1一维搜索一维搜索是求解单变量非线性规划问题的方法。

这类方法不仅有实用价值，而且大量多维最优化方法都依赖于一系列的一维最优化。

多目标规划模型
多目标规划模型是一种求解多个目标总体最优支线的LPP模型，旨在完成多个相关目
标最优满足。

包括经济、社会和环境等专业特性有利于避免单项过度追求，全面评估系统
最佳性能，它也称为混合目标规划或复杂目标规划模型。

构建一个多目标规划模型的方法应该从以下几个方面展开：
首先，应该根据求解问题的特点，确定多目标case的目标函数类型，并定义各个目
标函数。

其次，明确多目标case的约束条件，即求解问题实际具有的各种条件，如限制条件、限制条件等。

接着，根据多目标规划模型的定性要求，选择满足各个目标函数的优化算法，建立求
解模型。

总的来说，多目标规划模型具有明确的定性优化要求，长远地满足多个相关目标最优
满足，被应用于经济、社会和环境等各个领域。

其优点在于，在实际社会经济中，多目标
规划模型可以有效弥补传统的单目标规划模型的不足，完善单项过度追求的问题，以及全
面考核系统的最佳性能。

多目标规划的若干理论和方法共3篇多目标规划的若干理论和方法1多目标规划的若干理论和方法多目标规划是指在多目标条件下进行决策的一种数学方法，它把一个问题转化成一个具有多个目标约束条件的数学优化问题。

在现代化的社会经济发展中，人们往往不仅仅关注单一的目标，而是有着多种不同的目标和需求。

因此，多目标规划技术应运而生，被广泛应用于各行各业的决策和管理中。

本文将简单介绍多目标规划的若干理论和方法。

一、多目标规划的相关理论1. Pareto最优解Pareto最优解是多目标规划中比较重要的概念之一，它指的是在多个目标之间不能再做出更好的妥协的一种解法。

具体来说，如果一个解决方案比其他所有解决方案在某个目标上优秀，而在其他目标上没有任何明显的劣势，则该解决方案就被称为Pareto最优解。

2. 支配支配是另一个多目标规划的重要概念，它指的是在所有可能的解空间中，一个解决方案中所有目标值都比另一种解决方案好，则前者支配后者。

例如，如果一个解决方案在所有目标上都比另一个解决方案好，则前者支配后者。

3. 目标规划多目标规划中，一个重要的理论发展就是目标规划。

它把问题分解为多个聚焦于更少数目标的小问题。

通过优化多个小问题的解决方案，最终达到全局最优解。

二、多目标规划的方法1. 权值法权值法是多目标规划的一种基础方法，其主要思路是通过对每个目标进行加权求和，将多目标问题转化为单一目标问题。

先确定每个目标的权重，然后将所有目标的得分加权求和，得到唯一的一个综合得分。

由此作为参考，进一步进行优化。

2. 线性规划法线性规划法是一种基础的多目标规划方法，它的求解过程基于线性规划。

将所有的目标约束转为线性规划约束条件，然后通过线性规划问题来求解最优解。

3. 模糊规划法模糊规划法是一种基于模糊数学的多目标规划方法。

它采用模糊数值来表达目标和约束条件，并通过模糊方法解决多目标策略问题。

4. 遗传算法遗传算法是一种基于生物进化原理的求解多目标规划问题的方法。