2012江苏省数学竞赛《提优教程》教案：第33讲__周期函数与周期数列

第11讲 数列的求和本节主要内容有S n 与a n 的关系；两个常用方法：倒写与错项；各种求和：平方和、立方和、倒数和等；∑符号的运用. 掌握数列前n 项和常用求法,数列求和的方法主要有：倒序相加法、错位相减法、转化法、裂项法、并项法等． 1.重要公式①1+2+…+n =21n (n +1) ②12+22+…+n 2=61n (n +1)(2n +1)③13+23+…+n 3=(1+2+…+n )2=41n 2(n +1)22.数列{a n }前n 项和S n 与通项a n 的关系式：a n =⎩⎨⎧≥-=-2,1,11n S S n S n n3. 在等差数列中S m +n =S m +S n +mnd,在等比数列中S m +n =S n +q n S m =S m +q m S n ．4.裂项求和：将数列的通项分成两个式子的代数和，即a n =f (n +1)－f (n )，然后累加时抵消中间的许多项．应掌握以下常见的裂项：等)!1(1!1)!1(1④,ctg2ctg 2sin 1③,!)!1(!②,111)1(1①+-=+-=α-+=⋅+-=+n n n ααn n n n n n n n 5.错项相消法6.并项求和法A 类例题例1 已知数列｛a n ｝的通项公式满足：n 为奇数时，a n =6n －5 ，n 为偶数时，a n =4 n ，求s n . 分析 数列｛a n ｝的前n 项可分为两部分，一部分成等差数列，用等差数列求和公式；另一部分成等比数列，用等比数列求和公式。

但数列总项数n 的奇偶性不明，故需分类讨论. 解 若n 为偶数2m ，则S 2m =1+13+25+…+[6(2m －1)－5]+42+44+…+42m =6m 2－5m+1615(42m－1)， S n =23516(41)2215n n n -+-. 若n 为奇数2m+1时，则S 2m+1=S 2m +6(2m+1)－5=6m 2+7m+1+1615(42m－1)， S n =21313114221515n n n ++-+⋅. 说明 如果一个数列由等差数列与等比数列两个子数列构成，常采纳先局部后整体的策略，对子数列分别求和后，再合并成原数列各项的和.类似地，若一个数列的各项可拆成等差数列型与等比数列型两部分，也可采纳先局部后整体的策略.例2(2004年湖南卷类) 已知数列{a n }是首项为a 且公比q 不等于1的等比数列，S n 是其前n 项的和，a 1，2a 7，3a 4 成等差数列．（I ）证明 12S 3，S 6，S 12－S 6成等比数列； （II ）求和T n =a 1+2a 4+3a 7+…+n a 3n －2．分析 (1)对于第(l)问，可先依据等比数列的定义与等差数列的条件求出等比数列的公比，然后写出12S 3，S 6，S 12－S 6，并证明它们构成等比数列．对于第(2)问，由于 T n =a 1+2a 4+3a 7+…+n a 3n －2．所以利用等差数列与等比数列乘积的求和方法即“乘公比错位相减法”解决此类问题．解 （Ⅰ）证明 由4713,2,a a a 成等差数列， 得41734a a a +=，即 .3436aq a aq += 变形得 ,0)1)(14(33=-+q q 所以14133=-=q q 或（舍去）．由 .1611211)1(121)1(123316136=+=----=q qq a q q a S S.1611111)1(1)1(166611216126612==-+=-----=-=-q q qq a q q a S S S S S 得.12661236S S S S S -= 所以12S 3，S 6，S 12－S 6成等比数列． （Ⅱ）解：.3232)1(36323741--++++=++++=n n n naq aq aq a na a a a T即 .)41()41(3)41(212a n a a a T n n --⋅++-⋅+-⋅+= ①①×)41(-得： a n a n a a a T n n n )41()41()41(3)41(24141132---⋅++-⋅+-⋅+=--.)41()54(54)41()41(1])41(1[a n a a n a n n n -⋅+-=-⋅-----=所以 .)41()542516(2516a n a T n n -⋅+-=说明 本题是课本例题：“已知S n 是等比数列{a n }的前n 项和，S 3，S 9，S 6成等差数列，求证：a 2，a 8，a 5成等差数列”的类题，是课本习题：“已知数列{an}是等比数列，S n 是其前 n 项的和，a 1，a 7，a 4 成等差数列，求证2 S 3，S 6，S 12－S 6成等比数列”的改编．情景再现1．(2000年全国高考题)设{}n a 为等比数例，n n n a a a n na T ++-+=-1212)1( ，已知11=T ，42=T ．（Ⅰ）求数列{}n a 的首项和公式；（Ⅱ）求数列{}n T 的通项公式．2． (2000年全国高中数学联赛)设S n =1+2+3+…+n ,n ∈N ，求f (n )=1)32(++n nS n S 的最大值.B 类例题例3 (2004年重庆卷) 设),2,1(,3235,35,11221 =-===++n a a a a a n n n （1）令1,(1,2......)n n n b a a n +=-=求数列{}n b 的通项公式；（2）求数列{}n na 的前n 项和n S .分析 利用已知条件找n b 与1+n b 的关系,再利用等差数列与等比数列之积的错位相差法来解决此类问题.解 （1）因121+++-=n n n a a b n n n n n n b a a a a a 32)(323235111=-=--=+++ 故{b n }是公比为32的等比数列，且故,32121=-=a a b ),2,1()32( ==n b n n（2）由得n n n n a a b )32(1=-=+)()()(121111a a a a a a a a n n n n n -++-+-=--++])32(1[232)32()32()32(21n n n -=++++=- 注意到,11=a 可得),2,1(3231 =-=-n a n nn记数列}32{11--n n n 的前n 项和为T n ，则1832)3()1(232)21(3232)3(9)32(3])32(1[9,)32(])32(1[3)32()32()32(32131)2()32()32(23232),1()32(3221112111221-+++=-+++=+++=+-=--=--=-++++=⋅++⋅+=⋅++⋅+=-+---n n n n n n n nn n nn n n n n n n n n n n T n na a a S n n T n n T n T n T 从而故两式相减得说明 本题主要考查递推数列、数列的求和，考查灵活运用数学知识分析问题和解决问题的能力. 例4 (1996年全国高中数学联赛第二试)设数列{a n }的前项和S n =2a n －1(n=1,2,3, )，数列{b n }满足b 1=3, b k+1=a k +b k (k=1,2,3 ).求数列{b n }的前n 项和. 分析 由数列{a n }前n 项和S n 与通项a n 的关系式：a n =⎩⎨⎧≥-=-2,1,11n S S n S n n 可得a n.解 由12-=n n a S 可得a n+1=2a n 即数列{a n }是等比数列,故a n =2n －1,又由a k =b k+1－b k得b n =b 1 +a 1+ a 2+ a 3+…+ a n －1 =3+12121---n =221+-n所以S n =b 1+ b 2+ b 3+…+ b n =1+2+22+…+2n －1+2n=12221221-+=+--n n n n例5 (2004年全国理工卷) 已知数列{a n }的前n 项和S n 满足：S n =2a n +(－1)n ,n ≥1.(1)写出求数列{a n }的前3项a 1,a 2,a 3；(2)求数列{a n }的通项公式； (3)证明：对任意的整数m >4，有4511178m a a a +++<. 分析 由数列{a n }前n 项和S n 与通项a n 的关系,求a n ,应考虑将a n 与a n -1或 a n+1其转化为的递推关系,再依此求a n. 对于不等式证明考虑用放缩法,若单项放缩难以达到目的,可以尝试多项组合的放缩.解 (1)当n =1时,有：S 1=a 1=2a 1+(－1)⇒ a 1=1；当n =2时,有：S 2=a 1+a 2=2a 2+(－1)2⇒a 2=0； 当n =3时,有：S 3=a 1+a 2+a 3=2a 3+(－1)3⇒a 3=2； 综上可知a 1=1,a 2=0,a 3=2；(2)由已知得：1112(1)2(1)n n n n n n n a S S a a ---=-=+----化简得：1122(1)n n n a a --=+-上式可化为：1122(1)2[(1)]33n n n n a a --+-=+-故数列{2(1)3n n a +-}是以112(1)3a +-为首项, 公比为2的等比数列.故121(1)233n n n a -+-= ∴121222(1)[2(1)]333n n n n n a --=--=--数列{n a }的通项公式为：22[2(1)]3n n n a -=--. ⑶由已知得：232451113111[]221212(1)m mm a a a -+++=+++-+-- 23111111[]2391533632(1)m m-=++++++--11111[1]2351121=+++++11111[1]2351020<+++++511(1)1452[]12312m --=+-514221[]23552m -=+- 51311131041057()1552151201208m -=-<=<=. 故4511178m a a a +++<( m >4). 说明 本题是一道典型的代数综合题，是将数列与不等式相结合，它的综合性不仅表现在知识内容的综合上，在知识网络的交汇处设计试题，更重要的是体现出在方法与能力上的综合，体现出能力要素的有机组合．虽然数学是一个演绎的知识系统，并且演绎推理是数学学习和研究的重要方法，但从数学的发展来看，“观察、猜测、抽象、概括、证实”是发现问题和解决问题的一个重要途径，是学生应该学习和掌握的，是数学教育不可忽视的一个方面：要求应用已知的知识和方法，分析一些情况和特点，找出已知和未知的联系，组织若干已有的规则，形成新的高级规则，尝试解决新的问题，这其中蕴含了创造性思维的意义．例 6 设{ a n }为等差数列，{ b n }为等比数列，且211a b =,222a b = ,233a b =,又12lim()2n x b b b →∞+++=, 试求{ a n }的首项与公差． (2001年全国高中数学联赛) 分析 题中有两个基本量{ a n }中的首项 a 1 和公差d 是需要求的，利用21a ,22a ,23a 成等比数列和给定极限可列两个方程，但需注意极限存在的条件． 解 设所求公差为d ，∵a 1＜a 2，∴d ＞0．由此得 412121)()2(d a d a a +=+ 化简得：0422121=++d d a a 解得：1)22(a d ±-= 而022<±-，故a 1＜0若1)22(a d --=，则22122)12(+==a a q若1)22(a d +-=，则22122)12(-==a a q但12)(21+=++++∞→n n b b b lim 存在，故| q |＜1，于是2)12(+=q 不可能．从而2)12)(222(12)12(121221=+-=⇒+=--a a所以222)22(,211-=+-=-=a d a说明 本题涉及到的知识主要是等差数列、等比数列、无穷递缩等比数列所有项的和等知识，用到方程的思想和方法，且在解题过程中要根据题意及时取舍，如由题意推出d ＞0， a 1＜0，1<q 等，在解题中都非常重要．情景再现3． 设二次函数)(,*)](1,[,)(2x f N n n n x x x x f 时当∈+∈+=的所有整数值的个数为g(n). （1）求g(n)的表达式.（2）设.,)1(*),()(321432123n n n n n S a a a a a S N n n g n n a 求--++-+-=∈+=（3）设l Z l l T b b b T n g b n n n nn 求若),(.,2)(21∈<+++==的最小值. 4． 设函数222)(+=x xx f 的图象上两点P 1(x 1，y 1)、P 2(x 2，y 2)，若)(2121OP OP +=，且点P 的横坐标为21． (1)求证：P 点的纵坐标为定值，并求出这个定值；(2)若∑==ni n ni f S 1)(，n ∈N *，求S n ；(3)记T n 为数列})2)(2(1{1+++n n S S 的前n 项和，若)2(1+<+n n S a T 对一切n ∈N *都成立，试求a 的取值范围．C 类例题例7 给定正整数n 和正数M ，对于满足条件2121++n a a ≤ M 的所有等差数列a 1，a 2，…，a n ，，试求S=a n+1+a n+2+…+a 2n+1的最大值． (1999年全国高中数学联赛试题)分析 本题属于与等差数列相关的条件最值问题，而最值的求解所运用的方法灵活多样，针对条件的理解不同，将有不同的解法．解 (方法一)：设公差为d, a n+1=a .则S=a n+1+a n+2+…+a 2n+1=d n n a n 2)1()1(+++,所以12+=+n Snd a 另一方面,由M ≥2121++n a a =22)(a nd a +-=22)34(1012104nd a nd a -+⎪⎭⎫ ⎝⎛+=21104⎪⎭⎫ ⎝⎛+n S ,从而有M n S ⋅+≤)1(210且当nMd M a ⋅=⋅=104,103时 )1(+=n S ⎪⎪⎭⎫ ⎝⎛⋅⋅+⋅n M n M 1042103=M n 105)1(⋅+M n )1(210+=, 由于此时nd a 34=故2121++n a a =21104⎪⎭⎫⎝⎛+n S =M,因此S=a n+1+a n+2+…+a 2n+1的最大值为M n )1(210+． (方法二)：三角法 由条件2121++n a a ≤ M 故可令θ=cos 1r a ,θ=+sin 1r a n ,其中M r ≤≤0.故S= a n+1+a n+2+…+a 2n+1=2)1)((121++++n a a n n )3(2111a a n n -+=+ )cos sin 3(21θ-θ+=r n)sin()1(210ϕ-θ+=r n 其中103cos =ϕ,101sin =ϕ因此当1)sin(=ϕ-θ,M r =时,S=a n+1+a n+2+…+a 2n+1的最大值为M n )1(210+．说明 在解答过程中，要分清什么是常量，什么是变量，注意条件和结论的结构形式．解法一通过配方来完成，解法二运用三角代换的方法，解法三运用二次方程根的判别式来完成，解法四则主要运用了柯西不等式．本题人口宽，解法多样，对培养学生的发散思维能力很有好处．例8 n 2(n ≥4)个正数排成几行几列：a 11 a 12 a 13 a 14 … a 1n ， a 21 a 22 a 23 a 24 … a 2n ， a 31 a 32 a 33 a 34 … a 3n ， … …a n1 a n2 a n3 a n4 … a n n ，其中每一行的数成等差数列，每一列的数成等比数列，并且所有公比相等，已知“a 24=1， a 42 81, a 43163=, 求a 11 +a 22 +a 33 +…+ a nn . (1990年全国高中数学联赛试题)分析 由于等差数列可由首项与公差惟一确定，等比数列可由首项与公比惟一确定，如果设a 11=a 第一行数的公差为d ，第一列数的公比为q ，容易算得a s t =[a+(t －1)]q s －1，进而由已知条件，建立方程组，求出n ，d ，q ．解 设第一行数列公差为d ，各列数列公比为q ，则第四行 数列公差是dq 2.于是可得方程组：⎪⎪⎪⎩⎪⎪⎪⎨⎧=+==+==+=16381)(1)3(34243311421124dq a a q d a a q d a a ,解此方程值组,得2111±===q d a .由于所给n 2个数都是正数,故必有q ＞0,从而有2111===q d a . 故对任意1≤k ≤n,有)]1([1111-+==-k a q a a k k kk kk k q 21=-. 故S=21+222+323+…+n n 2. 又21S=221+322+423+…+12+n n . 两式相减后可得： 21S=21+222+323+…+n n 212+-n n所以S=2－121-n －n n 2. 说明 这道试题涉及到等差数列、等比数列、数列求和的有关知识和方法．通过建立方程组确定数列的通项；通项确定后，再选择错位相减的方法进行求和．情景再现5．各项为实数的等差数列的公差为4，其首项的平方与其余各项之和不超过100，这样的数列至多有 项．6．己知数列{a n }满足：a 1=1,a n+1=a n +1a n(1)求证:14＜ a 100＜ 18; (2)求a 100的整数部分[a 100].习题11A 类习题1.若等差数列{a n }，{b n }的前n 项和分别为A n ，B n ，且A n B n = 7n +14n +27 ，则a 11b 11等于 （ ）A ． 43B ． 74C ． 32D ． 78712.各项均为实数的等比数列{a n }前n 项和记为S n ，若S 10=10,S 30=70，则S 40等于 ( )A.150B.－200C.150或－200D.400或－50 (1998年全国高中数学联赛试题)3.已知数列{}a n 满足)1(431≥=++n a a n n ,且91=a ,其前n 项之和为S n ,则满足不等式1251|6|<--n S n 的最小整数n 是 ( )A.5B. 6C.7D.8 (1999年全国高中数学联赛试题)4.(2004年江苏卷)设无穷等差数列{a n }的前n 项和为S n ． (Ⅰ)若首项=1a 32 ，公差1=d ，求满足2)(2k k S S =的正整数k ；(Ⅱ)求所有的无穷等差数列{a n }，使得对于一切正整数k 都有2)(2k k S S=成立．5．函数f x ()是定义在［0，1］上的增函数，满足)2(2)(x f x f =且1)1(=f ，在每个区间]21,21(1-i i （i =1，2……）上，y f x =()的图象都是斜率为同一常数k 的直线的一部分． （I ）求)0(f 及)21(f ，)41(f 的值，并归纳出),2,1)(21( =i f i 的表达式 （II ）设直线i x 21=，121-=i x ，x 轴及y f x =()的图象围成的矩形的面积为a i （i =1，2……），记)(lim )(21n n a a a k S +++=∞→ ，求S k ()的表达式，并写出其定义域和最小值. (2004年北京理工卷)6.(2005年湖北卷)设数列}{n a 的前n 项和为S n =2n 2，}{n b 为等比数列，且.)(,112211b a a b b a =-=（Ⅰ）求数列}{n a 和}{n b 的通项公式； （Ⅱ）设nnn b a c =，求数列}{n c 的前n 项和T n . B 类习题7．(2005年全国Ⅰ卷)设正项等比数列{}n a 的首项211=a ，前n 项和为n S ，且0)12(21020103010=++-S S S ．（Ⅰ）求{}n a 的通项；（Ⅱ）求{}n nS 的前n 项和n T ．8.设数列{a n }的首项a 1=1，前n 项和S n 满足关系式：3tS n －(2t +3)S n －1=3t (t ＞0,n =2,3,4…). (1)求证：数列{a n }是等比数列；(2)设数列{a n }的公比为f (t )，作数列{b n }，使b 1=1,b n =f (11-n b )(n =2,3,4…)，求数列{b n }的通项b n ；(3)求和：b 1b 2－b 2b 3+b 3b 4－…+b 2n －1b 2n －b 2n b 2n +1. 9.已知：f(x)＝412-x （x<—2），f(x)的反函数为g(x),点An(a n ,11+-n a )在曲线y ＝g(x)上(n ∈N +)，且a 1＝1.（I ）求y ＝g(x)的表达式；（II ）证明数列{21na }为等差数列；（Ⅲ）求数列{a n }的通项公式；（Ⅳ）设b n ＝1111++n n a a ,记S n ＝b 1＋b 2＋……＋b n ，求S n .10.已知正整数n 不超过2000，并且能表示成不少于60个连续正整数之和，那么，这样的n 的个数是_____.(1999年全国高中数学联赛试题)C 类习题11．已知}{n a 是首项为2，公比为21的等比数列，n S 为它的前n 项和． （1）用n S 表示1+n S ；（2）是否存在自然数c 和k ，使得21>--+cS cS k k 成立． (2001年上海卷)12．数列{a n }是首项为a 1，公差为d 的等差数列，按下列加括号的方式把该数列分成群(a 1)、( a 2，a 3)、( a 4，a 5，a 6，a 7)、( a 8，a 9，a 10，…，a 15)…使第一群中是a 1含{a n }中的一项，第二群是a 2、a 3，含{a n }中的两项，第三群中是a 4、a 5、a 6、a 7，含{a n }中的四项…如此继续下去，第n 群中含{a n }中的2n －1项，且任两群无公共项，任一项都在某群内，用a 1、d 、n 表示第n 群各元素的和. (第2届希望杯第一试) 本节“情景再现”解答：1．设等比数列{}n a 以比为q ，则)2(2,121211q a a a T a T +=+==．∵4,121==T T ，∴2,11==q a ． （Ⅱ）解法一：由（Ⅰ）知2,11==q a ，故1112--==n n n q a a ，因此，1221222)1(1--⋅+⋅++⋅-+⋅=n n n n n T ，22- 21222-2222 ]21222)1(1[- 21222)1(221121-n 212-+=-⋅+=+++++=⋅+⋅++⋅-+⋅⋅+⋅++⋅-+⋅=-=∴+---n nnn n n n n n n n -n -n n n n n T T T12)2(+++-=n n ．解法二：设n n a a a S +++= 21．由（Ⅰ）知12-=n n a ．∴122211-=+++=-n n n S2221222222121212 S )()(a 2)1(121121211121n n )-n () -()-()(S S a a a a a a a a a n na T n n nnnnn n n n n n --=--⋅-=+++=++++=+++=++++++++=+++-+=∴+-- 2．由等差数列求和公式得 )1(21+=n n S n ， 11(1)(2)2n S n n +=++ ∴ 1)32()(++=n n S n S n f ＝64342++n n n ＝n n 64341++＝50)8(12+-nn 501≤, ∴ 当 88-n ，即n ＝8时，501)(m ax =n f . 3．（1）当*)](1,[N n n n x ∈+∈时，函数x x x f +=2)(的值随x 的增大而增大，则)(x f 的值域为*).](23,[22N n n n n n ∈+++ ∴*).(32)(N n n n g ∈+=（2）.)(32223n n g n n a n =+= ①当n 为偶数时，])1[()43()21(22222214321n n a a a a a a S n n n --++-+-=-++-+-=-=－[3+7+……+（2n －1）]=－.2)1(22)12(3+-=⋅-+n n n n ②当n 为奇数时，n n n n n a S a a a a a a S +=-++-+-=---1124321)()()(=－.2)1(2)1(2+=+-n n n n n ∴.2)1()1(1+-=-n n S n n （3）由nn n nn n n T n g b 232212292725,2)(132+++++++==- 得, ① ①×21，得.232212272521132+++++++=n n n n n T ② ①－②，得)222222()23225(21321n n n n T +++++-=+ =.27227211)211(21)23225(111+-++-=--++-n n n n n∴.2727n n n T +-= 则由Z l l n T nn∈<+-=,2727，可得l 的最小值是7. 4． (1)证：∵)(2121OP OP OP +=，∴P 是P 1P 2的的中点 ⇒ x 1＋x 2＝1， ∴222222222222)()(11111122112121+++=+++=+=+--x x x x x x x x x f x f y y 1=2+22+2+22=2×2+22+2+22=111111x x x x x x ，∴21)(2121=+=y y y p . (2)解：由(1)知x 1＋x 2＝1，f (x 1)＋f (x 2)＝y 1＋y 2＝1，f (1)＝2－2，S n = f( 1n ) + f( 2n ) + ┅ + f( n －1n ) + f( nn )，又S n = f( n n ) + f( n －1n ) + ┅ + f( 2n )+ f( 1n)，两式相加得2S n = f(1) + [f( 1n ) + f( n －1n )] + [f( 2n ) + f( n －2n )] + ┅ + [f( n －1n ) + f( 1n )] + f(1)= 2f(1) + 1 + 1 + ┅ + 1(n －1个1)223-+=n ， ∴2223-+=n S n ．(3)解：)4131(4)4)(3(4221)2)(2(11+-+=++=⋅=+++n n n n S S n nT n = 4[(14 －15 ) + (15 －16 ) + ┅ + (1n + 3 －1n + 4 )] = nn + 4 ， )2(1+<+n n S a T ⇔82)4(2221++=+=+>+nn n n S T a n n ，∵n n 16+≥8，当且仅当n ＝4时，取“＝”， ∴818828162=+≤++nn ，因此，81>a ． 5． 设n a a a ,,,21 是公差为4的等差数列,则)1(41-+=n a a n ,由已知 100221≤+++n a a a ⇔1002)1)(4(121≤-+++n a a a n⇔ 010022)1(2121≤--+-+n n a n a ,此关于1a 为未知数的一元二次不等式有解,则应有0)10022(4)1(22≥----=∆n n n⇔7n 2―6n ―401≤0,9728163728163<+≤≤-n 又8728163>+ 故n 的最大值是8. 故这样的数列至多有8项．6．(1)证明:当1＜ k ≤n( k ∈ N*)时,=2k a 212112--++k k a a 且a k ＞1所以3221221+<<+--k k k a a a ,因此32232221+<<+a a a ,32242322+<<+a a a ,………,3221221+<<+--n n n a a a ,将以上n- 1个式子相加得)1(3)1(221221-+<<-+n a a n a n ,因为a 1=1所以23122-<<-n a n n ,所以2312-<<-n a n n令n=100,得14＜ a 100＜ 18.(2)由题设得222112n n n a a a +=-+, 所以2100a =+21a +-)(2122a a +-)(2223a a …+)(2992100a a -=200+[+221a +231a + (299)1a ],又a n+1-a n =1a n ＞0故数列{a n }是单调递增.当n ≥2时a n ≥2. 200＜2100a ＜200+5.22498212=⨯⎪⎭⎫⎝⎛＜225.因此14＜ a 100＜15.所以a 100的整数部分[a 100]=14本节“习题11”解答：1． a 11b 11 =2a 112b 11 =a 1 +a 21b 1 +b 21 =21×2+21×2+211211b b a a =A 21B 21 = 7×21+14×21+27 =43 故选A. 2．S 10, S 20－S 10, S 30－S 20,S 40－S 30成等比数列,公比Q=q 10>0.故S 30= S 10(1+Q+Q 2)=70.解得Q=2,所以S 40－S 30=S 10Q 3=80,即S 40=S 30+80=150. 故选A.3．由递推公式变形得：3(a n+1－1)=－(a n －1)令b n =a n －1,则b n+1=－13b n ,且b 1=a 1－1=8,故 {b n }是首项为8,公比为－13的等比数列.故S n －n=(a 1－1)+ (a 2－1)+…+ (a n －1)= b 1+b 2++…+b n =3113111+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--n b =6－6×n ⎪⎭⎫ ⎝⎛-31,所以1251316|6|<⎪⎭⎫ ⎝⎛⨯=--nn n S , 得3n －1>250.所以满足不等式的最小整数n 是7,故选C. 4．（1）当1,231==d a 时，n n n n n S n +=-+=2212)1(23，由2)(2k k S S =得，2224)21(21k k k k +=+ ，即0)141(3=-k k ，又0≠k ，所以4=k ． （2）设数列{}n a 的公差为d ，则在2)(2k k S S =中分别取2,1=k 得⎩⎨⎧==224211)()(S S S S 即⎪⎩⎪⎨⎧⨯+=⨯+=211211)2122(2344 d a d a a a ，由（1）得01=a 或11=a ． 当01=a 时，代入（2）得：0=d 或6=d ；当0,01==d a 时，0,0==n n S a ，从而22)(k k S S =成立；当6,01==d a 时，则)1(6-=n a n ，由183=S ，216,324)(923==S S 知，239)(S S ≠，故所得数列不符合题意；当11=a 时，0=d或2=d ，当11=a ，0=d 时，n S a n n ==,1，从而22)(k k S S =成立；当11=a ， 2=d 时，则2,12n S n a n n =-=，从而2)(2k k S S =成立，综上共有3个满足条件的无穷等差数列； 0=n a 或1=n a 或12-=n a n ． 5. （I ）由)0(2)0(f f =，得0)0(=f ,由)21(2)1(f f =及1)1(=f ，得21)1(21)21(==f f 同理，4)21(21)41(1==f f ,归纳得),2,1(21)21( ==i f i i（II ）当12121-≤<i i x 时)21(21)(11---+=i i x k x f)2121)](2121(2121[211111i i i i i i i k a --++=----),2,1(2)41(12 =1-=-i k i 所以{}a n 是首项为)41(21k -，公比为41的等比数列,所以)41(32411)41(21)(lim )(21k ka a a k S n n -=--=+++=∞→ . ∴)(k S 的定义域为≤<k 01，当1=k 时取得最小值21. 6．（1）：当;2,111===S a n 时,24)1(22,2221-=--=-=≥-n n n S S a n n n n 时当故{a n }的通项公式为4,2}{,241==-=d a a n a n n 公差是即的等差数列.设{b n }的通项公式为.41,4,,11=∴==q d b qd b q 则故.42}{,4121111---=⨯-=n nn n n n b b q b b 的通项公式为即 （II ）1142(21)4,4n n n nn a n c n b ---===-12112[13454(21)4],n n n T c c c n -∴=+++=+⨯+⨯++-2314[143454(23)4(21)4]n n n T n n -=⨯+⨯+⨯++-+-,两式相减得].54)56[(91]54)56[(314)12()4444(2131321+-=∴+-=-+++++--=-n n n n n n n T n n T7．（I ）由210S 30－(210+1)S 20+S 10=0得210(S 30－S 20)=S 20－S 10，即210(a 21+a 22+…+a 30)=a 11+a 12+…+a 20, 可得 210·q 10(a 11+a 12+…+a 20)=a 11+a 12+…+a 20. 因为a n >0，所以 210q 10=1, 解得q=12,因而 a n =a 1q n －1=12n ,n=1,2,….(II)因为{a n }是首项a 1=12、公比q=12的等比数列，故 S n =211)211(21--n =1－12n ，nS n =n －n 2n .则数列{nS n }的前n 项和 T n =(1+2+…+n)－(12+222+…+n n2)，T n 2= 12 (1+2+…+n)－(221+322+…+1221++-n n n n ). 前两式相减，得 T n 2= 12 (1+2+…+n)－(12+122+…+n 21)+12+n n =4)1(+n n －211)211(21--n +12+n n ,即 T n =.22212)1(1-+++-n n nn n 8． (1)由S 1=a 1=1,S 2=1+a 2，得3t (1+a 2)－(2t +3)=3t .∴a 2=tt a a t t 332,33212+=+.又3tS n －(2t +3)S n －1=3t ， ①,3tS n －1－(2t +3)S n －2=3t ②,∴①－②得3ta n －(2t +3)a n －1=0. ∴t t a a n n 3321+=-,n =2,3,4…,所以{a n }是一个首项为1公比为tt 332+的等比数列；(2)由f (t )= t t 332+=t 132+,得b n =f (11-n b )=32+b n －1, 可见{b n }是一个首项为1，公差为32的等差数列.于是b n =1+32(n －1)=312+n ;(3)由b n =312+n ,可知{b 2n －1}和{b 2n }是首项分别为1和35，公差均为34的等差数列，于是b 2n =314+n , ∴b 1b 2－b 2b 3+b 3b 4－b 4b 5+…+b 2n －1b 2n －b 2n b 2n +1=b 2(b 1－b 3)+b 4(b 3－b 5)+…+b 2n (b 2n －1－b 2n +1) =－34 (b 2+b 4+…+b 2n )=－34·21n (35+314+n )=－94(2n 2+3n ) 9．（Ⅰ）由y ＝412-x 得2214y x =-，∴2214yx +=,∵x<—2 ，∴214y x +-= ,∴g(x)= 214x +- （x>0）（II ）∵点An(a n ,11+-n a )在曲线y ＝g(x)上(n ∈N +)∴11+-n a = g(a n )= 214n a +- , 并且a n >0 21141n n a a +=∴+ ， ),1(411221N n n a a n n ∈≥=-∴+∴数列{21na}为等差数列. （Ⅲ）∵数列{21na }为等差数列，并且首项为211a =1，公差为4, ∴21na =1+4（n —1） , ∴3412-=n a n ∵a n >0 ，∴341-=n a n ,（Ⅳ）b n ＝1111++n n a a =4341414341--+=++-n n n n ,∴S n ＝b 1＋b 2+…＋b n =43414.......459415--+++-+-n n =4114-+n 10.前(n －1)群中含有1+2+4+…+2n －2=2n －1－1项.因而第n 群的第一个数为a 1+(2n －1－1)d.第n 群含有2n－1项.故这的2n－1项的和为2n －1[a 1+(2n －1－1)d]+ 12×2n －1(2n －1－1)d.11．（1）由⎪⎭⎫ ⎝⎛-=n n S 2114，得)( 221211411N n S S n n n ∈+=⎪⎭⎫ ⎝⎛-=++。

3极限和导数相关知识1.导数的有关概念。

(1)定义：函数y=f(x)的导数f /(x)，就是当0→∆x 时，函数的增量y ∆与自变量的增量x ∆的比xy ∆∆的极限，即xx f x x f x y x f x x ∆-∆+=∆∆=→∆→∆)()(limlim)(00/。

(2)实际背景：瞬时速度，加速度，角速度，电流等。

(3)几何意义：函数y=f(x)在点x 0处的导数的几何意义，就是曲线y=f(x)在点P(x 0,f(x 0))处的切线的斜率。

2． 求导的方法： (1)常用的导数公式：C /=0（C 为常数）； (x m )/=mx m-1(m ∈Q); (sinx)/=cosx; (cosx)/= -sinx ; (e x )/=e x ; (a x )/=a xlnax x 1)(ln /=; e x x a a log 1)(log /=.(2)两个函数的四则运算的导数：).0(;)(;)(2/////////≠-=⎪⎭⎫⎝⎛+=±=±v v uv v u v u uv v u uv v u v u(3)复合函数的导数：x u xu y y ///⋅=3.导数的运用： (1)判断函数的单调性。

当函数y=f(x)在某个区域内可导时，如果f /(x)>0，则f(x)为增函数；如果f /(x)<0，则f(x)为减函数。

(2)极大值和极小值。

设函数f(x)在点x 0附近有定义，如果对x 0附近所有的点，都有f(x)<f(x 0)（或f(x)>f(x 0)）,我们就说f(x 0)是函数f(x)的一个极大值（或极小值）。

(3)函数f(x)在[a,b]上的最大值和最小值的求法。

A 类例题例1求函数的导数)1()3( )sin ()2( cos )1(1)1(2322+=-=+-=x f y x b ax y xx x y ω22222(1)(1)cos (1)[(1)cos ](1):(1)cos x x x x x x y x x''-+--+'=+-解 2222222222222222(1)cos (1)[(1)cos (1)(cos )](1)cos (1)cos (1)[2cos (1)sin ](1)cos (21)cos (1)(1)sin (1)cos x x x x x x x x x x x x x x x x x x x x x x x x x x''-+--+++=+-+---+=+--+-+=+(2)解 y =μ3,μ=ax －b sin 2ωx ,μ=av －by v =x ,y =sin γ γ=ωxy ′=(μ3)′=3μ2·μ′=3μ2(av －by )′=3μ2(av ′－by ′)=3μ2(av ′－by ′γ′)=3(ax －b sin 2ωx )2(a －b ωsin2ωx )(3)解法一 设y =f (μ),μ=v ,v =x 2+1,则y ′x =y ′μμ′v ·v ′x =f ′(μ)·21v －21·2x=f ′(12+x )·21112+x ·2x=),1(122+'+x f x x解法二 y ′=［f (12+x )］′=f ′(12+x )·(12+x )′=f ′(12+x )·21(x 2+1)21-·(x 2+1)′=f ′(12+x )·21(x 2+1) 21-·2x=12+x x f ′(12+x )说明 本题3个小题分别涉及了导数的四则运算法则，复合函数求导的方法，以及抽象函数求导的思想方法 这是导数中比较典型的求导类型解答本题的关键点是要分析函数的结构和特征，挖掘量的隐含条件，将问题转化为基本函数的导数本题难点在求导过程中符号判断不清，复合函数的结构分解为基本函数出差错例2．观察1)(-='n n nxx ，x x cos )(sin ='，x x sin )(cos -='，是否可判断，可导的奇函数的导函数是偶函数，可导的偶函数的导函数是奇函数。

第2讲 二次函数与二次不等式本讲内容包括二次函数与二次方程、二次不等式的关系及高次不等式的解法。

二次方程)0(02≠=++a c bx ax 的解，是相应的二次函数)0(2≠++=a c bx ax y 中，函数值为0时x 的值，即此二次函数的图象在x 轴上的截距（函数图象与x 轴的交点的横坐标）。

二次不等式)0(02>>++a c bx ax 的解，是相应的二次函数)0(2>++=a c bx ax y 中，函数值大于0时x 的值，即此二次函数的图象在x 轴上方时x 的取值范围；同样的，二次不等式)0(02><++a c bx ax 的解，是相应的二次函数)0(2>++=a c bx ax y中，函数值小于0时x 的值，即此二次函数的图象在x 轴下方时x 的取值范围。

因此， 的解)0(02>>++a c bx ax 21x x x x ><或 R x x x ∈≠且0 一切实数的解)0(02><++a c bx ax 21x x x << 无解 无解高次不等式可以先进行因式分解，再运用符号法则将它转化为一次不等式或二次不等式求解。

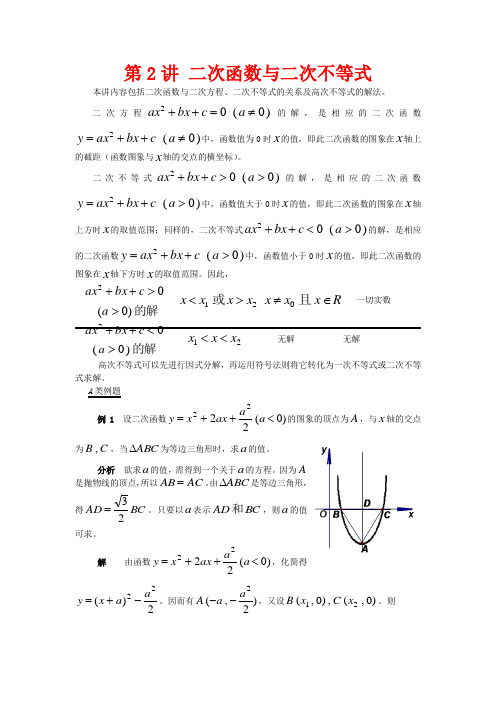
A 类例题例1 设二次函数)0(2222<++=a a ax x y 的图象的顶点为A ，与x 轴的交点为C B ,，当ABC ∆为等边三角形时，求a 的值。

分析 欲求a 的值，需得到一个关于a 的方程。

因为A 是抛物线的顶点，所以AC AB =。

由ABC ∆是等边三角形，得BC AD 23=。

只要以a 表示BC AD 和，则a 的值可求。

解 由函数)0(2222<++=a a ax x y ，化简得2)(22a a x y -+=。

因而有)2,(2a a A --，又设)0,(,)0,(21x C x B 。

则由ABC ∆是等边三角形，得BC AD 23=，即BC y A 23||=。

第1讲 三角函数的定义、图像与性质本专题涉及到任意角的三角函数定义、同角三角函数关系、诱导公式；三角函数的图像及其变换和三角函数的定义域、值域、周期性、单调性、奇偶性等性质，三角函数的定义是三角函数系列知识的源头．A 类例题例１ 角,αβ的终边分别是OA 和OB ，OA 过点(sin ,cos )M θθ-，且02πθ<<，OA和OB 关于直线y x =对称，则角β的集合是( )Ａ．}{2,k k Z ββπθ=-∈ Ｂ． }{2,k k Z ββπθ=+∈ Ｃ．}{,k k Zββπθ=-∈ Ｄ．}{,k k Z ββπθ=+∈(2001年第12届“希望杯”全国数学邀请赛) 分析 根据角的终边所在的象限确定选项． 解 由02πθ<<知(sin ,cos )M θθ-位于第二象限，从而M 点关于直线y x =的对称点在第四象限，即角β是第四象限角．故选(A )．例2 若()sin f x x ⋅是周期为π的奇函数，则()f x 可以是( ) Ａ．sin x Ｂ．cos x Ｃ．sin 2x Ｄ．cos 2x(1999年全国高考卷)分析 采用分析验证和用定义求解的方法．解法一(分析验证) 因为sin x 是奇函数且不恒为零，所以()f x 必须是偶函数，由此排除,A C 项，进而验证知B 选项满足题意．故选(B )．解法二(定义求解) 依题意函数()sin f x x ⋅满足()sin()()sin ()sin()()sin f x x f x xf x x f x x ππ++=⎧⎨--=-⎩，由x 的任意性得 ()()()()f x f x f x f x π-+=⎧⎨-=⎩， 所以()()()[()](2)f x f x f x f x f x ππππ-==-+=--++=+，即函数()f x 是周期为2π的偶函数，只能选B说明 作为选择题解法一直接简明，而解法二揭示了问题的本质，在此基础上可以构造出无数个满足题意的()f x ．例３ 示波器荧屏上有一正弦波，一个最高点在(3,5)B ，与B 相邻的最低点(7,1)C -，则这个正弦波对应的函数是 ．(2003年第14届“希望杯”全国数学邀请赛)分析 设出其解析式，利用正弦函数图像的性质求解．解 设sin()y A x B ωϕ=++，由正弦函数图像的性质可得振幅5(1)32A --==，周期2(73)8T =-=，频率24T ππω==，5122B -==，将(3,5)B 坐标代入，得初相4πϕ=-，故所求表达式为3sin()244y x ππ=-+．说明 在本题中函数的表达式不唯一．情景再现1．方程tan(2)3x π+=[0,2)π上解的个数是( ) .5A .4B .3C .2D２． 当[,]22x ππ∈-，求函数()sin f x x x =的最大值和最小值． ３．函数[]π2,0|,sin |2sin )(∈+=x x x x f 的图象与直线k y =有且仅有两个不同的交点，则k 的取值范围是__________．B 类例题例４ 方程21log sin(5)5x x π=的实根有多少个?分析 仅仅判断根的个数，基本方法是利用函数的图像数形结合求解． 解 原方程实根的个数即为两个函数21log 5y x =和sin(5)y x π=图像的交点的个数． 由于sin 1x ≤，所以只需考虑13232x ≤≤． (1)当1132x ≤<时，由于函数sin(5)y x π=的最小正周期是25，所以在其范围内函数sin(5)y x π=的图像出现两次，在x 轴下方有四个交点;(2)当132x <≤时，其范围的长度是周期的1552倍，由于1x =时sin 50x π=所以有772154⨯=个交点;(3) 1x =时两个函数也有一个交点．综上所述原方程共有41541159++=个实根．说明 利用函数的图像来确定某些特殊的非常规方程的实根个数是一条十分重要的途径．在“数形结合”时，特别强调“以数定形”，如方程sin x x =的解只有一个（当(0,)2x π∈时，sin x x <）．例５ 在平面直角坐标系xOy 中，函数()sin cos (0)f x a ax ax a =+>在一个最小正周期长的区间上的图像与函数()g x =的图像所围成的封闭图形的面积是 ．(2004年全国高中数学联赛) 分析 利用正弦函数图像的对称性补形转化求解． 解1()),arctanf x ax aϕϕ=+=，它的最小正周期为2a π，．由()f x 的图像与()g x 的图像围成的封闭形的对称性，可将该图形割补成长为2aπ，宽为． 例６ 若5,123x ππ⎡⎤∈--⎢⎥⎣⎦，则2t a n ()t a n ()c o s ()366y x x x πππ=+-+++的最大值是 ．(2003年全国数学联赛) 分析 化弦后利用单调性求解． 解22tan()cot()cos()336y x x x πππ=+++++2cos()6sin(2)3x x ππ=-+++，由于函数的每一部分在给定区间上都是增函数，所以当3x π=-． 例７ 已知函数()sin()(0,0)f x x ωϕωϕπ=+>≤≤是R 上的偶函数，其图像关于点3(,0)4π对称，且在区间[0,]2π是单调函数，求ω和ϕ的值．分析 运用三角函数对称的特征求解，也可用偶函数和关于点对称的定义求解．解法一 由偶函数关于x 轴对称，知当0x =时函数()f x 取最大值或最小值，所以sin 1,ϕ=±又0ϕπ≤≤所以2πϕ=;另一方面函数()f x 的图像关于点3(,0)4π对称，此点是函数图像与x 轴的一个交点，所以当34x π=，3sin()042ππω+=，即33cos 0,,442k πππωωπ==+，2(21)3k ω=+，0,1,2,k =．当0k =时，22,()sin()332f x x πω==+在[0,]2π上是减函数;当1k =时，2,()sin(2)2f x x πω==+在[0,]2π上是减函数;当2k ≥时，10()sin()3f x x ωωϕ≥=+在[0,]2π上不是减函数．综上所述23ω=或2,2πωϕ==． 解法二 由()f x 是偶函数，得()()f x f x -=即sin()sin()x x ωϕωϕ-+=+，所以cos sin cos sin x x ϕωϕω-=对任意x 都成立，只能是cos 0ϕ=，又0ϕπ≤≤，所以2πϕ=．由()f x 的图像关于点3(,0)4π对称，得33()()44f x f x ππ-=-+，令0x =得3()04f π=，以下同解法一． 例８．已知,[,],44x y a ππ∈-∈R ，且 33sin 204sin cos 0x x a y y y a ⎧+-=⎨++=⎩，则cos(2)x y += ． 分析 构造函数用单调性求解，或利用函数的奇偶性和函数图像特征求解． 解法一 由已知得33sin 2(2)sin(2)x x a y y +==-+-，现构造函数3()sin f t t t =+，由此得()(2)f x f y =-，而函数()f t 在[,]44ππ-上是增函数，所以有2,20x y x y =-+=，即cos(2)x y +=1． 解法二记3()sin 2f x x x a =+-，3(2)(2)sin(2)2g y y y a =++，于是3()sin 2g x x x a =++，又(),()y f x y g x ==分别是R 上的增函数，所以它们的图像与x 轴只有一个交点，而3()sin 2g x x x a =++3[()sin()2]x x a =--+--()f x =--，即()()f x g x -=-，所以函数()y f x =与()y g x =的图像关于原点对称，那么它们的交点也关于原点对称． 记()0,()0f x g x ==的根分别是,2x y ，则1(2)02x y +=， 所以cos(2)x y +=1．情景再现４．函数42cos sin y x x =+的最小正周期是 ．５．已知x ∈R ，则函数sin cos ()max sin ,cos ,2x x f x x x +⎧⎫=⎨⎬⎩⎭的最大值与最小值的和是 ．６．若函数s i n (0)y x ωω=>在区间[0,1]上至少出现50次最大值，则ω的最小值是 ．C 类例题例９． 两个周期函数12,y y 的最小正周期分别为,a b ，且b na =，其中2,n n N ≥∈．如果函数12y y y =+的最小正周期为t ，那么下列5种情形：①t a <， ②t a =， ③t b =， ④t b >， ⑤a t b <<．可能出现的情形是 ．（填写序号）分析 周期是三角函数的重要性质，构造三角函数回答．解 由题意知b 是12y y y =+的周期，所以t b ≤，情形④不可能出现；由21y y y =-知如果t a =，那么a 也是2y 的最小正周期，矛盾，所以情形②不可能出现；其它三种情形都有可能出现．下面的例子说明其它三种情形是可能的：取22sin sin3xy x =+，则其最小正周期是6b π=．令12s i n 3xy =-，此时3,2,a t t a ππ==<；令1s i n y x =-，此时2,3,a t a t b ππ==<<；令1sin y x =，此时2,6,a t t b ππ===．所以可能出现的情形是①③⑤例1０． 函数22()cos 2sin cos sin F x x x x x Ax B =+-++，当3[0,]2x π∈时的最大值M 与参数,A B 有关，问,A B 取什么值时M 为最小?证明你的结论(1983年全国数学联赛)分析 在M 是最大值的前提下通过特殊值构造不等关系， 并结合函数图像直观分析． 解法一(数形结合分析)（1）若0A B ==，|)42sin(2|)(π+=x x F 则当89,85,8πππ=x 时，)(x F 的最大值M 为2．（2）若0,0A B =≠，|)42sin(2|)(B x x F ++=π，此时M=2|}2||,2max{|>-+B B（3）若0,0A B ≠=，|)42sin(2|)(Ax x x F ++=π，若0A >时，|82|)8(ππ⋅+=A F >2，此时2>M ；若0A <时，2|852|)85(>⋅+-=ππA F ，此时也有2>M ．（4）若0,0A B ≠≠如图，直线B Ax y +=必有一部分在第一或第四象限，与射线321,,l l l 中至少一条相交，交点处两函数B Ax y +=与)42sin(2π+=x y 函数值同号，其和的绝对值必小于2，因此也有2>M ．说明 问题的关键就是考察三个函数值59(),(),()888F F F πππ的值，从而得：解法二 由⎪⎪⎪⎩⎪⎪⎪⎨⎧++=++-=++=|892|)89( |852|)85( |82|)8(B A F B A F B A F ππππππ，将这三个函数值综合起来考虑． 当0A =时同上，当A ≠0时讨论如下：（1）若B A +85π<0，则2)85(>πF ； （2）若B A +85π≥0，A B A B A 84)85(89πππ++=+与A B A B A 84)85(8πππ-+=+至少有一个大于0，即2)89(>πF 或2)8(>πF 至少有一个成立，因此总有2>M ．从而当且仅当0A B ==时，2=M ，其他情况下均有2>M ．情景再现７．已知当]1,0[∈x 时，不等式0sin )1()1(cos 22>-+--θθx x x x 恒成立，试求θ的取值范围．（1999年全国高中数学联赛题）习题１． 若角α是第四象限的角，则πα-是( )Ａ．第一象限 Ｂ．第二象限 Ｃ．第三象限 Ｄ．第四象限 ２．关于函数()4sin(2)3f x x π=+()x R ∈，有下列命题：①()y f x =是以2π为最小正周期的函数；②()y f x =的表达式可以改写为4cos(2)6y x π=-；③()y f x =的图像关于点(,0)6π-对称；④()y f x =的图像关于直线6x π=-对称．其中正确的命题的序号是_____．（注：把你认为正确的命题的序号都填上．）３．若,A B 是锐角ABC ∆的两个内角，则点(cos sin ,sin cos )P B A B A --在第 象限．４．设()f x 是定义域为R ，最小正周期为32π的函数，若 cos ,(0)()2sin ,(0)x x f x x x ππ⎧-≤<⎪=⎨⎪≤<⎩，则15()4f π-的值是 ． ５．设关于x 的方程222sin (2cos3)0x x θθ--+=，其中[0,]2πθ∈，则该方程实根的最大值是 ，实根的最小值是 ．６．关于θ角的函数cos 22cos 43y a a θθ=-+-，当[0,]2πθ∈时恒大于0，则实数a 的取值范围是 ．７．已知函数()sin()(0,)f x x x R ωϕω=+>∈满足()(1)(2)f x f x f x =+-+．若sin(9),sin(9)A x B x ωϕωωϕω=++=+-，则A 与B 的大小关系是 ．８．已知函数sin 2cos 2y x a x =+，在下列条件中分别求实数a 的值． (1)函数图像关于原点对称; (2)函数图像关于直线8x π=-对称．９．设,αβ分别是方程cos(sin )x x =和sin(cos )x x =在区间(0,)2π上的解，确定,αβ的大小关系．１０．三个数a,b,c ∈)2,0(π，且满足a a =cos ，b b =cos sin ，c c =sin cos ，按从小到大的顺序排列这三个数．（16届全苏竞赛题）１１．已知集合M 是满足下列性质的函数()f x 的全体;存在非零常数T ，对任意x R ∈，有()()f x T Tf x +=成立．若函数()sin f x kx M =∈,求实数k 的取值范围．１２．已知：定义在R 上的函数)(x f 为奇函数，且在),0[+∞上是增函数．若不等式0)sin 2()32(cos >-+-θθm f f 对任意R ∈θ恒成立．求实数m 的取值范围．本节“情景再现”解答：1．解 本题实质是函数周期性的应用．函数tan(2)3y x π=+的最小正周期2T π=，而区间长度是2π，是周期的4倍，而正切函数在每个周期内是单调的，故解的个数为4．选B ． ２．解 化成一个角的一个三角函数形式，用函数的单调性求解．()2sin()3f x x π=+，[,]22x ππ∈-，由5[,]366x πππ+∈-及正弦函数的单调性知其最大值为2，最小值为1-．３．解3sin ,[0,]()sin ,(,2]x x f x x x πππ∈⎧=⎨-∈⎩，作出其图像，可知有两个交点时的k 的范围为31<<k ．４．解42cos sin y x x =+222cos (1sin )sin x x x =-+2221711sin cos 1sin 2cos 4488x x x x =-=-=+．所以函数42cos sin y x x =+的最小正周期为2π． ５．解 注意到sin cos ()max sin ,cos ,2x x f x x x +⎧⎫=⎨⎬⎩⎭max sin ,cos ,sin()4x x x π⎧⎫=+⎨⎬⎩⎭，显然()f x 的最大值为1，可以通过作出sin y x =和cos y x =的图像得到{}max sin ,cos x x 的最小值是2-，在524x k ππ=+时取得，而此时sin()4x π+的值为1-，所以()f x 的最小值是2-，从而最大值与最小值的和是12-． ６．解 函数在一个周期内只能取得一个最大值，其图像从原点开始并注意到可在端点1处取到最大值，所以在区间[0,1]内至少有49周期再加14个周期，由21(49)14πω+=得1972πω=，即ω的最小值是1972π．７．解设θθsin )1()1(cos )(22x x x x x f -+--=， 则由]1,0[∈x 时0)(>x f 恒成立，有0sin )0(>=θf ，0cos )1(>=θf ，22()([(12(1f x x x x ∴=+---2(1(1)x x x x +--0)cos sin 21)(1(2]sin )1(cos [2>-----=θθθθx x x x ，当θθθcos sin sin +=x 时，0sin )1(cos =--θθx x ，令θθθcos sin sin 0+=x ，则100<<x ，0)21cos sin )(1(2)(000>--=θθx x x f ，故212sin 21>θ，即212sin >θ，且0cos ,0sin >>θθ，所求范围是：Z k k k ∈+<<+,1252122ππθππ反之，当Z k k k ∈+<<+,1252122ππθππ时，有212sin >θ，且0cos ,0sin >>θθ，于是只要]1,0[∈x ，必有0)(>x f 恒成立．“习题”解答：１．解 利用诱导公式推导的方法确定选项．角α和角α-的终边关于x 轴对称，所以角α-的终边在第一象限，又角α-和角πα-的终边关于原点对称，所以角πα-的终边在第三象限． 故选(C )．２．解 作出函数()y f x =的图像，由其直观性可知正确命题的序号是②③３．解 由正弦函数的单调性和诱导公式求解．因为ABC ∆是锐角三角形，所以090A B +>，即090,90A B B A >->-，所以sin cos A B >，sin cos B A >，点P 应在第二象限．４．解 由周期性和诱导公式求解．15()4f π-1593()()424f f πππ=-+=3sin 42π==． ５．解 数形结合求解．设两实根分别为,αβ，则22sin 2cos αβθαβθ+=⎧⎨=-⎩，于是222()210αβαβαβ+=+-=，又由[0,]2πθ∈知02αβ≤+≤．于是满足条件2210αβ+=且02αβ≤+≤)在如图所示的弧AB 或CD 上．由此可知实根的最大值为3D B x y ==是A C x y ==６．解 可以转化为二次函数求最小值，由最小值大于0求出a 的范围．现用分离变量的方法求解．由cos 22cos 430,[0,]2a a πθθθ-+->∈，得22cos 2cos a θθ->-，而22cos 2[(2cos )]42cos 2cos θθθθ-=--++--，由基本不等式得其最大值是4-4a >-７．解 发现函数()f x 的周期性，运用周期变换求解． 由()(1)(2)f x f x f x =+-+得(1)(2)(3)f x f x f x +=+-+，两式相加得(3)()f x f x +=-，即得(6)()f x f x +=，从而可知()f x 是以6为周期的函数，所以(9)A f x =+(3)(3)f x f x =+=-(9)f x B =-=，即A 与B 的大小关系是A B =．８．解 sin 2cos2)y x a x x ϕ=+=+，其中tan a ϕ=， (1)关于原点对称则有sin 0,k ϕϕπ==，所以tan 0a ϕ==; (2)关于直线8x π=-对称则有sin()14πϕ-+=±，即34k πϕπ=+，所以tan 1a ϕ==-． ９．解 构造函数，运用其单调性求解． 记()cos(sin ),02f x x x x π=-≤≤，因为(0)101f =-=，()cos1022f ππ=-<，所以()0f x =在(0,)2π上有根，又()f x 在(0,)2π上单调递减，所以()0f x =在(0,)2π上的根α是唯一的．同样记()sin(cos )g x x x =-，由(0)0,()02g g π><及()g x 在(0,)2π上单调递减，所以()0g x =在(0,)2π上的根β存在且是唯一的．由cos(sin )αα=两边取sin 得 sin[cos(sin )]sin αα=由于sin(cos )x x =的解是唯一的，所以sin αβ=，故sin βαα=<．１０．解 运用单调性结合分类讨论求解．（1）若b a =，则a a c os sin c os =，但由a cos )2,0(π∈，故有a a cos sin cos >矛盾，即a≠b ．（2）若b a <，则由单调性可知b a cos cos >，又由b a <及题意可得b a cos sin cos <，而b b cos cos sin <，因此又可得b a cos cos <，从而产生矛盾．因此b a >．类似地，若a c =，则由题意可得a a sin cos cos =，从而可得a a sin =与a a sin >矛盾；若a c <，则a a c <<sin sin ，即a c <sin ，a c cos sin cos >∴，即a c >矛盾．综上可得：c a b <<．１１．解 运用等式恒成立的条件求解．当0k =时，()0f x =显然()f x M ∈；当0k ≠时，因为()sin f x kx M =∈所以存在非零常数,T对x R ∈任意，有成立，即sin()sin kx kT T kx +=对x R ∈恒成立．即sin cos cos sin sin kx kT kx kT T kx +=，sin (cos )cos sin 0kx kT T kx kT -+=恒成立，由等式恒成立知只能有cos 0kT T -=，且sin 0kT =，从而1T =±，进而求得()k m m Z π=∈．本题也可用特殊值求解．１２．解 先证明函数在R 上是增函数，运用单调性去掉()f x 后转化为不等式恒成立求解． 设)0,(,21-∞∈x x ，且21x x <，则),0(,21+∞∈--x x ，且21x x ->-．∵)(x f 在),0[+∞上是增函数，∴)()(21x f x f ->-又)(x f 为奇函数∴)()(21x f x f <．∴)(x f 在)0,(-∞上也是增函数．即函数)(x f 在)0,(-∞和),0[+∞上是增函数，且)(x f 在R 上是奇函数，所以)(x f 在),(+∞-∞上是增函数．∵0)sin 2()32(cos >-+-θθm f f ，∴)sin 2()32(cos θθ-->-m f f ，)2(sin )32(cos m f f ->-θθ， m 2sin 32cos ->-θθ，2sin sin 222++>θθm ，161541sin 2+⎪⎭⎫ ⎝⎛+>θm 。

第 17 讲 同 余同余是数论中的重要概念，同余理论是研究整数问题的重要工具之一。

设m 是一个给定的正整数，如果两个整数a 与b 用m 除所得的余数相同，则称a 与b 对模同余，记作)(mod m b a ≡，否则，就说a 与b 对模m 不 同余，记作)(mod m b a ≡，显然，)(|)(,)(mod b a m Z k b km a m b a -⇔∈+=⇔≡； 1、 同余是一种等价关系，即有自反性、对称性、传递性1).反身性：)(mod m a a ≡；2).对称性：)(mod )(mod m a b m b a ≡⇔≡；3). 传递性：若)(mod m b a ≡，)(mod m c b ≡则)(mod m c a ≡; 2、加、减、乘、乘方运算若 a b ≡（mod m ） c d ≡（mod m ）则 a c b d ±≡±（mod m ），ac bd ≡（mod m ），nna b ≡（mod m ） 3、除法设 ac bd ≡（mod m ）则 a b ≡（mod(,)mc m ）。

A 类例题例1．证明： 一个数的各位数字的和被9除的余数等于这个数被9除的余数。

分析 20≡2(mod9)，500≡5(mod9)，7000≡7(mod9)，……，由于10n －1=9M ，则10n≡1(mod9)，故a n ×10n≡a n (mod9)。

可以考虑把此数变为多项式表示a n ×10n+ a n-1×10n-1+…+ a 1×10+a 0后处理。

证明 设a=110n n a a a a -=a n ×10n + a n-1×10n-1+…+ a 1×10+a 0，∵10≡1(mod9)，∴10n ≡1(mod9)，∴a n ×10n+ a n-1×10n-1+…+ a 1×10+a 0≡a n + a n-1+…+ a 1+a 0。

第1讲 二次函数的图象和性质本讲内容包括二次函数的图象和性质，二次函数在给定区间上的最值。

二次函数)0(2≠++=a c bx ax y 是具有典型意义的初等函数，它的图象是以垂直于x 轴的直线abx2-=为对称轴的抛物线。

其中，二次项系数a 决定了抛物线的形状（a 的符号和|a |的大小分别确定抛物线的开口方向和开口大小）；常数c 是抛物线在y 轴上的截距（抛物线与y 轴的交点的纵坐标）；一次项系数b 与图象的左右平移有关。

二次函数)0(2≠++=a c bx ax y 中，当0>a 时，若abx 2-≤，即]2,(a b x -∞-∈，则函数值y 随着自变量x 的增加而减少；若ab x 2-≥，即),2[∞+-∈a b x ，则函数值y 随着自变量x 的增加而增加；当0<a 时，若ab x 2-≤，即]2,(a b x -∞-∈，则函数值y 随着自变量x 的增加而增加；若abx 2-≥，即),2[∞+-∈a b x ，则函数值y 随着自变量x 的增加而减少。

当a b x 2-=时，二次函数取最小值a 4∆-（0>a ）或最大值a4∆-（0<a ）。

其中，.42ac b -=∆ 为叙述方便，我们用符号)(x f 表示x 的函数。

)(a f 表示a x =时，函数)(x f 的值。

如452)(2+-=x x x f ，则.743532)3(2=+⨯-⨯=fA 类例题例1如图，直线1=x 是二次函数cbx ax y ++=2的图象的对称轴，则 （ ）分析 由于所给的条件是二次函数的图象即函数的“形”的特征，欲求的结论是关于系数的不等式即函数的“数”的性质。

因此，解题的关键在于确定结论中系数及其表达式的几何意义，进而通过图象进行判断。

解1 设c bx ax x f ++=2)(.，则c b a f c b a f +-=-++=)1(,)1(。

由图象可知，0)1(,0)1(>-<f f ，故可以排除A 、B 。

2012江苏省数学竞赛《提优教程》教案：第76讲平几问题选讲第16讲 平几问题选讲平面几何在高中竞赛和国际竞赛中占有重要的地位，本讲将对平几中的一些典型问题的选讲，强化解平几问题的典型思想方法.A 类例题例 1 如图，已知正方形ABCD ，点E 、F 分别在BC 、CD 上，且BE +DF =EF ，试求∠EAF 的度数.（1989年全国冬令营）分析 注意到BE +DF =EF ，很容易想到“截长补短”的方法．解 延长CB 到F'，使得BF'= DF ，连结AF'显然∆AF'B ≌∆AFD ．∴∠BAF'=∠DAF ，AF'=AF ．又∵EF'=BE +BF'=BE +DF ，AE 为公共边， ∴∆AF'E ≌∆AFE ． ∴∠EAF'=∠EAF ． 又∵∠FAF'=∠BAD =90º，FD CAFD CA∴∠EAF=45º．说明本题∆AF'B可以看作是∆AFD顺时针旋转90º得到的；本题也可以延长CD或旋转∆ABE.例2 如图，A 、B 、C 、D 为直线上四点，且AB =CD ，点P 为一动点，若∠APB =∠CPD ，试求点P 的轨迹．（1989年全国初中数学联赛）分析 由于已知的两个条件AB =CD 和∠APB =∠CPD ，分散在两个三角形中，需要把它们集中，于是可以进行平移或添加辅助圆建立这两个已知条件间的联系.证法一 分别过点A 、B 作PC 、PD 的平行线得交点Q .连结PQ . 在△QAB 和△PCD中,显然 ∠QAB ＝∠PCD ,∠QBA ＝∠DABCPDC.由AB=CD,可知△QAB≌△PCD.有QA＝PC，QB＝PD，∠AQB＝∠CPD.于是,PQ∥AB，∠APB＝∠AQB.则A、B、P、Q四点共圆，且四边形ABPQ 为等腰梯形.故AP＝BQ.所以PA＝PD.即点P的轨迹是线段AD的垂直平分线.证法二作△PBC的Array外接圆交PA、PD分别为E、F，连结BE、CF，∵∠APB=∠CPD，∴BE=CF，∠ABE=∠EPC=∠BPF =∠DCF. 又∵AB=CD，∴△ABE≌△DCF.∴∠PAB＝∠PDC.∴PA＝PD.即点P的轨迹是线段AD的垂直平分线.说明同样地，也可以作△PAD的外接圆，目的是建立条件AB=CD和∠APB=∠CPD之间的联系.证法三 由三角形的面积公式易得PA ·PB =PC ·PD ，PA ·PC =PB ·PD ，两式相乘，化简得PA ＝PD .即点P 的轨迹是线段AD 的垂直平分线. 证法四 由正弦定理得PAsin ∠PBA =AB sin ∠APB ,PD sin ∠PCD =CD sin ∠CPD, 从而PA sin ∠PBA =PD sin ∠PCD ，同理可得PAsin ∠PCB =PD sin ∠PBD，而sin ∠PBA =sin ∠PBD ，sin ∠PCD =sin ∠PCB ，化简得PA ＝PD . 即点P 的轨迹是线段AD 的垂直平分线.例3．AD 是△ABC 的高线，K 为AD 上一点，BK交AC 于E ，CK 交AB 于F .求证：∠FDA ＝∠EDA .分析 为了把已知条件之间建立联系，可以通过作平行线的方法.证明 如图，过点A 作BC 的平行线,分别交直线DE 、DF 、BE 、CF 于Q 、P 、N 、M .显然，AN BD ＝KA KD ＝AMDC. 有BD ·AM ＝DC ·AN .(1)由BD AP ＝FB AF ＝BCAM ，有 AP ＝BCAMBD ·.(2)由DC AQ ＝EC AE ＝BCAN ，有 AQ ＝BCANDC ·.(3)对比(1)、(2)、(3)有 AP ＝AQ .显然AD 为PQ 的中垂线，故AD 平分∠PDQ . 所以，∠FDA ＝∠EDA .说明 这里,原题并未涉及线段比,添加BC 的平行线,就有大量的比例式产生,恰当地运用这些比例式,就使AP 与AQ 的相等关系显现出来.本题证明方法很多，例如可以过点E 、F 作BC 的垂线，也转化为线段的比来研究.情景再现1．点E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF ，CE ，设AF ，CE 交于点G ， 则ABCDAGCD S S 矩形四边形 等于（ ）A ．56B ．45C ．34D ．23 （2002年全国初中数学竞赛试题）ABC DE FG2. 在△ABC 中，D 为AB 的中点，分别延长CA ，CB到点E ，F ，使DE =DF ；过E ，F 分别作CA ，CB 的垂线，相交于P ．设线段PA ，PB 的中点分别为M ，N ．求证：∠PAE =∠PBF ． (2003年全国初中数学竞赛)3．如图，四边形ABCD 为平行四边形，∠BAF ＝∠BCE .求证：∠EBA ＝∠ADE . B 类例题例4 如图，AD 为△ABC 的中线，E 、F 分别在AB 、AC 上，且DE DF ，求证：BE +CF >EF .E DGA B F CCE分析 由要证的结论，可联想到构造三角形，运用两边之和大于第三边解决问题.要构造三角形，就要移动一些线段，从而可以运用平移、旋转、作对称等方法，于是有如下证法. 证法一 延长FD 到F'，使得DF'=DF ，连结BF'、EF'，由D 为BC 的中点，显然△DBF'≌△DCF .于是BF'=CF ，又因为DE 垂直平分FF'，所以EF =EF'.在三角形BEF'中，BE +BF'>EF'.从而BE +CF >EF .证法二 作点B 关于DE 的对称点B'，连结EB'、DB'、FB'.则EB'=BE ，不难得到DB'=DB =DC ，∠B'DF ＝∠CDF .从而可知B 、C 关于DF 对称，于是B'F =CF ，在三角形B'EF 中，B'E +B'F >EF .从而BE +CF >EF .说明证法一也可以从中心对称角度来理解，F'和F 关于点D 对称.BCCB例5 如图，△ABC中，O为外心，三条高AD、BE、CF交于点H，直线DE和AB交于点M，DF和AC交于点N．求证：（1）OB⊥DF，OC⊥DE．（2）OH ⊥MN ． （2001年全国高中数学联赛）证法一 （1）显然B ，D ，H ，F 四点共圆，H ，E ，A ，F 四点共圆， ∴∠BDF =∠BHF =180°-∠EHF =∠BAC ．∠OBC =12 (180°-∠BOC )=90°-∠BAC . ∴OB ⊥DF ． 同理OC ⊥DE ．（2）∵CF ⊥MA ，∴MC 2-MH 2=AC 2-AH 2……①∵BE ⊥NA ，∴NB 2-NH 2=AB 2-AH 2……② ∵DA ⊥BC ，∴DB 2-CD 2=BA 2-AC 2……③ ∵OB ⊥DF ，∴BN 2-BD 2=ON 2-OD 2……④ ∵OC ⊥DE ，∴CM 2-CD 2=OM 2-OD 2……⑤ ①-②+③+④-⑤，得O ABC H FE DNMNH2-MH2=ON2-OM2OM2-MH2=ON2-NH2所以OH⊥MN．证法二以BC所在直线为x轴，D为原点建立直角坐标系，设A(0，a)，B(b，0)，C(c，0)，则∴直线AC的方程为，直线BE的方程为由得E点坐标为E() 同理可得F()直线AC的垂直平分线方程为直线BC的垂直平分线方程为由得O()∵∴OB⊥D F同理可证OC⊥DE．在直线BE的方程中令x＝0得H(0，) ∴直线DF 的方程为由得N ()同理可得M ()∴∵k OH ·k MN ＝－1，∴OH ⊥MN ．链接 本题证法一中用到了定理：设P 、Q 、A 、B 为任意四点，则PA 2-PB 2=QA 2-QB 2 PQ ⊥AB ．对于这个定理可参见本书高一分册地十八讲《平几中的几个重要定理（一）》.证法二用的解析法.例 6 锐角△ABC 中，AB >AC ,O 点是它的外心,射点.线AO 交BC 边于D已知：cos B +cos C =1，求证：△ABD 与△ACD 的周长相等. 证明 作OE ⊥AC 、OF ⊥AB ，E 、F 是垂足.O ABC DFE由三角形外心性质知：∠AOE =∠B ，∠AOF =∠C .记BC =a 、CA =b 、AB =c .于是OAEOAFAC AB CAD AD AC BAD AD AB S S DC BD ACDABC∠∠⋅=∠⋅⋅∠⋅⋅==∆∆sin sin sin sin 2121CBb c B C b c AOE AOF AC AB cos 1cos 1cos cos cos cos --⋅=⋅=∠∠⋅=由余弦定理得ba c ac b b a c a c b DC BD -++-=----=2222)()(；从而BD =)(21c b a -+. 此时，AB +BD =)(21c b a ++=AC +CD .得证. 说明 本题用到了正余弦定理，以及三角形面积公式，同时运用了代数的方法证了几何题. 情景再现4．△ABC 中，∠B =2∠C ，求证：2AB >AC ．(2002年江苏省数学夏令营试题）5．已知同一平面的两个三角形A 1B 1C 1，A 2B 2C 2，并且A 1到B 2C 2的垂线，B 1到C 2A 2的垂线，C 1到A 2B 2的垂线交于同B B 11一点P .求证：A 2到B 1C 1的垂线，B 2到C 1A 1的垂线，C 2到A 1B 1的垂线也交于同一点.6.在△ABC 中,AD 是BC 边上的中线,点M 在AB 边上,点N 在AC 边上,并且∠MDN ＝90°.如果BM 2＋CN 2＝DM 2＋DN 2,求证：AD 2＝41(AB 2＋AC 2). C 类例题例7．如图，⊙O 是△ABC 的边BC 外的旁切圆,D 、E 、F 分别为⊙O 与BC 、CA 、AB 的切点.若OD与EF 相交于K ,求证：AK 平分BC . 证明 如图，过点K 作BC 的行平线分别交直线AB 、AC 于Q 、P 两点,连OP 、OQ 、OE 、OF .由OD ⊥BC ，可知OK ⊥PQ .O由OF⊥AB，可知O、K、F、Q四点共圆，有∠FOQ＝∠FKQ.由OE⊥AC，可知O、K、P、E四点共圆.有∠EOP＝∠EKP.显然，∠FKQ＝∠EKP，可知∠FOQ＝∠EOP.由OF＝OE，可知Rt△OFQ≌Rt△OEP.则OQ＝OP.于是，OK为PQ的中垂线，故QK＝KP.所以，AK平分BC.例8 如果三角形三边的平方成等差数列，那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.证明 将△ABC 简记为△，由三中线AD ，BE ，CF 围成的三角形简记为△′.G 为重心，连DE 并延长到H ，使EH =DE ，连HC ，HF ，则△′就是△HCF .(1)a 2，b 2，c 2成等差数列△∽△′.若△ABC 为正三角H形，易证△∽△′.不妨设a ≥b ≥c ，有 CF =2222221c b a -+， BE =2222221b ac -+， AD =2222221a cb -+.将a 2+c 2=2b 2，分别代入以上三式，得CF =a 23，BE =b 23，AD =c 23. ∴CF :BE :AD =a 23:b 23:c 23=a :b :c . 故有△∽△′.(2)△∽△′⇒a 2，b 2，c 2成等差数列. 当△中a ≥b ≥c 时， △′中CF ≥BE ≥AD . ∵△∽△′，∴∆∆S S '＝(aCF )2. 据“三角形的三条中线围成的新三角形面积等于原三角形面积的43”，有∆∆S S '=43. ∴22a CF =43⇒3a 2=4CF 2=2a 2+b 2-c2⇒a 2+c 2=2b 2.例9 四边形ABCD 内接于圆，△BCD ，△ACD ，△ABD ，△ABC 的内心依次记为I A ，I B ，I C ，I D .试证：I A I B I C I D 是矩形.(第一届数学奥林匹克国家集训选拔试题)证明 连接AI C ，AI D ，BI C ，BI D 和DI B .易得∠AI C B =90°+21∠ADB =90°+21∠ACB =∠AI D B ⇒A ，B ，I D ，I C 四点 共圆.同理，A ，D ，I B ，I C 四点共圆.此时 ∠AI C I D =180°-∠ABI D =180°-21∠ABC ， ∠AI C I B =180°-∠ADI B =180°-21∠ADC ， ∴∠AI C I D +∠AI C I B=360°-21(∠ABC +∠ADC ) =360°-21×180°=270°. 故∠I B I C I D =90°.同样可证I A I B I C I D 其它三个内角皆为90°.该四边形必为矩形.A B CDI CI DAI I B说明 本题的其他证明可参见《中等数学》1992；4例10 设D 是ABC∆的边BC 上的一点，点P 在线段AD 上，过点D 作一直线分别与线段AB 、PB 交于点M 、E ，与线段AC 、PC 的延长线交于点F 、N .如果DE=DF ，求证：DM=DN.(首届中国东南地区数学奥林匹克) 证明 对AMD∆和直线BEP 用梅涅劳斯定理得：1(1)AP DE MBPD EM BA⋅⋅=，对AFD∆和直线NCP 用梅涅劳斯定理得：1(2)AC FN DPCF ND PA⋅⋅=，对AMF∆和直线BDC 用梅涅劳斯定理得：1(3)AB MD FCBM DF CA⋅⋅=（1）（2）（3）式相乘得：1DE FN MDEM ND DF ⋅⋅=，又DE=DF ， 所以有DM DN DM DE DN DE=--， 所以DM=DN.说明 本题是直线形，当然可以用解析法，请同学们试一试.情景再现7．设点D 为等腰ABC ∆的底边BC 上一点，F 为过A 、D 、C 三点的圆在ABC ∆内的弧上一点，过B 、D 、F 三点的圆与边AB交于点E .求证：CD EF DF AE BD AF⋅+⋅=⋅.(首届中国东南地区数学奥林匹克)8. 如图，O 、H 分别是锐角△ABC 的外心和垂心，D 是BC 边的中点，由H向∠A 及其外角平分线作垂线，垂足分别是E 是F .证明：D 、E 、F 三点共线.（2004年全国高中数学联赛四川省初赛）习题161．正方形ABCD 的中心为O ，面积为1989㎝2.P 为正方形内一点，且∠OPB =45°，PA :PB =5:14.则PB =__________.(1989年全国初中联赛)2.如图,在△ABC 中,AB ＝AC ,D是底边BC 上一点,E 是线段AD 上一点且∠BED ＝2∠CED ＝∠A .求证：BD ＝2CD .3.如图，等腰三角形ABC 中，P 为底边BC 上任意点，过P 作两腰的平行线ABDEPB CPOA BCD分别与AB ，AC 相交于Q ，R 两点，又P '的对称点，证明：P '在△ABC 的外接圆上.(2002年全国初中数学联合竞赛试卷)4.设点M 在正三角形三条高线上的射影分别是M 1，M 2，M 3(互不重合).求证：△M 1M 2M 3也是正三角形.5.在△ABC 中,BD 、CE 为角平分线,P 为ED 上任意一点.过P 分别作AC 、AB 、BC 的垂线,M 、N 、Q 为垂足.求证：PM ＋PN ＝PQ .6.在Rt △ABC 中，AD 为斜边BC 上的高，P 是AB 上的点，过A 点作PC 的垂线交过B 所作AB 的垂线于Q 点.求证：PD 丄QD .7.设M 1、M 2是△ABC 的BC 边上的点,且BM 1＝CM 2.任作一直线分别交AB 、AC 、AM 1、AM 2于P 、Q 、N 1、N 2.试证：APAB ＋AQ AC＝11AN AM ＋22ANAM .8.AD ，BE ，CF 是锐角△ABC 的三条高.从A 引EF 的垂线l 1，从B 引FD 的垂线l 2，从C 引DE 的垂线l 3.求证：l 1，l 2，l 3三线共点.9. AD 是Rt △ABC 斜边BC 上的高,∠B 的平分线交AD 于M ,交AC 于N .求证：AB 2－AN 2＝BM ·BN . 10．已知等腰△ABC中，∠BAC =100°，延长线段AB 到D ，使得AD =BC ，连结CD ，试求∠BCD 的度数.11.圆外一点P 作圆的两条切线和一条割线，切点为A ，B . 所作割线交圆于C ，D 两点，C 在P ，D 之间.在弦CD 上取一点Q ，使.DAQ PBC ∠=∠求证：.DBQ PAC ∠=∠12.已知两个半径不相等的圆O 1与圆O 2相交于M 、N 两点，且圆O 1、圆O 2分别与圆O 内切于S 、T 两点.求证：OM ⊥MN 的充分必要条件是S 、N 、T 三点共线. （1997年全国高中数学联赛）BDCA本节“情景再现”解答： 1．解一：连结AC ，从而可得G 为△ABC 的重心，于是CG =2GE ，AEC AGCS S ∆∆=∴32．显然ABCD 4121矩形S S SABC AEC==∆∆．ABCD 61矩形S S AGC =∴∆．从而ABCDABCD 326121矩形矩形四边形）（S S S S S AGC ADC AGCD=+=+=∆∆．即ABCDAGCD S S 矩形四边形 =23 ．因此选D． 解二：连结AC 、BD ，AC 与BD 相交于点O ．则△ABC 的面积被分为6等份．同理可把△ADC 的面积等分为6份．显然四边形AGCD 占有8份，即O FEA BC D EFGAB CDEF GABCDAGCD S S 矩形四边形 32128==．因此选D ．2. 解析 分别取PA 、PB 的中点M 、N ，连结EM 、DM 、MN 、DN 、NF ，在Rt △AEP 中，EM =AM =MP ，又DM 为△ABP 的中位线，可得BP DM 21=．同理，FN =BN =NP ，且AP DN 21=，从而EM =DN ，DM =NF ．又∵DE=DF ，∴△EMD ≌△DNF ．∴∠EMD =∠DNF ．又∵∠1=∠3=∠2，∴∠AME =∠BNF ．从而可得∠PAE =∠PBF ．3．证明：如图，分别过点A 、B 作ED 、EC 的平行线,得交点P ,连△PBAPE .由AB // =CD ,易知≌△ECD .有PA ＝ED ，PB ＝EC .显然,四边形PBCE 、PADE 均为平行四边形.有∠BCE ＝∠BPE ，∠APE ＝∠ADE .由∠BAF ＝∠BCE ，可知∠BAF ＝∠BPE .有P 、B 、A 、E 四点共圆.于是,∠EBA ＝∠APE .所以,∠EBA ＝∠ADE .PE DGA B F C4．证明：延长CB 到D ，使BD =AB ，连结AD ，则AB +BD >AD ，即2AB >AD ．∵AB =BD ，∴∠BAD=∠D ．∴∠ABC =2∠D ．而∠ABC =2∠C ，∴∠C =∠D ．∴AC =AD ．∴2AB >AC ．5．解：设B 2到C 1A 1的垂线，C 2到A 1B 1的垂线相交于Q .则2222221221PB PA B C A C -=- （1） 2222221221PC PB C A B A -=- （2） 2222221221PA PC A B C B -=- （3） 2121212212QA QC A B C B -=- （4） 2121212212QB QA B C A C -=- （5）五式相加得2121221221QB QC A B A C -=- 即B B 11ACBDANCDEBM2121212212QB QC B A C A -=- 从而A 2Q ⊥B 1C 1.6.证明：如图，过点B 作AC 的平行线交ND 延长线于E .连ME .由BD ＝DC ，可知ED ＝DN .有△BED ≌△CND .于是，BE ＝NC .显然，MD 为EN 的中垂线.有EM ＝MN .由BM 2＋BE 2＝BM 2＋NC 2＝MD 2＋DN 2＝MN 2＝EM 2，可知△BEM 为直角三角形，∠MBE ＝90°.有∠ABC ＋∠ACB ＝∠ABC ＋∠EBC ＝90°.于是，∠BAC ＝90°.所以，AD 2＝221⎪⎭⎫ ⎝⎛BC ＝41(AB 2＋AC 2).7．证明：设AF 的延长线交AEF =△BDF 于K ，∵∠∠AKB ，∴∆AEF ≌∆AKB ．因此,EK BK AE AKAF AB AF AB==.于是要证（1），只需证明：(2)CD BK DF AK BD AB ⋅+⋅=⋅ 又注意到KBD KFD C ∠=∠=∠. 我们有1sin 2DCKSCD BK C ∆=⋅⋅∠，进一步有1sin 21sin 2ABD ADKS BD AB C S AK DF C ∆∆=⋅⋅∠=⋅⋅∠，因此要证（2），只需证明ABDDCK ADKS S S ∆∆∆=+（3）而（3）//(4)ABCAKCS S BK AC ∆∆⇔=⇔事实上由BKA FDB KAC ∠=∠=∠知（4）成立，得证. 8.证明：连结OA ，OD ，并延长OD 交△ABC 的外接圆于M ，则OD ⊥BC ，BM︿＝MC ︿，∴A 、E 、M 三点共线.∵AE 、AF 分别是△ABC 的∠A 及其外角平分线，∴AE ⊥AF .又∵HE ⊥AE ，HF ⊥AF ，∴四边形AEHF 为矩形.因此AH 与EF 互相平分，设其交点为G ，于是：AG ＝12 AH ＝12 EF ＝EG .而OA ＝OM ，且OD ∥AH ，∴∠OAM ＝∠OMA ＝∠MAG ＝∠GEA .故EG ∥OA (1) ∵O 、H 分别是△ABC 的外心和垂心，且OD ⊥BC ，∴OD ＝12 AH ＝AG ，因此，若连结DG ，则四边形AODG 为平行四边形 从而DG ∥OA . (2)由(1)和(2)知，D 、E 、G 三点共线，但F 在EG 上，故D 、E 、F 三点共线.“习题16”解答：··P OA BCD1．解：答案是PB =42㎝.连接OA ，OB .易知O ，P ，A ，B 四点共圆，有∠APB =∠AOB =90°.故PA 2+PB 2=AB 2=1989.由于PA :PB =5:14，可求PB .2.证明：如图,延长AD 与△ABC 的外接圆相交于点F ,连结CF 与BF ,则∠BFA ＝∠BCA ＝∠ABC ＝∠AFC ,即∠BFD ＝∠CFD .故BF :CF＝BD :DC .又∠BEF ＝∠BAC ,∠BFE ＝∠BCA ,从而∠FBE ＝∠ABC ＝∠ACB ＝∠BFE .故EB ＝EF .作∠BEF 的平分线交BF 于G ,则BG ＝GF .因∠GEF ＝21∠BEF ＝∠CEF ,∠GFE ＝∠CFE ,故△FEG ≌△FEC .从而GF ＝FC .于是,BF ＝2CF .故BD ＝2CD .3.提示：连结BP '、P'R 、P'C 、P'P ，（1）证四边形APPQ 为平行四边形；（2）证点A 、R 、Q 、P'共圆；（3）证△BP'Q 和△P'RC 为等腰三角形；（4）证∠P'BA =∠ACP '，原题得证. 4.略.5.证明：如图,过点P 作AB 的平行线交BDAN E BK G C D M F P AB GCD FE于F ,过点F 作BC 的平行线分别交PQ 、AC 于K 、G ,连PG .由BD 平行∠ABC ,可知点F 到AB 、BC 两边距离相等.有KQ ＝PN .显然,PD EP＝FDEF ＝GD CG ,可知PG ∥EC .由CE 平分∠BCA ,知GP平分∠FGA .有PK ＝PM .于是,PM ＋PN ＝PK ＋KQ ＝PQ .6.提示：证B ，Q ，E ，P 和B ，D ，E ，P 分别共圆。