2012年1月管理综合联考数学试题
- 格式:pdf
- 大小:147.72 KB
- 文档页数:3


管理类专业学位联考综合能力数学(应用题)-试卷1(总分:66.00,做题时间:90分钟)一、问题求解(总题数:33,分数:66.00)1.某商品的定价为200元,受金融危机的影响,连续两次降价20%后的售价为( ).A.114元B.120元C.128元√D.144元E.160元200×(1-0.2) 2 =128(元).2.银行的一年期定期存款利率为10%,某人于1991年1月1日存入10000元,1994年1月1日取出,若按复利计算,他取出时所得的本金和利息共计是( ).A.10 300元B.10 303元C.13 000元D.13 310元√E.14 641元10 000×(1+10%) 3 =13 310(元).3.某容器中装满了浓度为90%的酒精,倒出1升后用水将容器充满,搅拌均匀后又倒出1升,再用水将容器注满,已知此时的酒精浓度为40%,则该容器的容积是( ).A.2.5升B.3升√C.3.5升D.4升E.4.5升设容器的容积为V V=3.4.向一桶盐水中加入一定量水后,盐水浓度降到3%,又加入同样多的水后,盐水浓度又降到2%,则如果再加入同样多的水,盐水浓度应为( ).A.1.5%√B.1.2%C.1.1%D.1%E.0.5%设3%的盐水共有100克,含盐3克,加水x,则有解得x=505.一满桶纯酒精倒出10升后,加满水搅匀,再倒出4升后,再加满水.此时,桶中的纯酒精与水的体积之比是2:3.则该桶的容积是( )升.A.15B.18C.20 √D.22E.25设该桶的容积为x x=20.6.某种新鲜水果的含水量为98%,一天后的含水量降为97.5%.某商店以每斤1元的价格购进了1 000斤新鲜水果,预计当天能售出60%,两天内售完.要使利润维持在20%,则每斤水果的平均售价应定为( )元.A.1.20B.1.25C.1.30 √D.1.35E.1.40将果肉看作溶质,将水看作溶剂,将此水果看作溶液;设定价为每斤x元,根据题意,得每1斤的含水量为98%,则果肉质量为1×(1-98%)=0.02(斤);一天后每1斤水果的含水量为97.5%,则果肉占2.5%,总质量变为=0.8(斤)解得x=1.3.7.一种溶液,蒸发掉一定量的水后,溶液的浓度为10%;再蒸发掉同样多的水后,溶液的浓度变为12%;第三次蒸发掉同样多的水后,溶液的浓度变为( ).A.14%B.15%√C.16%D.17%E.18%设浓度10%时,溶液的体积为x,蒸发掉水分的体积为y,根据题意得解得根据溶质守恒定律,溶质的量始终为10%x;故再次蒸发掉同样多的水后,浓度为8.甲杯中有纯酒精12克,乙杯中有水15克,将甲杯中的部分纯酒精倒入乙杯,使酒精与水混合,然后将乙杯中的部分混合溶液倒入甲杯,此时,甲杯的浓度为50%,乙杯的浓度为25%.则从乙杯倒入甲杯的混合溶液为( )克.A.13B.14 √C.15D.16E.17设从甲杯中倒入乙杯的酒精为x克,则有设从乙杯倒入甲杯的混合溶液为y9.用含盐10%的甲盐水与含盐16%的乙盐水混合制成含盐11%的盐水600克,则用甲盐水( )克.A.200B.250C.300D.400E.500 √10.已知甲桶中有A农药50L,乙桶中有A农药40L,则两桶农药混合,可以配成农药浓度为40%的溶液.(1)甲桶中有A农药的浓度为20%,乙桶中A农药的浓度为65%. (2)甲桶中有A农药的浓度为30%,乙桶中A农药的浓度为52.5%.A.B.C.D. √E.条件(1):混合后农药浓度为条件(1)充分.条件(2)(2)充分.11.某年级60名学生中,有30人参加合唱团、45人参加运动队,其中参加合唱团而未参加运动队的有8人,则参加运动队而未参加合唱团的有( ).A.15人B.22人C.23人√D.30人E.37人如图5-4所示.参加合唱团且参加运动队的有30—8=22(人);参加运动队而未参加合唱团的有45—22=23(人).12.某年级举行数理化三科竞赛,已知参加数学竞赛的有203人,参加物理竞赛的有179人,参加化学竞赛的有165人;参加数学物理两科的有143人,参加数学化学两科的有116人,参加物理化学两科的有97人;三科都参加的有89人;则参加竞赛的总人数为( ).A.280 √B.250C.300D.350E.400由题意,可得 A∪B∪C=A+B+C—A ∩B-A ∩ C—B ∩ C+A ∩ B ∩ C =203+179+165-143-116-97+89=280.13.某公司的员工中,拥有本科毕业证,计算机等级证,汽车驾驶证的人数分别为130,110,90,又知只有一种证的人数为140,三证齐全的人数为30,则恰有双证的人数为( ).A.45B.50 √C.52D.65E.100由题意可以把证件分为三类:单证,双证,三证;三类证件的个数之和等于证件的总个数,设有双证的人数为x,则有 140+2x+30 × 3=130+110+90.解得x=50.14.电视台向100个人调查昨天收看电视情况,有62人看过中央一套,34人看过湖南卫视,11人两个频道都看过.则两个频道都没有看过的有( )人.A.4B.15 √C.17D.28E.24两个频道都没有看过的有:100-(62+34—11)=15(人).15.甲商店销售某种商品,该商品的进价每件90元,若每件定价100元,则一天内能售出500件,在此基础上,定价每增1元,一天少售出10件,若使甲商店获得最大利润,则该商品的定价应为( ).A.115元B.120元√C.125元D.130元E.135元设定价比原定价高了x元,利润为y元,根据题意得y=(100+x一90)(500一10x) =10×(500+40x一x 2) =一10(x 2一40x+400-900) =一10(x一20) 2 +9000,根据一元二次函数的性质,可知当x=20时,利润最高,此时定价为120元.16.已知某厂生产x件产品的成本为C=25 元),若产品以每件500元售出,则使利润最大的产量是( ).A.2 000件B.3 000件C.4 000件D.5 000件E.6 000件√6 000件.17.某产品的产量Q与原材料A,B,C的数量x,y,z(单位均为吨)满足Q=0.05xyz,已知A,B,C每吨的价格分别是3,2,4(百元).若用5 400元购买A,B,C三种原材料,则使产量最大的A,B,C的采购量分别为( ).A.6,9,4.5吨√B.2,4,8吨C.2,3,6吨D.2,2,2吨E.以上结果均不正确设A,B,C的采购量分别为x吨、y吨、z吨,由题意可知3x+2y+4z=54,由均值不等式,可知当3x=2y=4z时等号成立,解得x=6,y=9,z=4.5.18.一辆中型客车的营运总利润y(单位:万元)与营运年数x(x∈N)的变化关系如表5-2所示,则客车的运输年数为( )时该客车的年平均利润最大.A.4年B.5年√C.6年D.7年E.8年由题干可知二次函数y=ax 2 +bx 2 +c过三点(4,7)、(6,11)、(8,7),故有故有y=一x 2 +12x 2-25.19.某产品的产量Q与原材料A,B,C的数量x,y,z(单位:吨)满足Q=0.05xyz,已知A,B,C每吨的价格分别是3,2,4(百元).若用5 400元购买A,B,C三种原材料,则使产量最大的A,B,C的采购量分别为( ).A.6,9,4.5吨√B.2,4,8吨C.2,3,6吨D.2,2,2吨E.以上结果均不正确设A,B,C的采购量分别为x吨、y吨、z吨,由题意可知3x+2y+4z=54,3x=2y=4z 时等号成立,解得x=6,y=9,z=4.5.20.如图5-7所示,在矩形ABCD中,|AB|=6cm,|BC|=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动,则五边形APQCD的面积的最小值为( ).A.48B.52C.60D.63 √E.69五边形APQCD =6 × 12一(一t 2+6t)=t 2一6t+72=(t 一3) 2+63(0<t <6), 故当t=3时,S 五边形APQCD的最小值为63.21.如图5—8所示,在一个直角△MBN 的内部作一个长方形ABCD ,其中AB 和BC 分别在两直角边上,设|AB|=xm ,长方形的面积为y m 2,要使长方形的面积最大,其边长x 应为( ).A.3 mB.6 mC.15 mD.2.5 m √E.9 m|AB|=xm ,|AD|=bm ,长方形的面积为y m 2,因为AD ∥BC ,故 , 所以 当x=2.5时,y 有最大值.22.某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2 000平方米的楼房.经测算,如果将楼房建为x(x ≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为( )层.(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=)A.10B.12C.13D.15 √E.16设楼房每平方米的平均综合费为f(x)23.某汽车4S 店每辆20万元的价格从厂家购入一批汽车,若每辆车的售价为m 万元,则每个月可以卖(300--10m)辆汽车,但由于国资委对汽车行业进行反垄断调查,规定汽车的零售价不能超过进价的120%,该4S 店计划每月从该种汽车的销售中赚取至少90万元,则其定价最低应设为( )万元. A.21 √ B.22 C.23 D.24 E.25设最低定价为x 21万元.24.某工厂生产一种产品的固定成本为2 000元,已知每生产一件这样的产品需要再增加可变成本10元,又知总收入K 是单位产品数Q 的函数,K(Q)=40Q —Q 2,则总利润L(Q)的最大时,应该生产该产品( ). A.5件 B.10件 C.15件 √ D.20件 E.25件由题意得,利润为 L(Q)=40Q —Q 2—2 000—10Q=一Q 2+30Q 一2000,25.某公司计划运送180台电视机和110台洗衣机下乡,现在两种货车,甲种货车每辆最多可载40台电视机和10台洗衣机,乙种货车每辆最多可载20台电视机和20台洗衣机,已知甲、乙种货车的租金分别是每辆400元和360元,则最少的运费是( ).A.2 560元B.2 600元√C.2 640元D.2 580元E.2 720元设用甲种货车x辆,乙种货车y辆,总费用为z若x=2,y=5,费用为800+360×5=2 600(元);若x=3,y=4,费用为1 200+360×4=2 640(元);可知用甲车2辆,乙车5辆时,费用最低,是2 600元.26.某家具公司生产甲、乙两种型号的组合柜,每种柜的制造白坯时间、油漆时间及有关数据如表5-3所示:则该公司每天可获得的最大利润为( ).A.2 560元B.2 720元√C.2 820元D.3 000元E.3800元设x,y分别为甲、乙两种柜的日产量,则目标函数为z=200x+240y;线性约束条件为用先取边界后取整数法,将不等式取等号得故z max =200×4+240×8=2 720(元).27.某公司每天至少要运送270吨货物.公司有载重为6吨的A型卡车和载重为10吨的B型卡车,A型卡车每天可往返4次,B型卡车可往返3次,A型卡车每天花费300元,B型卡车每天花费500元,若最多可以调用10辆车,则该公司每天花费最少为( ).A.2 560元B.2 800元C.3 500元D.4 000元√E.48 00元设用A型卡车x辆,B型卡车y辆,根据题意有目标函数为z=300x+500y.用先取边界后取整数法,将不等式取等号得故每天最少花费为z min =300×5+500 × 5=4 000(元).28.某公司每天至少要运送180吨货物.公司有8辆载重为6吨的A型卡车和4辆载重为10吨的B型卡车,A型卡车每天可往返4次,B型卡车可往返3次,A型卡车每天花费320元,B型卡车每天花费504元,若最多可以调用10辆车,则该公司每天花费最少为( ).A.2 560元√B.2 800元C.3 500元D.4 000元E.4 800元设用A型卡车x辆,B型卡车y辆,根据题意有目标函数为z=320x+504y.可行域为图5—9中阴影区域.做直线l’:320x+504y=0.在可行域中打上网格,找出(8,0)、(8,1)、(8,2)、(7,1)、(7,2)、(7,3)等整数点.作l:320x+504y=t与l’平行,可见当l过(8,0)时t最小,即z min=8×320=2 560(元).29.某糖果厂生产A,B两种糖果,A种糖果每箱获利润40元,B种糖果每箱获利润50元,其生产过程分为混合、烹调、包装三道工序,表5-4为每箱糖果生产过程中所需平均时间(单位:分钟)每种糖果的生产过程中,混合的设备至多能用12机器小时,烹调的设备至多只能用机器30机器小时,包装的设备只能用机器15机器小时,则该公司获得最大利润时,应该生产B糖果( )箱.A.200B.260C.280D.300 √E.320用图像法求可行域.设生产A种糖果x箱,B种糖果y箱,可获得利润z元,且12小时=720分钟,30小时=1 800分钟,15小时=900分钟.则约束条件为即在图5—10所示阴影部分内,求目标函数z=40x+50y的最大值.整理得的平行直线系,当此直线过C点时,纵截距最大,故此时z有最大值.解方程组故z max =40×120+50×300=19 800(元).即生产A种糖果120箱,生产B种糖果300箱,可得最大利润19 800元.30.某自来水公司的消费标准如下:每户每月用水不超过5吨的,每吨收费4元,超过5吨的,收较高的费用.已知9月份张家的用水量比李家多50%,张家和李家的水费分别为90元和55元,则用水量超过5吨时的收费标准是( )元/吨.A.5B.5.5C.6D.6.5E.7 √每户消费的前5吨水的费用为20元,可见张家和李家9月用户量都超过了5吨.设超过5吨时的收费标准是x,9月李家用水量为y吨,则张家用水量为1.5y吨.根据题意,得解得x=7,y=10,所以超过5吨时的收费标准为7元/吨.31.某商场在一次活动中规定:一次购物不超过100元时没有优惠;超过100元而没有超过200元时,按该次购物全额9折优惠;超过200元时,其中200元按9折优惠,超过200元的部分按8.5折优惠.若甲、乙两人在该商场购买的物品分别付费94.5元和197元,则两人购买的物品在举办活动前需要的付费总额是( )元.A.291.5B.314.5C.325D.291.5和314.5E.314.5或325 √甲有两种情况: (1)甲没有得到优惠,则甲的购物全额为94.5元; (2)甲得到了9折优惠,则甲的购物全额为=105(元);乙的200元得到了9折优惠,实际付款180元,余下的部分按8.5折优惠,故此部分的购物全额为=20(元);故乙的购物全额为200+20=220(元) 所以两人在活动前需要付费总额为94.5+220=314.5(元),或者,105+220=325(元).32.税务部门规定个人稿费纳税办法是:不超过1 000元的部分不纳税,超过1 000而不超过3 000元的部分按5%纳税,超过3 000元的部分按稿酬的10%纳税,一人纳税450元,则此人的稿费为( )元.A.6 500 √B.5 500C.5 000D.4 500E.4 000超过1 000不超过3 000的部分需纳税:2 000×5%=100(元);说明超过3 000元的部分此人交了350元的税,故=3 500(元);所以此人的稿费为1 000+2 000+3 500=6 500(元).33.某市居民用电的价格为:每户每月不超过50度的部分,按0.5元1度收费;超过50度不到80度的部分,按照0.6元1度收费;80度以上的部分,按0.8元1度收费;隔壁老王这个月一共交了电费139元,则这个月老王一共用电( )度.A.180B.200 √C.210D.220E.225不超过50度的部分:50×0.5=25(元);50度以上到80度的部分:30×0.6=18(元).可知,80度上的部分,老王花费:139—25—18=96(元).故80度以上的部分,老王用电:=120(度),故老王一共用电:50+30+120=200(度).。

2014年1月管理类专业学位联考综合能力(数学)真题试卷(题后含答案及解析)题型有:1. 问题求解 2. 条件充分性判断问题求解1.某部门在一次联欢活动中共设了26个奖,奖品均价为280元,其中一等奖单价为400元,其他奖品均价为270元,一等奖的个数为( ).A.6B.5C.4D.3E.2正确答案:E解析:设一等奖个数为x,得400x+(26一x)×270=280×26,得出x=2.2.某单位进行办公室装修,若甲、乙两个装修公司合做,需10周完成,工时费为100万元;甲公司单独做6周后由乙公司接着做18周完成,工时费为96万元.甲公司每周的工时费为( ).A.7.5万元B.7万元C.6.5万元D.6万元E.5.5万元正确答案:B解析:设甲、乙每周工时费分别为x,y万元,列方程组3.如图1所示,已知AE=3AB,BF=2BC,若△ABC的面积是2.则△AEF 的面积为( ).A.14B.12C.10D.8E.6正确答案:B解析:根据两个三角形的高相同,则面积的比就是底边的比,S△ABC=2→S△ACF=2→S△FBE=8,所以S△AEF=2+2+8=12.4.甲、乙两人上午8:00分别自A,B出发相向而行,9:00第一次相遇,之后速度均提升了1.5 km/h,甲到B、乙到A后都立刻原路返回,若两人在10:30第二次相遇,则A,B两地的距离为( ).A.5.6 kmB.7 kmC.8 kmD.9 kmE.9.5 km正确答案:D解析:设甲、乙两人的速度分别为V甲、V乙,列方程组,消去V甲+V乙,得出S=9.5.如图2所示,圆A与圆B的半径均为1,则阴影部分的面积为( ).A.B.C.D.E.正确答案:E解析:如图1所示,根据对称性,得S阴影=2(S扇形CAD一S△CAD),即.6.已知{an}为等差数列,且a2一a5+a8=9,则a1+a2+…+a9=( ).A.27B.45C.54D.8:1E.1 62正确答案:D解析:a2—a5+a8=9,得a5=9,S9==9a5=81.7.某容器中装满了浓度为90%的酒精,倒出1 L后用水将容器注满,搅拌均匀后又倒出1 L,再用水将容器注满,已知此时的酒精浓度为40%,则该容器的容积是( ).A.2.5 LB.3 LC.3.5 LD.4 LE.4.5 L正确答案:B解析:设容器容积为xL,列方程组0.9x一1×0.9—=0.4x,得出x=3.8.某公司投资一个项目,已知上半年完成了预算的,下半年完成了剩余部分的,此时还有8千万元投资未完成,则该项目预算为( ).A.3亿元B.3.6亿元C.3.9亿元D.4.5亿元E.5.1亿元正确答案:B解析:设该项目预算为x千万元,则+8 000=x,得出x=3.6亿.9.在某项活动中,将3男3女6名志愿者随机地分成甲、乙、丙三组,每组2人,则每组志愿者都是异性的概率为( ).A.B.C.D.E.正确答案:E解析:体育比赛中的分组问题,古典概型P(A)=.10.已知直线l是圆x2+y2=5在点(1,2)处的切线,则l在y轴上的截距为( ).A.B.C.D.E.正确答案:D解析:点(1,2)在圆x2+y2=5上,根据总结的结论:切线方程为x0x+y0y=5,代入可得x+2y一5→y=一,即在y轴上截距为.11.某单位决定对4个部门的经理进行轮岗,要求每位经理必须轮换到4个部门中的其他部门任职,则不同的轮岗方案有( ).A.3种B.6种C.8种D.9种E.10种正确答案:D解析:根据总结的结论,这是4个元素的错位排列,答案为9.12.如图3所示,正方体ABCD—A’B’C’D’的棱长为2,F是棱C’D’的中点,则AF的长为( ).A.3B.5C.D.E.正确答案:A解析:如图2所示,连结AD则AF=.13.某工厂在半径5 cm的球形工艺品上镀一层装饰金属,厚度为0.01 cm,已知装饰金属的原材料是棱长为20 cm的正方体锭子,则加工10 000个该工艺品需要的锭子数最少为( ).(不考虑加工损耗,π≈3.14)A.2B.3C.4D.5E.20正确答案:C解析:根据球与正方体体积公式,该工艺品需要锭子数量为14.若几个质数(素数)的乘积为770,则它们的和为( ).A.85B.84C.28D.26E.25正确答案:E解析:分解质因数770=2×5×7×11.15.掷一枚均匀的硬币若干次,当正面向上次数大于反面向上次数时停止,则在4次之内停止的概率为( ).A.B.C.D.E.正确答案:C解析:在4次以内停止含两种情况:第一次正面,第一、二、三次依次为反面、正面、正面,则P(A)=.条件充分性判断16.设x是非零实数,则x3+=18.A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.正确答案:A解析:题干.条件(1),x+=3,代入条件(1)充分.条件(2),,条件(2)不充分.17.甲、乙、丙三人年龄相同.(1)甲、乙、丙三人年龄成等差数列.(2)甲、乙、丙三人年龄成等比数列.A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.正确答案:C解析:明显需要联合,同时是等差和等比数列的只能是非零的常数数列,选C.18.不等式|x2+2x+a|≤1的解集为空集.(1)a<0.(2)a>2.A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.正确答案:B解析:由题干得一1≤x2+2x+a≤1,即一1≤(x+1)2+a一1≤1,数形结合,如图3所示,考虑图像开口向上与顶点纵坐标(一1,a一1),一1≤(x+1)2+a一1≤1无解,观察得a一1>1即a>2;(1)不充分;(2)充分.19.已知曲线l:y=a+bx一6x2+x3,则(a+b一5)(a一b一5)=0.(1)曲线l过点(1,0).(2)曲线l过点(一1,0).A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.正确答案:A解析:题干(a+b一5)(a一b—5)=0a+b=5或a一b=5.由条件(1)代入(1,0)可得a+b=5,充分;由条件(2)代入(一1,0)可得a—b=7,不充分.20.如图4所示,O是半圆的圆心,C是半圆上的一点,OD⊥AC,则能确定OD的长.(1)已知BC的长.(2)已知OA的长.A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.正确答案:A解析:因为AB为半圆0的直径,故∠C为直角,又OD⊥AC,O为AB中点,条件(1),由三角形中位线定理,可知BC=20D,充分;条件(2)不充分.21.已知x,y为实数,则x2+y2≥1.(1)4y一3x≥5.(2)(x一1)2+(y 一1)2≥5.A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.正确答案:A解析:如图4所示,条件(1)4y一3x≥5表示的平面区域到原点最短距离d=1,故x2+y2≥1,(1)充分;如图5所示,条件(2)表示(x一1)2+(y一1)2≥5表示区域是圆心在(1.1),半径为的圆及其外部,到原点最短距离|OA|=r—|OC|=≈0.822,故条件(2)不充分.22.已知袋中装有红、黑、白三种颜色的球若干个,则红球最多.(1)随机取出的一球是白球的概率为.(2)随机取出的两球中至少有一个的黑球概率小于.A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.正确答案:C解析:条件(1)由,不充分;条件(2)“随机取出两球中至少有一个是黑球概率”大于“随机取出1个球是黑球的概率”,即“随机取出1个球是黑球的概率”小于,不充分;条件(1)和(2)条件联合:白球占总数的,充分。

管理类专业学位联考综合能力数学(不等式)历年真题试卷汇编1(总分:52.00,做题时间:90分钟)一、问题求解(总题数:6,分数:12.00)1.[2016年12月]不等式|x一1|+x≤2的解集为( )。
(分数:2.00)A.(—∞,1]B.(√C.[1D.[1,+∞)解析:解析:本题考查含有绝对值的不等式的求解。
方法一:数形结合。
将不等式|x一1|+x≤2变形为|x一1|≤2—x,在平面直角坐标系中,画出y=|x一1|和y=2—x的图像,如下图所示,可知原不等式的解集为(一∞,]。
方法二:去绝对值。
当x≥1时,原不等式变为x一1+x≤2,解得x≤;当x<1时,原不等式变为1—x+x≤2,即1≤2,它是恒成立的。
所以不等式的解集为(一∞,]。
2.[2014年12月]设A(0,2),B(1,0),在线段AB上取一点M(x,y)(0<x<1),则以x,y为两边长的矩形面积最大值为( )(分数:2.00)A.B. √C.D.E.解析:解析:设点M所在的直线为y=kx+b,则将A、B两点坐标代入直线方程可得b=2,k=一2。
所以点M所在的直线为y=一2x+2,即2x+y=2。
根据均值不等式,当2x—y=1,即x=,y=1时,矩形面积最大。
3.[2012年10月]4对x∈(0,+∞)恒成立,则a的取值范围是( )。
(分数:2.00)A.(一∞,—1)B.(1,+∞)C.(—1,1)D.(—1,+∞)E.(1,+∞)∪(一∞,一1) √解析:解析:不等式4(x>0)→f(x)=x 2—2x+a 2>0恒成立,因此方程f(x)=0的△=4—4a 2<0=a>1或a<一1,因此选E。
4.[2010年10月]若y 2—<0对一切实数x恒成立,则y的取值范围是( )。
(分数:2.00)A.1<y<3 √B.2<y<4C.1<y<4D.3<y<5E.2<y<52,解不等式得1<y<3。
5.[2008年1月]直角边之和为12的直角三角形面积最大值等于( )。

MBA联考综合能力数学(浓度问题、容斥问题、利润问题)历年真题试卷汇编1(总分:58.00,做题时间:90分钟)一、问题求解(总题数:19,分数:38.00)1.问题求解本大题共15小题。
下列每题给出的五个选项中,只有一项是符合试题要求的。
__________________________________________________________________________________________ 2.[2014年1月]某容器中装满了浓度为90%的酒精,倒出1升后用水将容器注满,搅拌均匀后又倒出1升,再用水将容器注满。
已知此时的酒精浓度为40%,则该容器的容积是( )。
A.2.5升B.3升√C.3.5升D.4升E.4.5升在类似的重复倒出加水稀释的过程中,溶液的浓度,每一次都是按固定比例变化的。
浓度由90%经过两次稀释,变为40%,则每次变化的比例是2/3。
由于溶液质量不变,浓度变为2/3,则溶质的量减少1/3,即倒出的1升占容积的1/3,因此该容器的容积为3升,选B。
3.[2012年10月]一满桶纯酒精倒出10升后,加满水搅匀,再倒出4升后,再加满水。
此时,桶中的纯酒精与水的体积之比是2:3。
则该桶的容积是( )。
A.15升B.18升C.20升√D.22升E.25升设容积为x升,则第一次酒精为x一10升,水为10升,总量为x升;第二次酒精为x一10x=2:(2+3),解得x=20,因此选C。
4.[2011年10月]含盐12.5%的盐水40千克蒸发掉部分水分后变成了含盐20%的盐水,蒸发掉的水分重量为( )。
A.19千克B.18千克C.17千克D.16千克E.15千克√设蒸发掉的水分重量为x%,解得x=15。
5.[2009年1月]在某实验中,三个试管各盛水若干。
现将浓度为12%的盐水10克倒入A管中,混合后,取10克倒入B管中,混合后再取10克倒入C管中,结果A、B、C三个试管中盐水的浓度分别为6%、2%、0.5%,那么三个试管中原来盛水最多的试管及其盛水量分别是( )。
2012年MBAMPA 管理类联考:综合能力数学:串讲精要充分性判断的解题说明本题要求判断所给出的条件能否充分支持题干中陈述的结论。
阅读每小题中的条件(1)和(2)后选择: A .条件(1)充分,但条件(2)不充分 B .条件(2)充分,但条件(1)不充分C .条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分D .条件(1)充分,条件(2)也充分E .条件(1)和(2)单独都不充分,条件(1)(2)联合起来也不充分解题指导思想:抓住“充分性”这一本质:由(1)(2)这样的条件推出题设成立才叫“充分性” 解题有三种方法可以应用。
(1)由下到上法:最本质的方法,“充分性”概念的体现。
(2)由上到下法:逆向思维,当题设推出的等价结论包含或者等于给出的条件时,“充分性”才可以成立。
(3)双向法:上面两种方法的结合。
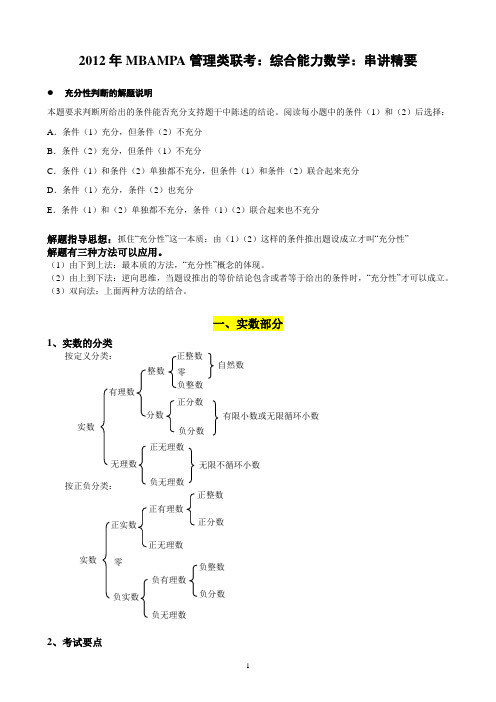
一、实数部分1、实数的分类按定义分类:按正负分类:2、考试要点实数有理数无理数整数分数正整数 零 负整数 正分数负分数自然数有限小数或无限循环小数 正无理数负无理数无限不循环小数 实数正实数负实数零正整数负整数正分数负分数 负有理数负无理数正有理数正无理数(1)最小的质数是2, (2)最小的合数是4(3)大于2的质数必为奇数,即只有2是偶质数 (4)1既不是质数也不是合数(8)如果两个质数的和或差是奇数,那么必有一质数为2 (9)如果两个质数的积是偶数,那么必有一质数为2(10)整除关系(能被2,3,4,5,6,8,9,10,11,12整除) (17)最简分数(既约分数)(18)循环小数化为分数的方法:根据循环节的位数用9,99,999等等做为分母。
循环节上的数字作为分子。
2、典型题目例1:∙∙∙∙∙456.0,36.0,7.0例2:已知3个质数的倒数和为1661/1986,则这三个质数的和为( )二、整式与分式一、因式分解常用公式()=±2b a ()=±3b a22b a -=±33b a=++2)(c b a (重要)=---++ac bc ab c b a 222 (重要)例:已知n 为整数,2≥n ,则n n -3必有约数( )(A)5 (B)6 (C)7 (D)8 (E )9二、因式定理与余式定理整式的除法:如果()x f 除以()x g ,商式为()x Q ,余式为()x R ,则()=x f ()x g ()x Q +()x R 1:余式定理:多项式()x f 除以()a x -的余式为()a f ()x f 除以()b ax -的余式为⎪⎭⎫⎝⎛a b f 2:因式定理:相当于余式定理中余式为0的情况。
管理类专业学位联考综合能力数学(实数的性质及运算;绝对值、根式、完全平方式)历年真题试卷汇编1(题后含答案及解析)题型有:1. 问题求解 2. 条件充分性判断问题求解1.[2016年12月]将长、宽、高分别为12、9、6的长方体切割成正方体,且切割后无剩余,则能切割成相同正方体的最少个数为( )。
A.3B.6C.24D.96E.648正确答案:C解析:本题考查空间几何体。
当所切割成的正方体棱长为原长方体长、宽、高的最大公约数时切割后无剩余,且得到的相同正方体的个数最少。
12、9、6的最大公约数为3,所以正方体的最少个数为(12÷3)×(9÷3)×(6÷3)=24。
知识模块:实数的性质及运算2.[2014年12月]设m,n是小于20的质数,满足条件|m—n|=2的{m,n}共有( )。
A.2组B.3组C.4组D.5组E.6组正确答案:C解析:20以内的质数是2,3,5,7,11,13,17,19,其中|3—5|=2,|5—7|=2,|11—13|=2,|17—19|=2,所以满足要求的{m,n}有4组,选择c选项。
知识模块:实数的性质及运算3.[2014年1月]若几个质数(素数)的乘积为770,则它们的和为( )。
A.85B.84C.28D.26E.25正确答案:E解析:因为已知若干质数的乘积为770,因此将770分解质因数可得770=2×5×7×11,显然2、5、7、11均为质数,故它们的和为2+5+7+11=25,故选E。
知识模块:实数的性质及运算4.[2011年1月]设a、b、c是小于12的三个不同的质数(素数),且|a—b|+|b—c|+|c—a|=8,则a+b+c=( )。
A.10B.12C.14D.15E.19正确答案:D解析:小于12的质数有2,3,5,7,11,则由|a—b|+|b一c|+|c一a|=8,且如果这三个数中有11的话,11与其他任意两数差的绝对值相加,结果必然大于8,与已知相矛盾;同时,也不可能有2这个数,因为两两差的绝对值显然不等于8,所以a、b、c这三个数为3、5、7,则a+b+c=3+5+7=15。
中原六校联谊 2012年高三第一次联考数学试题(文科)考试时间:150分钟 试卷满分:150分本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,其中第II 卷第(22)~(24)题为选考题,其他题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项1.答题前,考生务必先将自己的姓名,准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号,非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整,笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卷面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
参考公式:样本数据n x x x ,,,21 的标准差;x x x x x x x ns n 其中],)()()[(122221-+-+-=为样本平均数; 柱体体积公式:为底面面积其中S Sh V ,=、h 为高;锥体体积公式:h S Sh V ,,31为底面面积其中=为高; 球的表面积、体积公式:,34,432R V R S ππ==其中R 为球的半径。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,3,5,7,9),B={0,3,6,9,12),则N A B ð =( )A .{l,5,7}B .{3,5,7)C .{1,3,9)D .{l,2,3}2.己知i 为虚数单位,则1i i+=( )A .12i- B .12i+ C .12i-- D .12i-+ 3.设α、β为两个不同的平面,m 、n 为两条不同的直线,且,m n αβ⊂⊂,有两命题:p :若m//n ,则α∥β;q :若m ⊥β,则α⊥β;那么 ( ) A .“p 或q ”是假命题 B .“p 且q ”是真命题 C .“非p 或q ”是假命题 D .“非p 且q ”是真命题 4.“m<l ”是“函数f (x )=x +x+m 有零点”的( ) A .充分非必要条件 B . 充要条件 C .必要非充分条件 D . 非充分必要条件5.已知函数f (x )=(cos 2x cos x+sin 2x sin x ) sin x ,x ∈R ,则f (x )是( ) A .最小正周期为π的奇函数 B .最小正周期为π的偶函数 C .最小正周期为2π的奇函数 D .最小正周期为2π的偶函数 6.执行如图所示的程序框图,输出的S 值为( ) A .1 B .-1 C .-2 D .07.若某空间几何体的三视图如图所示,则该几何体的体积 A .202π-B .2203π-C .2403π-D .4403π-8.设{a n }是公比为q 的等比数列,令1(1,2,),{}n n n b a n b =+= 若数列的连续四项在集合{-53,-23,19,37,82}中,则q 等于( )A .3443--或 B .3223--或 C .32-D .43-9.变量x ,y 满足43035251x y x y x -+≤⎧⎪+≤⎨⎪≥⎩,目标函数z=2x+y ,则有( )A .min 3,z z =无最大值B .max 12,z z =无最小值C .max min 12,3z z ==D .z 既无最大值,也无最小值10.已知圆222()()x a y b r -+-=的圆心为抛物线y 2=4x 的焦点,且与直线3x+4y+2=0相切,则该圆的方程为( ) A .2264(1)25x y -+=B .2264(1)25x y +-=C .22(1)1x y -+=D .22(1)1x y +-=11.已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=+>><<为奇函数,该函数的部分图象如图所示,△EFG 是边长为2的等边三角形,则f (l )的值为 ( )A .B .CD .12.设f (x )与g (x )是定义在同一区间[a ,b]上的两个函数,若函数y=f (x )—g (x )在x ∈[a ,b]上有两个不同的零点,则称f (x )和g (x )在[a ,b]上是“关联函数”,区间[a ,b]称为“关联区间”.若f (x )=x 2—3x+4与g (x )=2x+m 在[0,3]上是“关联函数”,则m 的取值范围为 A .9(,2]4-- B .[—1,0]C .(,2]-∞-D .9(,)4-+∞第II 卷本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答,第22题~第2 4题为选考题,考试根据要求傲答。
管理类专业学位联考综合能力(数学)-试卷14(总分:50.00,做题时间:90分钟)一、问题求解(总题数:15,分数:30.00)1.A.B.C.D.E. √设,则E.2.设a,b,c为整数,且∣a一b∣20 +∣c一a∣41 =1,则∣a一b∣+∣a一c∣+∣b一c∣=( ).A.2 √B.3C.4D.一3E.一2由题设条件,a,b,c均为整数,所以a一b,c一a a=b,∣c—a∣=1,故∣b一c∣—∣c一a∣=1.由②得c=a,∣a一b∣=1,故∣a一b∣=∣c一b∣=1.在两种情形,都有∣b一c∣=1,且∣a一b∣+∣c一a∣=1 所以∣a一b∣+∣c一a∣+∣b一c∣=2 故本题应选A.3.某产品有一等品、二等品和不合格品三种,若在一批产品中一等品件数和二等品件数的比是5:3,二等品件数和不合格品件数的比是4:1,则该批产品的不合格品率约为 ( ).A.7.2%B.8%C.8.6%√D.9.2%E.10%由已知条件,一等品、二等品和不合格品的件数之比为20:12:3,C.4.设a>b>0,k>0,则下列不等式中能够成立的是( )A.B.C. √D.E.因为a>b>0,k>0,所以ak>bk.由此可得ab+ak>ab+bk,即 a(b+k)>b(a+k)C.5.P是以a为边长的正方形,P 1是以P的四边中点为顶点的正方形,P 2是以P 1的四边中点为顶点的正方形,…,P i是以P i一1的四边中点为顶点的正方形,则P 6的面积为 ( ).A.B.C.D.E. √如图22一1,可直接看出正方形P i的面积是正方形P i一1面积的,所以,正方形P的面积为a 2,则P 1的面积为,P 2的面积为,…,P 6的面积为故本题应选E.6.一批救灾物资分别随16列货车从甲站紧急调到600公里以外的乙站,每列车的平均速度都为125公里/小时.若两列相邻的货车在运行中的间隔不得小于25公里,则这批物资全部到达乙站最少需要的小时数为( ).A.7.4B.7.8 √C.8D.8.2E.8.4根据题设条件,两列相邻货车的发车时间应不少于(小时).所以,最后一列货车的发车时间比第一列货车发车时间至少晚15×0.2=3(小时).由此可知,这批物资全部到达乙站最少需故本题应选B.7.某工厂定期购买一种原料.已知该厂每天需用该原料6吨,每吨价格1800元,原料的保管等费用平均每吨3元,每次购买原料需支付运费900元.若该厂要使平均每天支付的总费用最省,则应该每( )天购买一次原料.A.11B.10 √C.9D.8E.7设工厂每x天购买一次原料,每天平均支付的总费用为y.由题意,每次购买的原料为6x吨,共需1800×6x元,x天内的保管费用为 3[6x+6(x一1)+6(x一2)+…+6×2+6×1]=9x(x+1) 于是,平均每天支付的总费用其中,当且仅当时,取等号.y可取得最小值,由此求得x=10.故本题应选B.8.x的取值范围是( ).A.x<0B.x≥一2C.x>2D.一2≤x≤0 √E.一2<x<02≤x≤0.故本题应选D.9.一个圆柱体的高减少到原来的70%,底半径增加到原来的130%,则它的体积 ( ).A.不变B.增加到原来的121%C.增加到原来的130%D.增加到原来的118.3%√E.减少到原来的91%设圆柱体原底半径为r,高为h,体积为V.变化后的体积为V′,则 V′=π(1.3r) 2·(0.7h)=1.183πr 2 h=1.183V 所以,它的体积增加到原来的118.3%.故本题应选D.10.若方程x 2 +px+q=0的一个根是另一个根的2倍,则P和q应满足( ).A.P 2 =4qB.2p=3q 2C.4p=9q 2D.2p 2 =9q √E.以上结论均不正确设方程x 2 +px+q=0的两根为x 1,x 2,且x 1 =2x 2,则x 1 +x 2 =一P,x 1 x 2 =q,即 3x 2 =一p,2xx 22 =q 由此可得,即2p 2 =9q.故本题应选D.11.已知等差数列{a n }的公差不为0,但第3,4,7项构成等比数列,则A. √B.C.D.E.设等差数列{a n }的首项为a 1,公差为d,则由a 24 =a 3 a 7,得 (a 1 +3d) 2 =(a 1 +2d)(a 1 +6d) 化简得3d 2 +2a 1 d=0.因为d≠0,有,于是故本题应选A.12.湖中有四个小岛,它们的位置恰好近似构成正方形的四个顶点.若要修建三座桥将这四个小岛连接起来,则不同的建桥方案有( )种.A.12B.16 √C.18D.20E.24四个小岛两两连接,需建C 24 =6座桥,从6座桥中选3座共有C 36 =20种方案,其中使3个小岛两两相连的方案有4种.所以,满足要求的不同的建桥方案有C 36—4=16种.故本题应选B.注:本题也可以直接枚举建桥方案如图22一2:图中,每一类建桥方案都各有4种不同的建桥方式.故符合要求的建桥方案有4×4=16种.13.一批灯泡共10只,其中有3只质量不合格.今从该批灯泡中随机取出5只,则这5只灯泡中只有3只合格的概率是( ).A.B.C. √D.E.设事件A={任取5只灯泡只有3只合格},则基本事件总数为C 510,事件A包含的基本事件数为C 37·C 23,于是,所求概率故本题应选C.14.某剧院正在上演一部新歌剧,前座票价为50元,中座票价为35元,后座票价为20元,如果购到任何一种票是等可能的,现任意购买到2张票,则其值不超过70元的概率为( ).A.B.C.D. √E.根据题意,在前座、中座、后座票中任购两张,共有3 2 =9种购票方案.现购到2张票,其值不超过70元的情形有(前,后),(中,中),(中,后),(后,前),(后,中),(后,后)6种,故所求概率为故本题应选D.15.过点A(2,0)向圆x 2 +y 2 =1作两条切线AM和AN(见图2—1),则两切线和弧MN所围成的面积(图中阴影部分)为( ).A.B.C.D.E. √如图22—3,连接OM,ON,则AN⊥ON,AM⊥OM.在△AON中,ON=1,AO=2,所以∠AON=60°.类似可得∠AOM=60°.且,所以四边形ANOM的面积故本题应选E.二、条件充分性判断(总题数:10,分数:20.00)16.ad>bc成立. (1)a+d=b+c (2)∣a—d∣<∣b一c∣A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.√D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.条件(1)不充分,例如,a=8,b=6,c=4,d=2满足a+d=b+c=10,但ad<bc.条件(2)不充分,例如,a=2,b=5,c=2,d=4时,满足∣a一d∣<∣b一c∣,但ad<bc.当条件(1)、(2)合在一起时,由条件(2),有∣a一d∣2<∣b一c∣2即a 2—2ad+d 2<b 2—2bc+c 2于是(a+d) 2一4ad<(b+c) 2一4bc 由条件(1),有(a+d) 2 =(b+c) 2,由上面的不等式,可得ad>bc 故本题应选C.17.A公司2003年6月份的产值是1月份产值的a倍. (1)在2003年上半年,A公司月产值的平均增长率为(2)在2003年上半年,A公司月产值的平均增长率为A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.√设A公司月产值的平均增长率为x,1月份产值为1,则6月份产值为1(1+x) 5=a,故(1)和条件(2)均不充分.故本题应选E.18.设a,b均为正数,则a,b的比例中项为(1)a,b的算术平均值为nA.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.√D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.条件(1)、(2)单独均不充分.当两个条件合在一起时,有化简得a+b=2m,所以选C.19.3x 2一4ax+a 2<0.A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.√E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.不等式3x 2一4ax+a 2<0可化为 (3x一a)(x—a)<0 由条件(1),当a<0,时,有 x一a>0,3x一a<0 可见条件(1)充分.由条件(2),当a>0,时,有 x一a<0,3x一a>0 可见条件(2)充分.故本题应选D.20.x的值,这个分式为一个定值. (1)7a=11b=0 (2)11b=7b=0A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.√C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.显然,x=0使有意义,而.即此定值应为由条件(1),,代入f(x),有可见,条件(1)不充分.由条件(2),,代入f(x),得可见,条件(2)充分.故本题应选B.21.S 6 =126. (1)数列{a n )的通项公式是a n =10(3n+4)(n∈N) (2)数列{a n )的通项公式是a n =2 n (n ∈N)A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.√C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.由条件(1),a 1 =70,而 a n+1一a n =10(3n+3+4)一10(3n+4)=30.所以{a n }是以a 1 =70为首项,d=30为公差的等差数列,于是,故条件(1)不充分.由条件(2),数列{a n }是以首项为a 1 =2,公比为q=2的等比数列,于是所以条件(2)充分.故本题应选B.22.将图中矩形的A,B,C,D,E五个区域用红、黄、绿、蓝、白五种颜色之一着色,使相邻的区域着有不同的颜色,则共有360种着色方式.A.条件(1)充分,但条件(2)不充分.√B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.对于条件(1),依次对图中的五个区域着色,则区域A有5种着色方式,区域B有4种着色方式,区域C有3种着色方式,区域D有2种着色方式,区域E有3种着色方式,所以,共有 5×4×3×2×3=360 种着色方式,条件(1)充分.对于条件(2),类似地分析,可知该矩形各区域的着色方式共有5×4×3×3×3=540 种,故条件(2)不充分.故本题应选A.23.设△ABC的三边为a,b,c,则可判定△ABC为直角三角形. (1)a(1+x 2 )+2bx一c(1一x 2 )=0有两个相等实根 (2)ax 2 +bx+c=0的一个根是另一个根的2倍A.条件(1)充分,但条件(2)不充分.√B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.由条件(1),一元二次方程可化为 (a+c)x 2 +2bx+(a一c)=0 其判别式△=4b 2一4(a+c)(a一c)=0 化简得b 2 =a 2—c 2.即a 2 =b 2 +c 2.可知AABC为直角三角形,条件(1)充分.由条件(2),设该一元二次方程的两根为α,β,且α=2β,则所以,故不能判定AABC为直角三角形,条件(2)不充分.故本题应选A.24.两直线y=x+1,y=ax+7与x一3 (2)a=一2A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.√C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.如图21—3,直线y=x+1与x轴的交点记作A(一1,0).直线y=ax+7与x轴交点记作.解方程组,得两条直线交点两直线与x轴围成区域为△ABC.由条件(1),a=一3,所以两直线交点C的坐标为.而B点坐标为,所以线段AB长为,于是△ABC的面积可见,条件(1)不充分.由条件(2),a=一2,则B点坐标为,线段AB长为,两直线交点C的坐标为(2,3),所以,△ABC的面积故条件(2)充分.故本题应选B.25.(1)事件A,B相互独立,A和B事件A发生且B不发生的概率与事件B发生且A不发生的概率相等A.条件(1)充分,但条件(2)不充分.B.条件(2)充分,但条件(1)不充分.C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.√D.条件(1)充分,条件(2)也充分.E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.条件(1)、(2)单独都不充分.两个条件合在一起时,有又A与B相互独立,所以A与B,A与B,A与B相互独立,所以即可得P(A)=P(B),且故本题应选C.。