耦合电感的等效电路
- 格式:doc
- 大小:1.28 MB
- 文档页数:2

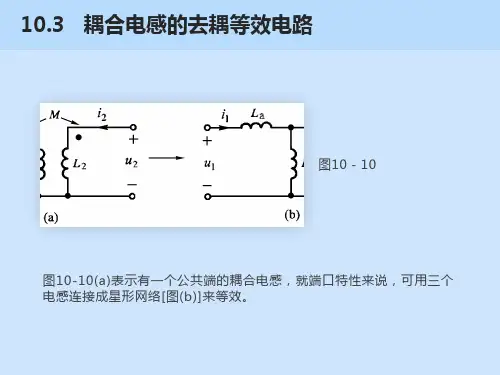
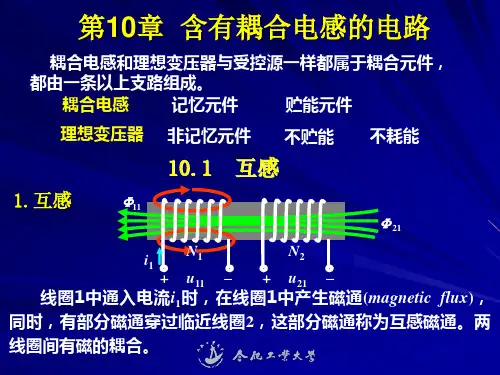

14-2 耦合电感的等效电路
耦合电感的等效电路包括两个不同的电路:主电路和耦合电路。
主电路指的是两个电感器分别与各自的电源相连的电路,而耦合电路则是两个电感器之间通过磁场相互耦合的电路。
主电路的等效电路可以通过简单的串联电路或并联电路来表示。
耦合电路可以表示为一个电感器和一个磁芯之间的电路,其中磁芯通过磁场将电感器之间的电能耦合在一起。
当两个耦合电感器之间有运动时,它们之间的磁场也会随之改变。
这种变化会导致电感器之间的电能转移,从而影响它们的电流和电压。
耦合电感的等效电路可以通过电容器、变压器、晶体管等电子元件来实现。
这些元件可以用于设计各种类型的电路,从而满足不同的需求。
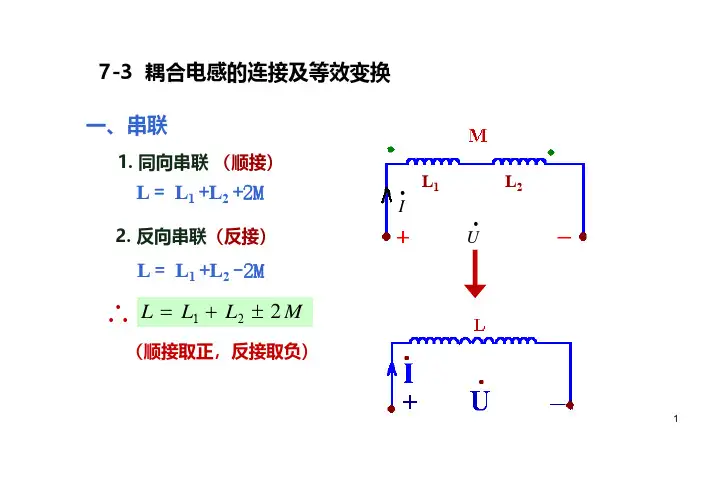


耦合电感并联等效电感公式推导
在电路中,电感是一种用来存储电能的元件,而耦合电感则是指两个或多个电感之间存在一定的磁耦合关系。
当两个电感之间存在磁耦合时,它们的等效电感将会发生变化。
本文将介绍耦合电感并联时的等效电感公式推导过程。
假设有两个耦合电感L1和L2,它们之间存在一定的磁耦合。
当这两个耦合电感并联在一起时,它们的等效电感记为Leq。
根据电路理论,耦合电感并联时的等效电感可以通过以下公式进行推导:
1. 首先,我们可以利用电感的互感系数M来描述两个电感之间的磁耦合关系。
互感系数M的取值范围在0到1之间,当M等于1时,表示两个电感之间完全磁耦合,而当M等于0时,表示两个电感之间没有磁耦合。
2. 根据耦合电感的定义,我们可以得到Leq与L1和L2之间的关系:Leq = L1 + L2 + 2M√(L1L2)。
这个公式表示了当两个耦合电感并联时,它们的等效电感与它们本身的电感值以及互感系数之间的关系。
3. 通过上述公式,我们可以看到,耦合电感并联时的等效电感不仅与两个电感的电感值有关,还与它们之间的磁耦合程度有关。
当M 接近1时,Leq的值将会显著大于L1和L2之和,这是因为磁耦合会增加电感的存储能量。
耦合电感并联时的等效电感公式可以通过电感的互感系数M来描述两个电感之间的磁耦合关系。
通过合理选择互感系数M的取值,我们可以控制并联电路的等效电感值,从而满足电路设计的需求。
通过深入理解耦合电感并联的等效电感公式推导过程,我们可以更好地应用这一原理于实际电路设计中,提高电路性能和稳定性。

端联接在一起,该联接方式称为同向串联(顺接);图6-42( a )中L 1和L 2的同名端连接在l_2 M :u'u 2—(b )L 1 ■ L2 - 2M_____ ■■- __________________________4 U -(c) 图6-41 串联耦合电路的去耦顺接时,支路的电压电流关系为uM 色)(L 2d M di ) dt dt dt dt-J: -J: -J:= (L j M )匕(L 2 M )2 = (L 1L 2 2M )d -dt dtdt根据等效变换的概念,该顺接耦合电感可用一个(L j • M )的电感和一个 (L 2M )的电感相串联的电路等效替代,或用一个(J • L 2• 2M )的电感等效替代。
如图6-41 ( b )所示。
反接时,支路的电压电流关系为八 di R” didi di u =馆 M ) (L 2M ) dt dtdtdt-J:-J:-J:=(L i - M )—— (L 2- M )——=(L iL 2- 2M )—dt dtdtdi根据等效变换的定义, 该反接耦合电感可用一个(L r -M )的电感和一个 (L 2- M )的电感相串联的电路等效替代, 或用一个 (J • L 2-2M )的电感等效替代。
如图6-42 ( b )所示。
6.5.2耦合电感的等效电路 1.耦合电感的去耦等效电路 (1)串联电路去耦图6-41 (a )和图6-42( a )即为耦合电感的串联电路。
图6-41 (a )中J 和L 2的异名起,该连接方式称为反向串联(反接)(a )l_1 ::;U 1+u. M ,L1 一、L2比 _ - u2-L2「MU2 -M亠U1(a)(c )图6-42 串联耦合电路的去耦(2) T 型电路去耦图6-43 ( a )和图6-44 (a )即为耦合电感的T 型连接电路,其中图 6-43 ( a )中耦合电感的联接形式称为同侧联接,图6-44 (a )的联接形式称为异侧联接。


耦合电感电路的等效6种模型
耦合电感电路的等效模型有以下6种:
1. 互感耦合模型:将耦合电感电路分解为两个互感元件(互感电感),通过互感系数来描述电感之间的耦合程度。
2. 理想变压器模型:将耦合电感电路看作是一个理想变压器,将互感耦合转化为变压器变比。
3. T模型:将耦合电感电路通过一根传输线分为两段,在传输线的中心位置连接一个串联电感,表示耦合电感。
4. π模型:将耦合电感电路通过一根传输线分为两段,在传输线的中心位置连接一个并联电感,表示耦合电感。
5. 串联模型:将耦合电感电路看作是一个串联电感,将多个电感元件串联连接。
6. 并联模型:将耦合电感电路看作是一个并联电感,将多个电感元件并联连接。
以上是耦合电感电路的常见等效模型,根据具体情况选择适合的模型进行分析和计算。
记得具体情况具体分析,如果需要更详细的解答,可以提供具体的电路图等信息。
多线圈耦合电感等效概述及解释说明引言是一篇长文的开端,通过简明扼要地介绍文章的主题、结构和目的,帮助读者对接下来的内容有一个整体的把握。
在本篇文章中,引言部分分为三个方面进行阐述:概述、文章结构以及目的。
1.1 概述多线圈耦合电感是电子领域中一个重要且广泛应用的概念。
它是指通过磁场耦合实现电感元件之间能量传输和信号传递的一种技术。
相比于单线圈电感,多线圈耦合电感能够提供更高的电感值,并具备更复杂的工作原理和更广泛的应用领域。
1.2 文章结构本文将分为五个部分进行阐述多线圈耦合电感等效模型及参数计算方法。
首先,在第二部分中,我们将详细介绍多线圈耦合电感的基本概念与原理,包括定义、工作原理以及应用领域。
在第三部分中,我们将探讨多线圈耦合电感等效模型及参数计算方法,主要包括串联和并联多线圈耦合电感等效模型以及参数计算方法,并举例进行实例分析。
接下来,在第四部分,将介绍多线圈耦合电感的设计原则和优化方法,这包括了设计要求以及实现优化的方法和策略,并通过实例验证与性能评估来验证。
最后,在第五部分中,我们将进行总结回顾,概括文章的主要内容,并展望未来研究方向。
1.3 目的本文旨在系统地介绍多线圈耦合电感等效模型及参数计算方法,展示其在电子领域中的重要性和广泛应用。
通过本文的阐述,读者可以对多线圈耦合电感有一个整体而清晰的认识,并了解其设计原则、优化方法以及相关参数计算。
希望本文能够为相关领域工作者提供指导和参考,促进多线圈耦合电感技术的广泛应用和进一步发展。
2. 多线圈耦合电感的基本概念与原理:2.1 多线圈耦合电感的定义:多线圈耦合电感是指由多个线圈相互耦合而形成的电感器件。
它由两个或多个线圈组成,其中有一个主要线圈和其他附属线圈通过磁场相互连接。
这种耦合可以通过将附属线圈绕在主要线圈周围或与主要线圈共享磁芯来实现。
2.2 多线圈耦合电感的工作原理:多线圈耦合电感利用了磁场的作用,当通过主要线圈施加交流电源时,会在主要线圈中产生变化的磁场。
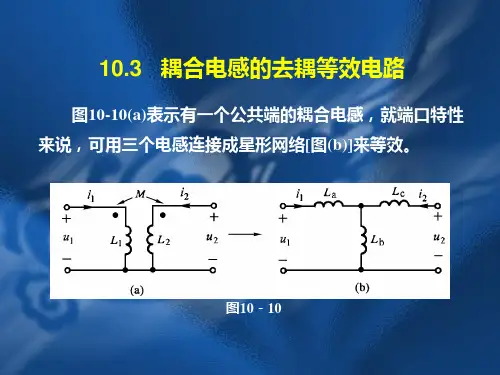
6.5.2 耦合电感的等效电路 1. 耦合电感的去耦等效电路 (1)串联电路去耦
图6-41(a )和图6-42(a )即为耦合电感的串联电路。
图6-41(a )中1L 和2L 的异名端联接在一起,该联接方式称为同向串联(顺接);图6-42(a )中1L 和2L 的同名端连接在一起,该连接方式称为反向串联(反接)。
1
+-
2
u
M L +i
M
L +1
+-
2
u
(a ) (b )
M
L L 2++-
+
u
(c )
图6-41 串联耦合电路的去耦
顺接时,支路的电压电流关系为
dt
di M L L dt di
M L dt
di M L dt di M
dt di L dt di M dt di L u )
2()
()()
()(21212
1
++=+++=+++=
根据等效变换的概念,该顺接耦合电感可用一个)(1M L +的电感和一个)(2M L +的电感相串联的电路等效替代,或用一个)2(21M L L ++的电感等效替代。
如图6-41(b )所示。
反接时,支路的电压电流关系为
dt
di M L L dt di M L dt
di M L dt di M
dt di L dt di M dt di L u )
2()()()
()(21212
1
-+=-+-=-+-=
根据等效变换的定义,该反接耦合电感可用一个)(1M L -的电感和一个)(2M L -的电感相串联的电路等效替代,或用一个)2(21M L L -+的电感等效替代。
如图6-42(b )所示。
1
+-
2
u
M L -i
M
L -1+-
2
u
(a ) (b )
M L L 2-+i
-
+
u
(c )
图6-42 串联耦合电路的去耦
(2)T 型电路去耦
图6-43(a )和图6-44(a )即为耦合电感的T 型连接电路,其中图6-43(a )中耦合电感的联接形式称为同侧联接,图6-44(a )的联接形式称为异侧联接。
T 型电路的等效去耦网络分别如图6-43(b )和图6-44(b )所示(证明从略)。
请特别注意等效变换前后O 点的位置。
(a ) (b )
图6-43 T 型电路的去耦
(a ) (b )
图6-44 T 型电路的去耦
2. 耦合电感的等效受控源电路
耦合电感上的互感电压是可以用电流控电压源CCVS 表示出来的,所以耦合电感的另一种等效电路就是含CCVS 的无互感电路。
图6-45(b )就是图6-45(a )所示的耦合电感的等效受控源电路。
(a ) (b ) 图6-45 耦合电感的等效受控源电路。