5流体力学第五章量纲分析与相似原理5
- 格式:ppt
- 大小:2.16 MB
- 文档页数:47




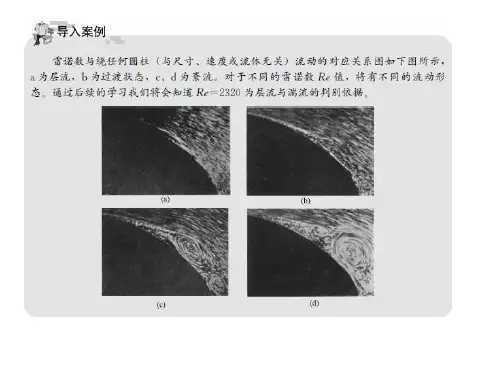
第五章 相似理论与量纲分析实际工程中,由于流体粘性的存在和边界条件的多样性,流动现象极为复杂,往往难以通过解析的方法求解。
此时,不得不依赖实验研究。
通常,实际工程或实物(统称原型)的尺寸太大,直接进行实验会耗费大量的人力和物力,有时甚至难以实现。
因此,大多数实验都是在比原型小的模型上进行的(称为模型实验)。
通过模型实验,得出实验结果,进而预测原型中将要发生的流动现象。
那么怎样才能保证模型与原型有相同的流动规律呢?这就是相似理论要研究的问题。
量纲分析则是在观测流动现象的基础上,建立流动各影响因素的正确关系。
§5.1 相似理论5.1.1 流动相似为了保证模型流动(用下标m 表示)与原型流动(用下标p 表示)具有相同的流动规律,并能通过模型实验结果预测原型流动情况,模型与原型必须满足流动相似,即两个流动在对应时刻对应点上同名物理量具有各自的比例关系,具体地说,流动相似就是要求模型与原型之间满足几何相似、运动相似和动力相似。
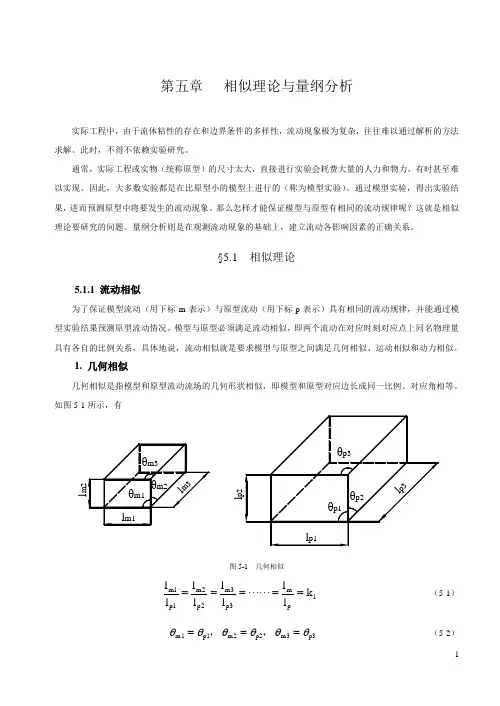
1. 几何相似几何相似是指模型和原型流动流场的几何形状相似,即模型和原型对应边长成同一比例、对应角相等。
如图5-1所示,有图5-1 几何相似l pm 3p 3m 2p 2m 1p 1m k l ll l l l l l ===== (5-1) p3m3p2m2p1m1θθθθθθ===,, (5-2)式中k l 称为长度比尺,则面积比尺2l 2p 2m p m A k l l A A k === (5-3)体积比尺3l 3p3m p m V k l l V V k === (5-4)2. 运动相似运动相似是指模型和原型流动的速度场相似,即两个流动在对应时刻对应点上的速度方向相同,大小成同一比例。
如图5-2所示,有图5-2 运动相似u pm p2m2p1m1k u uu u u u ==== (5-5) 式中k u 称为速度比尺。
由于各对应点速度成同一比例,因此相应断面的平均速度必然有同样的比尺u pmv k v v k ==(5-6) 将t l v=代入上式,得tlm p p m p p m m p m v k k t l t l t l t l v v k ==== (5-7)式中p m tt t k =称为时间比尺。




第五章相似原理与量纲分析对于复杂的实际工程问题,直接应用基本方程求解,在数学上极其困难,因此需有赖于实验研究来解决。
本章主要阐述有关实验研究的基本理论和方法,包括流动相似原理,相似准则,量纲和谐原理及量纲分析方法等。
第一节流动相似原型:天然水流和实际建筑物称为原型。
模型:通常把原型(实物)按一定比例关系缩小(或放大)的代表物,称为模型。
水力学模型试验:是依据相似原理把水工建筑物或其它建筑物的原型按一定比例缩小制成模型,模拟与天然情况相似的水流进行观测和分析研究,然后将模型试验的成果换算和应用到原型中,分析判断原型的情况。
水力学模型试验的目的:利用模型水流来模拟和研究原型水流问题。
关键问题:模型水流和原型水流保持流动相似。
流动相似:两个流动的相应点上的同名物理量(如速度、压强、各种作用力等)具有各自的固定比例关系,则这两个流动就是相似的。
模型和原型保证流动相似,应满足:几何相似运动相似动力相似初始条件和边界条件相似1. 几何相似几何相似:指原型和模型两个流场的几何形状相似,即原型和模型及其流动所有相应的线性变量的比值均相等。
长度比尺:(5-1)面积比尺:2 4 V ?2(5-2)体积比尺:(5-3)2.运动相似运动相似:是指流体运动的速度场相似,也即两流场各相应点(包括边界上各点)的速度度a方向相同,且大小各具有同一比值。
速度比尺:7 —旳—厶仏_ ? ? -1(5-4)加速度比尺: 3_ T _ 旳仏? -2 _ ? 了-13-石-硕_的■以(5-5)u及加速3.动力相似动力相似:是指两流动各相应点上流体质点所受的同名力方向相同,其大小比值相等。
4.初始条件和边界条件的相似初始条件:适用于非恒定流。
边界条件:有几何、运动和动力三个方面的因素。
如固体边界上的法线流速为零,自由液面上的压强为大气压强等。
流动相似的含义:几何相似是运动相似和动力相似的前提与依据;动力相似是决定二个液流运动相似的主导因素;运动相似是几何相似和动力相似的表现;凡流动相似的流动,必是几何相似、运动相似和动力相似的流动。