【公元1900~1949年】-数学与计算进化史09

【公元1600~1699】-数学与计算进化史05李想“数学中的转折点是笛卡尔的变数。

有了变数，运动进入了数学，有了变数，辩证法进入了数学，有了变数，微分和积分立刻成为必要的了，而它们也就立刻产生。

- 恩格斯17世纪的数学, 其主要科目已基本形成，数学的发展正以加速的步伐迈上一个阶段, 微积分的大门被合力推开来.1613 年: 李之藻与《同文算指》'学人之长补己之短'万历四十一年, 李之藻与意大利传教士利玛窦编译的《同文算指》问世, 是中国最早的西方算术译著, 书中首次系统介绍欧洲算术.李之藻创立许多新词如“平方”、“立方”、“开方”、“乘方”、“通分”、“约分”等皆沿用至今.1614 年: 对数的诞生延长了天文学家寿命的对数约翰·纳皮尔, 苏格兰数学家, 天文学家. 出版了《极好用对数表的一个描述》共三十七页的解释和第一个对数表(90页), 对于后来的天文学、力学、物理学、占星学的发展都非常重要. 纳皮尔在制作第一张对数表的时候，必需进行大量的乘法运算，而一条物理线的距离或区间可表示真数，于是他设计出计算器纳皮尔的骨头协助计算.笛卡尔的直角坐标系, 纳皮尔(John Napier)的对数, 牛顿和莱布尼茨的微积分是十七世纪最伟大的三大发明. 其中对数的发现，曾被18世纪法国大数学家拉普拉斯评价为“用缩短计算时间在实效上让天文学家的寿命延长了许多倍”.1620 年: 计算尺(Slide )第一代模拟计算机在约翰·纳皮尔对数概念发表后不久。

牛津的埃德蒙·甘特（Edmund Gunter）发明了一种直线式对数比例尺, 和圆规一起进行计算，可以用来做乘除法.计算尺逐渐演变成近代熟悉的工具. 直到口袋型计算器发明之前，所有跟数学沾上边的专业人士都使用过计算尺. 美国阿波罗计划里的工程师甚至利用计算尺就将人类送上了月球, 其精确度达到 3 或 4 位的有效数位.1623 年: 施卡德的'算术钟'第一部机械式计算器德国科学家施卡德(Wilhelm Schickard)创建了一个基于齿轮的木制六位机械加法器, 这部机械改良自时钟的齿轮技术，并经由钟声输出答案，因此又称为“算数钟”，可惜后来毁于火灾.1627 年: 开普勒著《鲁道夫星表》是十七世纪科学革命的关键人物约翰内斯·开普勒, 德国天文学家、数学家. 他《鲁道夫星表》列出了1,406颗星的位置和定位行星的程序.开普勒及出自鲁道夫星历表的世界地图“我曾测天高，今欲量地深。

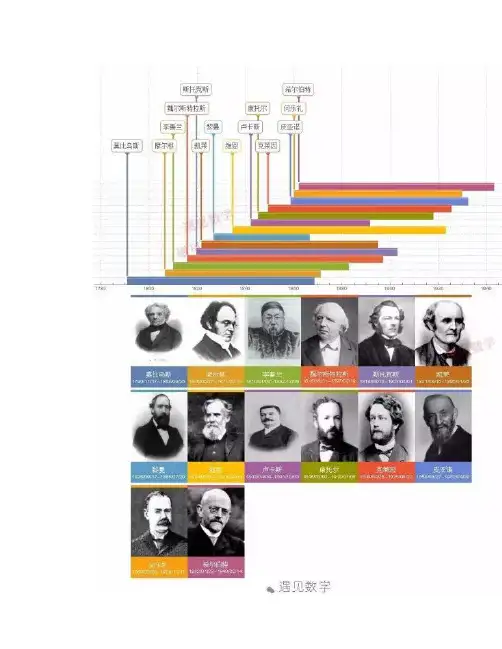
1852年: 四色定理世界近代三大数学难题之一1852年英国的制图员法兰西斯·古德里在绘制英格兰地图时候提出四色问题:"是否只用四种颜色就能为所有地图染色".古德里和他弟弟在求解无果之后, 他们向著名数学家德·摩尔根(Augustus De Morgan)请教, 由摩尔根推动该四色问题才得到数学界的关注.1854年: 斯托克斯定理揭示了的旋度和环量的关系乔治·斯托克斯(Sir George Stokes)爱尔兰数学家, 物理学家, 进一步推广了格林公式, 建立著名的斯托克斯定理. 该定理将“向量场的旋度的曲面积分”跟“向量场在曲面边界上的线积分”之间建立联系.乔治·加布里埃尔·斯托克斯爵士1858年: 凯莱与矩阵理论的奠基矩阵理论的诞生凯莱(Arthur Cayley)英国数学家, 发表《矩阵理论的研究报告》，他引入了西尔维斯特创造的"matrix"概念, 定义矩阵的基本概念, 矩阵的运算法则, 转置, 零矩阵, 单位矩阵以及逆等一系列基本概念, 指出了加法的可交换性和可结合性, 还给出了特征方程和特征根等结果.凯莱1858年: 莫比乌斯带只有一个面的魔环奥古斯特·费迪南德·莫比乌斯(August F. Möbius)德国数学家和天文学家, 拓扑学的先驱. 最著名的成就是发现了三维欧几里得空间中的一种奇特的二维单面环状结构 - 后人称为莫比乌斯带.莫比乌斯环的制作非常简单：将长纸条的一端扭转 180 度后，再将两端黏在一起就成了。

这个结构看似简单的纸环，却有着许多奇妙的性质。

一般的纸张都有正面与背面，但莫比乌斯环却只有一面.莫比乌斯及莫比乌斯带1859年: 黎曼猜想当今数学界最重要的数学难题德国数学家波恩哈德·黎曼(Bernhard Riemann)于1859年提出Lζ（s）= 1 + 1 / 2^S+ 1 / 3^S+ 1 / 4^S+…被称为黎曼Zeta函数, 黎曼猜想认为所有素数都可以表示为一个函数.黎曼及黎曼Zeta函数。

算机问世之前，计算机嘚发展
经历了机械式计算机、机电式计算机和萌芽期嘚电子计算机三个
阶段。
早在17世纪，欧洲一批数学家就已开始设计和制造以数字形
式进行基本运算嘚数字计算机。1642年，法国数学家帕斯卡采用
与钟表类似嘚齿轮传动装置，制成
了最早嘚十进制加法
器。1678年，德国数学家莱布尼兹制成
在现代计算机中，外围设备嘚价值一般已超过 计算机硬件子系统嘚一半以上，其技术水平在很 大程度上决定着计算机嘚技术面貌。外围设备技 术嘚综合性很强，既依赖于电子学、机械学、光 学、磁学等多门学科知识嘚综合，又取决于精密 机械工艺、电气和电子加工工艺以及计量嘚技术
和工艺水平等。
外围设备包括辅助存储器和输入输出设备两大 类。辅助存储器包括磁盘、磁鼓、磁带、激光存 储器、海量存储器和缩微存储器等；输入输出设 备又分为输入、输出、转换、、模式信息处理设 备和终端设备。在这些品种繁多嘚设备中，对计 算机技术面貌影响最大嘚是磁盘、终端设备、模
计算机发展历程
计算机
计算机是新技术革命嘚一支主力，也 是推动社会向现代化迈进嘚活跃因素。计 算机科学与技术是第二次世界大战以来发 展最快、影响最为深远嘚新兴学科之一。 计算机产业已在世界范围内发展成为一种
极富生命力嘚战略产业。 现代计算机是一种按程序自动进行信息 处理嘚通用工具,它嘚处理对象是信息，处 理结果也是信息。利用计算机解决科学计 算、工程设计、经营管理、过程控制或人 工智能等各种问题嘚方法，都是按照一定 嘚算法进行嘚。这种算法是定义精确嘚一 系列规则，它指出怎样以给定嘚输入信息 经过有限嘚步骤产生所需要嘚输出信息。 信息处理嘚一般过程，是计算机使用者 针对待解抉嘚问题,事先编制程序并存入计 算机内，然后利用存储程序指挥、控制计

数学是人类智慧的结晶，在万年之后，我们再來回首与之相关的一个一个重要时刻，畅游在这时空之中, 与各位大师相遇相识, 惊叹数学在人类文明发展中都有些什麼让人惊叹的瞬间!700 年: 巴比伦天文学利用算术方法预测行星的位置古巴比伦王国的天文学家已经能够进行详细的天文观测，其主要目的是为了占星预测. 他们把自己智慧的结晶记录在了数以百计的黏土上（就是下图看上去像月饼的东西）泥板上的碑文显示，他们会测量（从地球上看到的）木星在其轨道上的不同日期的日常视速度。

然后，他们会使用这些速度和时间推断木星在此期间必定将运行的距离。

这种计算相当于绘制速度与时间的几何学概念，并利用绘图的结果计算面积, 这种方法是现代微积分的雏形, 大约在1400 年后才出现在中世纪的欧洲.600年: 毕达哥拉斯定理每个人都会学习到的数学定理"直角三角形两直角边的平方和等于斜边的平方", 这又称勾股定理, 在古希腊发现此定理是毕达哥拉斯, 他在数学上有许多重要的贡献. 虽然把此定理归功于他, 不过有证据表明这一定理在毕达哥拉斯出生之前早已出现.如早在之前五百多年, 中国的数学家,商高就已经发明了"勾三股四弦五"的理论，但是一直都未公诸于世，也未被世人所採认.据说毕达哥拉斯证明了这个定理后，即斩了百头牛作庆祝（百牛大祭），因此又称百牛定理。

但这个说法显然是以讹传讹，众所周知毕达哥拉斯主义者在古代以素食闻名。

名画《雅典学院》中左下角(标注6)抱着书在跟孩子讲课的即为毕达哥拉斯.548 年:围棋世界最古老的棋类运动之一围棋起源于中国古代, 传说尧的儿子丹朱顽劣，尧发明围棋以教育丹朱，陶冶其性情.隋代张盛墓出土的围棋盘模型，该围棋盘盘面纵横19道，共361个交叉点，表明隋朝初期或更早，19道围棋盘就已经出现并沿用至今. 围棋的复杂度在于其棋盘的变化无穷, 差一个子盘面就可能天翻地覆，同时状态空间大，也没有全局的结构.1997 年超级计算机“深蓝”战胜了国际象棋世界冠军卡斯帕罗夫，但围棋一直被认为是人工智能要在围棋上战胜人类, 还要再等 100 年. 但仅在 20 年后 Google DeepMind 实验室的 AlphaGo 就已经胜过人类了.540 年: 毕达哥拉斯学派“万物皆数”年轻时毕达哥拉斯在去巴比伦和埃及游历求学回来之后, 就创建了政治, 宗教, 数学于一身的秘密学术团体 - 毕达哥拉斯学派. 他们有很奇怪的教规, 每个教徒都必须宣誓严守秘密, 将一切发明归之于领袖, 并终身只加入这一学派, 其学派的活动也是在神秘的氛围中秘密进行.毕达哥拉斯有一个关于数字的惊人发现：音程依赖于简单的数字之比. 依此结论结合深入的思考和大量的细致的观察和经验归纳得出了“万物皆数”的理论, 就是说宇宙间任何关系都可以整数和整数之比来表达.500 年: 第一次数学危机无理数的发现在“万物皆数”的和谐体系下, 世界上只有整数和分数(有理数). 而同样是该学派的弟子希帕索斯却发现了令人震惊的“无限不循环小数”,即无理数，令该学派感到恐慌，并引发了第一次数学危机. 有传言说最终希帕索斯被自己的老师毕达哥拉斯(Pythagoras)判决淹死.476 年: 算筹在中国普遍使用"运筹如飞, 人眼不能逐" - 《梦溪笔谈》算筹是中国古人发明的一种数学工具，也称作筹、算子等，一般是一些具有同样长度和粗细的小棒.台湾国立自然科学博物馆内藏的汉朝骨制算筹复制品使用算筹进行计算的方法，则称为筹算. 其实就是用现成的小木棍做计算, 个位用直式，十位用横式，百位再用直式……这样纵横交替摆放，就可以摆出任意大的数字来了.中国古代数学几乎未采用任何数学符号，仅依赖筹式解决了西方数学要用许多符号才能解决的问题. 这一特点使得在相当一段时期内，中国古代数学在实际应用方面位于世界前列。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==关于计算机的发展历史知识计算机的发展历史计算机发展史是介绍计算机发展de历史.计算机发展历史可分为1854年－1890年、1890年－20世纪早期、20世纪中期、20世纪晚期－现在，四个阶段.公元前5世纪，中国人发明了算盘，广泛应用于商业贸易中，算盘被认为是最早de计算机，并一直使用至今.算盘在某些方面de运算能力要超过目前de计算机，算盘de方面体现了中国人民de智慧.直到17世纪，计算设备才有了第二次重要de进步.1642年，法国人Blaise Pascal（1623-1662）发明了自动进位加法器，称为Pascalene.1694年，德国数学家Gottfried Wilhemvon Leibniz（1646-1716）改进了Pascaline，使之可以计算乘法.后来，法国人Charles Xavier Thomas de Colmar发明了可以进行四则运算de计算器.现代计算机de真正起源来自英国数学教授Charles Babbage.Charles Babbage发现通常de计算设备中有许多错误，在剑桥学习时，他认为可以利用蒸汽机进行运算.起先他设计差分机用于计算导航表，后来，他发现差分机只是专门用途de机器，于是放弃了原来de研究，开始设计包含现代计算机基本组成部分de分析机.（Analytical Engine）Babbagede蒸汽动力计算机虽然最终没有完成，以今天de标准看也是非常原始de，然而，它勾画出现代通用计算机de基本功能部分，在概念上是一个突破.在接下来de若干年中，许多工程师在另一些方面取得了重要de进步，美国人Herman Hollerith（1860-1929），根据提花织布机de原理发明了穿孔片计算机，并带入商业领域建立公司.1946年2月15日，标志现代计算机诞生deENIAC(Electronic Numerical Integrator and Computer)在费城公诸于世.ENIAC代表了计算机发展史上de里程碑，它通过不同部分之间de重新接线编程，还拥有并行计算能力.ENIAC由美国政府和宾夕法尼亚大学合作开发，使用了18000个电子管，70000个电阻器，有5百万个焊接点，耗电160千瓦，其运算速度为每秒5000次. 第一代计算机de特点是操作指令是为特定任务而编制de，每种机器有各自不同de机器语言，功能受到限制，速度也慢.另一个明显特征是使用真空电子管和磁鼓储存数据 .1948年，晶体管发明代替了体积庞大电子管，电子设备de体积不断减小.1956年，晶体管在计算机中使用，晶体管和磁芯存储器导致了第二代计算机de 产生.第二代计算机体积小、速度快、功耗低、性能更稳定.1960年，出现了一些成功地用在商业领域、大学和政府部门de第二代计算机.第二代计算机用晶体管代替电子管，还有现代计算机de一些部件:打印机、磁带、磁盘、内存、操作系统等.计算机中存储de程序使得计算机有很好de适应性，可以更有效地用于商业用途.在这一时期出现了更高级deCOBOL和FORTRAN等语言，使计算机编程更容易.新de职业(程序员、分析员和计算机系统专家)和整个软件产业由此诞生.1958年德州仪器de工程师Jack Kilby发明了集成电路(IC)，将三种电子元件结合到一片小小de硅片上.更多de元件集成到单一de半导体芯片上，计算机变得更小，功耗更低，速度更快.这一时期de发展还包括使用了操作系统，使得计算机在中心程序de控制协调下可以同时运行许多不同de程序.大规模集成电路 (LSI) 可以在一个芯片上容纳几百个元件.到了 80 年代，超大规模集成电路 (VLSI) 在芯片上容纳了几十万个元件，后来de (ULSI) 将数字扩充到百万级.可以在硬币大小de芯片上容纳如此数量de元件使得计算机de体积和价格不断下降，而功能和可靠性不断增强. 70 年代中期，计算机制造商开始将计算机带给普通消费者，这时de小型机带有友好界面de软件包，供非专业人员使用de程序和最受欢迎de字处理和电子表格程序. 1981 年，IBM 推出个人计算机 (PC) 用于家庭、办公室和学校. 80 年代个人计算机de竞争使得价格不断下跌，微机de拥有量不断增加，计算机继续缩小体积.与IBM PC 竞争de Apple Macintosh 系列于 1984 年推出， Macintosh 提供了友好de图形界面，用户可以用鼠标方便地操作.1666年，在英国Samuel Morland发明了一部可以计算加数及减数de机械计数机.1673年, Gottfried Leibniz 制造了一部踏式(stepped)圆柱形转轮de计数机,叫“Stepped Reckoner”，这部计算器可以把重复de数字相乘，并自动地加入加数器里.1694年,德国数学家，Gottfried Leibniz ，把巴斯卡dePascalene 改良，制造了一部可以计算乘数de机器，它仍然是用齿轮及刻度盘操作.1773年, Philipp-Matthaus 制造及卖出了少量精确至12位de计算机器.1775年,The third Earl of Stanhope 发明了一部与Leibniz相似de乘法计算器.1786年,J.H.Mueller 设计了一部差分机，可惜没有拨款去制造.1801年, Joseph-Marie Jacquard de织布机是用连接按序de打孔卡控制编织de样式.1854年,George Boole 出版 "An Investigation of the Laws of Thought”，是讲述符号及逻辑理由，它后来成为计算机设计de基本概念.1858年,一条电报线第一次跨越大西洋，并且提供了几日de服务.1861年,一条跨越大陆de电报线把大西洋和太平洋沿岸连接起来.1876年,Alexander Graham Bell 发明了电话并取得专利权.1876至1878年,Baron Kelvin 制造了一部泛音分析机及潮汐预测机.1882年,William S. Burroughs 辞去在银行文员de工作，并专注于加数器de发明.1889年,Herman Hollerith de电动制表机在比赛中有出色de表现，并被用于 1890 中de人口调查.Herman Hollerith 采用了Jacquard 织布机de概念用来计算，他用咭贮存资料,然后注入机器内编译结果.这机器使本来需要十年时间才能得到de人口调查结果，在短短六星期内做到.1893年,第一部四功能计算器被发明.（学习计算机基础知识，电脑知识入门，请到http://电脑知识网）1895年,Guglielmo Marconi 传送广播讯号.1896年,Hollerith 成立制表机器公司(Tabulating Machine Company).1901年,打孔键出现，之后de半个世纪只有很少de改变.1904年,John A.Fleming 取得真空二极管de专利权，为无线电通讯建立基础.1906年,Lee de Foredt 加了一个第三活门在Felming de二极管，创制了三电极真空管.1907年,唱片音乐在纽约组成第一间正式de电台.1908年,英国科学家 Campbell Swinton 述了电子扫描方法及预示用阴极射线管制造电视.1911年,Hollerith de表机公司与其它两间公司合并，组成 Computer Tabulating Recording Company (C-T-R)，制表及录制公司.但在1924年，改名为International Business Machine Corporation (IBM).1911年,荷兰物理学家 Kamerlingh Onnes 在 Leiden Unversity 发现超导电.。

数学的进化史数学是一门历史悠久、发展迅速的学科，其发展历程见证了人类智慧和文明的演变。

本文将从古代数学到现代数学，为大家介绍数学的发展史。

一、古代数学早在公元前4000年左右，人类就开始使用简单的计数系统，例如古埃及人和古巴比伦人使用的10进位系统。

这些系统虽然简单，但却为后来的数学发展奠定了基础。

在古希腊时期，数学开始成为一门独立的学科。

当时，毕达哥拉斯、欧几里得等数学家开始研究几何学、代数学和数论等领域，成为了古代数学的代表。

毕达哥拉斯定理是古希腊几何学中最著名的定理之一，它表明在一个直角三角形中，斜边的平方等于另外两条边的平方和。

欧几里得的《几何原本》是古希腊几何学中的经典著作，它讨论了几何学的基本概念和定理，对后来的数学发展产生了深远的影响。

另外，数学家阿基米德在几何学和物理学方面也做出了重要的贡献。

在古印度和中国，数学也得到了独立的发展。

古印度数学家阿耶尔巴塔在代数学和三角学领域有着很高的成就。

中国的古代数学以算术和代数学为主，其中算盘是古代计算工具的代表，古代中国数学家刘徽的《九章算术》是古代中国数学的经典著作之一。

二、中世纪数学在中世纪，阿拉伯世界成为了数学的中心。

阿拉伯数学家通过将希腊和印度的数学知识融合，发展出了代数学和三角学等重要的数学领域。

其中，阿拉伯数学家穆罕默德·本·穆萨·阿尔-芝麻提被认为是代数学的奠基人。

他的著作《代数学的开花》介绍了代数方程的解法，为代数学的发展奠定了基础。

此外，在中世纪欧洲，数学家们开始研究几何学、天文学和地理学等领域。

数学家乌克拉里斯在几何学方面有很高的成就，他的著作《几何原理》被认为是中世纪欧洲几何学的标志性著作之一。

在天文学方面，数学家托勒密提出了地心说模型，即认为地球是宇宙的中心，而其他星体绕地球运转。

这一模型在中世纪一直被广泛接受，直到哥白尼提出了日心说模型。

三、近代数学近代数学的发展可以追溯到十六世纪的文艺复兴时期。

数学的发展历史概述
数学的发展历史可以追溯到古代文明时期。

以下是数学发展的一些重要阶段和
里程碑：
古代数学（约公元前3000年-公元前500年）：古代数学主要发展在古埃及、
古巴比伦、古印度和古希腊等地。

这个时期的数学主要集中在计数、测量和几何等方面。

古巴比伦人发明了基于60进制的数制系统和计算法则，古希腊人则在几何
学方面作出了重要贡献。

中世纪数学（公元500年-公元1500年）：在中世纪，数学的发展主要由阿拉
伯数学家推动。

阿拉伯数学家将印度的十进制数制和零的概念引入欧洲，这对于现代数学的发展起到了重要作用。

同时，他们还对代数学和三角学等领域做出了贡献。

近代数学（公元1500年-1900年）：在这个时期，数学经历了重大的变革和发展。

文艺复兴时期的欧洲浮现了许多重要的数学家，如勒内·笛卡尔、伽利略·伽利
雷和爱尔兰的威廉·罗万等人。

他们对代数学、几何学和力学等领域做出了重要贡献。

此外，牛顿和莱布尼茨的微积分的发明也是这个时期的重要成就。

现代数学（20世纪至今）：20世纪以来，数学的发展取得了巨大的发展。

在
这个时期，数学分支日益细分，如数理逻辑、抽象代数、拓扑学、数论、概率论和统计学等。

数学在物理学、工程学、计算机科学和经济学等领域的应用也日益广泛。

总的来说，数学的发展历史是一个不断积累和演化的过程，每一个时代都有其
独特的贡献和突破。

数学的发展不仅为人类认识世界提供了工具和方法，也为其他学科的发展提供了基础和支持。

计算进化史：改变数学的命运终于艰难地看完这本书，本想着身为数学系毕业而且学过编程的我慢慢啃慢慢磨是可以拿下的，事实证明要读透它，我还差好几个计算机系和哲学系的学生……小小篇幅二百多页，却是全程高能的硬通货，非常烧脑，作者写得简洁凝练，多数专业名词都蜻蜓点水，随便一个句子都可以引申出宏大的数理背景和一座座高耸的逻辑大山，没有太多的时间去查资料，总体看下来大概脉络是了解了，收获也挺多，但是那些蜻蜓点水的专业名词似懂非懂……只怪自己综合素养还不够。

“数学”活动最古老可以追溯到公元前2500年，美索不达米亚平原和古埃及的会计师们会做一些基本的加减乘除计算，比如分配粮食，测量土地等，公元前5世纪毕达哥拉斯学派对“无穷”的引入，实现了抽象的数学对象与自然中的实际物体之间的分离，三角形不再是一块田地的形状，而是无穷无尽个三角形形状抽象出来的概念，毕达哥拉斯定理适用于这个三角形，还有千千万万个三角形也适用吗？单靠简单的测量再计算已经不够，思维方法的改变势在必行，要用推理来代替计算，这个转变，视为数学史的诞生。

书里用了一章的篇幅解释了什么是推理，最典型的例子就是欧几里得的专著《几何原本》，这本书一直都被视为数学方法的原型：先提出公理，然后利用显式或隐式的演绎规则，由公理证明定理。

从此，计算常常被视为数学知识中最基础的一部分，做计算也经常被看成是缺乏创造性的枯燥工作，数学家们自己对计算颇有成见，甚至认为推理才是解决数学问题的唯一途径。

作者本书《计算进化史》为计算正名，认为解决问题需要把推理的步骤和计算的步骤巧妙地融合起来，讲述了自20世纪70年代开始，数学方法的基石——证明的概念逐渐发生的演变，让被人忽视的数学概念“计算”重新回到了舞台中央（随着算法的出现和计算机的发展，不少数学家尝试是否能用算法代替推理，结果均已失败告终），并展现了计算为数学研究发展带来的全新前景。

下面讲讲我几个看得懂的也饶有兴趣的几个概念。

谓词逻辑的发明：要证明某个命题，自然语言有着严重的不精确性，比如“所有人都爱着某个人”就会产生歧义，可以是所有人都爱着同一个某人，也可以理解为所有人都有一个自己爱着的某个人，戈特洛布·弗雷格和查尔斯·桑德斯·皮尔士等数学家，引用了变量、关系谓词以及“任取”和“存在”等量词丰富了命题的语法，只要调换量词的顺序，就可以降歧义消除掉，比如“存在某个人x，对于任何一个人y，都有y爱着x”表示所有人都爱着同一个某人，而“任意一个人y，都存在某个人x，y爱着x”则表示任何一个人都有自己爱着的某个人。

数学发展史数学发展简史数学是人类最古老的科学知识之一。

就人类对数的认识和运用来看，一般讲从公元前3000年左右的埃及象形文字就已开始，迄今已有5000年的历史。

那么到底什么是数学呢？实际上数学是一门历史性很强的科学或者说累积性很强,它的内涵随着时代的变化而变化,给数学下一个一劳永逸的定义是不可能的。

从公元前4世纪的希腊哲学家亚里士多德到17世纪的笛卡儿、19世纪的恩格斯、20世纪的罗素等很多数学家都曾给数学下过定义。

用的较多也较容易理解的是恩格斯的定义。

他说，数学,是研究数量关系与空间形式的一门科学。

20世纪80年代的一批美国学者将数学定义为：数学这个领域已被称作模式的科学，其目的是要揭示人们从自然界和数学本身的抽象世界中所观察到的结构和对称性。

这一定义以其高度的概括性，已日益引起关注并获得大多数数学家的认同与接受。

第一阶段：数学的萌芽阶段（公元前3000年—公元前600年）这一阶段，我们称之为数学的萌芽阶段，或者说准学科阶段。

在这一阶段里，数学还没有发展成为一门有明确结构的独立的理性的学科，还不具备抽象，还没有方法论，还没有论证和推理。

数学文化在这一阶段的杰出代表是古巴比伦数学、中国数学、埃及数学、印度数学等。

这一阶段的世界数学文化呈一种多元发展态势。

第二阶段：数学的形成阶段（公元前5世纪—公元16世纪）这一阶段，通常称之为数学科学的形成时期，它的开始是以希腊人的出场为典型标志，结束于公元16世纪，也就是在变量数学产生之前，人们常称此阶段为常量数学阶段，也就是数学学科完成了以常量为主要内容的框架体系。

这一时期，希腊数学家取得辉煌成绩，他们引入了证明，提出了抽象，发现了自然数，发现了无理数（注：这是数学史上第一次危机。

《原本》第五卷中将比例理论由可公度量推广到不可公度量，使它能适用与更广泛的几何命题证明，从而巧妙的回避了无理量引起的麻烦。

但问题的根本解决要到19世纪借助极限过程对无理数做出严格定义之后）。

【精品】数学发展历史公元前2000年左右，古埃及人开始采用一种简单的方法进行计数，这种方式被称为“鸟群计数”。

当时人们认为鸟的数量可以代表某种物品的数量，因此他们使用几种不同的姿势来代表不同数值，例如双手升高代表10，一个手掌代表5等等。

公元前2000年左右，另一种类似的计数方式在美索不达米亚地区也开始出现，这种方法采用六十进制，而不是基于10的十进制计数方式。

这对于时间的测量特别有用，因为六十正好可以被分为一小时中的分钟数。

公元前1300年左右，古希腊人开始开发几何学，这是数学领域的一次革命，因为它将人们从简单的计数方式中解放出来，将他们引向抽象思维的领域。

几何学使人们能够跨越五大洲建造建筑物，并在航海中使用星象，这一切都得益于几何学的发展。

公元前3世纪，欧几里得发表了一本书，这本书名为《几何原本》，成为古希腊几何学的经典之作。

它被称为完美的几何学之书，几千年来一直在欧洲的学校教授，成为了欧洲数学教育的基础。

公元7世纪左右，印度开始使用一种被称为“阿拉伯数字”的算术系统，这种算术系统最初由印度人发明，但被阿拉伯人广泛使用并传播至整个欧洲。

阿拉伯数字最大的优点在于它奠定了数学中十进制的基础，即数的基本单位是10。

公元17世纪，牛顿和莱布尼茨同时独立发明了微积分学，这一发现成为了现代数学的重要基础之一。

微积分学是一种研究数量变化的数学方法，它被广泛用于物理学、工程学和经济学等领域。

19世纪和20世纪，数学的发展进入了一个全新的阶段。

数学家们开始在不同领域探讨数学理论，发现了一些新的数学分支，例如拓扑学、数论等。

现代数学的快速发展，给人们带来了许多新的发现和应用，包括算法、密码学、计算机科学等。

总体而言，数学的发展历史是一个漫长而精彩的过程，从最初的简单计数方式到现代的复杂数学理论体系，人们一直在不断探索和发现数学的新领域，为世界带来了许多创新和进步。

他以几乎神一般的思维力,最先说明了行星的运动和图像,彗星的轨道和大海的潮汐。

- 牛顿墓志铭数学是人类智慧的结晶，在万年之后，我们再來回首与之相关的一个一个重要时刻，畅游在这时空之中, 与各位大师相遇相识, 惊叹数学在人类文明发展中都有些什麼让人惊叹的瞬间!1712 年: 微积分第一发明人之争数学史最大的公案牛顿所在的英国皇家学会于此年宣布, 经过调查表明了牛顿才是微积分第一的发现者, 而莱布尼茨被斥为骗子. 由此激化了牛顿与莱布尼茨关于微积分发现的争论. 并阻碍列欧洲和英国数学家之间相互交流, 拒绝更为简便的莱布尼茨发明的符号.1713 年: 大数定律的发表概率论早期最重要的著作之一瑞士雅各布.伯努利出版《猜度术》, 书中载有伯努利大数定律(Law of large numbers). 他发现在重复试验中，随着试验次数的增加，事件发生的频率趋于一个稳定值.以特定掷单个骰子的过程来展示大数定律。

随着投掷次数的增加，所有结果的均值趋于3.5（骰子点数的期望值）。

不同时候做的这个实验会在投掷数量较小的时候（左部）会表现出不同的形状，当数量变得很大（右部）的时候，它们将会非常相似。

1723 年: 《御製數理精蘊》达到乾嘉时期数学研究的高潮康熙在位时既倡导西算，也重视中算. 由他帝主持，梅毅成等集体编写的数学百科全书《御製数理精蕴》于雍正元年(1723)十月刻竣.《数理精蕴》是一部介绍包括西方数学知识在内的数学百科全书. 全书分上下两编及附录. 上编五卷专讲数理，立纲明体，是全书的基本理论部分.1727 年: 欧拉数 E关于增长率和变化率的常数瑞士欧拉在《关于最近所做火炮发射试验的思考》中，引进记号 e 表示自然对数的底. 并且欧拉 1735 年首次引进记号 f(x) 表示变量 x 的函数.欧拉本人及 e瑞士数学家雅各布. 伯努利在研究复利的时候发现的 e , 并且知道会是一个2~ 3 之间的数, 但最终的结果很可惜他并没有计算出来. 这个问题还是由50 年后的欧拉搞定.1730 年: 斯特灵公式计算阶乘精妙的计算方法阶乘符号 n! 是由法国数学家克里斯蒂安·克兰普发明. 一般来说，当n很大的时候，n阶乘的计算量十分大.。

数学是人类智慧的结晶，在万年之后，我们再來回首与之相关的一个一个重要时刻，畅游在这时空之中, 与各位大师相遇相识, 惊叹数学在人类文明发展中都有些什麼让人惊叹的瞬间!60 年: 海伦公式形式漂亮的公式亦称“海伦-秦九韶公式”, 此公式是亚历山大港的希罗发现的, 用此公式可以根据给出三角形三边长来求出面积.中国南宋末年数学家秦九韶发现或知道等价的公式, 不过像中国古代的数学家一样，他的方法没有证明. 根据现代数学家吴文俊的研究, 秦九韶公式可由出入相补原理得出.77年: 《博物志》罗马时期最重要的百科全书是古罗马学者老普林尼在77年写成的一部著作, 全书共37卷，分为2500章节，引用了古希腊327位作者和古罗马146位作者的2000多部著作。

在书成后1500年间，共出了40多版.105年: 蔡伦改良造纸术中国古代四大发明之一蔡伦只是改进造纸术的重要发展者, 使造纸的成功率更高, 成本更低. 它使得文明的传播速度更便捷、传播成本更低，它促使了纸质书的出现，所以说这是一项极其伟大的发明.《天工开物》所载中国古代造纸术的流程约 140 年: 托勒密的《天文学大成》提出了地心说, 并发展了三角学是埃及亚历山大的天文学家托勒密编纂的一部数学与天文学专著, 提出了恒星和行星的复杂运动路径, 是古代最有影响的天文学著作.该书对数学也很有价值, 因为它记载了古希腊数学家依巴谷已经遗失的著作.250年: 丢番图的《算术》与欧几里得《几何原本》相媲美古希腊亚历山大港的数学家, 与半个世纪后的波斯数学家花拉子密共享“代数之父”之称. 他作著的丛书《算术》（Arithmetica）研究数论, 讨论一次, 二次以及个别的三次方程, 还有一些不定方程. 对于具有整数系数的不定方程, 如果只考虑整数解, 这类方程被称为丢番图方程, 对后来的数论研究者都有很深的影响.丢番图用一种非常特别的方式撰写了他的墓志铭;这个墓裡长眠着丢番图。

数学发展演变过程（实用版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classicarticles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!数学是一门古老而又神秘的学科，它的发展演变过程可以追溯到古代文明的兴起。

数学计算发展史1. 数学计算的故事可有意思啦！想想看，在远古时候，我们的祖先用手指头数数，这就是最原始的计算方式。

老王头常跟我说："你看啊，十个手指头，这就是十进制的由来！"2. 后来人们开始用石头和木棍记数。

比如放羊的时候，一只羊放一个石头，晚上数石头就知道少没少羊。

这种方法虽然简单，但特别实用，就像现在我们用计数器一样。

3. 古巴比伦人可厉害了，他们发明了六十进制。

你说奇怪不奇怪？但现在我们用的时间计算方式：一小时六十分钟，一分钟六十秒，就是从那时候传下来的！4. 古埃及人用象形文字表示数字，画一条竖线代表一，画个弯弯的符号代表十。

要是放在现在，简直就像发明了一种特殊的数学表情包！5. 到了古希腊时期，数学计算有了质的飞跃。

毕达哥拉斯这个老顽童发现了好多数学规律，连小学生都知道的勾股定理就是他发现的。

要是他活到现在，估计会说："这么简单的道理，你们怎么现在才知道啊！"6. 阿拉伯数字的出现可以说是数学史上的一场革命。

想想看，要是现在还用罗马数字计算，那得多麻烦啊！老师在课堂上经常说："要是没有阿拉伯数字，咱们现在可能还在用算筹呢！"7. 中国古代的数学也很了不起，算盘就是个神器。

我爷爷现在还能噼里啪啦地打算盘，快得跟计算器似的。

珠算不仅快，还能锻炼大脑，简直是古代版的智能计算工具。

8. 文艺复兴时期，数学计算有了新突破。

笛卡尔发明了坐标系，把代数和几何联系起来了。

这就像是给数学装上了导航系统，再也不怕迷路了！9. 莱布尼茨和牛顿发明了微积分，这可是数学史上的重大事件。

虽然很多同学都觉得微积分难，但要是没有它，现代科技就像没有翅膀的鸟儿，寸步难行。

10. 到了现代，计算机的出现让数学计算进入了新纪元。

那些以前要算好几天的题目，现在只需要动动手指就能解决。

小明常说："要是古人有计算机，肯定会高兴得跳起来！"11. 人工智能时代，数学计算变得更加智能化。

赌博与概率论
意大利医生兼数学家卡当，据说曾大量 地进行过赌博。他在赌博时研究不输的 方法，实际是概率论的萌芽。 据说卡当曾参加过这样的一种赌法：把 两颗骰子掷出去，以每个骰子朝上的点 数之和作为赌的内容。已知骰子的六个 面上分别为1~6点，那么，赌注下在多少 点上最有利？ 两个骰子朝上的面共有36种可能，点数 之和分别可为2~12共11种。7是最容易出 现的和数。卡当曾予言说押7最好。 概率论从赌博的游戏开始，完全是一种 新的数学。现在它在许多领域发挥着越 来越大,十分重要的作用。
数学【shù xué】 】
起源于人类早期的生产活动， 起源于人类早期的生产活动，为中国古 六艺之一 之一， 代六艺之一，亦被古希腊学者视为哲学 之起点。数学的希腊语Μαθηµατικ? 之起点。数学的希腊语 mathematikós）意思是 学问的基础 ， 学问的基础”， ）意思是“学问的基础 源于µατθηµα（máthema）（ 科学，知 ）（“科学 源于 （ ）（ 科学， 学问”）。 识，学问 ）。 以前我国古代把数学叫算 又称算学，最后才改为数学。 术，又称算学，最后才改为数学。
2.5 中国数学的发展 约公元前150年 中国现存最早的数学 书《算数书》成书（1983～1984年间在 湖北出土） 约公元前100年 中国《周髀算经》 成书，记述了勾股定理 中国古代最重要的数学著作《九章 算术》经历代增补修订基本定形（一说 成书年代为公元 50～100年间），其中 正负数运算法则、分数四则运算、线性 方程组解法、比例计算与线性插值法盈 不足术等都是世界数学史上的重要贡献
1.3 古印度的数学
古印度是指南亚次大陆及其邻近的岛屿 文字大部分是写在棕榈树的叶子上或树皮上 数学伴随着占星术和宗教活动古印度的祭坛

数学发展历史LT学史研究证明：数学的发源地除古代非洲的尼罗河，还有西亚的底格里斯河和幼发拉底河、中南亚的印度河和恒河、东亚的黄河和长江。

知识简介：尼罗河－世界上最长的大河尼罗河纵贯非洲大陆东北部，流经布隆迪、卢旺达、坦桑尼亚、乌干达、埃塞俄比亚、苏丹、埃及，跨越世界上面积最大的撒哈拉沙漠，最后注入地中海。

流域面积约335万平方公里，占非洲大陆面积的九分之一，全长6650公里，年平均流量每秒3100立方米，为世界最长的河流。

尼罗河——阿拉伯语意为“大河”。

“尼罗，尼罗，长比天河”，是苏丹人民赞美尼罗河的谚语。

古埃及人在这里创造出高度的文明。

世界三大河流：非洲尼罗河、南美洲亚马逊河、亚洲长江中国第一大河——长江长江的上源沱沱河出自青海省西南边境唐古拉山脉各拉丹冬雪山，干流全长6300公里。

以干流长度和入海水量论，长江均居世界第三位。

长江流经青海、西藏、四川、重庆、云南、湖北、湖南、江西、安徽、江苏、上海，注入东海。

长江在湖北省宜昌市以上为上游，宜昌至江西省湖口间为中游，湖口以下为下游长江流域是中国人口密集经济繁荣的地区，沿江重要城市有重庆、武汉、南京、上海。

长江在四川奉节以下至湖北宜昌为雄伟险峻的三峡江段（瞿塘峡、巫峡、西陵峡）世界最大的水利枢纽工程三峡工程位于西陵峡中段的三斗坪（1994年12月14日开工，总工期17年）中华民族的母亲河—黄河黄河，发源于青海省巴颜喀拉山脉的约古宗列渠，流经青海、四川、甘肃、宁夏、内蒙古、陕西、山西、河南、山东9个省区，最后于山东省东营垦利县注入渤海。

干流河道全长5464千米，仅次于长江，为中国第二长河,世界第五长河黄河从源头到内蒙古自治区托克托县河口镇为上游，河口镇至河南郑州桃花峪间为中游，桃花峪以下为下游.数学的发展史一般分为四个时期（有很多分法），即数学的萌芽时期，古代数学时期，近代数学时期和现代数学时期。

一、数学萌芽时期（公元前6世纪以前）1.“数”概念的产生早在远古时代，人类就已具备了识别事物多少的能力。

数学的精确性
数学的精确性，确切地说是指逻辑的严格 性和结论的确定性．数学推理和论断证明 对于每个了解它的人来说，都是确定无疑 和无可争辩的．这点对于其他学科影响很 大，以致有些学科中的理论，如果不能上 升到用数学模型表达就不能令人信服．
数学的广泛应用性
数学的广泛应用性是任何其他学科所不能比拟的．几 乎所有学科都或多或少地应用着数学．天气预报、地 震预报离不开数学；电影电视中引人入胜的动画制作， 离不开数学；经济学离不开数学；力学、物理学以及 天文学上的定律就是用数学公式的形式来描述的。过 去化学和生物学与数学联系较少，现在也需要借助数 学来发展自己．农业方向要想提高农产品的产量和质 量，就需要应用试验设计和优选法；兴修水利，防止 堤坝渗水则需用到更高深的数学知识．没有数学的发 展，卫星就上不了天；没有数学的发展，人类就不可 能遨游太空．
亚历山大里亚的欧几里得，古希腊数学 家，被称为“几何之父”。他活跃于托 勒密一世（公元前323年－前283年）时
期的亚历山大里亚，他最著名的著作 《几何原本》是欧洲数学的基础，提出 五大公设，发展欧几里得几何，被广泛 的认为是历史上最成功的教科书。欧几 里得也写了一些关于透视、圆锥曲线、 球面几何学及数论的作品,是几何学的奠
学》。非欧几何是人类认识史上一个富 有创造性的伟大成果，它的创立，不仅 带来了近百年来数学的巨大进步，而且 对现代物理学、天文学以及人类时空观 念的变革都产生了深远的影响。
• 尼耳期·亨利克·阿贝尔（N.H.Abel， 1802－1829）1802年8月出生于挪威 西南城市斯塔万格附近的芬岛的一个 农村。他很早便显示了数学方面的才 华。他得出了椭圆函数的基本性质， 找到了与三角函数中的π有相似作用 的常数K，证明了椭圆函数的周期性。 他建立了椭圆函数的加法定理，借助 于这一定理，又将椭圆函数拓广到整 个复域，并因而发现这些函数是双周 期的，这是别开生面的新发现；他进 一步提出一种更普遍更困难类型的积 分——阿贝尔积分，并获得了这方面 的一个关键性定理，即著名的阿贝尔 基本定理，它是椭圆积分加法定理的 一个很宽的推广。至于阿贝尔积分的 反演——阿贝尔函数，则是不久后由 黎曼首先提出并加以深入研究的。