一元线性回归效果的显著性检验

线性回归的显着性检验1.回归方程的显着性在实际问题的研究中,我们事先并不能断定随机变量y 与变量p x x x ,,,21 之间确有线性关系,在进行回归参数的估计之前,我们用多元线性回归方程去拟合随机变量y 与变量p x x x ,,,21 之间的关系,只是根据一些定性分析所作的一种假设;因此,和一元线性回归方程的显着性检验类似,在求出线性回归方程后,还需对回归方程进行显着性检验;设随机变量Y 与多个普通变量p x x x ,,,21 的线性回归模型为其中ε服从正态分布),0(2σN对多元线性回归方程的显着性检验就是看自变量若接受p x x x ,,,21 从整体上对随机变量y 是否有明显的影响;为此提出原假设如果0H 被接受,则表明随机变量y 与p x x x ,,,21 的线性回归模型就没有意义;通过总离差平方和分解方法,可以构造对0H 进行检验的统计量;正态随机变量n y y y ,,,21 的偏差平方和可以分解为：∑=-=n i i T y y S 12)(为总的偏差平方和,∑=-=n i i R y y S 12)ˆ(为回归平方和,∑=-=n i i i E yy S 12)ˆ(为残差平方和;因此,平方和分解式可以简写为： 回归平方和与残差平方和分别反映了0≠b 所引起的差异和随机误差的影响;构造F 检验统计量则利用分解定理得到：在正态假设下,当原假设0,,0,0:210===p b b b H 成立时,F 服从自由度为)1,(--p n p 的F 分布;对于给定的显着水平α,当F 大于临界值)1,(--p n p 时,拒绝0H ,说明回归方程显着,y x 与有显着的线性关系;实际应用中,我们还可以用复相关系数来检验回归方程的显着性;复相关系数R 定义为：平方和分解式可以知道,复相关系数的取值范围为10≤≤R ;R 越接近1表明E S 越小,回归方程拟合越好;2.回归系数的显着性若方程通过显着性检验,仅说明p b b b b ,,,210不全为零,并不意味着每个自变量对y 的影响都显着,所以就需要我们对每个自变量进行显着性检验;若某个系数0=j b ,则j x 对y 影响不显着,因此我们总想从回归方程中剔除这些次要的,无关的变量;检验i x 是否显着,等于假设已知])(,[~ˆ12-'X X B N B σ,p j i c X X ij ,,2,1,0,)(1 =='-）（记,可知],[~ˆ2σijj j c b N b ,,,2,1,0p j =据此可构造t 统计量 其中回归标准差为当原假设0:0=j j b H 成立时,则j t 统计量服从自由度为1--p n 的t 分布,给定显着性水平α,当2αt t j ≥时拒绝原假设0:0=j j b H ,认为j x 对y 影响显着,当2αt t j <时,接受原假设0:0=j j b H ,认为j x 对y 影响不显着;。

回归方程的显著性检验回归方程的显著性检验的目的是对回归方程拟合优度的检验。

F检验法是英国统计学家Fisher提出的，主要通过比较两组数据的方差S2，以确定他们的精密度是否有显著性差异。

回归方程显著性检验具体方法为：由于y的偏差是由两个因素造成的，一是x变化所引起反应在S回中，二是各种偶然因素干扰所致S残中。

将回归方程离差平方和S回同剩余离差平方和S残加以比较，应用F检验来分析两者之间的差别是否显著。

如果是显著的，两个变量之间存在线性关系；如果不显著，两个变量不存在线性相关关系。

n个观测值之间存在着差异，我们用观测值yi与其平均值的偏差平方和来表示这种差异程度，称其为总离差平方和，记为由于所以式中称为回归平方和，记为S回。

称为残差平方和，记为。

不难证明，最后一项。

因此S总＝S回＋S残上式表明，y的偏差是由两个因素造成的，一是x变化所引起，二是各种偶然因素干扰所致。

事实上，S回和S残可用下面更简单的关系式来计算。

具体检验可在方差分析表上进行。

这里要注意S回的自由度为1，S残的自由度为n－2，S总的自由度为n－1。

如果x与y有线性关系，则其中，F（1，n-2）表示第一自由度为1，第二自由度为n-2的分布。

在F表中显著性水平用表示，一般取0.10，0.05，0.01，1-表示检验的可靠程度。

在进行检验时，F值应大于F表中的临界值Fα。

若F<0.05(1,n-2)，则称x与y 没有明显的线性关系，若F0.05(1,n-2)<F<F0.01(1,n-2)，则称x与y有显著的线性关系；若F>F0.01(1,n-2)，则称x与y有十分显著的线性关系。

当x与y有显著的线性关系时，在表2-1-2的显著性栏中标以〝*〞；当x与y有十分显著的线性关系时，标以〝**〞。

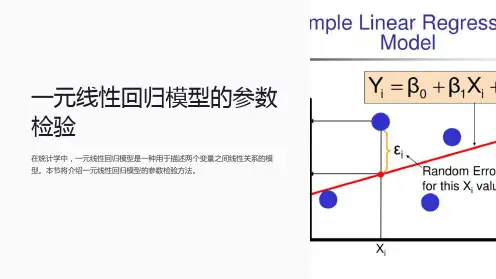
一元线性回归效果的显著性检验(F检验法)前面我们给出了一元回归直线方程的求解即一元线性回归中未知参数的最小二乘估计．那么这条回归直线对观测数据(x i,y i) (i=1,2,…,n) 拟合的程度如何？是否真正体现x、y 之间的这种线性关系，这就需要对回归效果的好坏进行检验．这种检验是评价方程对总体的代表性的所谓线性关系的显著性检验．检验x与y是否具有线性关系，以及它们之间的密切程度，这就是回归直线方程的效果检验所要解决的问题．由一元线性回归的数学模型可知，一元线性回归的数学模型是y=a+bx+εε～N(0, σ2)即随机变量y的数学期望是自变量x的线性函数，然而这样的假设是否合理呢？若在y=a+bx+ε中b=0，说明x的变化对y没有影响，这时回归方程就不能近似地描述变量x与y之间的关系，因此为了判断x与y之间是否存在线性关系，只需检验假设：H0：b=0此问题也称为线性回归方程的显著性检验问题．我们要根据观测数据(x i,y i) (i=1,2,…,n)作出拒绝或接受原假设b=0的判断．拒绝原假设才能确认我们的线性回归模型是合理的，接受原假设表示不能认为x、y之间有线性相关关系．如何构造统计量来检验这个假设问题呢？我们先把变量y的离差平方和予以分解.（点击此处看分解过程）=Q+U其中是回归值与其平均值的离差平方和，而,可以把看成是由于x的变化而引起的y值变化，因此称之为回归平方和；反映的是观测值与回归值之间的离差平方和，它表示除x对y的线性影响之外的一切因素引起的y值的变化，称之为误差平方和或残差平方和.而∴数学上我们可以证明,当H0为真时,统计量～F(1, n-2).对于给定的显著性水平α,查自由度为(1，n-2)的F分布临界值表,可得临界值Fα(1, n-2) 使得.其拒绝域为W={F>Fα(1, n-2)}.例在某大学一年级新生体检表中,随机抽取10张,得到10名大学生的身高(x)和体重(y)的数据如下,试求体重关于身高的线性回归方程,并检验回归方程的显著性(α=0.05)?身高x i/cm 体重y i/kg 身高x i/cm 体重y i/kg162 170 166 158 174 51545247631661671701731685955605754解.根据表中数据,列出下列计算表. 回归直线方程的计算步骤(I)i x i y i x i2y i 2x i y i1 2 3 4 5 6 7 8 9 10 Σ1621701661581741661671701731681674515452476359556057545522624428900275562496430276275562788928900299292822428043826012916270422093969348130253600324929163067082629180863274261096297949185102009861907292574,,,,,∴,.因此线性回归方程为:.下面我们来检验身高x与体重y之间是否具有显著的线性关系．根据题意,我们作假设H0: b=0 . n=10 ,,,∴.对于给定的α=0.05,查F分布临界值表得到临界值:F0.05(1, 8)=5.32．显然，F0=19.12> F0.05(1, 8)=5.32，故拒绝H0，即由F检验法可知，身高x与体重y 之间的线性关系是显著的，且它们之间的关系为：.。

§2.4 一元线性回归的模型检验一、经济意义检验。

二、在一元回归模型的统计检验主要包括如下几种检验1、拟合优度检验(R2检验;2、自变量显著性检验(t检验;3、残差标准差检验(SE检验。

•主要检验模型参数的符号、大小和变量之间的相关关系是否与经济理论和实际经验相符合。

一、经济意义检验i•二、统计检验•回归分析是要通过样本所估计的参数来代替总体的真实参数,或者说是用样本回归线代替总体回归线。

•尽管从统计性质上已知,如果有足够多的重复抽样,参数的估计值的期望(均值就等于其总体的参数真值,但在一次抽样中,估计值不一定就等于该真值。

那么,在一次抽样中,参数的估计值与真值的差异有多大,是否显著,这就需要进一步进行统计检验。

1、拟合优度检验拟合优度检验:对样本回归直线与样本观测值之间拟合程度的检验。

度量拟合优度的指标:判定系数(可决系数R2(1、总离差平方和的分解已知由一组样本观测值(X i ,Y i ,通过估计得到如下样本回归直线ii X Y 10ˆˆˆββ+=i i i i i i i y e Y Y Y Y Y Y y ˆˆ(ˆ(+=-+-=-=总离差平方和的分解ii X Y 10ˆˆˆββ+=ˆ(ˆY Y y i i -=i i i i i i i ye Y Y Y Y Y Y y ˆˆ(ˆ(+=-+-=-=Y 的i 个观测值与样本均值的离差由回归直线解释的部分回归直线不能解释的部分离差分解为两部分之和总离差平方和的分解公式:TSS=RSS+ESS,TSS 总离差平方和,ESS 为回归平方和,RSS 为残差平方和.((((((((0ˆˆˆ,0.0ˆˆ(ˆ(ˆˆ(2ˆˆ: 1022222222ˆˆˆˆˆˆ=+===-=-=--+=+=-+-=-+--+-=-+-=-=∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑ii i i i i ii i i i i i i i i i i i i i i i i i i i i i X e e Y e e e Y Y e Y Y e Y Y ESS RSS y e Y Y Y Y TSS Y Y Y YY Y Y YY Y Y Y Y Y Y Y ββ而因为证明TSS=ESS+RSSY的观测值围绕其均值的总离差(total variation可分解为两部分:一部分来自回归线(ESS,另一部分则来自随机部分(RSS。

从统计学看线性回归（2）——⼀元线性回归⽅程的显著性检验⽬录1. σ2 的估计2. 回归⽅程的显著性检验 t 检验（回归系数的检验） F 检验（回归⽅程的检验） 相关系数的显著性检验 样本决定系数 三种检验的关系⼀、σ2 的估计 因为假设检验以及构造与回归模型有关的区间估计都需要σ2的估计量，所以先对σ2作估计。

通过残差平⽅和（误差平⽅和）（1）（⽤到和，其中）⼜∵（2）∴（3）其中为响应变量观测值的校正平⽅和。

残差平⽅和有n-2 个⾃由度，因为两个⾃由度与得到的估计值与相关。

（4）（公式（4）在《线性回归分析导论》附录C.3有证明）∴σ2的⽆偏估计量：（5）为残差均⽅，的平⽅根称为回归标准误差，与响应变量y 具有相同的单位。

因为σ2取决于残差平⽅和，所以任何对模型误差假设的违背或对模型形式的误设都可能严重破坏σ2的估计值的实⽤性。

因为由回归模型残差算得，称σ2的估计值是模型依赖的。

⼆、回归⽅程的显著性检验 ⽬的：检验是否真正描述了变量 y 与 x 之间的统计规律性。

假设：正态性假设（⽅便检验计算）1. t 检验 ⽤t 检验来检验回归系数的显著性。

采⽤的假设如下：原假设 H0：β1 = 0 （x 与 y 不存在线性关系）对⽴假设 H1：β1 ≠ 0 回归系数的显著性检验就是要检验⾃变量 x 对因变量 y 的影响程度是否显著。

下⾯我们分析接受和拒绝原假设的意义。

（1）接受 H0：β1 = 0 （x 与 y 不存在线性关系） 此时有两种情况，⼀种是⽆论 x 取值如何， y 都在⼀条⽔平线上下波动，即，如下图1，另⼀种情况为， x 与 y 之间存在关系，但不是线性关系，如图2。

图 1图 2 （2）拒绝 H0：β1 = 0 （x 对解释 y 的⽅差是有⽤的） 拒绝原假设也有两种情况，⼀种是直线模型就是合适的，如图 3，另⼀种情况为存在 x 对 y 的线性影响，也可通过 x 的⾼阶多项式得到更好的结果，如图 4。