极化恒等式

极化恒等式定义极化恒等式定义是线性代数中的一个重要概念，它可以用于解决许多矩阵运算的问题。

在此，我们将分步骤阐述什么是极化恒等式定义，以及它的应用。

第一步：什么是极化恒等式定义极化恒等式定义指的是用内积表示一个对称双线性函数的方法，即将一个对称双线性函数转化为一个内积。

例如，假设$\langle\cdot,\cdot\rangle$是$V$上的一个内积，$f:V\timesV\rightarrow K$是$V$上的一个对称双线性函数，那么可以通过下列公式来定义$f$:$$f(x,y) = \frac{1}{2}\left(\langle x,y\rangle + \langle y,x\rangle\right)$$其中$K$表示一个数域，例如实数域或复数域。

第二步：极化恒等式定义的应用除了用于表示对称双线性函数之外，极化恒等式定义还可以用于求解矩阵的特征值和特征向量。

假设$A$是一个矩阵，那么$A$的特征向量为非零向量$x\in R^n$，满足$Ax=\lambda x$，其中$\lambda$是$A$的特征值。

那么可以通过极化恒等式定义来计算$A$的特征向量和特征值。

具体来说，我们可以先将$A$表示为一个对称双线性函数$f(x,y)=x^TAy$，然后根据极化恒等式定义，可以得到$$f(x,x) = \frac{1}{2}\left(\langle x,Ax\rangle +\langle Ax,x\rangle\right) = \frac{1}{2}(x^TAx + x^T(Ax)^T) = x^T\left(\frac{A + A^T}{2}\right)x$$其中$A^T$表示$A$的转置矩阵。

因为$A$是对称矩阵，所以$A=A^T$，因此可以得到$f(x,x)=x^TAx$。

此时，$A$的特征值和特征向量就可以通过求解$f(x,x)=\lambda x^Tx$的解来得到。

总之，极化恒等式定义是线性代数中的一个重要概念，它可以被用于许多矩阵运算的问题。

极化恒等式三角公式极化恒等式是数学中的基本公式之一。

在三角函数中，这个公式被广泛地应用于推导其他的三角函数公式。

以下是关于极化恒等式以及三角公式方面的详细介绍。

一、极化恒等式极化恒等式的公式如下：$2\cos A\cos B=\cos (A+B) + \cos (A-B)$$2\sin A\sin B=\cos (A-B) - \cos (A+B)$$2\sin A\cos B=\sin (A+B) + \sin (A-B)$这一公式的含义是，可以把两个三角函数写成另外两个三角函数的和或差的形式。

其中，第一个公式是余弦定理的另一种形式，第二个公式可以用来导出一些三角函数的重要性质，第三个公式则可以用于求解三角方程。

二、三角公式1. 倍角公式倍角公式可以用来求解一些复杂的三角函数问题：$ \sin 2A= 2\sin A\cos A $$ \cos 2A= \cos^2 A - \sin^2 A $$ \cos 2A= 2\cos^2 A - 1 $2. 和差公式和差公式可以用来把两个三角函数的和或差写成一种更简单的形式：$ \sin(A+B) = \sin A\cos B + \cos A\sin B $$ \sin(A-B)= \sin A\cos B - \cos A\sin B $$ \cos(A+B)= \cos A\cos B - \sin A\sin B $$ \cos(A-B)= \cos A\cos B + \sin A\sin B $3. 半角公式半角公式可以用来把一个角的三角函数值拆分成一个底角的三角函数值：$ \sin\frac{A}{2}= \pm \sqrt{\frac{1-\cos A}{2}} $$ \cos\frac{A}{2}= \pm \sqrt{\frac{1+\cos A}{2}} $$ \tan\frac{A}{2}= \pm \sqrt{\frac{1-\cos A}{1+\cos A}} $这些公式可以用于求解一些关于角度的三角函数的问题，比如说，可以用半角公式把 $\sin\frac{\pi}{8}$ 转化成更简单的形式。

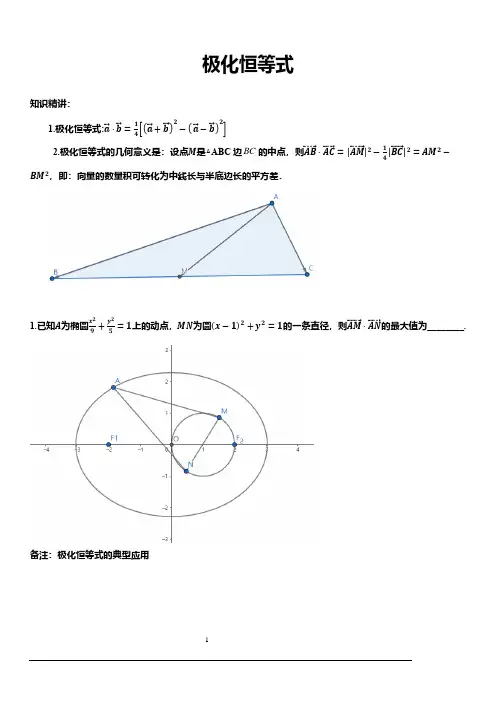
极化恒等式知识精讲：1.极化恒等式:a ⃗ ⋅b ⃗ =14[(a ⃗ +b ⃗ )2−(a ⃗ −b⃗ )2] 2.极化恒等式的几何意义是：设点M 是△ABC 边的中点，则AB⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AM ⃗⃗⃗⃗⃗⃗⃗ |2−14|BC ⃗⃗⃗⃗⃗⃗ |2=AM 2−BM 2，即：向量的数量积可转化为中线长与半底边长的平方差．1.已知A 为椭圆x 29+y 25=1上的动点，MN 为圆(x −1)2+y 2=1的一条直径，则AM ⃗⃗⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ 的最大值为________.备注：极化恒等式的典型应用BC2. （三星）（2017全国2理）已知ΔABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA ⃗⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )的最小值是（ ）A.−2B.−32 C. −43 D.−1 解：方法一：建系法连接OP ，OA⃗⃗⃗⃗⃗⃗ =(0,√3)，OB ⃗⃗⃗⃗⃗⃗ =(−1,0)，OC ⃗⃗⃗⃗⃗⃗ =(1,0). PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(−x,−y )⋅(−x,√3−y) ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =x 2+y 2−√3y =x 2+(y −√32)2−34 ∴PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−34，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32 ∴最小值为−32方法二：均值法∵PC ⃗⃗⃗⃗⃗ +PB⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ，∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ 由上图可知：OA ⃗⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗⃗ −PO ⃗⃗⃗⃗⃗⃗ ；两边平方可得3=(PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ∵ (PA ⃗⃗⃗⃗⃗⃗ )2+(PO ⃗⃗⃗⃗⃗⃗ )2≥−2PA ⃗⃗⃗⃗⃗⃗ ⋅PO ⃗⃗⃗⃗⃗⃗ ，∴ 2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32∴ PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ ≥−32，∴最小值为−32 解法三：配凑法 ∵PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ =2PO ⃗⃗⃗⃗⃗⃗ ∴PA ⃗⃗⃗⃗⃗⃗ ⋅(PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗⃗ )=2PO ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗⃗ =(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(PO ⃗⃗⃗⃗⃗⃗ −PA ⃗⃗⃗⃗⃗⃗ )22=(PO⃗⃗⃗⃗⃗⃗ +PA ⃗⃗⃗⃗⃗⃗ )2−(AO ⃗⃗⃗⃗⃗⃗ )22≥−32∴最小值为−323．在∆ABC 中，BC 边上的中线AD 的长为2，点P 是∆ABC 所在平面上的任意一点，则PA PB PA PC ⋅+⋅的最小值为 A ．1B ．2C ．-2D ．-1【详解】建立如图所示的平面直角坐标系，使得点D 在原点处，点A 在y 轴上，则A (0,2)．设点P 的坐标为x y (,)，则(,2),(,)PA x y PO x y =−−=−−， 故()22(2)PA PB PA PC PA PB PC PA PO x y y ⋅+⋅=⋅+=⋅=+−22=+−−≥−x y 2[(1)]2222，当且仅当==x y 0,1时等号成立．所以PA PB PA PC ⋅+⋅的最小值为−2．选C ．4. （武汉二中高二）已知圆M:x 2+(y −1)2=1, 圆N:x 2+(y +1)2=1, 直线l 1、l 2分别过圆心M ,且l 1与圆M 相交于A 、B , l 2与圆N 相交于C 、D , P 是椭圆x 23+y 24=1上的任意一动点, 则PA → ⋅PB → +PC → ⋅PD →的最小值为______________.6 备注：用到极化恒等式5．在平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，若BE →=EF →=FG →=GC →，则2AE →∙DC →+AE →∙AF →=_____；若P 为边BC 上一动点，当PA →∙PC →取最小值时，则cos ∠PDC 的值为_____．解：∵平面四边形ABCD 中，===AB BC CD 22，∠ABC =60∘,∠ADC =90∘，∴△ABC 是边长为2的等边三角， 在Rt △ADC 中，AC =2,CD =1，所以∠ACD =60∘，又BE →=EF →=FG →=GC →， ∴E,F,G 是BC 边的四等分点．如图建立坐标系：则：A(0,√3),B (−1,0),C (1,0)， D (32,√32),E (−12,0),F (0,0),G (12,0)， 所以2AE →DC →+AE →AF →=2(−12,−√3)(−12,−√32)+(−12,−√3)(0,−√3)=132，再设P (x,0)，则−1≤x ≤1，∴PA →PC →=(−x,√3)(1−x,0)=x 2−x =(x −12)2−14，显然x =12时，PA →PC →最小，此时P (12，0)，∴cos ∠PDC =cos ⟨DP →，DC →⟩=(−1，−√3)⋅(−1，−√3)(−1)+(−√32)(−12)+(−√32)=5√714．故答案为：132，5√714．6．在△OAB 中，OA =OB =2，AB =2√3，动点P 位于直线OA 上，当PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值时，向量PA ⃗⃗⃗⃗⃗⃗ 与PB ⃗⃗⃗⃗⃗⃗ 的夹角余弦值为（ ）A ．−3√77B ．7C ．−√217D ．√213【详解】∵|AB ⃗⃗⃗⃗⃗⃗ |2=(OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗⃗ )2=OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ ，即8−2OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =12，∴OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =−2， 设OP ⃗⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗⃗ (0≤λ≤1)，PA ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ，PB ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −OP ⃗⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ ， 所以，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ =(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅(OB ⃗⃗⃗⃗⃗⃗ −λOA ⃗⃗⃗⃗⃗⃗ )=(1−λ)OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ +λ(λ−1)OA⃗⃗⃗⃗⃗⃗ 2 =−2(1−λ)+4λ(λ−1)=4λ2−2λ−2=(2λ−12)2−94，当λ=14时，PA ⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ 取得最小值−94，此时|PA ⃗⃗⃗⃗⃗⃗ |=34|OA ⃗⃗⃗⃗⃗⃗ |=32， |PB ⃗⃗⃗⃗⃗⃗ |2=|OB ⃗⃗⃗⃗⃗⃗ −14OA⃗⃗⃗⃗⃗⃗ |2=116OA ⃗⃗⃗⃗⃗⃗ 2+OB ⃗⃗⃗⃗⃗⃗ 2−12OA ⃗⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =116×22+22−12×(−2)=214，所以，|PB ⃗⃗⃗⃗⃗⃗ |=√212，则cos <PA⃗⃗⃗⃗⃗⃗ ,PB ⃗⃗⃗⃗⃗⃗ >=PA⃗⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗⃗ |PA⃗⃗⃗⃗⃗⃗ |⋅|PB ⃗⃗⃗⃗⃗⃗ |=−9432×√212=−√217. 故选：C.7. （三星）在锐角∆ABC 中已知B= 3，|AB ⃗⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ |=2,则AB ⃗⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ 的取值范围是__________.解：法一：极化恒等式；法二：以B 为原点，BA 所在直线为x 轴建立坐标系，因为设A（x ，0）因为△ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°，即A 在如图的线段DE 上（不与D ，E 重合），所以1＜x ＜4，则AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ =x 2﹣x=（x ﹣12）2﹣14，所以AB ⃗⃗⃗⃗⃗⃗ AC ⃗⃗⃗⃗⃗ 的范围为（0，12）．方法2∵∠B=π3， △ABC 是锐角三角形，所以A+C=120°，∴30°＜A ＜90°=a=2由正弦定理可得()−==A B a b csin 120sinA sin 0∴=b ,=−Ac A sin 2sin 1200)( ∴120cos cos AB AC c b A A ===+=+⎝⎭−AA Asin tan 32202)(∵∈tanA0,3)( ∴(0,12AB AC ∈)8.在△ABC 中，AC ＝2BC ＝4，∠ACB 为钝角，M ，N 是边AB 上的两个动点，且MN ＝1，若CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ 的最小值为34，则cos ∠ACB ＝ ． 【答案】1−3√58【解析】取MN 的中点P ，则由极化恒等式得CM ⃗⃗⃗⃗⃗⃗ ⋅CN⃗⃗⃗⃗⃗⃗ =|CP ⃗⃗⃗⃗⃗ |2−14|MN ⃗⃗⃗⃗⃗⃗⃗ |2=|CP ⃗⃗⃗⃗⃗ |2−14∵CM ⃗⃗⃗⃗⃗⃗ ⋅CN ⃗⃗⃗⃗⃗⃗ 的最小值为34∴|CP ⃗⃗⃗⃗⃗ |min 由平几知识知：当CP ⊥AB 时，CP 最小. 如图，作CH ⊥AB ，H 为垂足，则CH=1 又AC ＝2BC ＝4，所以∠B ＝30o ，sinA=14 所以cos ∠ACB ＝cos （150o －A ）=1−3√58.9.如图所示，矩形ABCD 的边AB=4，AD=2，以点C 为圆心，CB 为半径的圆与CD 交于点E ，若点P 是圆弧EB ̂ (含端点B 、E)上的一点，则PA → ·PB → 的取值范围是 .H【解析】取AB 的中点设为O ，则， 当O 、P 、C 共线时， PO 取得最小值为PO =2√2−2；当P 与B （或E ）重合时，PO 取得最大值为PO=2， 所以的取值范围是.10.如图，是边长为P 是以C 为圆心，1为半径的圆上的任意一点，则AP⃗⃗⃗⃗⃗⃗ ∙BP ⃗⃗⃗⃗⃗⃗ 最小值是_____.－111.（三星）如图，在△ABC 中，D 是BC 的中点，E,F 是AD 上的两个三等分点，BA ⃗⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ =4,BF ⃗⃗⃗⃗⃗⃗ ⋅CF ⃗⃗⃗⃗⃗ =−1,则BE ⃗⃗⃗⃗⃗⃗ ⋅CE ⃗⃗⃗⃗⃗ 的值是________.备注：极化恒等式的典型应用2221=4PA PB PO AB PO ⋅−=−4PA PB ⋅−[8∆ABC CA BP12.若平面向量a ，b 满足|2a －b|≤3，则a·b 的最小值为________.【解析】根据极化恒等式得：8a ⋅b =(2a +b)2−(2a −b)2=(2a +b)2−9≥−9，故a ⋅b ≥−98，所以a ⋅b 的最小值为−98．13.已知平面向量a ，b ，e 满足|e|＝1，a·e ＝1，b·e ＝－2，|a ＋b|＝2，那么a·b 的最大值为________． 解： 由a·e ＝1，b·e ＝－2得: a·e －b·e ＝3，即（a －b ）·e ＝3，|a －b|cos θ＝3a·b=14[|a ＋b|2－|a －b|2]≤－5414.在中，已知，，则面积的最大值是 ．解：取BC 的中点为D ，则AB ⃗⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =AD 2−BC24，所以AD =√2因为BC 边上的高线长不大于中线长，当中线就是高线时，面积最大，故．15.已知平面向量a ⃗ ,b ⃗ ,c ⃗ 满足|a ⃗ |=1，a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2，|2b ⃗ −c ⃗ |=2，那么b⃗ ⋅c ⃗ 的最小值为________． 【解析】由a ⃗ ⋅b ⃗ =12，a ⃗ ⋅c ⃗ =2得2a ⃗ ⋅b ⃗ +a ⃗ ⋅c ⃗ =3，即a ⃗ ⋅(2b ⃗ +c ⃗ )=3 又a ⃗ ⋅(2b ⃗ +c ⃗ )=|a ⃗ ||2b ⃗ +c ⃗ |cos θ（其中θ为向量a ⃗ 与2b ⃗ +c ⃗ 的夹角） 所以|2b⃗ +c ⃗ |=3cos θ所以b⃗ ⋅c ⃗ =18[(2b ⃗ +c ⃗ )2−(2b ⃗ −c ⃗ )2]=18(9cos 2θ−4)≥58.∆ABC =BC 21AB AC •=∆ABC ∆ABC16.已知锐角的外接圆的半径为1， ，则的取值范围为__________．17.已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则PA → ⋅PB →的取值范围是_____.[－2,6]18.在ΔABC 中，AB =3,AC =4,∠BAC =60°，若P 是ΔABC 所在平面内的一点，且AP =2，则PB → ⋅PC →的最大值为_____.10+2√3719.已知点P 是边长为2√3的正三角形ABC 内切圆上的一点，则PA → ⋅PB →的取值范围为_____.[−3,6]20.已知正方形ABCD 的边长为1，中心为O ，直线l 经过中心O ，交AB 于点M ，交CD 于点N ，P 为平面上一点，若2OP → ＝λOB → ＋(1－λ)OC → ，则PM → ·PN →的最小值为__________.−71621.设点P 为正三角形△ABC 的边BC 上的一个动点，当PA → ·PC →取得最小值时，sin ∠PAC 的值为________．√392622.在平面直角坐标系xOy 中，点A ，B 分别在x 轴，y 轴正半轴上移动，AB ＝2，若点P 满足PA → ·PB →＝2，则OP 的取值范围为________．[√3−1,√3+1]23.在△ABC 中，E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB → ·PC →＋BC →2的最小值是__________．4√3∆ABC ∠=πB 6BA BC⋅⎝ ⎛23,3。

极化恒等式补充1极化恒等式：()()2214a b a b a b ⎡⎤⋅=+--⎢⎥⎣⎦极化恒等式的几何意义是：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14，即222214a b AD BC AM BM ⎡⎤⋅=-=-⎣⎦ 2极化恒等式的应用例1ABC M BC AM=3BC=10AB AC=∆⋅ 在中，是的中点，，，则解析：221925162AB AC AM BC ⋅=-=-=- 00001ABC P AB P B=AB AB P 4PB PC P B P C ∆⋅≥⋅ 例2：设，是边上一定点，满足，且对于边上任意一点，恒有，则0.90A ABC ∠=0.90B BAC ∠=.C AB AC =.D AC BC=22022000000BC D PD P D PBC PB PC=PD BD P BC P B P C=P D ,PD P D P D AB AC=BCBD ∆⋅-∆⋅-≥⊥ 解析：取中点，连接，，在内使用极化恒等式得在内使用极化恒等式得由条件知，即，故3ABCD P AB APB PC PD f⋅ 例：设正方形的边长为4,动点在以为直径的圆弧上，则第三题图第四题图解析：[]24,225016.PC PD PE PE PC PD ⎡⎤⋅=-∈⋅∈⎣⎦由图知，，，故，2min ABC 4ABC E F AB AC P EF S =2PC PB+BC =∆⋅ 例：在中，点，分别是线段，的中点，点在直线上，若，则2222222421322,,,44434+BC 23PD BC BC=.43BCPBC PC PB PD BC PC PB BC PD BC h PD BC BC PC PB BC ⋅=-⋅+=+=≥⋅+≥≥⊥ 解析：因此，当且仅当，时等号成立051AOB AOB=60C AB OC P OP BP ∠⋅ 例：如图，在半径为的扇形中，，为弧上的动点，与交于点，则的最小值为解析：如上图所示，213311,PD ,442162OP BP PD OP BP ⎡⎤⎡⎤⋅=-∈⋅∈-⎢⎥⎢⎥⎣⎦⎣⎦ 易知，，则()6ABCD OB OC ⋅ 例：如图放置的边长为1的正方形顶点分别在x轴，y轴正半轴含原点滑动，则的最大值为22111OB OC=OE 12424⎛⎫⋅-≤+-= ⎪⎝⎭ 解析：。

极化恒等式公式1、基本极化恒等式基本极化恒等式又称为Stokes方程，它是理解介质中电磁波传播的基本方程。

它由波动磁场场强E和磁场场强H的外场响应组成，可以概括为：E =εHH=-D其中ε表示极化率，D表示电导率。

我们可以从它推导出其他极化恒等式，如：2、垂直极化恒等式垂直极化恒等式又称为Faraday方程，它是介质中电磁波传播的重要方程，可以根据基本极化恒等式推导而来，它包括垂直极化分量的电离度、垂直极化作用的等效度以及垂直极化圆盘的传播常数等因素，可以表示为：Dtanθ=ε+ηV其中，θ表示极化角，η表示磁导率，V表示电位场的垂直极化分量。

3、水平极化恒等式水平极化恒等式由基本极化恒等式推导而来，它表达了水平极化作用的电离度、极化作用的等效度、电位场的水平极化分量以及水平极化圆盘的传播常数等因素，可以表示为：cosθ=ε+ηV其中，θ表示极化角，η表示磁导率，V表示电位场的水平极化分量。

4、反射极化恒等式反射极化恒等式可以由基本极化恒等式推导而来，用来研究电磁波在介质之间沿极化方向传播时所见到的反射现象。

这个公式可以表达用于反射电离度、等效度、反射圆盘传播常数以及反射角等因素，可以表示为：Et/Es=(ncosθ-μsinθ) / (ncosθ+μsinθ)其中，θ表示反射极化角，n为介质的电离度，μ为介质的等效度，Es 为入射波的强度，Et为反射波的强度。

5、传播极化恒等式传播极化恒等式凝结了电磁波在介质中沿一定方向传播时的电离度、等效度，以及传播极化圆盘的传播常数等因素，它可以由基本极化恒等式推出，可以表示为：H/E=ncosθ/μsinθ其中，θ表示传播极化角，n为介质的电离度，μ为介质的等效度，E 为入射波的强度，H为传播波的强度。

极化恒等式证明
极化恒等式公式为：当H是实空间时，(x，y)=(1/4)(‖x+y‖^2-‖x-y‖^2)；当H是复空间时，(x，y)=(1/4)(‖x+y‖^2-‖x-y‖^2+i‖x+iy‖^2-i‖x-iy‖^2)。

极化恒等式(polarization identity)是联系内积与范数的一个重要的等式，是用范数表示内积的公式。

设H是内积空间，‖·‖是由内积(·，·)导出的范数。

对于实内积空间上的双线性埃尔米特泛函以及复内积空间上的双线性泛函φ(x，y)也分别有类似于上述的恒等式。

极化恒等式之恒等式简介：
恒等式（identities），数学概念，恒等式是无论其变量如何取值，等式永远成立的算式。

恒等式成立的范围是左右函数定义域的公共部分，两个独立的函数却各自有定义域，与x在非负实数集内是恒等的，而在实数集内是不恒等的。

恒等式有多个变量的，也有一个变量的，若恒等式两边就一个变量，恒等式就是两个解析式之间的一种关系。

它来源于e^ix=cosx+isinx(复数的三角表示),令x=π就得e^πi + 1 = 0。

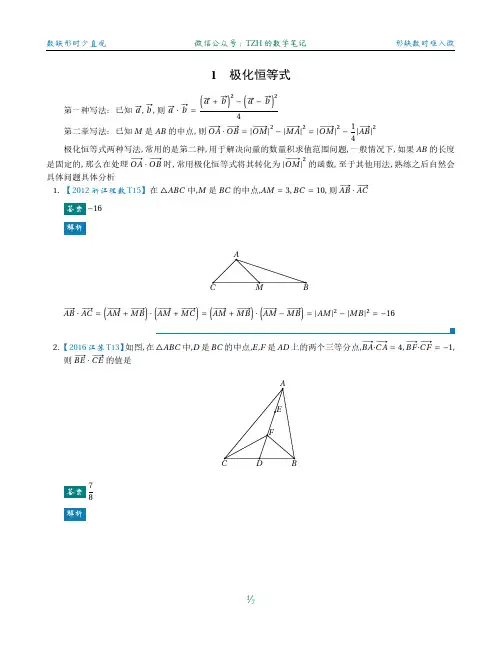
1极化恒等式第一种写法：已知#…a ,#…b ,则#…a ⋅#…b =⒧#…a +#…b ⒭2−⒧#…a −#…b ⒭24第二章写法：已知M 是AB 的中点,则# …OA ⋅# …OB =|# …OM|2−|# …MA|2=|# …OM|2−14|# …AB|2极化恒等式两种写法,常用的是第二种,用于解决向量的数量积求值范围问题,一般情况下,如果AB 的长度是固定的,那么在处理# …OA ⋅# …OB 时,常用极化恒等式将其转化为|# …OM|2的函数,至于其他用法,熟练之后自然会具体问题具体分析1.【2012浙江理数T15】在△ABC 中,M 是BC 的中点,AM =3,BC =10,则# …AB ⋅# …AC−16# …AB ⋅# …AC =⒧# …AM +# …MB⒭⋅⒧# …AM +# …MC ⒭=⒧# …AM +# …MB⒭⋅⒧# …AM −# …MB⒭=|AM|2−|MB|2=−162.【2016江苏T13】如图,在△ABC 中,D 是BC 的中点,E ,F 是AD 上的两个三等分点,# …BA⋅# …C A =4,# …BF⋅# …C F =−1,则# …BE ⋅# …C E的值是78记|BD|=x ,|DF|=y ,則4=# …BA ⋅# …C A =|AD|2−|BD|2=9y 2−x 2−1=# …BF ⋅# …C F =|DF|2−|BD|2=y 2−x 2⎧⎪⎪⎨⎪⎪⎩x 2=138y 2=58从而# …BE ⋅# …C E =|DE|2−|BD|2=4y 2−x 2=783.【2018天津理数T8】如图,在平面四边形ABC D 中,AB⊥BC ,AD⊥C D,∠BAD =120∘,AB =AD =1.若点E 为边C D 上的动点,则# …AE ⋅# …BE 的最小值为A.2116B.32C.2516D.3A取AB 中点F ,则# …AE ⋅# …BE =|# …EF|2−|# …AF|2当EF ⟂C D 时,|# …EF|取得最小值54,比时# …AE ⋅# …BE 取得最小值2116,选A4.【2013浙江理数T7】设△ABC ,P 0是边AB 上一定点,满足# …P 0B =14# …AB ,且对于边AB 上任一点P ,恒有# …PB ⋅# …PC ⩾# …P 0B ⋅# …P 0C ,则A.∠ABC =90∘ B.∠BAC =90∘C.AB =ACD.AC =BCD取AB,BC的中点D,E.则# …PB⋅# …PC=(# …PE+# …EB)⋅(# …PE−# …EB)=|PE|2−|EB|2⩾|P0E|2−|EB|2,所以|PE|⩾|P0E|,则必有P0E⟂AB,从而C D⟂AB,所以AC=BC,选择D5.【2017全国2卷理数T12】已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则# …PA⋅⒧# …PB+PC⒭的最小值是A.−2B.−32C.−43D.−1B取BC中点M,取AM中点N,则# …PA⋅(# …PB+# …PC)=2# …PA⋅# …PM=2⒧PN2−MN2⒭⩾−2MN2=−32,当PN重合时取到,所以所求最小值是−32,选择B6.【2020天津T15】如图,在四边形ABC D中,∠B=60∘,AB=3,BC=6,且# …AD=λ# …BC,# …AD⋅# …AB=−32,则(1)实数λ的最小值为(2)若M,N是线段BC上的动点,且|# …MN|=1,则# …DM⋅# …DN的最小值为A DB M N C(1)16(2)132# …AD⋅# …AB=λ# …BC⋅# …AB=−9λ=−32,所以λ=16.取MN中点E,则# …DM⋅# …DN=|DE|2−|MN|24当DE⟂BC时,取到最小值13 2.7.【2005江苏T18】在△ABC 中,O 为中线AM 上的一个动点,若AM =2,则# …OA ⋅⒧# …OB +# …OC ⒭的最小值为−2设|OM|=x ,则# …OA ⋅(# …OB +# …OC )=2# …OA ⋅# …OM =−2x(2−x)⩾−2,取等条件是x =1,故所求最小值为−28.【2012安徽理数T14】若|2#…a −#…b |⩽3,则#…a ⋅#…b 的最小值是−98#…a ⋅#…b =|2#…a +#…b |2−|2#…a −#…b |28⩾−|2#…a −#…b |28⩾−989.在平行四边形ABC D 中,AD =√2,AB =2.若# …BF =# …FC ,则# …AF ⋅# …DF72# …AF ⋅# …DF =(# …AB +# …BF)⋅(# …AB −# …BF)=|AB|2−|BF|2=7210.已知△ABC 中,AB =8,BC =10,AC =6,P 在平面ABC 内,且# …PB ⋅# …PC =−9,则|# …PA|的取值范围是[1,9]解析11.正方体ABC D −A 1B 1C 1D 1的棱长为2,MN 是它的内切球的一条弦（我们把球面上任意两点之间的线段称为球的弦）,P 为正方体表面上的动点,当弦MN 的长度最大是,# …PM ⋅# …PN 的取值范围是[0,2]解析12.在面积为2的平行四边形ABC D中,点P为直线AD上的动点,则# …PB⋅# …PC+# …BC2的最大值是2√3设M为BC的中点,由题意,# …PB⋅# …PC+BC2=PM2−14BC2+BC2=PM2+34BC2⩾√3⋅PM⋅BC⩾√3⋅2S△PBC=2√3.取等条件为PM=√32BC且PM⟂BC.故所求最小值为2√313.在半径为1的扇形AOB中,∠AOB=60∘,C为弧AB的动点,AB与OC交于点P,则# …OP⋅# …BP的最小值是−1 16解析14.已知正四面体ABC D的棱长为2,P是以棱BC为直径的球面上一动点,则# …PA⋅# …PD的最大值是A.1+√2B.3C.2+√2D.2(√2+1)D取AD中点E,BC中点F,则# …PA⋅# …PD=|PE|2−|AE|2=|# …PF+# …FE|2−1⩽(|# …PF|+|# …FE|)2−1=(1+√2)2−1=2+2√2,选D15.【成都七中23届高三上一诊模拟T16】已知A(2cos15∘,2sin15∘),O(0,0),且|# …OB|=|# …OC|=2,则# …AB⋅# …AC的取值范围[−2,16]如图方法1极化恒等式记M为BC的中点,由极化恒等式可知:# …AB⋅# …AC=# …AM2−# …BM2,易知OM⊥BC,所以# …BM2=# …OB2−# …OM2所以# …AB⋅# …AC=# …AM2−# …BM2=# …AM2+# …OM2−# …OB2=# …AM2+# …OM2−# …OA2由余弦定理可知# …AM 2+# …OM 2−# …OA 2=2|# …MA|⋅|# …MO|cos ∠AMO =2# …MA ⋅# …MO记D 为OA 的中点,再由极化恒等式可知2# …MA ⋅# …MO =2 # …MD 2−# …OD 2因为B ,C 是圆上任意两点(可重合)所以|# …MD|∈[0,3]所以−2⩽# …AB ⋅# …AC ⩽16方法2投影暂无16.【乐山市21届一诊T10】已知△ABC 是边长为2的等边三角形,点P 是△ABC 所在平面的内的一点,且BP =1,则当# …AP ⋅# …C P 取得最小值时,# …BP ⋅# …BC 的值是A.√3B.√32C.−√3D.−√32A 方法1建系建系如图A(0,√3),B(−1,0),C (1,0),设P(−1+cos θ,sin θ)# …AP ⋅# …C P =⒧−1+cos θ,sin θ−√3⒭(−2+cos θ,sin θ)=3−2√3sin ⒧θ+π3⒭当且仅当θ=π6+2kπ时取等,代入# …BP ⋅# …BC =√3方法2向量转换# …AP⋅# …C P=⒧# …AB+# …BP⒭⋅⒧# …C B+# …BP⒭=# …AB⋅# …C B+# …AB⋅# …BP+# …BP⋅# …C B+# …BP2=2√3+1+# …AB⋅# …BP+# …BP⋅# …C B下求# …AB⋅# …BP+# …BP⋅# …BP⋅# …C B的最小值# …AB⋅# …BP+# …BP⋅# …BP⋅# …C B=−2# …BM⋅# …BP=−2|# …BM|⋅|# …BP|cos∠PBM=−2√3cos∠PBM⩾−2√3,当∠PBM=0时取得最小值,代入# …BP⋅# …BC=√3方法3极化恒等式# …AP⋅# …C P=# …PM2−14# …AC2=# …PM2−1⩾3−2√3,当P在线段BM与圆B的交点P′时,取得最小值,代入# …BP⋅# …BC=√3。

数学极化恒等式数学极化恒等式是数学中的一个重要概念，它在求解复数运算、多项式拆分和向量运算中起到了至关重要的作用。

本文将从多个角度介绍数学极化恒等式，展示其在数学领域中的广泛应用。

首先，我们来了解一下什么是极化恒等式。

在数学中，极化恒等式是指通过极化恒等式可以将一个向量或数列拆成两个特定的数的和。

它的形式为：\[x = \frac{1}{2} \left( x + \overline{x} \right) +\frac{1}{2i} \left( x - \overline{x} \right)\]其中，\(x\)表示一个复数或向量，\(\overline{x}\)表示其共轭。

数学极化恒等式在求解复数运算中应用广泛。

复数可以表示为实部加上虚部的形式，而极化恒等式可以将复数拆分成实轴和虚轴上的两个数。

例如，对于一个复数\(z = a + bi\)，其中\(a\)为实部，\(b\)为虚部。

根据极化恒等式，可以得到：\[z = \frac{1}{2} \left( a + bi + a - bi \right) +\frac{1}{2i} \left( a + bi - a + bi \right)\]化简后得到：\[z = \frac{1}{2} \left( 2a \right) + \frac{1}{2i}\left( 2bi \right)\]继续化简可得：\[z = a + bi\]这就是复数的极化恒等式。

通过极化恒等式，我们可以将复数的实部和虚部分离出来，更方便进行计算和分析。

极化恒等式在多项式的拆分中也有重要应用。

对于一个多项式\(f(x)\)，它可以表示为一些特定数的和。

根据极化恒等式，可以将其拆分成实数和虚数的和。

例如，对于一个二次多项式\(f(x) = ax^2 + bx + c\)，其中\(a\)、\(b\)、\(c\)均为实数。

根据极化恒等式，可以得到：\[f(x) = \frac{1}{2} \left( ax^2 + bx + c + ax^2 - bx - c \right) + \frac{1}{2i} \left( ax^2 + bx + c - ax^2 + bx + c \right)\]化简后得到：\[f(x) = \frac{1}{2} \left( 2ax^2 \right) + \frac{1}{2i} \left( 2bx \right) + c\]继续化简可得：\[f(x) = ax^2 + bx + c\]这就是多项式的极化恒等式。