计量经济学第三章13题

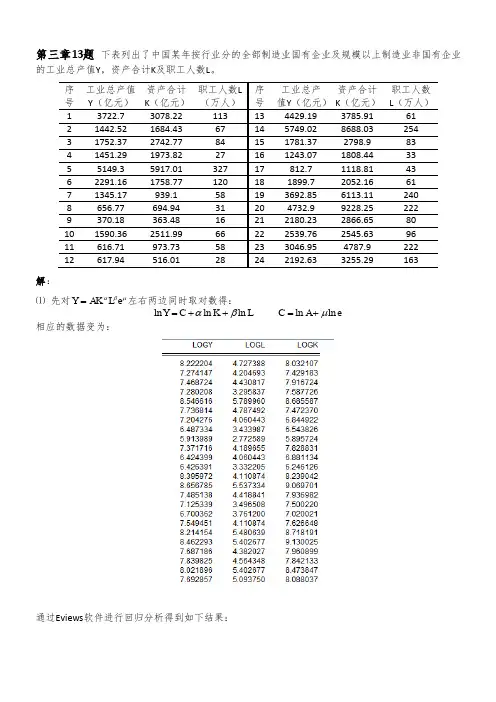
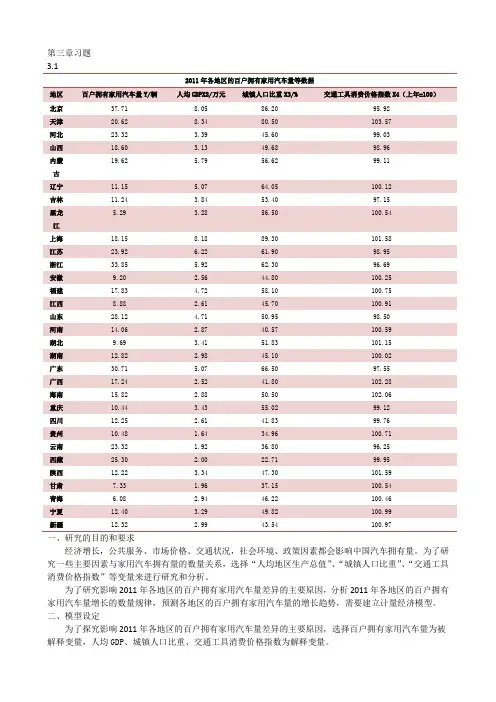
第三章习题3.12011年各地区的百户拥有家用汽车量等数据北京37.71 8.05 86.20 95.92天津20.62 8.34 80.50 103.57河北23.32 3.39 45.60 99.03山西18.60 3.13 49.68 98.9619.62 5.79 56.62 99.11内蒙古辽宁11.15 5.07 64.05 100.12吉林11.24 3.84 53.40 97.15黑龙5.29 3.28 56.50 100.54江上海18.15 8.18 89.30 101.58江苏23.92 6.22 61.90 98.95浙江33.85 5.92 62.30 96.69安徽9.20 2.56 44.80 100.25福建17.83 4.72 58.10 100.75江西8.88 2.61 45.70 100.91山东28.12 4.71 50.95 98.50河南14.06 2.87 40.57 100.59湖北9.69 3.41 51.83 101.15湖南12.82 2.98 45.10 100.02广东30.71 5.07 66.50 97.55广西17.24 2.52 41.80 102.28海南15.82 2.88 50.50 102.06重庆10.44 3.43 55.02 99.12四川12.25 2.61 41.83 99.76贵州10.48 1.64 34.96 100.71云南23.32 1.92 36.80 96.25西藏25.30 2.00 22.71 99.95陕西12.22 3.34 47.30 101.59甘肃7.33 1.96 37.15 100.54青海 6.08 2.94 46.22 100.46宁夏12.40 3.29 49.82 100.99新疆12.32 2.99 43.54 100.97一、研究的目的和要求经济增长，公共服务、市场价格、交通状况，社会环境、政策因素都会影响中国汽车拥有量。

一、单项选择题1．多元线性回归分析中（回归模型中的参数个数为k），调整后的可决系数与可决系数之间的关系（）A. B. ≥C. D.2．已知五元线性回归模型估计的残差平方和为，样本容量为46，则随机误差项的方差估计量为( )A. 33.33B. 40C. 38.09D. 203．多元线性回归分析中的 RSS反映了（）A．因变量观测值总变差的大小B．因变量回归估计值总变差的大小C．因变量观测值与估计值之间的总变差D．Y关于X的边际变化4．在古典假设成立的条件下用OLS方法估计线性回归模型参数，则参数估计量具有（）的统计性质。

A．有偏特性 B. 非线性特性C．最小方差特性 D. 非一致性特性5．关于可决系数，以下说法中错误的是（）A.可决系数的定义为被回归方程已经解释的变差与总变差之比B.C.可决系数反映了样本回归线对样本观测值拟合优劣程度的一种描述D.可决系数的大小不受到回归模型中所包含的解释变量个数的影响二、多项选择题1．调整后的判定系数与判定系数之间的关系叙述正确的有（）A.与均非负B.有可能大于C.判断多元回归模型拟合优度时，使用D.模型中包含的解释变量个数越多，与就相差越大E.只要模型中包括截距项在内的参数的个数大于1，则2．对多元线性回归方程（有k个参数）的显著性检验，所用的F统计量可表示为（）A. B.C. D.E.三、判断题1．在对参数进行最小二乘估计之前，没有必要对模型提出古典假定。

2．一元线性回归模型与多元线性回归模型的基本假定是相同的。

3．拟合优度检验和F检验是没有区别的。

参考答案：一、单项选择题1.A2.D3.C4.C5.D二、多项选择题1．CDE 2．BE三、判断题1．答：错误。

在古典假定条件下，OLS估计得到的参数估计量是该参数的最佳线性无偏估计（具有线性、无偏性、有效性）。

总之，提出古典假定是为了使所作出的估计量具有较好的统计性质以便进行统计推断。

2．答：错误。

在多元线性回归模型里除了对随机误差项提出假定外，还对解释变量之间提出无多重共线性的假定。

统计学2班第二次作业1、Ŷi =-151.0263 + 0.1179X 1i + 1.5452X 2iT= (-3.066806) (6.652983) (3.378064)R 2=0.934331 R 2=0.92964 F=191.1894 n=31⑴模型估计结果说明，各省市旅游外汇收入Y 受旅行社职工人数X 1，国际旅游人数X 2的影响。

由所估计出的参数可知，在假定其他变量不变的情况下，当旅行社职工人数每增加1人，各省市旅游外汇收入增加0.1179百万美元。

在嘉定其他变量不变的情况下。

当国际旅游人数每增加1万人，各省市旅游外汇收入增加1.5452百万美元。

⑵由题已知，估计的回归系数β1的T 值为：t （β1）=6.652983。

β2的T 值分为： t （β2）=3.378064。

α=0.05.查得自由度为n-2=22-2=29的临界值t 0.025(29)=2.045229因为t （β1）=6.652983≥t 0.025(29)=2.045229.所以拒绝原假设H 0：β1=0。

表明在显著性水平α=0.05下，当其他解释变量不变的情况下，旅行社职工人数X 1对各省市旅游外汇收入Y 有显著性影响。

因为 t （β2）=3.378064≥t 0.025(29)=2.045229，所以拒绝原假设H 0：β2=0表明在显著性水平α=0.05下，当其他解释变量不变的情况下，和国际旅游人数X 2对各省市旅游外汇收入Y 有显著性影响。

⑶正对H O ：β1=β2=0，给定显著水性水平α=0.05，自由度为k-1=2,n-k=28的临界值F 0.05（2,28）=3.34038。

由题已知F=191.1894>F 0.05（2,28）=3.34038，应拒绝原假设H O ：β1=β2=0，说明回归方程显著，即旅行社职工人数和旅游人数变量联合起来对各省市旅游外汇收入有显著影响。

2、⑴样本容量n=15 残差平方和RSS=66042-65965=77 回归平方和ESS 的自由度为K-1=2 残差平方和RSS 的自由度为n-k=13⑵可决系数R 2=TSS ESS =6604265965=0.99883 调整的可决系数R 2=1-（1-R 2）kn n --1=1-（1-0.99883）1214=0.99863 ⑶利用可决系数R 2=0.99883，调整的可决系数R 2=0.99863，说明模型对样本的拟合很好。

第三章练习题及参考解答3.1进入21世纪后，中国的家用汽车增长很快。

家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素，都会影响中国汽车拥有量。

为了研究一些主要因素与家用汽车拥有量的数量关系，选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量，2016年全国各省市区的有关数据如表3.5。

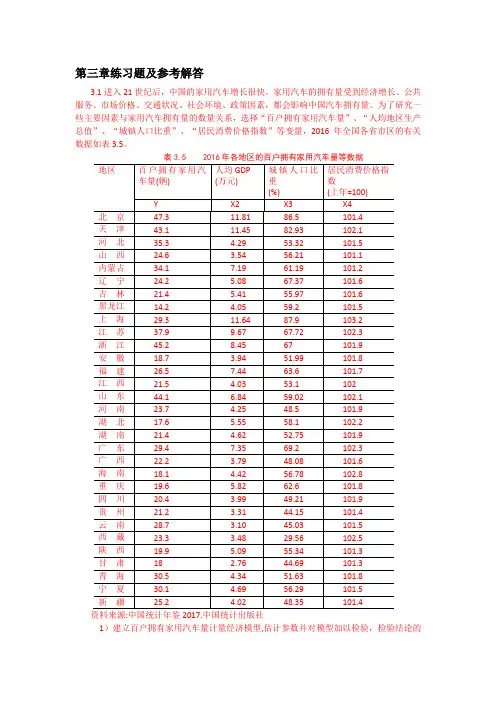
表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1）建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验，检验结论的依据是什么?。

2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】：1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007，可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。

解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=，表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。

2）X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。

由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。

汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。

第三章练习题及参考解答3.1为研究中国各地区入境旅游状况，建立了各省市旅游外汇收入（Y ，百万美元）、旅行社职工人数（X1，人）、国际旅游人数（X2，万人次）的模型，用某年31个省市的截面数据估计结果如下：ii i X X Y 215452.11179.00263.151ˆ++-= t=(-3.066806) (6.652983) (3.378064)R 2=0.934331 92964.02=R F=191.1894 n=31 1)从经济意义上考察估计模型的合理性。

2)在5%显著性水平上，分别检验参数21,ββ的显著性。

3)在5%显著性水平上，检验模型的整体显著性。

练习题3.1参考解答:(1)由模型估计结果可看出：从经济意义上说明，旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。

平均说来，旅行社职工人数增加1人，旅游外汇收入将增加0.1179百万美元；国际旅游人数增加1万人次，旅游外汇收入增加1.5452百万美元。

这与经济理论及经验符合，是合理的。

（2）取05.0=α，查表得048.2)331(025.0=-t因为3个参数t 统计量的绝对值均大于048.2)331(025.0=-t ，说明经t 检验3个参数均显著不为0，即旅行社职工人数和国际旅游人数分别对旅游外汇收入都有显著影响。

（3）取05.0=α，查表得34.3)28,2(05.0=F ，由于34.3)28,2(1894.19905.0=>=F F ，说明旅行社职工人数和国际旅游人数联合起来对旅游外汇收入有显著影响，线性回归方程显著成立。

3.2 表3.6给出了有两个解释变量2X 和.3X 的回归模型方差分析的部分结果：表3.6 方差分析表1）回归模型估计结果的样本容量n 、残差平方和RSS 、回归平方和ESS 与残差平方和RSS 的自由度各为多少?2）此模型的可决系数和调整的可决系数为多少?3）利用此结果能对模型的检验得出什么结论?能否确定两个解释变量2X 和.3X 各自对Y 都有显著影响? 练习题3.2参考解答:(1) 因为总变差的自由度为14=n-1，所以样本容量：n=14+1=15 因为 TSS=RSS+ESS 残差平方和RSS=TSS-ESS=66042-65965=77 回归平方和的自由度为：k-1=3-1=2 残差平方和RSS 的自由度为：n-k=15-3=12（2（3）这说明两个解释变量2X 和.3X 联合起来对被解释变量有很显著的影响，但是还不能确定两个解释变量2X 和.3X 各自对Y 都有显著影响。

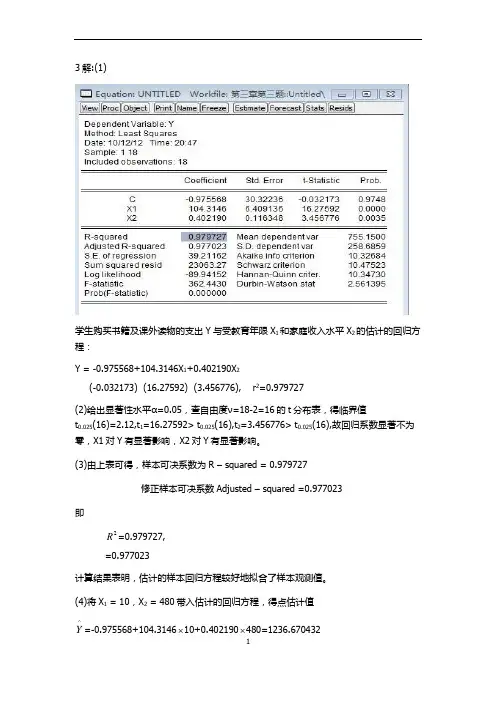
3解:(1)学生购买书籍及课外读物的支出Y与受教育年限X1和家庭收入水平X2的估计的回归方程：Y = -0.975568+104.3146X1+0.402190X2(-0.032173) (16.27592) (3.456776), r2=0.979727(2)给出显著性水平α=0.05，查自由度ν=18-2=16的t分布表，得临界值t0.025(16)=2.12,t1=16.27592> t0.025(16),t2=3.456776> t0.025(16),故回归系数显著不为零，X1对Y有显著影响，X2对Y有显著影响。

(3)由上表可得，样本可决系数为R – squared = 0.979727修正样本可决系数Adjusted – squared =0.977023即2R=0.979727,=0.977023计算结果表明，估计的样本回归方程较好地拟合了样本观测值。

(4)将X1 = 10，X2 = 480带入估计的回归方程，得点估计值^Y=-0.975568+104.3146⨯10+0.402190⨯480=1236.670432<1>根据（3.68）式求的^Y 方差的估计值 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∑∑∑∑∑∑∑∑66.21181122.379558.58282.379557241088.582810818'222122121121x x x x x x x x x x n X X 142359.4092661.021162.394801010000.00003.00008.00003.00267.00484.00008.00484.05980.0)480,10,1(21162.39)'()(22'191192^2=⨯=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤------⎢⎢⎢⎣⎡⨯==-X X X X Y S δ从而得到^227268.20142359.409)(==Y S对于给定的显著性水平05.0=α,查出自由度15=ν的t 分布双侧分位数13.2)15(2/05.0=t 得到置信度为95%的预测区间为)7545.1279,5863.1193(227268.2013.2670432.1236,227268.2013.2670432.1236()()(),()(^2/^^2/^=⨯+⨯-=⎪⎭⎫ ⎝⎛⋅+⋅-Y S t Y Y S t Y νναα<2>求的e 方差的估计值 6935.19462661.121162.394801010000.00003.00008.00003.00267.00484.00008.00484.05980.0)480,10,1(121162.39]')'(1[)(22191192^2=⨯=⎪⎭⎪⎬⎫⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------+⎪⎩⎪⎨⎧⨯=+=-X X X X e S δ从而得到e 标准差的估计值1213.446935.1946)(==e S对于给定的显著性水平05.0=α,查出自由度15=ν的t 分布双侧分位数13.2)15(2/05.0=t 得到Y 置信度为95%的预测区间为)6718.2040,18527151()1213.4413.26935.1946,1213.4413.26935.1946()()(),()(2/^2/^=⨯+⨯-=⎪⎭⎫ ⎝⎛⋅+⋅-e S t Y e S t Y νναα(6)解:321^150667.0933351.2919472.043078.0X X X Y +++=(一) 经济意义检验 919472.0^1=β表示农产品的销售量每增加1万担,收购量增加0.919472万担; 933351.2^1=β表示农产品的出口量每增加1万担,收购量增加2.9333351万担; 150667.0^1=β表示农产品的库存量每增加1万担,收购量增加0.150667万担;(二) 统计检验1. 拟合优度检验554193.0600311.022==R R ， 2. F 检验提出检验的原假设为0:210==ββH得F 统计量为：F-statistic=13.01685对于给定的显著性水平05.0=α，查出自由度26=ν的F 分布98.2)263(05.0=，F .因为F=13.01685>2.98，所以否定0H ,总体回归方程是显著的，即农产品的销售量与出口量、库存量和收购量之间存在显著的线性关系。

3.2解答：（1）因为自由度df=n-1=14,则样本容量n=15因为有 总变差平方和=参差平方和+回归平方和 ，即TSS=RSS+ESS 则残差平方和RSS=TSS-ESS=66042-65965=77因为有两个解释变量2X 和3X ，则k=3，回归平方和ESS 的自由度为：df=k-1=3-1=2 残差平方和RSS 的自由度为：df=n-k=15-3=12 （2）模型的可决系数为：2659650.99883466042ESS R TSS === 调整后的修正可决系数为：22221111i i e n n R R n k y n k--=-=---∑∑ 15110.9988340.9986153-=-⨯=- （3）从模型的可决系数20.998834R =及修正可决系数20.9986R =可以说明整个模型可以较好的解释被解释变量，即两个解释变量2X 和.3X 联合起来对被解释变量有很显著的影响，但是这并不能确定两个解释变量2X 和.3X 各自对Y 都有显著影响。

要确定每个变量分别对Y 的影响，需要做回归参数的显著性检验（t 检验）。

3.4解答：（１）．建立的模型为t t t t u X X Y +++=33221βββ 经过EViews 软件的处理，可以得到回归分析报告：Dependent Variable: Y Method: Least Squares Date: 03/14/12 Time: 21:32 Sample: 1970 1982 Included observations: 13Variable Coefficient Std. Error t-Statistic Prob. C 7.105975 1.618555 4.390321 0.0014 X2 -1.393115 0.310050 -4.493196 0.0012 R-squared0.872759 Mean dependent var 7.756923 Adjusted R-squared 0.847311 S.D. dependent var 3.041892 S.E. of regression 1.188632 Akaike info criterion 3.382658 Sum squared resid 14.12846 Schwarz criterion 3.513031 Log likelihood -18.98728 F-statistic 34.29559 Durbin-Watson stat2.254851 Prob(F-statistic)0.000033则该模型的估计为：23tˆ7.105975+-1.393115X 1.480674X t t Y =+ 经济学的说明：实际通货膨胀率受到失业率和预期通货膨胀率的共同影响，在预期通货膨胀率不变的前提下，失业率每提高1%，实际通货膨胀率就会平均下降1.393115%；在失业率不变的前提下，预期通货膨胀率每提高1%，实际通货膨胀率就会升高1.480674%。

第三章练习题及参考解答欧阳光明（2021.03.07）3.1为研究中国各地区入境旅游状况，建立了各省市旅游外汇收入（Y ，百万美元）、旅行社职工人数（X1，人）、国际旅游人数（X2，万人次）的模型，用某年31个省市的截面数据估计结果如下：t=(3.066806) (6.652983) (3.378064)R2=0.934331 92964.02=R F=191.1894 n=311)从经济意义上考察估计模型的合理性。

2)在5%显著性水平上，辨别检验参数21,ββ的显著性。

3)在5%显著性水平上，检验模型的整体显著性。

练习题3.1参考解答:(1)由模型估计结果可看出：从经济意义上说明，旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。

平均说来，旅行社职工人数增加1人，旅游外汇收入将增加0.1179百万美元；国际旅游人数增加1万人次，旅游外汇收入增加1.5452百万美元。

这与经济理论及经验合适，是合理的。

（2）取05.0=α，查表得048.2)331(025.0=-t因为3个参数t 统计量的绝对值均年夜于048.2)331(025.0=-t ，说明经t 检验3个参数均显著不为0，即旅行社职工人数和国际旅游人数辨别对旅游外汇收入都有显著影响。

（3）取05.0=α，查表得34.3)28,2(05.0=F ，由于34.3)28,2(1894.19905.0=>=F F ，说明旅行社职工人数和国际旅游人数联合起来对旅游外汇收入有显著影响，线性回归方程显著成立。

3.2 表3.6给出了有两个解释变量2X 和.3X 的回归模型方差阐发的部分结果：3.6 方差阐发表1）回归模型估计结果的样本容量n 、残差平方和RSS 、回归平方和ESS 与残差平方和RSS 的自由度各为几多?2）此模型的可决系数和调整的可决系数为几多?3）利用此结果能对模型的检验得出什么结论?能否确定两个解释变量2X 和.3X 各自对Y 都有显著影响? 练习题3.2参考解答:(1) 因为总变差的自由度为14=n1，所以样本容量：n=14+1=15因为 TSS=RSS+ESS 残差平方和RSS=TSSESS=6604265965=77 回归平方和的自由度为：k1=31=2残差平方和RSS 的自由度为：nk=153=12（2）可决系数为：2659650.99883466042ES R TSS S === 修正的可决系数：222115177110.998615366042i i e n R n k y --=-=-⨯=--∑∑ （3）这说明两个解释变量2X 和.3X 联合起来对被解释变量有很显著的影响，可是还不克不及确定两个解释变量2X 和.3X 各自对Y 都有显著影响。

第三章练习题及参考解答3.1为研究中国各地区入境旅游状况，建立了各省市旅游外汇收入（Y ，百万美元）、旅行社职工人数（X1，人）、国际旅游人数（X2，万人次）的模型，用某年31个省市的截面数据估计结果如下：t=(3.066806) (6.652983) (3.378064) R2=0.93433192964.02=R F=191.1894 n=311)从经济意义上考察估计模型的合理性。

2)在5%显著性水平上，辨别检验参数21,ββ的显著性。

3)在5%显著性水平上，检验模型的整体显著性。

练习题3.1参考解答:(1)由模型估计结果可看出：从经济意义上说明，旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。

平均说来，旅行社职工人数增加1人，旅游外汇收入将增加0.1179百万美元；国际旅游人数增加1万人次，旅游外汇收入增加1.5452百万美元。

这与经济理论及经验合适，是合理的。

（2）取05.0=α，查表得048.2)331(025.0=-t因为3个参数t 统计量的绝对值均年夜于048.2)331(025.0=-t ，说明经t 检验3个参数均显著不为0，即旅行社职工人数和国际旅游人数辨别对旅游外汇收入都有显著影响。

（3）取05.0=α，查表得34.3)28,2(05.0=F ，由于34.3)28,2(1894.19905.0=>=F F ，说明旅行社职工人数和国际旅游人数联合起来对旅游外汇收入有显著影响，线性回归方程显著成立。

3.2 表3.6给出了有两个解释变量2X 和.3X 的回归模型方差阐发的部分结果：3.6 方差阐发表1）回归模型估计结果的样本容量n 、残差平方和RSS 、回归平方和ESS 与残差平方和RSS 的自由度各为几多?2）此模型的可决系数和调整的可决系数为几多?3）利用此结果能对模型的检验得出什么结论?能否确定两个解释变量2X 和.3X 各自对Y 都有显著影响? 练习题3.2参考解答:(1) 因为总变差的自由度为14=n1，所以样本容量：n=14+1=15 因为TSS=RSS+ESS残差平方和RSS=TSSESS=6604265965=77回归平方和的自由度为：k1=31=2残差平方和RSS 的自由度为：nk=153=12（2）可决系数为：2659650.99883466042ES R TSSS ===修正的可决系数：222115177110.998615366042i i e n R n k y --=-=-⨯=--∑∑（3）这说明两个解释变量2X 和.3X 联合起来对被解释变量有很显著的影响，可是还不克不及确定两个解释变量2X 和.3X 各自对Y 都有显著影响。

第三章 多元线性回归模型一、单项选择题1、决定系数2R 是指【 】A 剩余平方和占总离差平方和的比重B 总离差平方和占回归平方和的比重C 回归平方和占总离差平方和的比重D 回归平方和占剩余平方和的比重2、在由n=30的一组样本估计的、包含3个解释变量的线性回归模型中，计算的多重决定系数为0.8500，则调整后的决定系数为【 】A 0.8603B 0.8389C 0.8 655D 0.83273、设k 为模型中的参数个数，则回归平方和是指【 】 A 21)(Y Yn i i -∑= B 21)ˆ(in i i Y Y -∑= C 21)ˆ(Y Y n i i-∑= D )1/()(21--∑=k Y Y n i i4、下列样本模型中，哪一个模型通常是无效的【 】A i C （消费）＝500＋0.8i I （收入）B d i Q （商品需求）＝10＋0.8i I （收入）＋0.9i P （价格）C s i Q （商品供给）＝20＋0.75i P （价格）D i Y （产出量）＝0.656.0i L （劳动）4.0iK （资本） 5、对于iki k i i i e X X X Y +++++=ββββˆˆˆˆ22110 ，统计量∑∑----)1/()ˆ(/)ˆ(22k n Y Y k Y Y i i i 服从【 】 A t(n-k) B t(n-k-1) C F(k-1,n-k) D F(k,n-k-1)6、对于iki k i i i e X X X Y +++++=ββββˆˆˆˆ22110 ，检验H 0:0=i β),,1,0(k i =时，所用的统计量)ˆvar(ˆi it ββ=服从【 】A t(n-k-1)B t(n-k-2)C t(n-k+1)D t(n-k+2)7、调整的判定系数 与多重判定系数 之间有如下关系【 】A 1122---=k n n R RB 11122----=k n n R R C 11)1(122---+-=k n n R R D 11)1(122-----=k n n R R 8、用一组有30 个观测值的样本估计模型i i i i u X X Y +++=22110βββ后，在0.05的显著性水平下对的显著性作t 检验，则1β显著地不等于零的条件是其统计量t 大于【 】 A 05.0t （30） B 025.0t （28） C （27） D 025.0F （1，28）9、如果两个经济变量X 与Y 间的关系近似地表现为当X 发生一个绝对量变动（∆X ）时，Y 有一个固定地相对量（∆Y/Y ）变动，则适宜配合的回归模型是【 】A i i i u X Y ++=10ββB ln i i i u X Y ++=10ββC i ii u X Y ++=110ββ D ln i i i u X Y ++=ln 10ββ 10、对于iki k i i i e X X X Y +++++=ββββˆˆˆˆ22110 ，如果原模型满足线性模型的基本假设，则在零假设j β＝0下，统计量)ˆ(/ˆjj s ββ（其中s(j β)是j β的标准误差）服从【 】 A t （n-k ） B t (n-k-1) C F （k-1，n-k ） D F （k ，n-k-1）11、下列哪个模型为常数弹性模型【 】A ln i i i u X Y ++=ln ln 10ββB ln i i i u X Y ++=10ln ββC i i i u X Y ++=ln 10ββD i ii u X Y ++=110ββ 12、模型i i i u X Y ++=ln 10ββ中，Y 关于X 的弹性为【 】1β025.0tA iX 1β B i X 1β C i Y 1β D i Y 1β 13、模型ln i i i u X Y ++=ln ln 10ββ中，的实际含义是【 】A X 关于Y 的弹性B Y 关于X 的弹性C X 关于Y 的边际倾向D Y 关于X 的边际倾向14、关于经济计量模型进行预测出现误差的原因，正确的说法是【 】A.只有随机因素B.只有系统因素C.既有随机因素，又有系统因素D.A 、B 、C 都不对15、在多元线性回归模型中对样本容量的基本要求是(k 为解释变量个数)：【 】A n ≥k+1B n<k+1C n ≥30或n ≥3（k+1）D n ≥3016、用一组有30个观测值的样本估计模型i i i i u X X Y +++=22110βββi ，并在0.05的显著性水平下对总体显著性作F 检验，则检验拒绝零假设的条件是统计量F 大于【 】A F 0.05(3,30)B F 0.025(3,30)C F 0.05(2,27)D F 0.025(2,27)17、对小样本回归系数进行检验时，所用统计量是( )A 正态统计量B t 统计量C χ2统计量D F 统计量18、在多元回归中，调整后的判定系数2R 与判定系数2R 的关系有【 】A 2R <2RB 2R >2RC 2R =2RD 2R 与2R 的关系不能确定 19、根据判定系数2R 与F 统计量的关系可知，当2R ＝1时有【 】A F ＝－1B F ＝0C F ＝1D F ＝∞20、回归分析中，用来说明拟合优度的统计量为【 】A 相关系数B 判定系数C 回归系数D 标准差21、对于二元线性回归模型的总体显著性检验的F 统计量，正确的是【 】。

第三章
多元线性回归模型
第一部分 练习题
计算题 考虑以下方程（括号内为估计标准差） 1
8.5620.3640.004t t t S P P -=++ （0.080） （0.072）
n =19，2R =0.873；
其中：S =t 年的销售量
P t =年的广告费用
请回答下列问题：
（1）对销售量估计的斜率系数进行假设检验。

（2）讨论1t P -在理论上是否正确，对本模型的正确性进行讨论。

1t P -是否应从方程中删除？为什么？
第二部分 参考答案
计算题
（2）由于1t P -不显著，可以将其从方程中删去，此时由于时滞短了一年，主成分可能正确，但时滞长度不正确。

在这样的情况下，利用同样的数据检验许多不同的时滞，可能不是个好方法，但如果可以建立另外一个数据集，这样检验也许是有用的。

2011年各地区的百户拥有家用汽车■等效据第三章习题 3.1地区 百户拥有家用汽车量Y/辆人均GDPX2/万元城慎人口比复X3/*交通工具消费价格指数X4 （上年=100）北京 37.71 8.05 S6. 20 95. 92 天津 20. 62 & 31 80. 50 103. 57 河北 23. 32 3. 39 15. 60 99. 03 山西 18. 60 3.13 19. 68 98. 96 内蒙 古 19. 625. 7956. 6299.11辽宁 11.15 5.07 64.05 100. 12 吉林 11. 24 3.81 53.40 97.15 黑龙 江 5.293.2856. 50100. 54上海 18. 15 8・18 S9. 30 101.58 江苏 23. 92 6.22 61.90 9& 95 浙江 33. 85 5.92 62. 30 96. 69 安徽 9. 20 2.56 44.80 100. 25 福建 17. 83 1. 72 5& 10 100. 75 江西 8.88 2.61 45.70 100. 91 山东28.12 1. 71 50. 95 98. 501-1. 062.87 10. 57 100. 59 湖北 9. 693. 41 51.83 101.15 湖南 12. 82 2.98 15.10 100. 02 广东 30.71 5.07 66. 50 97. 55 广西 17. 24 2. 52 41.80 102.28 海南15. 82 2.88 50. 50 102.0610. 143. 43 55.02 99.12 四川 12. 25 2.61 41. 83 99. 76 贵州 10. 18 1・64 34.96 100. 71 云南 23. 32 1.92 36. 80 96. 25 西藏 25. 302.00 22.71 99. 95 陕西19 9?3. 31 17. 30 101. 597. 331.96 37.15 100. 51 青海 6. 082.94 16. 22 100. 16 宁夏12. 40 3.29 49.82 100. 99 新9112. 322.9943. 51100. 97一、 研究的目的和要求经济增长，公共服务、市场价格、交通状况，社会环境、政策因素都会影响中国汽车拥有量。