高级计量经济学课后习题参考解答

课后习题参考答案第二章教材习题与解析1、 判断下列表达式是否正确：y i =β0+β1x i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i ,i =1,2,⋯nE(y i |x i )=β0+β1x i +u i ,i =1,2,⋯n E(y i |x i )=β0+β1x i ,i =1,2,⋯nE(y i |x i )=β̂0+β̂1x i ,i =1,2,⋯ny i =β0+β1x i +u i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n y ̂i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n答案：对于计量经济学模型有两种类型，一是总体回归模型，另一是样本回归模型。

两类回归模型都具有确定形式与随机形式两种表达方式：总体回归模型的确定形式：X X Y E 10)|(ββ+= 总体回归模型的随机形式：μββ++=X Y 10样本回归模型的确定形式：X Y 10ˆˆˆββ+= 样本回归模型的随机形式：e X Y ++=10ˆˆββ 除此之外，其他的表达形式均是错误的2、给定一元线性回归模型：y =β0+β1x +u （1）叙述模型的基本假定；（2）写出参数β0和β1的最小二乘估计公式；（3）说明满足基本假定的最小二乘估计量的统计性质； （4）写出随机扰动项方差的无偏估计公式。

答案：（1）线性回归模型的基本假设有两大类，一类是关于随机误差项的，包括零均值、同方差、不序列相关、满足正态分布等假设；另一类是关于解释变量的，主要是解释变量是非随机的，如果是随机变量，则与随机误差项不相关。

（2）12ˆi iix yxβ=∑∑，01ˆˆY X ββ=- （3）考察总体的估计量，可从如下几个方面考察其优劣性：1）线性性，即它是否是另一个随机变量的线性函数； 2）无偏性，即它的均值或期望是否等于总体的真实值；3）有效值，即它是否在所有线性无偏估计量中具有最小方差；4）渐进无偏性，即样本容量趋于无穷大时，它的均值序列是否趋于总体真值； 5）一致性，即样本容量趋于无穷大时，它是否依概率收敛于总体的真值；6）渐进有效性，即样本容量趋于无穷大时，它在所有的一致估计量中是否具有最小的渐进方差。

第十三章面板数据模型一简单题1、简述面板数据模型的优点和局限性它能综合利用样本信息，同时反映应变量在截面和时序两个方向上的变化规律及特征。

由于面板数据模型在经济定量分析中，起着只用截面或只用时序数据模型不可替代的独特优点，而具有很高的应用价值。

总之：1．增加了样本容量；2. 可多层面分析经济问题局限性：模型设定错误与数据手机不慎引起较大的偏差；研究截面或者平行数据时，由于样本非随机性造成观测值的偏差，从而导致模型选择上的偏差。

2、你是如何理解面板数据的？在经济领域中，同时具有截面与时序特征的数据很多。

如统计年鉴中提供的各地区或各国的若干系列的年度（季度或月度）经济总量数据；在企业投资分析中，要用到多个企业若干指标的月度或季度时间序列数据；在城镇居民消费分析中，要用到不同省市反映居民消费和收入的年度时序数据。

我们将上述的企业、或地区等统称为个体，从行的方向看，是由若干个体在某个时期构成的截面观察值（截面样本），从列的方向看，是各时间序列。

这种具有三维（截面、时期、变量）信息的数据结构称为面板。

这是“面板”数据的由来，面板数据也称为时序截面数据或混合数据（Pooled Data）。

3、简述建立面板数据模型的过程。

（1）建立面板数据对象，即建立工作文件；（2）面板时序变量平稳性检验；（3）协整检验；（4）模型识别；（5）建立模型；（6）结论。

二填空题1、GDP界面变量是一维变量，面板变量为三维变量。

2、面板数据模型是无斜率系数非齐性、而截距齐性的模型。

3、面板数据模型识别包括效应模型识别和具体模型识别。

4、建立面板数据模型之前，要对面板变量进行平稳性检验和协整检验。

第十二章向量自回归(VAR)模型和向量误差修正(VEC)模型一简答题1、VAR模型的特点VAR模型不以经济理论为指导，它根据样本数据统计特征建模。

VAR模型对参数不施加零约束（如t检验），故称其为无约束VAR模型。

VAR模型的解释变量中不含t期变量，所有与线性联利方程组模型有关的问题均不存在。

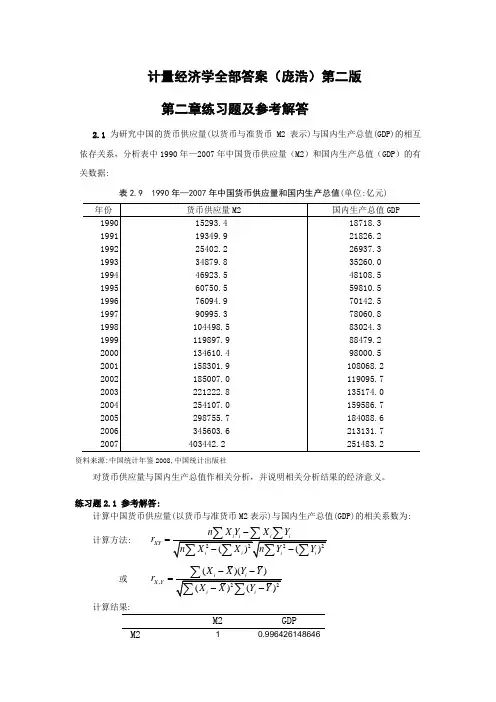
计量经济学全部答案（庞浩）第二版 第二章练习题及参考解答2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系，分析表中1990年—2007年中国货币供应量（M2）和国内生产总值（GDP ）的有关数据:表2.9 1990年—2007年中国货币供应量和国内生产总值(单位:亿元)资料来源:中国统计年鉴2008,中国统计出版社对货币供应量与国内生产总值作相关分析，并说明相关分析结果的经济意义。

练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或 ,()()X Y X X Y Y r --=计算结果:M2GDPM210.996426148646GDP 0.996426148646 1经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。

2.2 为研究美国软饮料公司的广告费用X与销售数量Y的关系,分析七种主要品牌软饮料公司的有关数据表2.10 美国软饮料公司广告费用与销售数量资料来源:(美) Anderson D R等. 商务与经济统计.机械工业出版社.1998. 405绘制美国软饮料公司广告费用与销售数量的相关图, 并计算相关系数，分析其相关程度。

能否在此基础上建立回归模型作回归分析？练习题2.2参考解答美国软饮料公司的广告费用X与销售数量Y的散点图为说明美国软饮料公司的广告费用X与销售数量Y正线性相关。

若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。

回归结果表明，广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。

计量经济学（第四版）习题参考答案第一章 绪论1.1 一般说来，计量经济分析按照以下步骤进行：（1）陈述理论（或假说） （2）建立计量经济模型 （3）收集数据 （4）估计参数 （5）假设检验 （6）预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量，但它（它们）仅是影响因变量的主要因素，还有很多对因变量有影响的因素，它们相对而言不那么重要，因而未被包括在模型中。

为了使模型更现实，我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素，这些因素包括相对而言不重要因而未被引入模型的变量，以及纯粹的随机因素。

1.3时间序列数据是按时间周期（即按固定的时间间隔）收集的数据，如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。

横截面数据是在同一时点收集的不同个体（如个人、公司、国家等）的数据。

如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。

1.4 估计量是指一个公式或方法，它告诉人们怎样用手中样本所提供的信息去估计总体参数。

在一项应用中，依据估计量算出的一个具体的数值，称为估计值。

如Y 就是一个估计量，1nii YY n==∑。

现有一样本，共4个数，100，104，96，130，则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。

第二章 计量经济分析的统计学基础2.1 略，参考教材。

2.2 NS S x ==45=1.25 用α=0.05，N-1=15个自由度查表得005.0t =2.947，故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说，根据样本，我们有99%的把握说，北京男高中生的平均身高在170.316至177.684厘米之间。

2.3 原假设 120:0=μH备择假设 120:1≠μH检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。

计量经济学习题参考答案第⼀章导论1．计量经济学是⼀门什么样的学科？答：计量经济学的英⽂单词是Econometrics，本意是“经济计量”，研究经济问题的计量⽅法，因此有时也译为“经济计量学”。

将Econometrics译为“计量经济学”是为了强调它是现代经济学的⼀门分⽀学科，不仅要研究经济问题的计量⽅法，还要研究经济问题发展变化的数量规律。

可以认为，计量经济学是以经济理论为指导，以经济数据为依据，以数学、统计⽅法为⼿段，通过建⽴、估计、检验经济模型，揭⽰客观经济活动中存在的随机因果关系的⼀门应⽤经济学的分⽀学科。

2．计量经济学与经济理论、数学、统计学的联系和区别是什么？答：计量经济学是经济理论、数学、统计学的结合，是经济学、数学、统计学的交叉学科（或边缘学科）。

计量经济学与经济学、数学、统计学的联系主要是计量经济学对这些学科的应⽤。

计量经济学对经济学的应⽤主要体现在以下⼏个⽅⾯：第⼀，计量经济学模型的选择和确定，包括对变量和经济模型的选择，需要经济学理论提供依据和思路；第⼆，计量经济分析中对经济模型的修改和调整，如改变函数形式、增减变量等，需要有经济理论的指导和把握；第三，计量经济分析结果的解读和应⽤也需要经济理论提供基础、背景和思路。

计量经济学对统计学的应⽤，⾄少有两个重要⽅⾯：⼀是计量经济分析所采⽤的数据的收集与处理、参数的估计等，需要使⽤统计学的⽅法和技术来完成；⼀是参数估计值、模型的预测结果的可靠性，需要使⽤统计⽅法加以分析、判断。

计量经济学对数学的应⽤也是多⽅⾯的，⾸先，对⾮线性函数进⾏线性转化的⽅法和技巧，是数学在计量经济学中的应⽤；其次，任何的参数估计归根结底都是数学运算，较复杂的参数估计⽅法，或者较复杂的模型的参数估计，更需要相当的数学知识和数学运算能⼒，另外，在计量经济理论和⽅法的研究⽅⾯，需要⽤到许多的数学知识和原理。

计量经济学与经济学、数学、统计学的区别也很明显，经济学、数学、统计学中的任何⼀门学科，都不能替代计量经济学，这三门学科简单地合起来，也不能替代计量经济学。

第一章绪论一、填空题：1．计量经济学是以揭示经济活动中客观存在的__________为内容的分支学科，挪威经济学家弗里希，将计量经济学定义为__________、__________、__________三者的结合。

2．数理经济模型揭示经济活动中各个因素之间的__________关系，用__________性的数学方程加以描述，计量经济模型揭示经济活动中各因素之间__________的关系，用__________性的数学方程加以描述。

3．经济数学模型是用__________描述经济活动。

4．计量经济学根据研究对象和内容侧重面不同，可以分为__________计量经济学和__________计量经济学。

5．计量经济学模型包括__________和__________两大类。

6．建模过程中理论模型的设计主要包括三部分工作，即__________、____________________、____________________。

7．确定理论模型中所包含的变量，主要指确定__________。

8．可以作为解释变量的几类变量有__________变量、__________变量、__________变量和__________变量。

9．选择模型数学形式的主要依据是__________。

10．研究经济问题时，一般要处理三种类型的数据：__________数据、__________数据和__________数据。

11．样本数据的质量包括四个方面__________、__________、__________、__________。

12．模型参数的估计包括__________、__________和软件的应用等内容。

13．计量经济学模型用于预测前必须通过的检验分别是__________检验、__________检验、__________检验和__________检验。

14．计量经济模型的计量经济检验通常包括随机误差项的__________检验、__________检验、解释变量的__________检验。

2.7 设销售收入,,,,,,,,,12个月的有关资料计算出以下数据：（单位：万元） 2()425053.73tXX -=∑ 647.88X = 2()262855.25tY Y -=∑ 549.8Y =()()334229.09tt XX Y Y --=∑（1） 拟合简单线性回归方程，并对方程中回归系数的经济意义作出解释。

（2） 计算可决系数和回归估计的标准误差。

（3） 对2β进行显著水平为5%的显著性检验。

（4） 假定下年1月销售收入为800万元，利用拟合的回归方程预测其销售成本，并给出置信度为95%的预测区间。

练习题2.7参考解答：(1)建立回归模型: i i i u X Y ++=21ββ用OLS 法估计参数: 222()()334229.09ˆ0.7863()425053.73ii i iiiX X Y Y x yX X xβ--====-∑∑∑∑12ˆˆ549.80.7863647.8866.2872Y X ββ=-=-⨯= 估计结果为: ˆ66.28720.7863i iY X =+ 说明该百货公司销售收入每增加1元,平均说来销售成本将增加0.7863元。

(2)计算可决系数和回归估计的标准误差 可决系数为：22222222222ˆˆˆ()0.7863425053.73262796.990.999778262855.25262855.25i i iiiiy x x Ryyyββ===⨯===∑∑∑∑∑∑由 2221i iery=-∑∑ 可得222(1)ii eR y =-∑∑222(1)(10.999778)262855.2558.3539ii eR y =-=-⨯=∑∑回归估计的标准误差: ˆ 2.4157σ=(3) 对2β进行显著水平为5%的显著性检验*222^^22ˆˆ~(2)ˆˆ()()t t n SE SE βββββ-==-^22.4157ˆ()0.0037651.9614SE β==== *2^2ˆ0.7863212.51350.0037ˆ()t SE ββ===查表得 0.05α=时,0.025(122) 2.228t -=<*212.5135t =表明2β显著不为0,销售收入对销售成本有显著影响.(4) 假定下年1月销售收入为800万元，利用拟合的回归方程预测其销售成本，并给出置信度为95%的预测区间。

计量经济学各章习题第一章绪论1.1试列出计量经济分析地主要步骤.1.2计量经济模型中为何要包括扰动项?1.3什么是时间序列和横截面数据? 试举例说明二者地区别1.4估计量和估计值有何区别？第二章计量经济分析地统计学基础2.1名词解释随机变量概率密度函数抽样分布样本均值样本方差协方差相关系数标准差标准误差显著性水平置信区间无偏性有效性一致估计量接受域拒绝域第I 类错误2.2请用例 2.2中地数据求北京男生平均身高地99％置信区间.2.325 个雇员地随机样本地平均周薪为130元，试问此样本是否取自一个均值为120 元、标准差为10 元地正态总体？文档收集自网络，仅用于个人学习2.4某月对零售商店地调查结果表明，市郊食品店地月平均销售额为2500 元，在下一个月份中，取出16 个这种食品店地一个样本，其月平均销售额为2600 元，销售额地标准差为480 元.试问能否得出结论，从上次调查以来，平均月销售额已经发生了变化？文档收集自网络，仅用于个人学习第三章双变量线性回归模型3.1判断题（判断对错；如果错误，说明理由）（1）OLS 法是使残差平方和最小化地估计方法.（2）计算OLS 估计值无需古典线性回归模型地基本假定.（3）若线性回归模型满足假设条件（1）～（4），但扰动项不服从正态分布，则尽管OLS 估计量不再是BLUE ，但仍为无偏估计量.文档收集自网络，仅用于个人学习（4）最小二乘斜率系数地假设检验所依据地是t 分布，要求地抽样分布是正态分布.2（5）R2＝TSS/ESS.（6）若回归模型中无截距项，则.（7）若原假设未被拒绝，则它为真.（8）在双变量回归中，地值越大，斜率系数地方差越大.3.2设和分别表示Y 对X 和X 对Y 地OLS 回归中地斜率，证明r 为X 和Y 地相关系数.3.3证明：（1）Y 地真实值与OLS 拟合值有共同地均值，即；（2）OLS 残差与拟合值不相关，即.3.4证明本章中（ 3.18）和（ 3.19）两式：（1）（2）3.5考虑下列双变量模型：模型1：模型2：（1）1 和1地OLS 估计量相同吗？它们地方差相等吗？（2）2 和2地OLS 估计量相同吗？它们地方差相等吗？3.6有人使用1980－1994 年度数据，研究汇率和相对价格地关系，得到如下结果：其中，Y＝马克对美元地汇率X＝美、德两国消费者价格指数（CPI）之比，代表两国地相对价格（1）请解释回归系数地含义；（2）X t 地系数为负值有经济意义吗？（3）如果我们重新定义X 为德国CPI与美国CPI之比，X 地符号会变化吗？为什么？3.7随机调查200 位男性地身高和体重，并用体重对身高进行回归，结果如下：其中Weight 地单位是磅（lb ），Height 地单位是厘米（cm）.（1）当身高分别为177.67cm、164.98cm、187.82cm 时，对应地体重地拟合值为多少？（2）假设在一年中某人身高增高了 3.81cm，此人体重增加了多少？3.8设有10 名工人地数据如下：X 10 7 10 5 8 8 6 7 9 10Y 11 10 12 6 10 7 9 10 11 10 其中X= 劳动工时，Y= 产量（1）试估计Y=α+βX + u（要求列出计算表格）；（2）提供回归结果（按标准格式）并适当说明；（3）检验原假设β=1.0.3.9用12 对观测值估计出地消费函数为Y=10.0+0.90X ，且已知=0.01，=200，=4000，试预测当X=250 时Y 地值，并求Y 地95%置信区间.文档收集自网络，仅用于个人学习3.10设有某变量（Y）和变量（X）1995—1999 年地数据如下:（3）试预测X=10 时Y 地值，并求Y 地95%置信区间.3.11根据上题地数据及回归结果，现有一对新观测值X ＝20，Y＝7.62，试问它们是否可能来自产生样本数据地同一总体？文档收集自网络，仅用于个人学习3.12有人估计消费函数，得到如下结果（括号中数字为t 值）：＝15 + 0.81 ＝0.98（2.7）（6.5）n=19（1）检验原假设：＝0（取显著性水平为5％）（2）计算参数估计值地标准误差；（3）求地95％置信区间，这个区间包括0 吗？3.13试用中国1985—2003 年实际数据估计消费函数：=α+β + u t其中：C代表消费，Y 代表收入.原始数据如下表所示，表中：Cr＝农村居民人均消费支出（元）Cu＝城镇居民人均消费支出（元）Y ＝国内居民家庭人均纯收入（元） Yr ＝农村居民家庭人均纯收入（元） Yu＝城镇居民家庭人均可支配收入（元） Rpop＝农村人口比重（%） pop＝历年年底我国人口总数（亿人）P＝居民消费价格指数（1985=100）Pr＝农村居民消费价格指数（1985=100）Pu＝城镇居民消费价格指数（1985=100）数据来源：《中国统计年鉴2004》使用计量经济软件，用国内居民人均消费、农村居民人均消费和城镇居民人均消费分别对各自地人均收入进行回归，给出标准格式回归结果；并由回归结果分析我国城乡居民消费行为有何不同.文档收集自网络，仅用于个人学习第四章多元线性回归模型4.1某经济学家试图解释某一变量Y 地变动.他收集了Y 和 5 个可能地解释变量～地观测值(共10 组)，然后分别作三个回归，结果如下(括号中数字为t 统计量)：文档收集自网络，仅用于个人学习( 1) = 51.5 + 3.21 R=0.63(3.45) (5.21)2) 33.43 + 3.67 + 4.62 + 1.21 R=0.75 文档收集自网络，仅用于个人学(3.61 )(2.56)(0.81) (0.22)3) 23.21 + 3.82 + 2.32 + 0.82 + 4.10 + 1.21(2.21 )(2.83)(0.62) (0.12) (2.10) (1.11)文档收集自网络，仅用于个人学习R=0.80 你认为应采用哪一个结果？为什么？4.2为研究旅馆地投资问题，我们收集了某地地1987-1995 年地数据来估计收益生产函数R=ALKe ，其中R=旅馆年净收益(万年) ，L=土地投入，K=资金投入， e 为自然对数地底.设回归结果如下(括号内数字为标准误差) ：文档收集自网络，仅用于个人学习= -0.9175 + 0.273lnL + 0.733lnK R=0.94(0.212) (0.135) (0.125)(1)请对回归结果作必要说明；( 2)分别检验α和β 地显著性；( 3)检验原假设：α =β = 0；4.3我们有某地1970-1987 年间人均储蓄和收入地数据，用以研究1970－1978 和1978 年以后储蓄和收入之间地关系是否发生显著变化. 引入虚拟变量后，估计结果如下(括号内数据为标准差) ：文档收集自网络，仅用于个人学习= -1.7502 + 1.4839D + 0.1504 - 0.1034D·R=0.9425 文档收集自网络，仅用于个人学习(0.3319) (0.4704) (0.0163) (0.0332)其中：Y=人均储蓄，X=人均收入，D= 请检验两时期是否有显著地结构性变化.4.4说明下列模型中变量是否呈线性，系数是否呈线性，并将能线性化地模型线性化.（1）（2）（3）4.5有学者根据某国19年地数据得到下面地回归结果：其中：Y=进口量（百万美元），X1 =个人消费支出（百万美元），X2 =进口价格/国内价格.（1）解释截距项以及X1和X2系数地意义；（2）Y 地总变差中被回归方程解释地部分、未被回归方程解释地部分各是多少？（3）进行回归方程地显著性检验,并解释检验结果；（4）对“斜率”系数进行显著性检验,并解释检验结果.4.6由美国46个州1992年地数据，Baltagi 得到如下回归结果：其中，C＝香烟消费（包/人年），P＝每包香烟地实际价格Y＝人均实际可支配收入（1）香烟需求地价格弹性是多少？它是否统计上显著？若是，它是否统计上异于-1？（2）香烟需求地收入弹性是多少？它是否统计上显著？若不显著，原因是什么？（3）求出.4.7有学者从209 个公司地样本，得到如下回归结果（括号中数字为标准误差）：其中，Salary＝CEO 地薪金Sales＝公司年销售额roe＝股本收益率（％）ros＝公司股票收益请分析回归结果.4.8为了研究某国1970－1992 期间地人口增长率，某研究小组估计了下列模型：其中：Pop＝人口（百万人），t＝趋势变量，.（1）在模型 1 中，样本期该地地人口增长率是多少？（2）人口增长率在1978 年前后是否显著不同？如果不同，那么1972－1977和1978－1992 两时期中，人口增长率各是多少？文档收集自网络，仅用于个人学习4.9设回归方程为Y= β0+β1X1+β2X2+β3X3+ u, 试说明你将如何检验联合假设：β1= β2 和β3 = 1 .文档收集自网络，仅用于个人学习4.10下列情况应引入几个虚拟变量，如何表示？（1）企业规模：大型企业、中型企业、小型企业；（2）学历：小学、初中、高中、大学、研究生.4.11在经济发展发生转折时期，可以通过引入虚拟变量来表示这种变化.例如，研究进口消费品地数量Y 与国民收入X 地关系时，数据散点图显示1979 年前后明显不同.请写出引入虚拟变量地进口消费品线性回归方程.文档收集自网络，仅用于个人学习4.12柯布－道格拉斯生产函数其中：GDP=地区国内生产总值（亿元）K=资本形成总额（亿元）L= 就业人数（万人）P=商品零售价格指数（上年＝100）试根据中国2003 年各省数据估计此函数并分析结果.数据如下表所示第五章模型地建立与估计中地问题及对策5.1判断题（判断对错；如果错误，说明理由）（1）尽管存在严重多重共线性，普通最小二乘估计量仍然是最佳线性无偏估计量（BLUE ）.（2）如果分析地目地仅仅是为了预测，则多重共线性并无妨碍. （3）如果解释变量两两之间地相关系数都低，则一定不存在多重共线性. （4）如果存在异方差性，通常用地t 检验和 F 检验是无效地. （5）当存在自相关时，OLS 估计量既不是无偏地，又不是有效地.（6）消除一阶自相关地一阶差分变换法假定自相关系数必须等于 1. （7）模型中包含无关地解释变量，参数估计量会有偏，并且会增大估计量地方差，即增大误差.（8）多元回归中，如果全部“斜率”系数各自经t 检验都不显著，则R2值也高不了.（9）存在异方差地情况下，OLS 法总是高估系数估计量地标准误差.（10）如果一个具有非常数方差地解释变量被（不正确地）忽略了，那么OLS 残差将呈异方差性.5.2考虑带有随机扰动项地复利增长模型：Y 表示GDP，Y0是Y 地基期值，r 是样本期内地年均增长率，t 表示年份，t＝1978，⋯,2003.文档收集自网络，仅用于个人学习试问应如何估计GDP 在样本期内地年均增长率？5.3 检验下列情况下是否存在扰动项地自相关 .（1） DW=0.81，n=21，k=3（2）DW=2.25，n=15，k=2（3）DW=1.56，n=30，k=55.4有人建立了一个回归模型来研究我国县一级地教育支出：Y= β0+β1X1+β 2X2+β3X3+u其中：Y，X1，X2 和X3分别为所研究县份地教育支出、居民人均收入、学龄儿童人数和可以利用地各级政府教育拨款.文档收集自网络，仅用于个人学习他打算用遍布我国各省、市、自治区地100 个县地数据来估计上述模型.（1）所用数据是什么类型地数据？（2）能否采用OLS 法进行估计？为什么？（3）如不能采用OLS 法，你认为应采用什么方法？5.5试从下列回归结果分析存在问题及解决方法：（1）= 24.7747 + 0.9415 - 0.0424 R=0.9635SE：（6.7525）（0.8229）（0.0807）其中：Y=消费，X2=收入，X3=财产，且n=5000 （2）= 0.4529 - 0.0041t R=0.5284t：（-3.9606） DW=0.8252其中Y= 劳动在增加值中地份额，t=时间该估计结果是使用1949-1964 年度数据得到地.5.6工资模型：wi＝b0＋b1Si＋b2Ei＋b3Ai＋b4Ui＋ui其中Wi＝工资，Si＝学校教育年限，Ei＝工作年限，Ai＝年龄，Ui＝是否参加工会.在估计上述模型时，你觉得会出现什么问题？如何解决？5.7你想研究某行业中公司地销售量与其广告宣传费用之间地关系.你很清楚地知道该行业中有一半地公司比另一半公司大，你关心地是这种情况下，什么估计方法比较合理.假定大公司地扰动项方差是小公司扰动项方差地两倍.文档收集自网络，仅用于个人学习（1）若采用普通最小二乘法估计销售量对广告宣传费用地回归方程（假设广告宣传费是与误差项不相关地自变量），系数地估计量会是无偏地吗？是一致地吗？是有效地吗？文档收集自网络，仅用于个人学习（2）你会怎样修改你地估计方法以解决你地问题？（3）能否对原扰动项方差假设地正确性进行检验？5.8考虑下面地模型其中GNP＝国民生产总值，M ＝货币供给. （1）假设你有估计此模型地数据，你能成功地估计出模型地所有系数吗？说明理由.（2）如果不能，哪些系数可以估计？（3）如果从模型中去掉这一项，你对（1）中问题地答案会改变吗？（4）如果从模型中去掉这一项，你对（1）中问题地答案会改变吗？5.9采用美国制造业1899－1922年数据，Dougherty得到如下两个回归结果：（1）（2）其中：Y＝实际产出指数，K＝实际资本投入指数，L ＝实际劳动力投入指数，t＝时间趋势（1）回归式（1）中是否存在多重共线性？你是如何得知地？（2）回归式（1）中，logK 系数地预期符号是什么？回归结果符合先验预期吗？为什么会这样？（3）回归式（1）中，趋势变量在其中起什么作用？（4）估计回归式（2）背后地逻辑是什么？（5）如果（1）中存在多重共线性，那么（2）式是否减轻这个问题？你如何得知？（6）两个回归地R2可比吗？说明理由.5.10有人估计了下面地模型：其中：C＝私人消费支出，GNP＝国民生产总值，D＝国防支出假定，将（1）式转换成下式：使用1946－1975数据估计（1）、（2）两式，得到如下回归结果（括号中数字为标准误差）：1）关于异方差，模型估计者做出了什么样地假定？你认为他地依据是什么？2）比较两个回归结果.模型转换是否改进了结果？也就是说，是否减小了估计标准误差？说明理由.5.11设有下列数据：RSS1＝55，K ＝4，n1＝30RSS3＝140，K ＝4，n3＝30 请依据上述数据，用戈德佛尔德－匡特检验法进行异方差性检验（5％显著性水平）.5.12考虑模型（1）也就是说，扰动项服从AR （2）模式，其中是白噪声.请概述估计此模型所要采取地步骤.5.13对第 3 章练习题 3.13 所建立地三个消费模型地结果进行分析：是否存在序列相关问题？如果有，应如何解决？5.14为了研究中国农业总产值与有效灌溉面积、化肥施用量、农作物总播种面积、受灾面积地相互关系，选31 个省市2003 年地数据资料，如下表所示：文档收集自网络，仅用于个人学习表中：Y＝农业总产值（亿元，不包括林牧渔）X1＝有效灌溉面积（千公顷）X2＝化肥施用量（万吨）X23＝化肥施用量（公斤/亩）X3＝农作物总播种面积（千公顷）X4＝受灾面积（千公顷）（1）回归并根据计算机输出结果写出标准格式地回归结果；（2）模型是否存在问题？如果存在问题，是什么问题？如何解决？第六章动态经济模型：自回归模型和分布滞后模型6.1判断题（判断对错；如果错误，说明理由）（1）所有计量经济模型实质上都是动态模型.（2）如果分布滞后系数中，有地为正有地为负，则科克模型将没有多大用处. （3）若适应预期模型用OLS 估计，则估计量将有偏，但一致. （4）对于小样本，部分调整模型地OLS 估计量是有偏地.（5）若回归方程中既包含随机解释变量，扰动项又自相关，则采用工具变量法，将产生无偏且一致地估计量.（6）解释变量中包括滞后因变量地情况下，用德宾－沃森d 统计量来检测自相关是没有实际用处地.6.2用OLS 对科克模型、部分调整模型和适应预期模型分别进行回归时，得到地OLS 估计量会有什么样地性质？文档收集自网络，仅用于个人学习6.3简述科克分布和阿尔蒙多项式分布地区别.6.4考虑模型假设相关.要解决这个问题，我们采用以下工具变量法：首先用对和回归，得到地估计值，然后回归其中是第一步回归（对和回归）中得到地.（1）这个方法如何消除原模型中地相关？（2）与利维顿采用地方法相比，此方法有何优点？6.5设其中：M＝对实际现金余额地需求，Y*＝预期实际收入，R*＝预期通货膨胀率假设这些预期服从适应预期机制：其中和是调整系数，均位于0和1之间.（1）请将M t 用可观测量表示；（2）你预计会有什么估计问题？6.6考虑分布滞后模型假设可用二阶多项式表示诸如下：若施加约束＝＝0，你将如何估计诸系数（，i=0,1, (4)6.7为了研究设备利用对于通货膨胀地影响，T. A.吉延斯根据1971年到1988年地美国数据获得如下回归结果：文档收集自网络，仅用于个人学习其中：Y＝通货膨胀率（根据GNP 平减指数计算）X t＝制造业设备利用率X t－1 ＝滞后一年地设备利用率1）设备利用对于通货膨胀地短期影响是什么？长期影响又是什么？(2)每个斜率系数是统计显著地吗？(3)你是否会拒绝两个斜率系数同时为零地原假设？将利用何种检验？6.8考虑下面地模型：Y t = α+β(W0X t+ W1X t-1 + W2X t-2 + W3X t-3)+u t 请说明如何用阿尔蒙滞后方法来估计上述模型(设用二次多项式来近似) .6.9下面地模型是一个将部分调整和适应预期假说结合在一起地模型：Y t*= βX t+1eY t-Y t-1 = δ(Y t*- Y t-1) + u tX t+1e- X t e= (1-λ)( X t - X t e)；t=1，2，⋯， n式中Y t*是理想值，X t+1e和X t e是预期值.试推导出一个只包含可观测变量地方程，并说明该方程参数估计方面地问题.文档收集自网络，仅用于个人学习第七章时间序列分析7.1单项选择题（1）某一时间序列经一次差分变换成平稳时间序列，此时间序列称为（）地.A．1 阶单整B．2阶单整C．K 阶单整D．以上答案均不正确文档收集自网络，仅用于个人学习（2）如果两个变量都是一阶单整地，则（）.A ．这两个变量一定存在协整关系B．这两个变量一定不存在协整关系C．相应地误差修正模型一定成立D．还需对误差项进行检验文档收集自网络，仅用于个人学习（3）如果同阶单整地线性组合是平稳时间序列，则这些变量之间关系是（） .A. 伪回归关系B.协整关系C.短期均衡关系D. 短期非均衡关系（4）．若一个时间序列呈上升趋势，则这个时间序列是（）.A ．平稳时间序列B．非平稳时间序列C．一阶单整序列 D. 一阶协整序列7.2请说出平稳时间序列和非平稳时间序列地区别，并解释为什么在实证分析中确定经济时间序列地性质是十分必要地.文档收集自网络，仅用于个人学习7.3什么是单位根？7.4Dickey－Fuller（DF）检验和Engle－Granger（EG）检验是检验什么地？文档收集自网络，仅用于个人学习7.5什么是伪回归？在回归中使用非均衡时间序列时是否必定会造成伪回归？7.6由1948－1984 英国私人部门住宅开工数（X）数据，某学者得到下列回归结果：注：5％临界值值为-2.95，10％临界值值为-2.60. （1）根据这一结果，检验住宅开工数时间序列是否平稳.（2）如果你打算使用t 检验，则观测地t 值是否统计显著？据此你是否得出该序列平稳地结论？（3）现考虑下面地回归结果：请判断住宅开工数地平稳性.7.7由1971-I 到1988-IV 加拿大地数据，得到如下回归结果；A.B.C.其中，M1＝货币供给，GDP=国内生产总值，e t＝残差（回归A）（1）你怀疑回归 A 是伪回归吗？为什么？（2）回归 B 是伪回归吗？请说明理由.（3）从回归 C 地结果，你是否改变（1）中地结论，为什么？（4）现考虑以下回归：这个回归结果告诉你什么？这个结果是否对你决定回归 A 是否伪回归有帮助？7.8 检验我国人口时间序列地平稳性，数据区间为1949－2003 年.单位：万人7.9对中国进出口贸易进行协整分析，如果存在协整关系，则建立E CM 模型.1951－2003 年中国进口（im ）、出口（ex）和物价指数（pt，商品零售物价指数）时间序列数据见下表.因为该期间物价变化大，特别是改革开放以后变化更为激烈，所以物价指数也作为一个解释变量加入模型中.为消除物价变动对进出口数据地影响以及消除进出口数据中存在地异方差，定义三个变量如下：文档收集自网络，仅用于个人学习第八章联立方程模型8.1判断题（判断对错；如果错误，说明理由）（1）OLS 法适用于估计联立方程模型中地结构方程.（2）2SLS 法不能用于不可识别方程.（3）估计联立方程模型地2SLS 法和其它方法只有在大样本地情况下，才能具有我们期望地统计性质 .(4) 联立方程模型作为一个整体，不存在类似 R 2这样地拟合优度测度 .(5) 如果要估计地方程扰动项自相关或存在跨方程地相关， 则 2SLS 法和其它估 计结构方程地方法都不能用 .(6) 如果一个方程恰好识别，则 ILS 和 2SLS 给出相同结果 .8.2 单项选择题1) 结构式模型中地方程称为结构方程 .在结构方程中， 解释变量可以是前定变3) 如果联立方程模型中某个结构方程包含了模型中所有地变量，则这个方程5)当一个结构式方程为恰好识别时，这个方程中内生解释变量地个数( A ．与被排除在外地前定变量个数正好相等 B ．小于被排除在外地前定变量个数 C ．大于被排除在外地前定变量个数D ．以上三种情况都有可能发生 文档收集自网络，仅用于个人学习6) 简化式模型就是把结构式模型中地内生变量表示为 ( ).A. 外生变量和内生变量地函数关系B.前定变量和随机误差项地模型C.滞后变量和随机误差项地模型 D.外生变量和随机误差项地模量，也可以是 ( ).文档收集自网络，仅用于个人学习 A. 外生变量 B.滞后变量2)前定变量是 ( )地合称 .A.外生变量和滞后内生变量C.内生变量D. 外生变量和内生变量 C.外生变量和虚拟变量 D. 解释变量和被解释变量( ).A. 恰好识别B.不可识别 (4) 下面说法正确地是( ).A.内生变量是非随机变量 C.外生变量是随机变量 C.过度识别 D.不确定B. 前定变量是随机变量个人收集整理勿做商业用途型7) 对联立方程模型进行参数估计地方法可以分两类，即：( ).A.间接最小二乘法和系统估计方法B.单方程估计法和系统估计方法个人收集整理勿做商业用途C.单方程估计法和二阶段最小二乘法D.工具变量法和间接最小二乘法（8）在某个结构方程过度识别地条件下，不适用地估计方法是（）.A. 间接最小二乘法B.工具变量法C.二阶段最小二乘法D.有限信息极大似然估计法8.3行为方程和恒等式有什么区别？8.4如何确定模型中地外生变量和内生变量？8.5考虑下述模型：C t = α + β D t +u t I t = γ + δD t-1 + νt D t = C t +I t + Z t ；t=1 ，2，⋯，n其中 C = 消费支出，D= 收入，I = 投资，Z = 自发支出. C、I 和D是内生变量.试写出消费支出地简化型方程，并研究各方程地识别问题.8.6考虑下述模型：Y t = C t + I t +G t +X tC t = β 0 + β 1D t + β2C t-1 + u tD t = Y t –T tI t = α0 + α1Y t + α2R t-1 +νt 模型中各方程是正规化方程，u t、νt为扰动项.（1）请指出模型中地内生变量、外生变量和前定变量.（2）写出用2SLS法进行估计时，每个阶段中要估计地方程.8.7下面是一个简单地美国宏观经济模型（1960－1999）其中C=实际私人消费，I= 实际私人总投资，G=实际政府支出，Y ＝实际GDP，M= 当年价M2，R=长期利率；P＝消费价格指数.内生变量：C，I，R，Y 前定变量：C t-1，I t-1，M t-1，P t，R t-1 和G t.（1）应用识别地阶条件，决定各方程地识别状态；（2）你打算用什么方法来估计可识别行为方程？8.8假设有如下计量经济模型：其中，Y＝国民收入，I=净资本形成，C=个人消费，Q ＝利润，P=生活费用指数，R= 工业劳动生产率1）写出模型地内生变量、外生变量和前定变量；个人收集整理勿做商业用途（2）用识别地阶条件确定各方程地识别状态；（3）此模型中是否有可以用ILS 法估计地方程？如有，请指出；（4）写出用2SLS 法进行估计时，每个阶段中要估计地方程. 8.9考虑下述模型：消费方程：C t=α0 +α 1Y t +α2C t-1 +u①投资方程：I t=β0 +β1Y t +β2I t –1+u2t②进口方程：M t = 0 + 1Y t + u3t ③Y t = C t+ I t + G t + X t - M t模型中各方程是正规化方程，u 1t, ⋯u3t为扰动项.（1）请指出模型中地内生变量、外生变量和前定变量.（2）利用阶条件识别各行为方程.（3）写出用3SLS 进行估计时地步骤.8.10考察下述国民经济地简单模型式中，C为消费，Y 为国民收入，I 为投资，R为利率.设样本容量n 为20，已算得中间结果为：（1）判别模型中消费方程地识别状态；（2）用间接最小二乘法求消费方程结构式系数；（3）将采用哪种方法估计投资方程?为什么?（不必计算）8.11由联立方程模型；得到其简化式如下：（1）两结构方程可识别吗？（2）如果知道，识别情况有何变化？（3）若对简化式进行估计，结果如下：个人收集整理勿做商业用途试求出结构参数地值，并说明如何检验原假设个人收集整理勿做商业用途版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理。

第二章练习题及参考解答表中是1992年亚洲各国人均寿命（Y）、按购买力平价计算的人均GDP（X1）、成人识字率（X2）、一岁儿童疫苗接种率（X3）的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据（1）分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。

（2）对所建立的回归模型进行检验。

【练习题参考解答】（1）分别设定简单线性回归模型，分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系（2）对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.（3）分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年，全省生产总值为32000 亿元，比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为：（1）消费支出C的点预测值；（2）在95%的置信概率下消费支出C平均值的预测区间。

陈强高级计量经济学答案1、企业摊销自用的无形资产时，借记“管理费用”科目，贷记（）科目。

[单选题] *A.“投资收益”B.“累计摊销”(正确答案)C.“营业外收入”D.“无形资产”2、．（年浙江省高职考）下列项目中，不属于企业会计核算对象的经济活动是（）[单选题] *A购买设备B请购原材料(正确答案)C接受捐赠D利润分配3、．（年宁波二模考）下列关于会计主体的说法中，不正确的是（）[单选题] *A会计主体可以是独立法人，也可以是非法人B会计主体一定是法律主体(正确答案)C会计主体可以是一个企业，也可以是企业中的一个特定组成部分D会计主体有可能是单一企业，也可能是几个企业组成的企业集团4、对出租的无形资产进行摊销时，其摊销的价值应计入（）。

[单选题] *A.管理费用B.其他业务成本(正确答案)C.营业外支出D.销售费用5、销售费用不包括（）。

[单选题] *A.产品包装费B.公司经费(正确答案)C.广告费D.产品保险费6、．（年浙江省高职考）下列各项中，不属于经济业务的经济活动是（）[单选题] * A采购原材料并验收入库B生产产品领用原材料C支付职工工资D签订产品销售合同(正确答案)7、企业因自然灾害造成的损失，在扣除保险公司赔偿后应计入（）。

[单选题] *A.财务费用B.其他业务成本C.销售费用D.营业外支出(正确答案)8、企业在转销已经确认无法支付的应付账款时，应贷记的会计科目是（）。

[单选题] *A.其他业务收入B.营业外收入(正确答案)C.盈余公积D.资本公积9、企业用盈余公积转增资本时，转增后留存的盈余公积的数额不得少于转增前注册资本（）。

[单选题] *A.20％B.15％C.25％(正确答案)D.50％10、企业购入需要安装的固定资产，不论采用何种安装方式，固定资产的全部安装成本（包括固定资产买价以及包装运杂费和安装费）均应通过（）科目进行核算。

[单选题] *A.固定资产B.在建工程(正确答案)C.工程物资D.长期股权投资11、下列项目中，不属于职工薪酬的是（）。

中央财经大学高级计量经济学慕课答案
1、相关关系是指（）
A、变量间的非独立关系
B、变量间的因果关系
C、变量间的函数关系
D、变量间不确定性的依存关系
答案：变量间不确定性的依存关系
2、总体回归直线是解释变量取各给定值时被解释变量条件期望的轨迹。

答案：√
3、总体回归函数给出了对应于每一个自变量的因变量的值。

答案：错误
1、以下模型不是线性回归的是（）
答案：无异常值
2、线性回归是指解释变量和被解释变量之间呈现线性关系。

答案：错
1、若随机扰动项满足古典假定，以下说法错误的是（）
答案：B
2、假设线性回归模型满足全部基本假设，则其参数的估计量具备（）。

A、可靠性
B、线性性
C、无偏性
D、有效性
答案：线性性;
1、满足基本假设条件下，随机误差项服从正态分布，但被解释变量Y不一定服从正态分布。

答案：错误
2、任何两个计量经济模型的可决系数都是可以比较的。

答案：错
3、通过可决系数的高低可以进行显著性判断。

答案：×
1、计量经济预测的条件是（）
A、模型设定的关系式不变
B、所估计的参数不变
C、解释变量在预测期的取值已作出预测
D、没有对解释变量在预测期的取值进行过预测
答案：模型设定的关系式不变;
2、对被解释变量的预测可以分为（）
A、被解释变量平均值的点预测
B、被解释变量平均值的区间预测
C、被解释变量个别值的点预测
D、被解释变量个别值的区间预测
答案：被解释变量平均值的点预测;
3、预测区间的宽窄只与样本容量n有关。

答案：错。

计量经济学课后答案计量经济学课后答案第⼀章绪论（⼀）基本知识类题型 1-1．什么是计量经济学？1-2．简述当代计量经济学发展的动向。

1-3．计量经济学⽅法与⼀般经济数学⽅法有什么区别？1-4．为什么说计量经济学是经济理论、数学和经济统计学的结合？试述三者之关系。

1-5．为什么说计量经济学是⼀门经济学科？它在经济学科体系中的作⽤和地位是什么？ 1-6．计量经济学的研究的对象和内容是什么？计量经济学模型研究的经济关系有哪两个基本特征？1-7．试结合⼀个具体经济问题说明建⽴与应⽤计量经济学模型的主要步骤。

1-8．建⽴计量经济学模型的基本思想是什么？1-9．计量经济学模型主要有哪些应⽤领域？各⾃的原理是什么？1-10．试分别举出五个时间序列数据和横截⾯数据，并说明时间序列数据和横截⾯数据有和异同？1-11．试解释单⽅程模型和联⽴⽅程模型的概念，并举例说明两者之间的联系与区别。

1-12．模型的检验包括⼏个⽅⾯？其具体含义是什么？ 1-13．常⽤的样本数据有哪些？1-14．计量经济模型中为何要包括随机误差项？简述随机误差项形成的原因。

1-15．估计量和估计值有何区别？哪些类型的关系式不存在估计问题？ 1-16．经济数据在计量经济分析中的作⽤是什么？1-17．下列假想模型是否属于揭⽰因果关系的计量经济学模型？为什么？⑴其中为第t 年农村居民储蓄增加额（亿元）、为第t 年城镇居民可⽀配收⼊总额（亿元）。

⑵其中为第（1 t ）年底农村居民储蓄余额（亿元）、为第t 年农村居民纯收⼊总额（亿元）。

1-18．指出下列假想模型中的错误，并说明理由：（1）其中，为第t 年社会消费品零售总额（亿元），为第t 年居民收⼊总额（亿元）（城镇居民可⽀配收⼊总额与农村居民纯收⼊总额之和），为第t 年全社会固定资产投资总额（亿元）。

（2）t t Y C 2.1180+=其中，C 、Y 分别是城镇居民消费⽀出和可⽀配收⼊。

（3）t t t L K Y ln 28.0ln 62.115.1ln -+=其中，Y 、K 、L 分别是⼯业总产值、⼯业⽣产资⾦和职⼯⼈数。

1.3 某市居民家庭人均年收入服从4000X =元，1200σ=元的正态分布，求该市居民家庭人均年收入：（1）在5000—7000元之间的概率；（2）超过8000元的概率；（3）低于3000元的概率。

（1）()()()()()2,0,15000700050007000()2.50.835( 2.5)62X N X X XN XX XXP X P F F X XP σσσσσσ-∴---∴<<=<<--=<<=根据附表1可知 ()0.830.5935F =，()2.50.9876F =()0.98760.5935500070000.19712P X -∴<<==PS ：()()5000700050007000()55( 2.5) 2.5660.99380.79760.1961XX XXP X P X X P σσσσ---<<=<<-⎛⎫=<<=Φ-Φ ⎪⎝⎭=-=在附表1中，()()F Z P x xz σ=-<（2）()80001080003X X X X X P X P P σσσ⎛⎫⎛⎫--->=>=> ⎪⎪⎝⎭⎝⎭=0.0004 （3）()3000530006X X X X X P X P P σσσ⎛⎫⎛⎫---<=<=<- ⎪ ⎪⎝⎭⎝⎭=0.2023 ()030001050300036X X X X X X P X P P σσσσ⎛⎫⎛⎫----<<=<<=-<<- ⎪ ⎪⎝⎭⎝⎭=0.2023-0.0004=0.20191.4 据统计70岁的老人在5年内正常死亡概率为0.98，因事故死亡的概率为0.02。

保险公司开办老人事故死亡保险，参加者需缴纳保险费100元。

若5年内因事故死亡，公司要赔偿a 元。

应如何测算出a ，才能使公司可期望获益；若有1000人投保，公司可期望总获益多少？设公司从一个投保者得到的收益为X ，则则()1000.02E X a =-故要是公司可期望获益，则有()1000.02E X a =->0，即5000a <PS ：赔偿金应大于保险费？1000人投保时，公司的期望总收益为()10001000.021*******a a -=-2.1 写出过原点的一元、二元线性回归模型，并分别求出回归系数的最小二乘估计。

1.3 某市居民家庭人均年收入服从4000X =元，1200σ=元的正态分布，求该市居民家庭人均年收入：（1）在5000—7000元之间的概率；（2）超过8000元的概率；（3）低于3000元的概率。

（1）根据附表1可知()0.830.5935F =，()2.50.9876F = PS ：在附表1中，()()F Z P x xz σ=-<（2）()80001080003X X X X X P X P P σσσ⎛⎫⎛⎫--->=>=> ⎪⎪⎝⎭⎝⎭=0.0004 （3）()3000530006X X X X X P X P P σσσ⎛⎫⎛⎫---<=<=<- ⎪ ⎪⎝⎭⎝⎭=0.2023 =0.2023-0.0004=0.20191.4 据统计70岁的老人在5年内正常死亡概率为0.98，因事故死亡的概率为0.02。

保险公司开办老人事故死亡保险，参加者需缴纳保险费100元。

若5年内因事故死亡，公司要赔偿a 元。

应如何测算出a ，才能使公司可期望获益；若有1000人投保，公司可期望总获益多少？设公司从一个投保者得到的收益为X ，则则()1000.02E X a =-故要是公司可期望获益，则有()1000.02E X a =->0，即5000a <PS ：赔偿金应大于保险费？1000人投保时，公司的期望总收益为()10001000.021*******a a -=-2.1 写出过原点的一元、二元线性回归模型，并分别求出回归系数的最小二乘估计。

解答：过原点的一元线性回归模型为Y X βε=+ 约束最小二乘估计：y x αβε=++过原点的二元线性回归模型为1122Y X X ββε=++ 2.2针对多元线性回归模型试证明经典线性回归模型参数OLS 估计量的性质()ˆE ββ=和()()12ˆˆ,Cov X X ββσ-'=，并说明你在证明时用到了哪些基本假定。

1.研究宁波市财政预算收入与该市国内生产总值的关系。

采用时间序列数据资料（1978—2004年），（1）建立宁波市财政预算收入对该市国内生产总值的线性回归模型。

（2）使用普通最小二乘法对模型作出估计。

（3）根据回归结果对总体回归模型进行检验。

（4）若2006年该市的国内生产总值为2864.49亿元，试给出该市2006年财政收入的预测值和置信度为95%的预测区间，并与实际发生值（466.5亿元）进行比较。

（1）作宁波市财政预算收入Y（亿元）与该市国内生产总值X（亿元）的散点图。

从散点图可以看出Y与X大体呈线性关系，所以建立的计量经济模型为以下线性模型Y=β1+β2X+u其中β1、β2为估计参数，u表示随机误差项。

(2) 利用EViews软件，输入Y、X等数据，采用这些数据对模型进行OLS回归，回归结果如下在本例中参数估计有以下结果。

Y^i=-9.452819+0.144417Xi(6.924101) (0.008581)t=(-1.3652) (16.8293)r2=0.9189 F=283.2261 df=25回归结果图形：（3）模型检验经济意义检验：所估计参数β2=0.144417，说明宁波市国内生产总值每增加一亿元，该市财政预算收入增加0.144417亿元。

符合财政预算收入随gdp增加而增加的经济学意义。

拟合优度检验：在本例中可决系数为0.9189，说明所建模型整体上对样本数据你和较好，即解释变量“宁波市国内生产总值”对被解释变量“该市财政预算收入”的绝大部分差异做出了解释。

对回归系数的t检验：分别针对H0 : β（j） = 0 (j = 1、2) 给定显著性水平α= 0.05，在t分布表中查出自由度为n-k = 25的临界值t α/2 (n-k) = 2.060。

由表中数据可得，与β1、β2的估计值对应的t统计量分别为-1.3652、16.8293。

t(β1)的绝对值小于t α /2 (n-k) = 2.060 ，t(β2)的绝对值大于t α /2 (n-k) = 2.060。